[Day 57] 區塊鏈與人工智能的聯動應用:理論、技術與實踐
區塊鏈的零知識證明技術
一、引言
隨著區塊鏈技術的不斷發展,如何在保護用戶隱私的同時確保數據的完整性和可信度成為了研究的焦點。零知識證明(Zero-Knowledge Proof,ZKP)技術就是其中的一項關鍵技術,它允許一方在不洩露任何額外信息的情況下,向另一方證明其擁有某種知識或信息。本文將深入探討零知識證明技術的基本原理、在區塊鏈中的應用場景,並通過實際代碼示例演示如何實現零知識證明。
二、零知識證明的基本概念
1. 零知識證明的定義
零知識證明是一種密碼學技術,允許證明者(Prover)在不洩露任何其他信息的情況下向驗證者(Verifier)證明某個聲明是真實的。這一過程必須滿足以下三個特性:
- 完備性:如果聲明是真實的,誠實的驗證者會被說服。
- 正直性:如果聲明是虛假的,誠實的驗證者不會被說服。
- 零知識性:除非驗證者已經知道聲明的內容,否則他無法從證明過程中學到任何額外的信息。
2. 零知識證明的歷史背景
零知識證明技術最早由Goldwasser、Micali和Rackoff於1985年提出,他們首次提出了一個基於數學難題的互動式證明系統。隨著時間的推移,這一技術被逐步應用到各種場景中,尤其是在區塊鏈領域。
三、零知識證明技術的工作原理
1. 基於代數結構的零知識證明
零知識證明的核心思想是利用代數結構,尤其是模運算中的離散對數問題(Discrete Logarithm Problem, DLP),來構建證明。例如,證明者可以證明其知道一個值 xxx 使得 y=gxmod py = g^x \mod py=gxmodp,但不直接透露 xxx 的具體值。
2. 交互式零知識證明
在交互式零知識證明中,證明者和驗證者之間會進行多輪的互動。每一輪互動中,證明者會向驗證者展示一部分信息,驗證者則會提出挑戰,最後驗證者根據所有信息判斷證明是否成立。
3. 非交互式零知識證明
非交互式零知識證明(Non-Interactive Zero-Knowledge, NIZK)是一種特殊的零知識證明形式,該技術在區塊鏈中尤為重要。它允許證明者通過單一訊息向驗證者展示其證明,這使得它非常適合區塊鏈這種無需交互的分布式系統。
四、零知識證明在區塊鏈中的應用
1. 匿名交易
零知識證明在區塊鏈中的最典型應用之一就是匿名交易。Zcash就是一個採用了零知識證明技術的加密貨幣,它利用了名為zk-SNARKs(零知識簡潔非交互式知識論證)的技術來隱藏交易的詳細信息。
2. 隱私保護
零知識證明技術能夠在保證隱私的前提下驗證交易,這使得區塊鏈上的數據隱私保護變得更加可行。許多基於區塊鏈的身份驗證系統也採用了零知識證明技術,以確保用戶的隱私不會被洩露。
3. 智能合約驗證
智能合約中的數據通常需要驗證其真實性,但不一定需要洩露具體內容。零知識證明技術可以用來在不洩露合約具體執行邏輯的情況下,證明其正確性。
五、零知識證明技術的實際代碼示例
1. 簡單的零知識證明實現
以下是一個簡單的零知識證明代碼示例,用於證明某人知道一個數字的平方根。
import random# 設置公共參數
p = 23 # 大質數
g = 5 # 基數# 設置秘密值
x = 4 # 我們知道的秘密數字
y = pow(g, x, p) # 計算 y = g^x mod p# 證明階段
r = random.randint(1, p-1) # 生成隨機數 r
t = pow(g, r, p) # 計算 t = g^r mod p# 模擬驗證者的挑戰
challenge = random.randint(0, 1) # 驗證者選擇 0 或 1# 證明者計算響應
if challenge == 0:response = r
else:response = (r + x) % (p-1)# 驗證者檢查證明
if challenge == 0:assert pow(g, response, p) == t
else:assert pow(g, response, p) == (t * y) % pprint("證明成功!")
代碼解釋
- 公共參數設置:我們選擇了一個大質數 ppp 和一個基數 ggg,這些都是公開的信息。
- 秘密值:我們設置了一個秘密值 xxx,並計算 y=gxmod py = g^x \mod py=gxmodp,這是我們需要證明的值。
- 證明階段:證明者生成一個隨機數 rrr 並計算 t=grmod pt = g^r \mod pt=grmodp。
- 驗證者的挑戰:驗證者隨機選擇 0 或 1,作為對證明者的挑戰。
- 證明者的響應:根據挑戰值的不同,證明者計算不同的響應值 responseresponseresponse。
- 驗證者的驗證:驗證者根據響應值檢查證明是否成立。
2. zk-SNARKs 的簡單實現示例
以下是一個基於 zk-SNARKs 的簡單例子,用於展示零知識證明在更複雜場景中的應用。這裡使用 pycryptodome 庫來實現一個簡單的 zk-SNARKs 例子。
from pycryptodome.PublicKey import RSA
from pycryptodome.Signature import pkcs1_15
from pycryptodome.Hash import SHA256# 設置 RSA 密鑰對
key = RSA.generate(2048)
public_key = key.publickey()# 設置秘密值和公共參數
secret_value = b'zkp secret'
h = SHA256.new(secret_value)# 證明者生成證明
signature = pkcs1_15.new(key).sign(h)# 驗證者驗證證明
try:pkcs1_15.new(public_key).verify(h, signature)print("證明成功,驗證通過!")
except (ValueError, TypeError):print("證明失敗,驗證不通過!")
代碼解釋
- 密鑰對生成:我們生成了一對 RSA 密鑰,用於後續的簽名和驗證。
- 秘密值設置:證明者設定了一個秘密值
secret_value,並使用 SHA-256 哈希算法計算其哈希值。 - 證明生成:證明者使用 RSA 私鑰對哈希值進行簽名,生成證明。
- 驗證證明:驗證者使用 RSA 公鑰對證明進行驗證,如果證明有效,則驗證通過。
3. zk-SNARKs 在區塊鏈中的應用示例
在區塊鏈中,zk-SNARKs 被用於構建匿名交易。以下是一個基於 zk-SNARKs 構建匿名交易的示例代碼,使用 libsnark 庫來演示 zk-SNARKs 的實現。
#include <libsnark/common/default_types/r1cs_ppzksnark_pp.hpp>
#include <libsnark/zk_proof_systems/ppzksnark/r1cs_ppzksnark/examples/run_r1cs_ppzksnark.hpp>using namespace libsnark;int main() {// 初始化 SNARK 的參數default_r1cs_ppzksnark_pp::init_public_params();// 構建一個簡單的 R1CS 約束系統r1cs_example<libff::Fr<default_r1cs_ppzksnark_pp>> example = generate_r1cs_example_with_field_input<libff::Fr<default_r1cs_ppzksnark_pp>>(100, 10);// 執行鍵生成、證明生成和驗證const r1cs_ppzksnark_keypair<default_r1cs_ppzksnark_pp> keypair = generate_r1cs_ppzksnark_keypair<default_r1cs_ppzksnark_pp>(example.constraint_system);const r1cs_ppzksnark_proof<default_r1cs_ppzksnark_pp> proof = generate_r1cs_ppzksnark_proof(keypair.pk, example.primary_input, example.auxiliary_input);const bool verification = verify_r1cs_ppzksnark_proof(keypair.vk, example.primary_input, proof);std::cout << "SNARK 證明驗證結果: " << verification << std::endl;return 0;
}
代碼解釋
- 初始化參數:首先初始化 zk-SNARKs 的公共參數。
- 構建約束系統:生成一個 R1CS(Rank-1 Constraint System),它是 zk-SNARKs 中的基本數學表示,用於表示需要證明的命題。
- 鍵生成與證明生成:根據約束系統生成一對密鑰(包括證明鍵和驗證鍵),並使用證明鍵生成證明。
- 驗證證明:使用驗證鍵來驗證生成的證明,並輸出驗證結果。
六、零知識證明技術的優點與挑戰
1. 優點
- 隱私保護:零知識證明允許在不洩露敏感信息的情況下進行驗證,非常適合需要高隱私保護的場景。
- 安全性:基於數學難題的零知識證明具有極高的安全性,難以破解。
- 靈活性:零知識證明技術可以應用於多種場景,如身份驗證、智能合約、隱私交易等。
2. 挑戰
- 計算複雜度:零知識證明的計算量通常較大,可能影響系統的性能。
- 實施成本:由於技術的複雜性,零知識證明的實施成本較高,需要專業的技術支持。
- 標準化:目前零知識證明技術尚未完全標準化,不同平台之間的兼容性可能存在問題。
七、結論
零知識證明技術在區塊鏈領域具有廣泛的應用前景,特別是在保護用戶隱私和數據安全方面具有不可替代的作用。隨著技術的不斷進步,零知識證明的應用將更加廣泛,並且可能成為未來區塊鏈技術發展的重要方向之一。
相关文章:

[Day 57] 區塊鏈與人工智能的聯動應用:理論、技術與實踐
區塊鏈的零知識證明技術 一、引言 隨著區塊鏈技術的不斷發展,如何在保護用戶隱私的同時確保數據的完整性和可信度成為了研究的焦點。零知識證明(Zero-Knowledge Proof,ZKP)技術就是其中的一項關鍵技術,它允許一方在不…...

06结构型设计模式——代理模式
一、代理模式简介 代理模式(Proxy Pattern)是一种结构型设计模式(GoF书中解释结构型设计模式:一种用来处理类或对象、模块的组合关系的模式),代理模式是其中的一种,它可以为其他对象提供一种代…...

《深入浅出多模态》(九)多模态经典模型:MiniGPT-v2、MiniGPT5
🎉AI学习星球推荐: GoAI的学习社区 知识星球是一个致力于提供《机器学习 | 深度学习 | CV | NLP | 大模型 | 多模态 | AIGC 》各个最新AI方向综述、论文等成体系的学习资料,配有全面而有深度的专栏内容,包括不限于 前沿论文解读、资料共享、行业最新动态以、实践教程、求职…...

调试和优化大型深度学习模型 - 0 技术介绍
调试和优化大型深度学习模型 - 0 技术介绍 flyfish LLaMA Factory LLaMA Factory 是一个简单易用且高效的大型语言模型(Large Language Model)训练与微调平台。通过 LLaMA Factory,可以在无需编写任何代码的前提下,在本地完成上…...

华为S3700交换机配置VLAN的方法
1.VLAN的详细介绍 VLAN(Virtual Local Area Network)即虚拟局域网,是一种将一个物理的局域网在逻辑上划分成多个广播域的技术。 1.1基本概念 1)作用: 隔离广播域:通过将网络划分为不同的 VLAN,广播帧只会在同一 VLAN 内传播,而不会扩散到其他 VLAN 中,从而有效…...
:深入详解C++网络编程:套接字(Socket)开发技术)
学懂C++(三十八):深入详解C++网络编程:套接字(Socket)开发技术
目录 一、概述与基础概念 1.1 套接字(Socket)概念 1.2 底层原理与网络协议 1.2.1 网络协议 1.2.2 套接字工作原理 二、C套接字编程核心技术 2.1 套接字编程的基本步骤 2.2 套接字编程详细实现 2.2.1 创建套接字 2.2.2 绑定地址 2.2.3 监听和接…...

SpringBoot-配置加载顺序
目录 前言 样例 内部配置加载顺序 样例 小结 前言 我之前写的配置文件,都是放在resources文件夹,根据当前目录下,优先级的高低,判断谁先被加载。但实际开发中,我们写的配置文件并不是,都放…...

第八周:机器学习笔记
第八周机器学习笔记 摘要Abstract机器学习1. 鱼和熊掌和可兼得的机器学习1.1 Deep network v.s. Fat network 2. 为什么用来验证集结果还是不好? Pytorch学习1. 卷积层代码实战2. 最大池化层代码实战3. 非线性激活层代码实战 总结 摘要 本周学习对李宏毅机器学习视…...

音乐怎么剪切掉一部分?5个方法,轻松学会音频分割!(2024全新)
音乐怎么剪切掉一部分?音频文件是娱乐和创作的重要基础。音频在我们日常生活中发挥着重要作用,从音乐播放列表到有趣的视频,它无处不在。无论是音乐爱好者还是内容创作者,我们常常需要对音频文件进行剪切和编辑。想象一下…...

洛谷 CF295D Greg and Caves
题目来源于:洛谷 题目本质:动态规划dp,枚举 解题思路:将整个洞分成两半,一半递增,一半递减。我们分别 DP 求值,最后合并。状态转移方程为:dpi,jk2∑j(j−k1)dpi−1,k1。枚举极…...

【图像处理】在图像处理算法开发中,有哪些常见的主观评价指标和客观评价指标?
主观评价指标 在图像处理算法开发中,主观评价指标依赖于观察者的个人感受和判断,通常用于评估图像的视觉质量。以下是一些常见的主观评价指标: 平均意见分数 (Mean Opinion Score, MOS):通过收集多个评价者的评分并计算平均值来评…...

从零开始学cv-6:图像的灰度变换
文章目录 一,简介:二、图像的线性变换三、分段线性变换四,非线性变换4.1 对数变换4.2 Gamma变换 五,效果: 一,简介: 图像灰度变换涉及对图像中每个像素的灰度值执行数学运算,进而调整图像的视觉…...
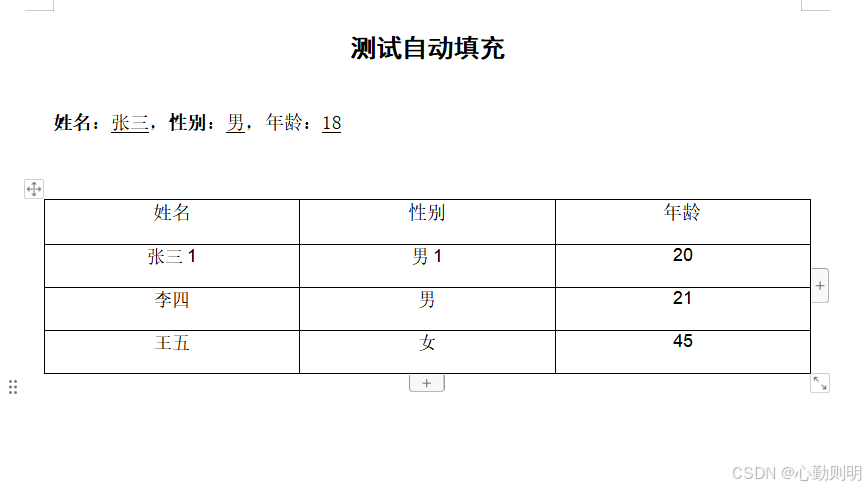
使用Apache POI和POI-OOXML实现word模板文档自动填充功能
最近接到一个新的需求,用户创建好模板文件保存到模板库,然后使用在线文档编辑器打开模板时,将系统数据填充到模板文件并生成新的word文件,然后在线编辑,研究使用Apache POI和POI-OOXML实现了这个功能。 Maven依赖 <…...

【HarmonyOS NEXT星河版开发学习】综合测试案例-各平台评论部分
目录 前言 功能展示 整体页面布局 最新和最热 写评论 点赞功能 界面构建 初始数据的准备 列表项部分的渲染 底部区域 index部分 知识点概述 List组件 List组件简介 ListItem组件详解 ListItemGroup组件介绍 ForEach循环渲染 列表分割线设置 列表排列方向设…...

垂直行业数字化表现抢眼 亚信科技全年利润展望乐观
大数据产业创新服务媒体 ——聚焦数据 改变商业 2024年8月14日,亚信科技控股有限公司(股票代码:01675.HK)公布了公司截至2024年6月30日的中期业绩。 财报数据显示,2024年上半年,亚信科技的营业收入为人民币…...

EmguCV学习笔记 VB.Net 4.1 颜色变换
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 教程VB.net版本请访问:EmguCV学习笔记 VB.Net 目录-CSDN博客 教程C#版本请访问:EmguCV学习笔记 C# 目录-CSD…...

【MySQL进阶之路】表结构的操作
目录 创建表 查看表 查看数据库有哪些表 查看表结构 查看表的详细信息 修改表 表的重命名 添加一列 修改某一列的属性 删除某一列 对列进行重命名 删除表 个人主页:东洛的克莱斯韦克-CSDN博客 【MySQL进阶之路】MySQL基础——从零认识MySQL-CSDN博客 创…...
3分钟搞定PDF转PPT!你一定要知道的3款转换神器!
在数字办公成为主流的当下,我们每天会收到各类基于数字化方式存储的办公文档,如PDF、PPT、Word、Excel文档等。 日常处理这些文档时,经常需要在不同格式的文档之间进行切换和转换,其中将PDF转换为PPT就是一个非常高频的需求&…...

【EasyExcel】导出excel-设置动态表头并导出数据
需求背景: 导出excel的设置某些表头动态导出(可以根据筛选条件或一些属性的数据量),方便导出后用户查看想看的信息。 一、技术选型: easyExcel的原生数据处理 二、方案设计: 根据EasyExcel支持的表头List<List<String>…...

深入探索 Elasticsearch 8:新特性与核心原理剖析(上)
深入探索 Elasticsearch 8:新特性与核心原理剖析 目录 一、引言 (二)版本 8 的重要意义 二、Elasticsearch 8 的新特性 三、Elasticsearch 的核心原理 一、引言 (一)Elasticsearch 简介 在大数据处理和搜索领域…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
