leetcode每日一题:134. 加油站
系列:贪心算法
语言:java
题目来源:Leetcode134. 加油站
题目
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。
示例 2:
输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
因此,无论怎样,你都不可能绕环路行驶一周。
约束条件:
gas.length == n
cost.length == n
1 <= n <= 105
0 <= gas[i], cost[i] <= 104
思路:
分析:拿到这道题我们首先可以分析出,如果车子想跑一圈,题中所给的油量数组和必须大于等于消耗油量的和,相当于做了一步剪枝操作。(不过调用这个内置函数好像更慢了哈哈)
if(Arrays.stream(gas).sum()<Arrays.stream(cost).sum()){return -1;}
如果只是空看两个数组分析不太直观,可以直接让两个数组求差,放在一个数组里来进行分析.
例如题中给的案例: gas = [1,2,3,4,5], cost = [3,4,5,1,2],求差后nums = [-2,-2,-2,3,3].,此时我们通过一个for循环来对nums数组进行求和,同时用一个最小值mix来记录求和过程中的最小值
int sum =0;int mix = Integer.MAX_VALUE;int length = gas.length;int nums[] = new int[length];for(int i =0;i<length;i++){nums[i] = gas[i]-cost[i];sum+=nums[i];if(mix>sum){mix = sum;}}
此时mix已经记录下来这个过程中最小值,同时我们也拿到了油数sum之后,然后就会出现三种情况。
情况1:如果sum<0,我们开头已经做过剪枝操作了,所以这一种情况已经被排除了
情况2:在sum>0情况下,出现mix>=0,则说明从0开始的话,遍历一遍过程中油量始终大于消耗的油量,所以从第一个加油站出发就满足条件,所以return 0;
if(mix>=0){return 0;}
难点:情况3:在sum>0情况下,同时mix<0,(假设这个位置是m)说明出现了油量从0-m过程中有油量总和小于消耗量且是相差最大的时刻,此时我们可以反向遍历,相当于倒着求和,直到mix大于等于0时(假如这个位置是n,你可能会想从m-n这一块区间如果和为负数怎么办,哈哈那是不可能的,因为首先总油量和大于消耗的油量,然后如果m-n这个区间油量为负数,那么那个最小值mix的下标就应该在m之后了,也会向后移动,所以m-n这个区间的值必定为0或者整数哈哈)。这里比较难理解,建议看个十几遍。
for(int i =length-1;i>=0;i--){mix +=nums[i];if(mix>=0){return i;}}
完整代码:
class Solution {public int canCompleteCircuit(int[] gas, int[] cost) {if(Arrays.stream(gas).sum()<Arrays.stream(cost).sum()){return -1;}int sum =0;int mix = Integer.MAX_VALUE;int length = gas.length;int nums[] = new int[length];for(int i =0;i<length;i++){nums[i] = gas[i]-cost[i];sum+=nums[i];if(mix>sum){mix = sum;}} if(mix>=0){return 0;}for(int i =length-1;i>=0;i--){mix +=nums[i];if(mix>=0){return i;}}return -1;}
}
感谢您的阅读,希望对您有所帮助。关注我,完成每日算法自律打卡,什么时候开始都不晚!!
相关文章:

leetcode每日一题:134. 加油站
系列:贪心算法 语言:java 题目来源:Leetcode134. 加油站 题目 在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。 你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i1 个加油站需要消耗汽油 cost[…...

开放式基金实时排行 API 数据接口
开放式基金实时排行 API 数据接口 多维度参数返回,实时数据,类型参数筛选。 1. 产品功能 返回实时开放式基金排行数据可定义查询基金类型参数;多个基金属性值返回多维指标,一次查询毫秒级返回;数据持续更新与维护&am…...

Android开发中synchronized的实现原理
synchronized的三种使用方式 **1.修饰实例方法,**作用于当前实例加锁,进入同步代码前要获得当前实例的锁。 没有问题的写法: public class AccountingSync implements Runnable{//共享资源(临界资源)static int i0;/*** synchronized 修饰实例方法*/p…...
)
【华为OD机试 2023最新 】 统一限载货物数最小值(C++)
题目描述 火车站附近的货物中转站负责将到站货物运往仓库,小明在中转站负责调度2K辆中转车(K辆干货中转车,K辆湿货中转车)。 货物由不同供货商从各地发来,各地的货物是依次进站,然后小明按照卸货顺序依次装货到中转车,一个供货商的货只能装到一辆车上,不能拆装,但是…...
【生活工作经验 十】ChatGPT模型对话初探
最近探索了下全球大火的ChatGPT,想对此做个初步了解 一篇博客 当今社会,自然语言处理技术得到了迅速的发展,人工智能技术也越来越受到关注。其中,基于深度学习的大型语言模型,如GPT(Generative Pre-train…...

基于Spring Boot房产销售平台的设计与实现【源码+论文】分享
开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包:Maven3.3.9 摘要 信息技术的发展…...

不同类型的电机的工作原理和控制方法汇总
电机控制是指对电机的启动、调速(加速、减速)、运转方向和停止进行的控制,不同类型的电机有着不同的工作原理和控制方法。 一、无刷电机 无刷电机是由电机主体和电机驱动板组成的一种没有电刷和换向器的机电一体化产品。在无刷电机中…...

计算机网络管理 TCP三次握手的建立过程,Wireshark抓包分析并验证TCP三次握手建立连接的报文
⬜⬜⬜ ---🟧🟨🟩🟦🟪 (*^▽^*)欢迎光临 🟧🟨🟩🟦🟪---⬜⬜⬜ ✏️write in front✏️ 📝个人主页:陈丹宇jmu 🎁欢迎各位→…...
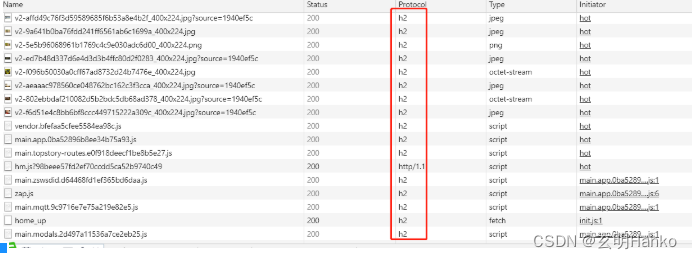
HTTP/2.x:最新的网页加载技术,快速提高您的SEO排名
2.1 http2概念HTTP/2.0(又称HTTP2)是HTTP协议的第二个版本。它是对HTTP/1.x的更新,旨在提高网络性能和安全性。HTTP/2.0是由互联网工程任务组(IETF)标准化的,并于2015年发布。2.2 http2.x与http1.x区别HTTP…...

机器学习----线性回归
第一关:简单线性回归与多元线性回归 1、下面属于多元线性回归的是? A、 求得正方形面积与对角线之间的关系。 B、 建立股票价格与成交量、换手率等因素之间的线性关系。 C、 建立西瓜价格与西瓜大小、西瓜产地、甜度等因素之间的线性关系。 D、 建立西瓜…...
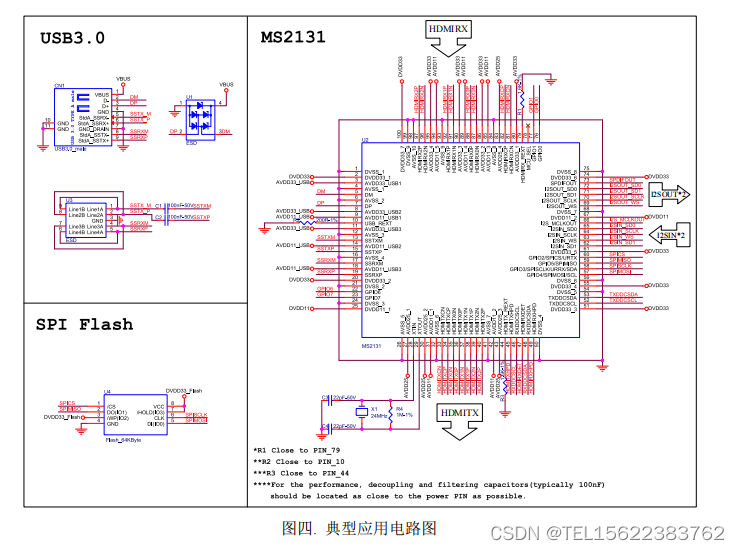
MS2131 USB 3.0 高清音视频采集+HDMI 环出+混音处理芯片 应用网络直播一体机
MS2131 是一款 USB 3.0 高清视频和音频采集处理芯片,内部集成 USB 3.0 Device 控制器、 数据收发模块、音视频处理模块。MS2131 可以通过 USB 3.0 接口将 HDMI 输入的音视频信号传 送到 PC、智能手机、平板电脑上预览或采集。MS2131 支持 HDMI 环出功能,…...

基于堆与AdjustDown的TOP-K问题
TIPSTOP-K问题TOP-K问题:就是说现在比如说有n个数据,然后需要从这n个数据里面找到最大的或最小的前k个。一般来讲思路的话就是:先把这n个数据给他建一个堆,建堆完成之后,然后就去调堆,然后大概只需要调k次&…...
在CentOS上安装Docker引擎
1,先决条件#### 1-1操作系统要求1-2 卸载旧版本 2,安装方法2-1使用存储库安装设置存储库安装 Docker 引擎 本文永久更新地址: 官方地址:https://docs.docker.com/engine/install/centos/ 1,先决条件 #### 1-1操作系统要求 要安装 Docker Engine,您需要…...

【10】核心易中期刊推荐——模式识别与机器学习
🚀🚀🚀NEW!!!核心易中期刊推荐栏目来啦 ~ 📚🍀 核心期刊在国内的应用范围非常广,核心期刊发表论文是国内很多作者晋升的硬性要求,并且在国内属于顶尖论文发表,具有很高的学术价值。在中文核心目录体系中,权威代表有CSSCI、CSCD和北大核心。其中,中文期刊的数…...

【数据结构】并查集
目录 一:用途 二:实现 O(1) 三:例题 例题1:集合 例题2:连通图无向 例题3:acwing 240 食物链 一:用途 将两个集合合并询问两个元素是否在一个集合当中 二:实现 O(1) 每…...

软考--网络攻击分类
网络攻击的主要手段包括口令入侵、放置特洛伊木马程序、拒绝服务(DoS)攻击、端口扫描、网络监听、欺骗攻击和电子邮件攻击等。口令入侵是指使用某些合法用户的账号和口令登录到目的主机,然后再实施攻击活动。特洛伊木马(Trojans)程序常被伪装…...

蓝桥杯刷题冲刺 | 倒计时17天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.长草2.分考场1.长草 题目 链接: 长草 - 蓝桥云课 (lanqiao.cn) 题目描述 小明有一…...

冲击蓝桥杯-并查集,前缀和,字符串
目录 前言 一、并查集 1、并查集的合并(带路径压缩) 2、询问是否为同一个集合 3、例题 二、前缀和 1 、前缀和是什么 2、经典题目 三- 字符串处理 1、字符串的插入 2、字符串转化为int类型 3、字符反转 前言 并查集合前缀,字符串…...

【matlab学习笔记】线性方程组求解方法
线性方程组求解方法2.1 求逆法实现方式例子2.2 分解法LU分解(Doolittle分解)实现方法例子QR分解法实现方法例子Cholesky 分解法实现方法例子奇异值分解法实现方法例子Hessenberg 分解实现方法例子Schur 分解实现方法例子2.3 迭代法逐次迭代法里查森迭代法…...

Python带你一键下载到最新章节,不付费也能看
前言 大家早好、午好、晚好吖 ❤ ~欢迎光临本文章 完整源码、素材皆可点击文章下方名片获取此处跳转 开发环境: python 3.8 运行代码 pycharm 2022.3 辅助敲代码 requests 发送请求/第三方模块 模块安装:win R 输入cmd 输入安装命令 pip install 模块名 如果…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

拟合问题处理
在机器学习中,核心任务通常围绕模型训练和性能提升展开,但你提到的 “优化训练数据解决过拟合” 和 “提升泛化性能解决欠拟合” 需要结合更准确的概念进行梳理。以下是对机器学习核心任务的系统复习和修正: 一、机器学习的核心任务框架 机…...
