当前位置： 首页 > news >正文

vue3 cascader省市区三级联动如何指定字段，如何根据id查到对应的名字

news 2025/9/19 0:11:09 
如果我们接口数据字段名不是value和code。要加个props
:props="{ value:'code',label:'regionName'}"根据id查name需要一个ref和一个@change事件<el-cascader :options="areaData" ref="addressCodeRef" @change="handleChange" :props="{ value:'code',label:'regionName'}" placeholder="请选择机构所在地"  v-model="addressCode" clearable style="width:100%" />
const  addressCodeRef=ref();
const handleChange = ()=> {console.log("label====",addressCodeRef.value.getCheckedNodes()[0])
}

打印的内容如下

相关文章：

vue3 cascader省市区三级联动如何指定字段，如何根据id查到对应的名字

如果我们接口数据字段名不是value和code。要加个props :props"{ value:code,label:regionName}"根据id查name需要一个ref和一个change事件<el-cascader :options"areaData" ref"addressCodeRef" change"handleChange" :props"…...

编程日记 2024/8/21 3:57:55

算法4：前缀和（上）

文章目录 一维前缀和二维前缀和寻找数组的中心下标除自身以外数组的乘积 一维前缀和 二维前缀和 寻找数组的中心下标 class Solution { public:int pivotIndex(vector<int>& nums) {int n nums.size();vector<int> f(n), g(n);f[0] nums[0];g[n - 1] num…...

编程日记 2024/8/21 3:56:54

美国政府紧急应对三星Galaxy手机安全漏洞

一、美国政府紧急通知更新三星Galaxy手机系统 美国政府近日发布紧急通知&#xff0c;要求联邦政府雇员在8月28日前更新三星Galaxy手机系统&#xff0c;否则将面临禁止使用这些设备的后果。这是继7月针对Pixel手机用户的类似要求之后的又一次紧急行动。此次事件的导火索是谷歌发…...

编程日记 2024/8/21 3:55:53

看 逆行人生

电影和我的职业本身有相关性&#xff0c;而且我特别喜欢徐峥执导的电影&#xff0c;这次的题材也算是碰上自己的胃口。 周六&#xff0c;下了大半天的雨&#xff0c;早上驱车到公司加班&#xff0c;下午六点多到时候特别想去看电影&#xff0c;果断再驱车从公司赶回来&#xff…...

编程日记 2024/8/21 3:54:52

0819、0820梳理及一些面试题梳理

一、抓包分析 二、HTTP服务器 三、动态库与静态库 四、一些面试题 指针数组和数组指针的区别&#xff1a;指针数组本质是一个数组&#xff0c;只是数组中存储的是指针变量。数组指针存储的是该数组的起始地址&#xff0c;对该指针来说每偏移一个单位就是偏移了一整个数组的地…...

编程日记 2024/8/21 3:52:50

HttpUtils工具类（一）常见的HttpUtils工具类及如何自定义java的http连接池

目录 一、几种常见的Http调用方式 1. 使用 Apache HttpClient 2. 使用 OKhttpClient 3. 使用第三方库&#xff08;Hutool&#xff09;的http链接池 4. 使用 Spring RestTemplate 5. 使用 Java 原生的HttpURLConnection 二、总结 常用三种HttpUtils对比总结 一、几种常见…...

编程日记 2024/8/21 3:50:48

使用 Lombok 遇到一个问题

起因是换了一个电脑&#xff0c;重新从服务器上拉了一个项目。项目是由maven构建的&#xff0c;在控制台中使用mvn命令编译项目时&#xff0c;没有任何问题&#xff0c;编译成功。如下图&#xff1a; 可是idea里面的源码&#xff0c;却标红了&#xff0c;如下&#xff1a; 错误…...

编程日记 2024/8/21 3:48:46

Linux基础环境开发工具gcc/g++ make/Makefile

1.Linux编译器-gcc/g使用 1. 预处理&#xff08;进行宏替换) 预处理功能主要包括宏定义,文件包含,条件编译,去注释等。 预处理指令是以#号开头的代码行。 实例: gcc –E hello.c –o hello.i 选项“-E”,该选项的作用是让 gcc 在预处理结束后停止编译过程。 选项“-o”是指目标…...

编程日记 2024/8/21 3:47:45

ES 模糊查询 wildcard 的替代方案探索

一、Wildcard 概述 Wildcard 是一种支持通配符的模糊检索方式。在 Elasticsearch 中&#xff0c;它使用星号 * 代表零个或多个字符&#xff0c;问号 ? 代表单个字符。 其使用方式多样&#xff0c;例如可以通过 {"wildcard": {"field_name": "value&…...

编程日记 2024/8/21 3:46:44

Linux安装MQTT 服务器（图文教程）

MQTT&#xff08;Message Queuing Telemetry Transport&#xff09;是一种轻量级的消息传输协议&#xff0c;专为低带宽和不稳定的网络环境设计&#xff0c;非常适合物联网&#xff08;IoT&#xff09;应用。 官网地址&#xff1a;https://www.emqx.com/ 一、版本选择 根据自己…...

编程日记 2024/8/21 3:43:41

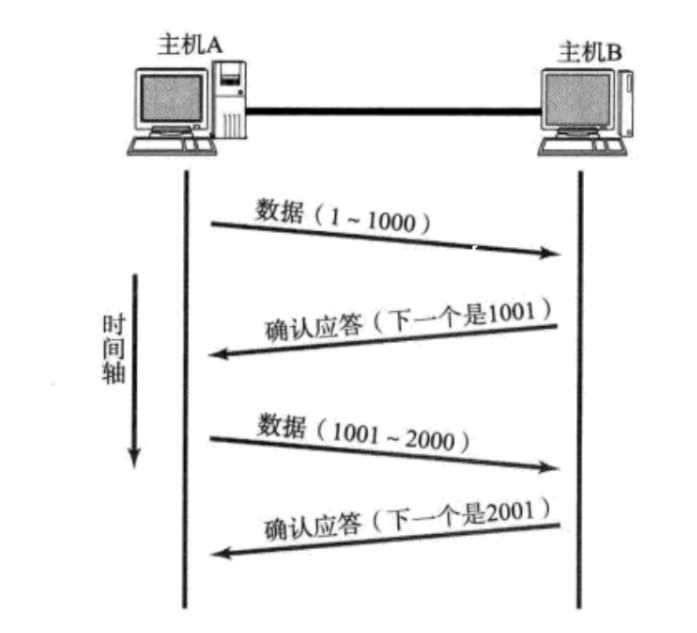
【TCP】核心机制：延时应答、捎带应答和面向字节流

文章目录 延时应答捎带应答面向字节流粘包问题方案一&#xff1a;指定分隔符方案二&#xff1a;指定数据的长度 TCP 报头首部长度保留&#xff08;6 位&#xff09;选项序号确认序号 延时应答 尽可能降低可靠传输带来的性能影响 提升性能>让滑动窗口变大 如果我们立即返回 …...

编程日记 2024/8/21 3:41:37

题解：AT_abc352_e [ABC352E] Clique Connect

[题目通道]([ABC352E] Clique Connect - 洛谷) 鄙人今日写人生第一篇题解 希望管理大大通过 首先&#xff0c;我们先看题: 它说一共有n个点&#xff0c;m回操作。。。 每次操作 都有 一个Ki 和 Ci Ki代表有Ki个点,Ci代表每条边所赋的边权 一看就知道这是个最小生成树的板子…...

编程日记 2024/8/21 3:40:36

【代码随想录训练营第42期 Day32打卡 - 从零开始动态规划 - LeetCode 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯

目录 一、做题心得 二、动规五步走 三、题目与题解 题目一&#xff1a;509. 斐波那契数 题目链接 题解1&#xff1a;记忆性递归 题解2&#xff1a;动态规划 题目二&#xff1a;70. 爬楼梯 题目链接 题解&#xff1a;动态规划 题目三&#xff1a;746. 使用最小花费爬楼…...

编程日记 2024/8/21 3:38:34

源码构建LAMP

目录 一、安装Apache 二、安装Mysql 三、安装PHP 四、安装论坛 一、安装Apache 1.cd 到opt目录下面&#xff0c;将压缩包拉进Xhell 2.解压缩apr和httpd压缩包 tar xf apr-1.6.2.tar.gz tar xf apr-util-1.6.0.tar.gz tar xf httpd-2.4.29.tar.bz2 3.将apr-1.6.2 移动到ht…...

编程日记 2024/8/21 3:35:31

Java：封装树结构

实体类 public class DictTreeselectVO {private String value;private String label;/*** 节点*/private String parentId;private List<DictTreeselectVO> children new ArrayList<DictTreeselectVO>();public String getValue() {return value;}public void s…...

编程日记 2024/8/21 3:31:26

linux内核 pintrl子系统

1、什么是pinctrl子系统 在 Linux 内核中&#xff0c;pinctrl子系统是一个专门用于管理和控制 SoC引脚复用和配置的子系统。SoC 通常具有大量的引脚&#xff08;pin&#xff09;&#xff0c;这些引脚可以被配置为不同的功能&#xff0c;比如 GPIO&#xff08;通用输入输出&…...

编程日记 2024/8/21 3:30:25

网络通信要素

网络介绍 定义&#xff1a;将具有独立功能的多台计算机通过通信线路和通信设备连接起来&#xff0c;在网络管理软件及网络通信协议下&#xff0c;实现资源共享和信息传递的虚拟平台。 学习网络的目的&#xff1a; 能够编写基于网络通信的软件或程序&#xff0c;通常来说就是网…...

编程日记 2024/8/21 3:29:24

day03_作业

一、简答题 继承的格式与好处 格式&#xff1a;class A extends B 好处&#xff1a;1.可以实现代码的复用&#xff0c;将共性的代码向上抽取&#xff0c;抽取到父类中。需要使用这些属性和行为的类&#xff0c;通过继承即可使用。2.当需要添加新的功能时&#xff0c;可以通过…...

编程日记 2024/8/21 3:28:23

pyinstaller程序打包，资源嵌入exe

参考&#xff1a;https://blog.csdn.net/qq_48979387/article/details/132359366 一、参数说明 -F 最终打包为一个可执行文件。-w 取消Windows显示窗口-add-data ‘dll;dll’&#xff0c;将当前目录dll下的文件打包到可执行文件的dll中&#xff0c;最终会在解压文件的dll文件…...

编程日记 2024/8/21 3:27:22

如何使用 OCR 和 GPT-4o mini 轻松提取收据信息

利用 OCR 和强大的 GPT-4o 迷你模型对收据进行信息提取 利用 OCR 和强大的 GPT-4o 迷你模型对收据进行信息提取 欢迎来到雲闪世界。&#xff0c;我将向您展示如何从收据中提取信息&#xff0c;并提供收据的简单图像。首先&#xff0c;我们将利用 OCR 从收据中提取信息。然后&a…...

编程日记 2024/8/21 3:26:20

椭圆曲线密码学(ECC)

一、ECC算法概述 椭圆曲线密码学&#xff08;Elliptic Curve Cryptography&#xff09;是基于椭圆曲线数学理论的公钥密码系统&#xff0c;由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA&#xff0c;ECC在相同安全强度下密钥更短&#xff08;256位ECC ≈ 3072位RSA…...

编程新知 2025/7/20 12:09:50

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】

微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来&#xff0c;Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

编程新知 2025/9/18 14:27:02

大语言模型如何处理长文本？常用文本分割技术详解

为什么需要文本分割？ 引言：为什么需要文本分割？一、基础文本分割方法1. 按段落分割（Paragraph Splitting）2. 按句子分割（Sentence Splitting）二、高级文本分割策略3. 重叠分割（Sliding Window）4. 递归分割（Recursive Splitting）三、生产级工具推荐5. 使用LangChain的…...

编程新知 2025/9/6 18:01:23

工程地质软件市场：发展现状、趋势与策略建议

一、引言 在工程建设领域&#xff0c;准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具&#xff0c;正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

编程新知 2025/9/9 8:26:07

HTML前端开发：JavaScript 常用事件详解

作为前端开发的核心&#xff0c;JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例&#xff1a; 1. onclick - 点击事件 当元素被单击时触发&#xff08;左键点击&#xff09; button.onclick function() {alert("按钮被点击了&#xff01;&…...

编程新知 2025/7/8 23:32:56

鱼香ros docker配置镜像报错：https://registry-1.docker.io/v2/

使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题&#xff1a;docker pull 失败 网络不同&#xff0c;需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

编程新知 2025/9/5 21:18:15

淘宝扭蛋机小程序系统开发：打造互动性强的购物平台

淘宝扭蛋机小程序系统的开发&#xff0c;旨在打造一个互动性强的购物平台&#xff0c;让用户在购物的同时&#xff0c;能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机&#xff0c;实现旋转、抽拉等动作&#xff0c;增…...

编程新知 2025/9/2 16:54:25

在 Spring Boot 项目里，MYSQL中json类型字段使用

前言&#xff1a; 因为程序特殊需求导致&#xff0c;需要mysql数据库存储json类型数据&#xff0c;因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

编程新知 2025/7/9 16:55:37

Kubernetes 网络模型深度解析：Pod IP 与 Service 的负载均衡机制，Service到底是什么？

Pod IP 的本质与特性 Pod IP 的定位 纯端点地址&#xff1a;Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址&#xff08;如 10.244.1.2&#xff09;无特殊名称&#xff1a;在 Kubernetes 中&#xff0c;它通常被称为 “Pod IP” 或 “容器 IP”生命周期&#xff1a;与 Pod …...

编程新知 2025/7/7 15:20:50

Ubuntu系统复制（U盘-电脑硬盘）

所需环境 电脑自带硬盘&#xff1a;1块 (1T) U盘1&#xff1a;Ubuntu系统引导盘&#xff08;用于“U盘2”复制到“电脑自带硬盘”&#xff09; U盘2&#xff1a;Ubuntu系统盘&#xff08;1T&#xff0c;用于被复制&#xff09; &#xff01;&#xff01;&#xff01;建议“电脑…...

编程新知 2025/9/13 17:36:53