迭代与递归
算法中会经常遇见重复执行某个任务,那么如何实现呢,本文将详细介绍两种实现方式,迭代与递归。
本文基于 Java 语言。
一、迭代
迭代(iteration),就是说程序会在一定条件下重复执行某段代码,直到条件不再满足。
在 Java 语言中,可以理解为就是循环遍历,Java 中有多种遍历方式,如 for 循环、while 循环。接下来讲解如何进行代码实现。
(一) for 循环
这个是最常见的迭代形式之一,适合在预先知道迭代次数(遍历次数)时使用。
比如,我们通过 for 循环计算1 + 2 + ... + n的结果。
public int forLoop(int n){int result = 0;for (int i = 0; i <= n; i++) {result += i;}return result;
}流程图如下:
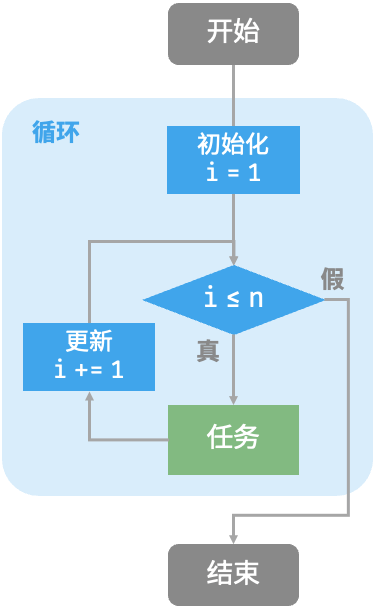
(二) while 循环
与 for 循环类似,while 循环也是一种实现迭代的方法。在 while 循环中,程序每轮都会先检查条件,如果条件为真,则继续执行,否则就结束循环。
比如,我们通过 while 循环计算1 + 2 + ... + n的结果。
public int whileLoop(int n) {int result = 0;int i = 1; // 初始化条件变量while (i <= n) {result += i;i++; // 更新条件变量}return result;
}(三) 嵌套循环
我们可以在一个循环结构内嵌套另一个循环结构,每一次嵌套都是一次“升维”,将会使时间复杂度提高至“立方关系”“四次方关系”,以此类推。
下面以冒泡排序为例,原理是从后两两对比,更小的往前放。数组内位置交换,不懂得话看一下我总结的另一篇文字--《位运算详解》。
public class FuXing {public static void main (String[] args) {int[] arr = {9,6,1,5,2,3,4,7,8};System.out.println("排序后:" + Arrays.toString( bubbleSort(arr)));}/*** 冒泡排序*/public static void bubbleSort (int[] arr){// 过滤无序排序的数组if(arr == null || arr.length < 2){return;}// 倒序遍历所有的数for (int i = arr.length - 1; i > 0; i--) {//两两比较,更小的往前放for (int j = 0; j < i; j++) {if(arr[j] > arr[j+1]){swap(arr,j,j+1);}}}}/*** 数组内位置交换*/public static void swap(int[] arr,int i ,int j){arr[i] ^= arr[j];arr[j] ^= arr[i];arr[i] ^= arr[j];}
}二、递归
(一) 简介
递归(recursion)是一种算法策略,通过直接或者间接地调用自身来解决问题,将大问题分解成更多的子问题,主要解决同一大类问题。
从数据结构角度看,递归天然适合处理链表、树和图的相关问题,因为它们非常适合用分治思想进行分析。
主要包含两个阶段:
- 递:程序不断深入地调用自身,通常传入更小或更简化的参数,直到达到“终止条件”。
- 归:触发“终止条件”后,程序从最深层的递归函数开始逐层返回,汇聚每一层的结果。
递归的三个重要要素(须记住):
- 终止条件:用于决定什么时候由“递”转“归”。
- 递归调用:对应“递”,函数调用自身。
- 返回结果:对应“归”,将当前递归层级的结果返回至上一层
(二) 如何设计递归
在写一些递归算法时,应该如何去操作呢?这里分享一点个人经验,当我们需要写一个递归程序时:
- 找重复:找到的相同的子问题;
- 找变化:聚焦于某一个子问题,查看变化的量,通常会作为参数,这时可定义函数体;
- 找出口:也就是找终止条件,这里注意关注返回值。
我们需要明确递归函数本身是为了做什么,返回值是什么,从最终想要的答案出发,逐步寻找上一层的答案,并且用它们构造当前层的答案。
比如,我们通过递归计算1 + 2 + ... + n结果。
- 找重复:n 的累加 = n + (n - 1)的累加,n - 1 就是原问题的重复,即子问题;
- 找变化:聚焦于某一个子问题,这里的变化就是 n 的自减,递归参数就是 n - 1;
- 找出口:当返回值为 1 时,终止条件就是
n = 1,n 为 1 时无法计算阶乘。
代码如下:
public int recursion (int n) {//终止条件if (n == 1) return 1;//递:递归调用int result = recursion(n - 1);//归:返回结果return result + n;}流程图如下:

(三) 调用栈
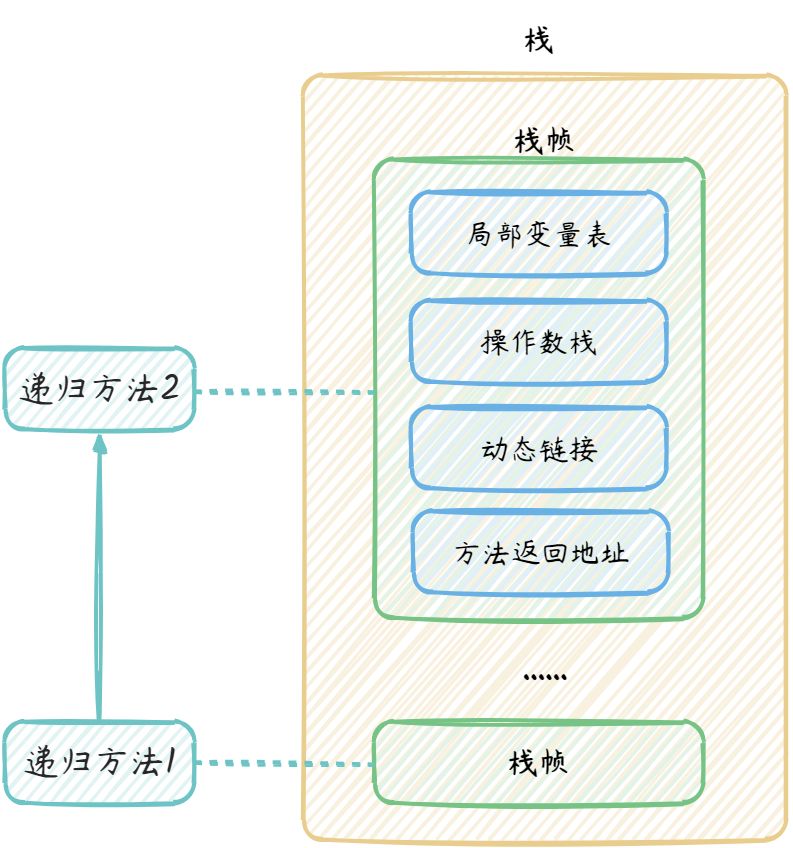
在 Java 中,递归函数每次调用自身时,JVM 都会为新开启的函数分配内存,以存储局部变量、调用地址和其他信息等。也就是在 Java 虚拟机栈中新生成一个栈帧。
因为栈空间是随着函数结果返回才会释放,所以递归通常比迭代更加消耗内存空间。且调用递归函数会产生额外的开销,因此时间效率上也会受影响。过深的递归操作,可能导致栈内存溢出。
(四) 尾部递归
如果函数在返回前的最后一步才进行递归调用,则该函数可以被编译器或解释器优化,使其在空间效率上与迭代相当。这种情况被称为尾递归(tail recursion)。
| 递归方式 | 说明 |
| 普通递归 | 当函数返回到上一层级的函数后,需要继续执行代码,因此系统需要保存上一层调用的上下文。 |
| 尾递归 | 递归调用是函数返回前的最后一个操作,这意味着函数返回到上一层级后,无须继续执行其他操作,因此系统无须保存上一层函数的上下文。 |
比如,还是通过递归计算1 + 2 + ... + n结果。尾部递归的求和操作是在“递”的过程中执行的,“归”的过程只需层层返回。而普通递归每层返回后都要再执行一次求和操作。
代码如下:
public int tailRecursion (int n, int result) {// 终止条件if (n == 0) return res;// 尾递归调用return tailRecursion(n - 1, res + n);}流程图如下:

(五) 递归树
当处理与“分治”相关的算法问题时,递归往往比迭代的思路更加直观、代码更加易读。以“斐波那契数列”为例。
斐波那契数列是指这样一个数列:0,1,1,2,3,5,8,13,21,34… 这个数列从第3项开始 ,每一项都等于前两项之和,求该数列的第 n 个数字。
回顾一下上面说的方法,进行设计递归函数:
1. 找重复:原问题的重复,即子问题。我们设斐波那契数列的第 n 个数字为 f(n),可得:
f(3) = f(2) + f(1) = 0;f(4) = f(3) + f(2) = 2;f(n) = f(n - 1) + f(n - 2);
这里每一项都等于前两项之和
2. 找变化:聚焦于某一个子问题,查看变化的量,会作为参数,这时可定义函数体。
如,f(n) = f(n - 1) + f(n - 2),这里的变化量有两个,n -1 和 n - 2,即分别做为入参。
函数体如下:
int fib(int n) {// 递归调用 f(n) = f(n-1) + f(n-2)int res = fib(n - 1) + fib(n - 2);// 返回结果 f(n)return res;
}3. 找出口:当返回值为 1 或 2 时,则会终止条件,n 为 1 或 2 时无法拆分为子问题,则完整函数如下。
int fib(int n) {// 终止条件 f(1) = 0, f(2) = 1if (n == 1 || n == 2) return n - 1;// 递归调用 f(n) = f(n-1) + f(n-2)int res = fib(n - 1) + fib(n - 2);// 返回结果 f(n)return res;
}观察以上代码,我们在函数内递归调用了两个函数,这意味着从一个调用产生了两个调用分支。如下图所示,这样不断递归调用下去,最终将产生一棵层数为 n 的递归树(recursion tree)。
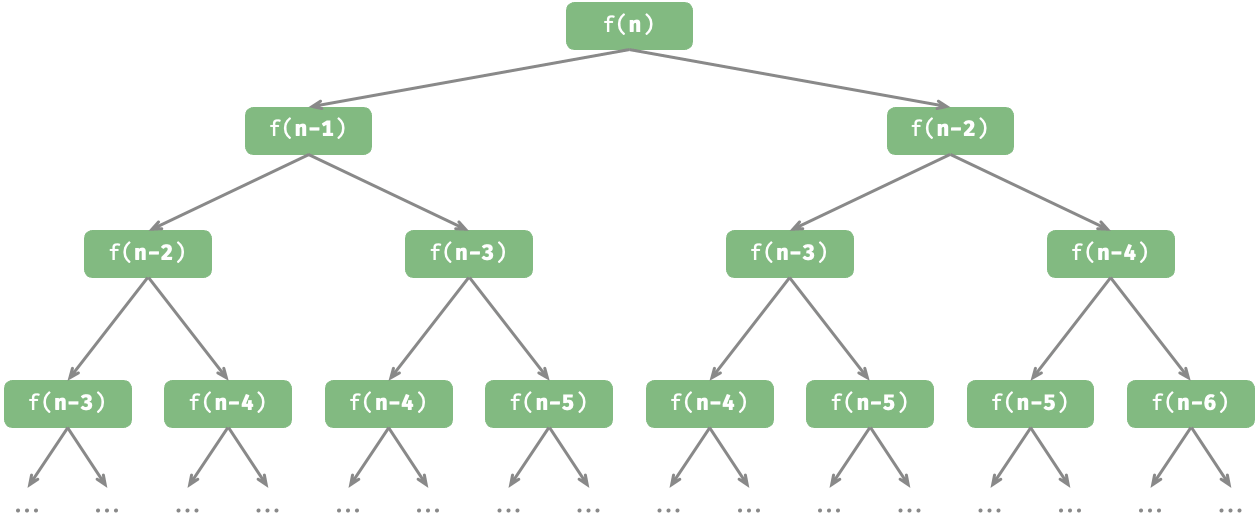
(六) 如何避免陷入递归
不知道你有没有被递归逻辑搞晕的经历,递归调用步骤中,经常会有很多深层操作,所以我们可能会想看看每一层的返回值,我们就会一层层深入的去思考下一步的逻辑,随着思考层数加深,就会觉得递归越来越困难,心态就崩了。
递归不像迭代是正向思维,是一个逆向思维的过程,很多情况其实并不好理解,也不清楚什么时候该用,很容易被层层嵌套搞晕。

那么如何解决这种问题呢?我们可以这么理解,迭代是正向思维,从已知去推未知,也就是从最开始的已知的基础步骤,不断的重复去累计,直到任务完成。
而递归是未知推已知,是将原问题分解成多个子问题,我们并不知道子问题的解,所以需要不断地通过递归分解,直到分解成基本的已知的解,最后在统一起来。
我们被搞晕的主要因素还是忍不住的跟随者递归函数去不断的深入思考,要想避免这种情况。只要我们不再探究它内部的深层操作,将所有的递归调用的操作当成一个整体,相信它自己就能完成使命。
比如,我们需要把大象装进冰箱,一共需要几步?是不是只要打开冰箱门,把大象放进去,然后关掉冰箱门。我们把大象放进冰箱当作终止条件,而递归调用过程当作把大象,我们并不需要知道大象怎么放进冰箱的,即我们不需要知道递归是怎么执行的。
这样我们在看一些递归算法时,可以避免陷入循环的递归逻辑中。
三、两者对比
| 对比维度 | 迭代 | 递归 |
| 实现方式 | 循环结构 | 函数调用自身 |
| 时间效率 | 效率通常较高,无函数调用开销 | 每次函数调用都会产生开销 |
| 内存使用 | 通常使用固定大小的内存空间 | 累积函数调用可能使用大量的栈空间 |
| 适用问题 | 适用于简单循环任务,代码直观、可读性好 | 适用于子问题分解,如树、图、分治、回溯等,代码结构简洁、清晰 |
尽管迭代和递归在很多情况下可以互相转化,但不一定值得这样做,有以下两点原因:
- 转化后的代码可能更加难以理解,可读性更差。
- 对于某些复杂问题,模拟系统调用栈的行为可能非常困难。
总之,选择迭代还是递归取决于特定问题的性质。在编程实践中,权衡两者的优劣并根据情境选择合适的方法至关重要。
参考:
[1] 靳宇栋. Hello 算法.
相关文章:

迭代与递归
算法中会经常遇见重复执行某个任务,那么如何实现呢,本文将详细介绍两种实现方式,迭代与递归。 本文基于 Java 语言。 一、迭代 迭代(iteration),就是说程序会在一定条件下重复执行某段代码,直…...

wo是如何克服编程学习中的挫折感的?
你是如何克服编程学习中的挫折感的? 编程学习之路上,挫折感就像一道道难以逾越的高墙,让许多人望而却步。然而,真正的编程高手都曾在这条路上跌倒过、迷茫过,却最终找到了突破的方法。你是如何在Bug的迷宫中找到出口的…...

vue3基础ref,reactive,toRef ,toRefs 使用和理解
文章目录 一. ref基本用法在模板中使用ref 与 reactive 的区别使用场景 二. reactive基本用法在模板中使用reactive 与 ref 的区别使用场景性能优化 三. toRef基本用法示例在组件中的应用主要用途对比 ref 和 toRef 四. toRefs基本用法示例在组件中的应用主要用途对比 ref 和 t…...

【Python机器学习】NLP的部分实际应用
自然语言处理在现实中非常多的应用,下表是其中的一些例子: 应用示例1示例2示例3搜索web文档自动补全编辑拼写语法风格对话聊天机器人助手行程安排写作索引用语索引目录电子邮件垃圾邮件过滤分类优先级排序文本挖掘摘要知识提取医学诊断法律法律断案先例…...

LLM 压缩之二: ShortGPT
0. 资源链接 论文: https://arxiv.org/pdf/2403.03853 项目代码: 待开源 1. 背景动机 现有的大语言模型 LLM 推理存在以下问题: LLM 模型因为 scale law 极大的提高模型的预测能力,但是同样带来较大的推理延时;对于 LLM 应用部署带来较大…...

EmguCV学习笔记 VB.Net 5.2 仿射变换
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 EmguCV是一个基于OpenCV的开源免费的跨平台计算机视觉库,它向C#和VB.NET开发者提供了OpenCV库的大部分功能。 教程VB.net版本请访问…...

Fink初识
文章目录 1. Flink核心组件2. Flink核心概念3. 执行应用程序的三种模式3.1 session mode3.2 per-job mode3.3 application mode 4. Job Manager4.1 Resource Manager4.2 Dispatcher4.3 Job Master 5. Watermark6. State7.时间属性7.1 处理时间 processing time7.2 事件时间 Eve…...

PyTorch的torchvision内置数据集使用,transform+pytorch联合使用
一、PyTorch的torchvision内置数据集介绍 我们前面的文章里谈到的数据集是我们自己找的一些自定义数据集。那么在Pytorch中存在2种数据集(Dataset),即内置数据集(Built-in dataset)和自定义数据集(Custom d…...

MT1619 (A/B/C对应18W/22W/25W)如何避免温度高、电磁干扰
MT1619系列是一款开关电源芯片,其内部集成了一颗高集成度、高性能的电流模式 PWM 控制器和一颗功率 MOSFET。MT1619 具有恒功率功能,特别适用于 PD 充电器、电源适配器等中小功率的开关电源设备。极低的启动电流与工作电流、以及轻载或者无负载情况下的 …...

Hadoop 的基本 shell 命令
Hadoop 的基本 shell 命令主要用于与 Hadoop 分布式文件系统(HDFS)和 MapReduce 进行交互。以下是一些常用的 Hadoop shell 命令: 一、 HDFS 命令 1. 查看 HDFS 状态 hdfs dfsadmin -report: 显示 HDFS 的健康状态和容量信息。 2. 文件系统操…...

HCIP-交换实验
根据实验要求,完成实验内容: 实验拓扑图如下所示 : 搭建拓补图: LSW1,LSW2: [LS1]interface Eth-Trunk 0 [LS1-Eth-Trunk0]q [LS1]interface g0/0/3 [LS1-GigabitEthernet0/0/3]eth-trunk 0 [LS1]interf…...
Windows下线程的创建与使用(win32-API)
一、前言 线程是比进程更轻量级的执行单元,允许在一个进程中并发执行多个控制流。每一个线程都有自己的程序计数器、寄存器集和栈空间,但它们共享所属进程的全局数据和资源。这种共享内存模型使线程间的通信比进程间通信更为高效,同时也带来…...
- 游戏分组)
华为OD机试(C卷,100分)- 游戏分组
题目描述 部门准备举办一场王者荣耀表演赛,有 10 名游戏爱好者参与,分为两队,每队 5 人。 每位参与者都有一个评分,代表着他的游戏水平。为了表演赛尽可能精彩,我们需要把 10 名参赛者分为示例尽量相近的两队。 一队的实力可以表示为这一队 5 名队员的评分总和。 现在给你…...

centos7.9系统按cloudpods
1. 简介: Cloudpods 是一款简单、可靠的企业IaaS资源管理软件。帮助未云化企业全面云化IDC物理资源,提升企业IT管理效率。 Cloudpods 帮助客户在一个地方管理所有云计算资源。统一管理异构IT基础设施资源,极大简化多云架构复杂度和难度&…...

android apk 加固后的地图加载异常及重新签名
1.首先根据需求将打包生成后的APK进行加固,可以使用360、阿里、腾讯加固等。 2.加固后的APK无法直接安装,需要重新进行签名。 3.首先找到sdk的位置,进入build-tools目录。 4.根据gradle文件选择版本目录。 5.将加固后的APK放至该目录下。在…...
手把手搭建私人在线备份系统
对于打工人来说,什么文件最重要? 那就是——打不开的文件最重要! 那么,如何才能避免这样的事情发生呢?这时候就需要使出我们的大杀器——文件备份! 文件备份怎么搞才最合适呢? 是使用移动硬盘&a…...
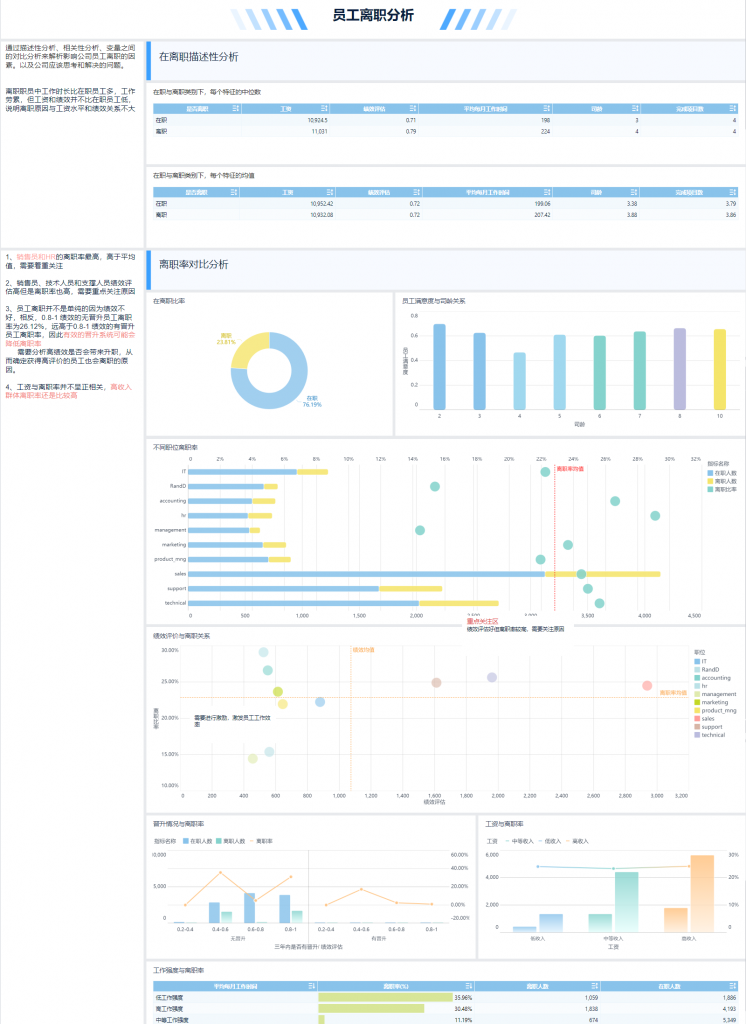
数据分析实操案例分享:如何对人事数据进行BI分析?
在数据驱动时代,数据分析已经成为企业和个人获取竞争优势的关键技能。特别是在人力资源管理领域,数据分析的应用正变得越来越重要。通过对在职和离职数据的深入分析,企业不仅能够洞察员工的动态,揭示员工流动的模式、预测人才需求…...

谷粒商城实战笔记-228-商城业务-认证服务-自定义SpringSession完成子域session共享
文章目录 一,228-商城业务-认证服务-自定义SpringSession完成子域session共享1. cookieSerializer()2. springSessionDefaultRedisSerializer() 一,228-商城业务-认证服务-自定义SpringSession完成子域session共享 前面弄清楚了分布式服务中的两个问题&…...

Elasticsearch核心
一、几个核心概念 1、节点:一个节点(Node)就是一个es进程,一个服务器可以部署多个节点 查询节点以及节点信息: http://127.0.0.1:9200/_cat/nodes?v 2、角色,是指节点在集群中担任什么角色:…...

Python.NET:打开Python与.NET世界互通的大门
Python.NET 是一个强大的工具,它为 Python 程序员提供了一种与 .NET 公共语言运行时 (CLR) 无缝集成的途径。它就像一座桥梁,将 Python 的灵活性与 .NET 的强大功能连接起来,为开发者提供了前所未有的自由和可能性。 1. Python.NET 的核心价值…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...

k8s从入门到放弃之Pod的容器探针检测
k8s从入门到放弃之Pod的容器探针检测 在Kubernetes(简称K8s)中,容器探测是指kubelet对容器执行定期诊断的过程,以确保容器中的应用程序处于预期的状态。这些探测是保障应用健康和高可用性的重要机制。Kubernetes提供了两种种类型…...
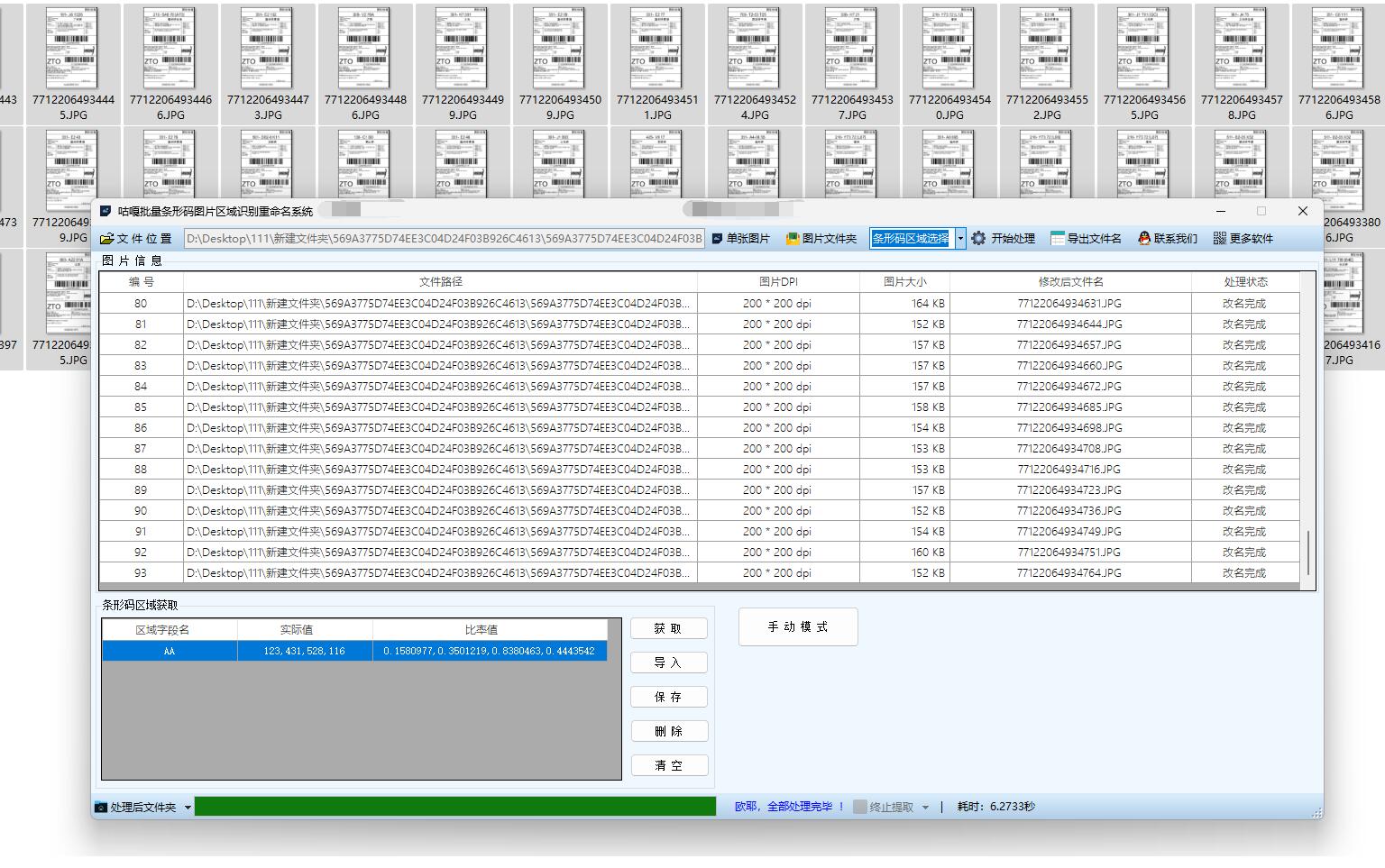
【工具教程】多个条形码识别用条码内容对图片重命名,批量PDF条形码识别后用条码内容批量改名,使用教程及注意事项
一、条形码识别改名使用教程 打开软件并选择处理模式:打开软件后,根据要处理的文件类型,选择 “图片识别模式” 或 “PDF 识别模式”。如果是处理包含条形码的 PDF 文件,就选择 “PDF 识别模式”;若是处理图片文件&…...
