整体思想以及取模
前言:一开始由于失误,误以为分数相加取模不能,但是其实是可以取模的
这个题目如果按照一般方法,到达每个节点再进行概率统计,但是不知道为什么只过了百分之十五的测试集
题目地址

附上没过关的代码
#include<bits/stdc++.h>
using namespace std;#define int long longint n; int ans = 0;
const int N = (int)2e6 + 5;
const int Mod = 998244353;
int e[N], ne[N], h[N / 2], idx = 0;
void add(int a, int b) {e[++idx] = b, ne[idx] = h[a], h[a] = idx;
}int qw(int x, int p) {int temp = 1;while (p) {if(p&1)temp = x * temp % Mod;x = x * x % Mod;p >>= 1;}return temp;
}void dfs(int u, int fa, int g, int step) {int cnt = 0;for (int i = h[u]; i; i = ne[i]) {int v = e[i]; if (fa == v) continue;cnt++;}if (cnt == 0) {// 已经是子节点了 //ans = (ans + (step % Mod) * qw(g, Mod - 2)) % Mod; return;ans = (ans + step*g%Mod) % Mod; return;}g = (g % Mod) * (qw(cnt, Mod - 2) % Mod) % Mod;for (int i = h[u]; i; i = ne[i]) {int v = e[i]; if (fa == v) continue;dfs(v, u, g , step + 1);}
}signed main() {cin >> n;for(int i=1;i<n;i++){int u,v; cin >> u >> v;add(u,v),add(v,u);}if(n==1){cout << 0 ; return 0;}dfs(1,0,1,0);cout << ans;return 0;
}
再写一个过关的,按照官方答案的解法的
#include<bits/stdc++.h>
using namespace std;#define int long longint n; int ans = 0;
const int N = (int)2e6 + 5;
const int Mod = 998244353;
const int P = 998244353;
int e[N], ne[N], h[N / 2], idx = 0;
vector<int> a[N / 2];
int siz[N], ye[N]; // 记录每一层的节点个数以及叶子节点的个数
void add(int a, int b) {e[++idx] = b, ne[idx] = h[a], h[a] = idx;
}int qw(int x, int p) {int temp = 1;while (p) {if (p & 1)temp = x * temp % Mod;x = x * x % Mod;p >>= 1;}return temp;
}void dfs(int u, int fa, int dep) {int cnt = 0; siz[dep]++;for (int i = h[u]; i; i = ne[i]) {int to = e[i]; if (to == fa) continue;cnt++; dfs(to, u, dep + 1);}if (cnt == 0) {ye[dep]++;}
}void solve() {int pre = 1; // 概率for (int i = 1; i < n; i++) {//cout << " siz " << i << " " << ye[i] << endl;if (siz[i] == 0) break;//ans = (ans+(pre*(ye[i]*(qw(siz[i],Mod-2),Mod-2)%Mod)%Mod) * (i)%Mod) % Mod;ans = (ans + pre * ye[i] % P * qw(siz[i], P - 2) % P * (i) % P) % P;pre = pre * ((siz[i] - ye[i]) * (qw(siz[i], Mod - 2)) % Mod)%Mod;//pre = pre * (((siz[i] - ye[i]) % P + P) % P) % P * qw(siz[i], P - 2) % P;}cout << ans; return;
}signed main() {cin >> n;for (int i = 1; i < n; i++) {int u, v; cin >> u >> v;add(u, v), add(v, u);//a[u].push_back(v); a[v].push_back(u);}if (n == 1) {cout << 0; return 0;}dfs(1, 0, 0);solve();return 0;
}
相关文章:

整体思想以及取模
前言:一开始由于失误,误以为分数相加取模不能,但是其实是可以取模的 这个题目如果按照一般方法,到达每个节点再进行概率统计,但是不知道为什么只过了百分之十五的测试集 题目地址 附上没过关的代码 #include<bits…...

RabbitMQ 消息可靠保障
RabbitMQ 消息可靠保障 消息的可靠性保证生产者重连生产者确认解决思路A-确认机制解决思路B-备份交换机 MQ 服务器宕机导致消息丢失消费端消息的可靠性保障 消费端限流给消息生成唯一id 消息的可靠性保证 实际项目中 MQ 的流程一般是:生产端把消息路由到交换机&…...

Redis 作为 PHP 的会话存储
使用 Redis 作为 PHP 的会话存储,可以实现多个服务器之间的会话共享,提高会话管理的效率,特别是在分布式系统中。这种方法将会话数据存储在 Redis 中,而不是使用默认的文件系统,从而使多个服务器可以访问相同的会话数据…...
基于伏图的数字心脏模拟仿真APP应用介绍
一、背景介绍 心脏是保证人体正常运转最重要的动力,人体内的血液循环通过心血管运输到各个部位,因此,心血管系统的稳定是人体健康的关键。心血管内科领域极具专业性,其理论研究与技术发展日新月异,心血管疾病患者往往…...

智云-一个抓取web流量的轻量级蜜罐docker一键启动
智云-一个抓取web流量的轻量级蜜罐docker安装教程 github地址 https://github.com/xiaoxiaoranxxx/POT-ZHIYUN docker快速启动(v1.4) git clone https://github.com/xiaoxiaoranxxx/POT-ZHIYUN.git cd POT-ZHIYUN docker-compose up -d默认映射到80和8080端口 mysql不对外开放…...

原生HTML5、CSS、JavaScript实现简易网易云音乐播放
1.效果图 2.源码 1.index.html <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>网易云音乐</title><link rel"stylesheet" href"../CSS/index.css"> </head>…...
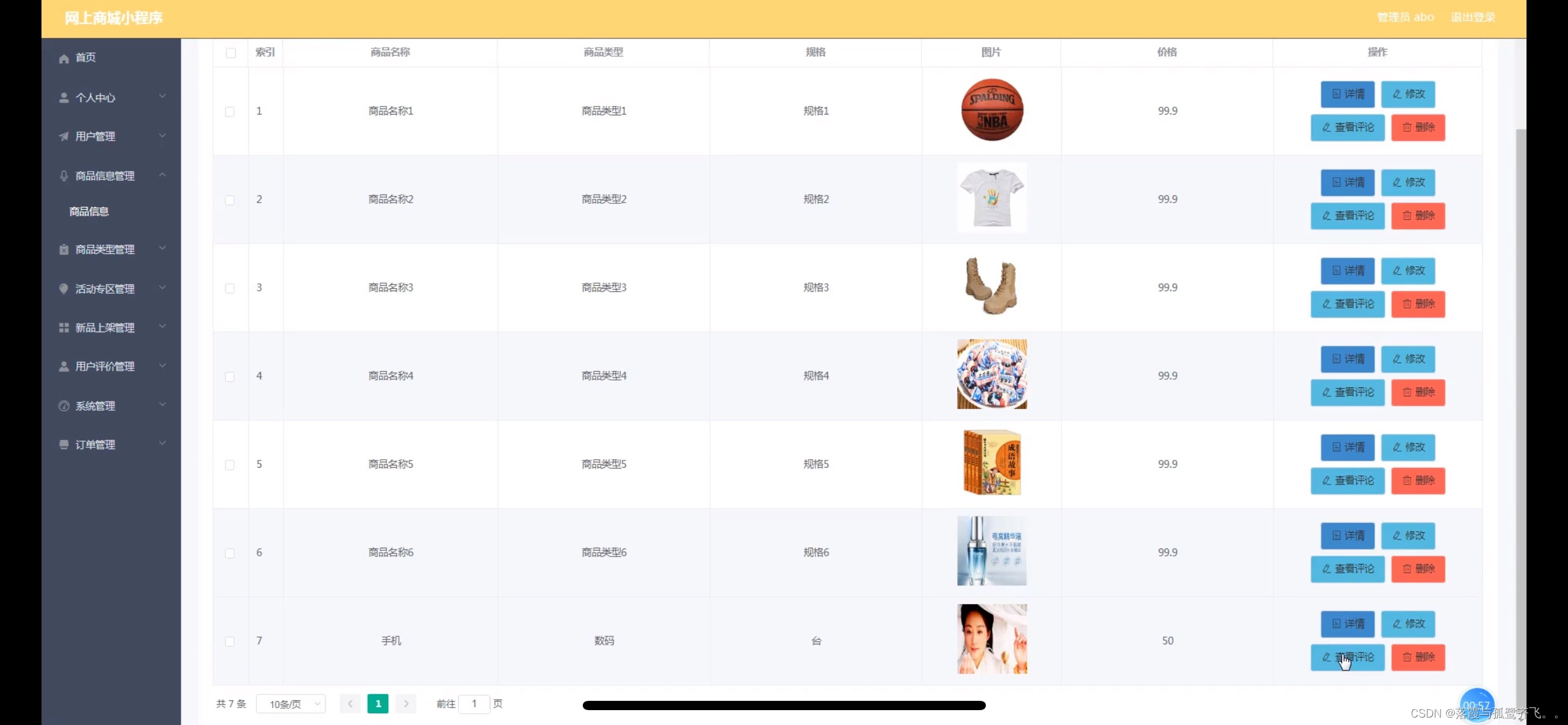
网上商城小程序的设计
管理员账户功能包括:系统首页,个人中心,用户管理,商品信息管理,商品类型管理,活动专区管理,新品上架管理,用户评价管理,订单管理,系统管理 微信端账号功能包…...

微分方程(Blanchard Differential Equations 4th)中文版Section2.2
动力系统的几何分析 捕食者-猎物系统的向量场 在第2.1节中,我们展示了两个不同捕食者-猎物系统的 R ( t ) R(t) R(t) 和 F ( t ) F(t) F(t) 图形,但没有描述我们是如何生成这些图形的。我们将在第2.5节中解决这个问题,采用欧拉方法推广到…...

Swift 环境搭建
Swift 环境搭建 Swift 是由苹果公司开发的一种强类型编程语言,用于iOS、macOS、watchOS和tvOS应用程序的开发。搭建Swift开发环境是开始使用Swift进行编程的第一步。本文将详细介绍如何在不同的操作系统上搭建Swift开发环境。 在macOS上搭建Swift环境 系统要求 …...

科技与出版
科技与出版 ISSN: 1005-0590 CN: 11-3209/G3 常设栏目:特别策划、产业观察、融媒之光、编辑实务、营销方略、学术探索、创作空间等。 稿件要求 (1)来稿应有创新性;立论科学,主题明确,推理严谨;词语准确,…...

5年前端面试之路
作者:星空海绵 顺便吆喝一声,技术大厂,内推捞人,前/后端or测试←感兴趣 --加班偶尔较多,但周末加班两倍工资。 --15-35K,工资一线城市属于一般,但二线城市很可以。 前言 由于公司要进行…...

产品运营(一)--产品运营是什么?
1.运营是什么? 通过一系列穿针引线式的行为和资源投入,让一件事能持续良性运转。 运营面向的主体不同,使用的运营手段也是不同的。作用:赋予产品闪耀的光芒。距离用户最近的人(体验用户,成为用户?demo:k…...

学习大数据DAY41 Hive 分区表创建
目录 分区表 分区表应用场景 oracle 分区表种类 oracle 分区-范围分区 oracle 分区-列表分区 oracle 分区-散列分区 oracle 分区-组合分区 oracle 分区-分区表操作 hive 分区-创建分区表 hive 分区-分区表操作 hive 分区-动态分区表配置 上机练习 分区表 分区是将一…...

【三维目标检测模型】ImVoteNet
【版权声明】本文为博主原创文章,未经博主允许严禁转载,我们会定期进行侵权检索。 参考书籍:《人工智能点云处理及深度学习算法》 本文为专栏《Python三维点云实战宝典》系列文章,专栏介绍地址“https://blog.csdn.net/suiyin…...

力扣 | 背包dp | 279. 完全平方数、518. 零钱兑换 II、474. 一和零、377. 组合总和 Ⅳ
文章目录 一、279. 完全平方数二、518. 零钱兑换 II三、474. 一和零四、377. 组合总和 Ⅳ 一、279. 完全平方数 LeetCode:279. 完全平方数 朴素想法: 这个题目最简单的想法是,可以用 O ( n n ) O(n\sqrt{}n) O(n n)的动态规划解决&#x…...

【ECMAScript性能优化的技巧与陷阱】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...

Swift实时监听判断是否连接有网络WIFI和蜂窝数据
本章节讲解如何使用swift连接网络,实时的监听到网络的状态,在主界面中进行调用,网络包含Wi-Fi 和 蜂窝。 1.封装一个判断是否有网络的类 2.在封装类注册通知 3.主界面接收注册通知,并且调用封装的网络类 4.成功测试,有…...
Flink Source 数据源)
(三)Flink Source 数据源
Flink 数据源主要分为内置数据源和第三方数据源。其中内置数据源包含文件、Socket 连接、集合类型数据等,不需要引入其它依赖库。第三方数据源定义了 Flink 和外部系统数据交互的逻辑,Flink 提供了非常丰富的数据源连接器,例如 Kafka、Elasticsearch、RabbitMQ、JDBC 等。 …...

第四届机电一体化、自动化与智能控制国际学术会议(MAIC 2024)
目录 大会官网 会议简介 组织机构 大会主席 程序委员会主席 主讲嘉宾 征稿主题 参会说明 大会官网 http://www.icmaic.org 会议简介 第四届机电一体化、自动化与智能控制国际学术会议(MAIC 2024)将于2024年9月27-29日在中国成都召开。MAIC 20…...
leetcode 089 打家劫舍
leetcode 089 打家劫舍 题目 一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响小偷偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。 给定…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...
