【C++ 第十五章】map 和 set 的封装(封装红黑树)
1. map 和 set 的介绍
⭐map 与 set 分别是STL中的两种序列式容器;
它们是一种树形数据结构的容器,且其的底层构造为一棵红黑树;
而在上一篇文章中提到,其实红黑树本身就是一棵二叉搜索树,是基于二叉搜索树的性质对其增加了平衡的属性来提高其综合性能
⭐当然也提到了红黑树与AVL树的区别:
1、AVL树保证了严格的平衡,其树高不会很高,使其查找效率较高,但是就是因为要不断旋转保证平衡,因此 当插入和删除时,较多的旋转会影响效率
2、红黑树不用保证严格的平衡,查找的时间复杂度为 O(logN) 级别(和AVL树)在 插入和删除 中,只需要较少的旋转,因此 插入和删除 效率较高
综合考虑 map 和 set 使用 红黑树作为底层容器
2. map 和 set 的结构
在 map 与 set 的使用过程中,由于 set 容器的底层树节点存储着数据为 key (T 类型)
而 map 的底层树节点存储着数据为一个键值对 key/value; (pair类型)
所以可能会联想到在STL中的这两个容器是否使用的是不同的红黑树?
而实际在 STL 的源码中可以看到,对于这两个容器而言所使用的是同一个红黑树(即调用同一棵红黑树),并且利用泛型的特性来控制两个容器中所使用的对应的参数;
那么既然是同一棵红黑树,应该如何对这棵树进行修改 使得该树能够同时兼容 map 的 key/value 键值对数据存储 和 set 的 key 数据存储 呢?
3、对红黑树的进一步修改
在我们的上一章节 讲解了红黑树的各种基础构造,本章对红黑树进一步修改,融入 迭代器 以及 泛型化使其更加适配 map 与 set
(1)修改一:将节点数据类型换成 T (泛型的思想)
将节点中数据变量 换成 类型T
当 T == key 类型时,该节点对应 set 容器
当 T == pair<key, value> 类型时,该节点对应 map 容器
这样就初步实现,同一节点类模板,可以对应 多种数据类型,适应 set 和 map
template<class T> struct RBTreeNode {T _data; // 泛型化思想:_data 可以是 Key 类型,也可以是 pair<Key, Value> 类型// ..... };
先前 set 和 map 要设计两套 红黑树类
为了适应 set:
template<class Key>
class RBTree
{}为了适应 map:
template<class Key, class Value>
class RBTree
{}现在节点类泛型化了,红黑树类也要对应修改
template<class T>
class RBTree
{}(2)修改二:应用仿函数 修改 插入函数 insert 内部比较逻辑
⭐之前没修改时,为了适应 set 和 map ,要设计两种传参类型
为了适应 set:
bool insert(const K& key) {}为了适应 map:
bool insert(const pair<K, V>& kv) {}
⭐insert 函数内部比较键值大小的部分 也有两套设计
当 T == key 时,对应 set,insert 函数内部比较键值大小的部分:直接比较键值 key
if (cur->_key < key) {// ..... }当 T == key/value 时,对应 map,insert 函数内部比较键值大小的部分:还要指定键值对的 first
if (cur->_kv.first < kv.first) {// ..... }
现在 节点数据泛型为 T,函数 insert 传参类型和内部某些比较逻辑都需要做调整
⭐ 修改传参类型
bool insert(const T& data)
{}⭐内部某些比较逻辑:使用仿函数
因为我们那里的就是要用 键值 key 比较,因此 set 可以直接用节点数据 key 比较,而 map 需要用 节点数据pair的first 比较,这里就有区别,因此需要仿函数“统一化”
(1)set :
使用仿函数时,当操作数类型为 K 类型,则直接识别使用 set 的仿函数 set_KeyOfT 中的 operator() 函数,返回 key(即返回一个键值)
template<class K>
class set
{// set 中的仿函数struct set_KeyOfT {const K& operator()(const K& key) {return key;}};// ....... 其他补充
private:RBTree<K, set_KeyOfT> _tree;
};(2)map
当操作数类型为 pair<key, value> 键值对类型,则直接识别为 map 的仿函数 map_KeyOfT 中的 operator() 函数,返回 pair<key, value> 的 first (即也返回一个 键值)
template<class K, class V>
class map
{struct map_KeyOfT {const K& operator()(const pair<K, V>& kv) {return kv.first;}};// ....... 其他补充private:RBTree<pair<const K, V>, map_KeyOfT> _tree;
};在 红黑树类模板中添加 仿函数的类型:class KeyOfT
template<class T, class KeyOfT>
class RBTree
{}仿函数的应用
KeyOfT kot; // 创建一个仿函数类对象
if (kot(cur->_data) < kot(data)) // data 可能是 key类型,可能是 pair<key, value> 类型
// 使用仿函数,调用operator() 自动识别 data 的类型,放回 键值 key 进行比较(3)修改三:给 红黑树类模板 再加一个 类型 class K
我们实现 find 和 insert 函数时,insert 函数参数类型是 T ,表示 data 可以是 key 类型,也可以是 pair< key, value > 类型
但是 find 函数参数可以是 T 类型吗??
不可以!,无论是 map or set,find 函数都是查找 键值 key,固定要用 key
若 find 的参数是 T 类型,当 T == key 时,直接可以使用,当 T == pair< key, value > 时,就不能直接使用 T 来查找,就要使用 T.first,就使得两个类型造就两种使用逻辑
因此 我们可以额外传一个 键值(既然是固定要用的,就多传一个)
template<class K, class T, class KeyOfT>
class RBTree
{}
至此,我们红黑树类模板中 第一个参数 K 用于传键值key,第二个参数 T 为泛型用于 接收两种类型(兼容set 和 map 两种),第三个参数为 仿函数
(4)修改四:插入函数 insert 的 返回值 改为 pair 类型
在STL中,无论是 map 容器还是 set 容器,其插入函数Insert()函数的返回值都是为一个pair<iterator,bool>;
1、若是插入成功则返回新插入节点的迭代器位置 与 true; (迭代器的实现将在下文中提到)
2、若是插入失败则返回与需要插入的数据相同的节点位置 与 false;
例如 STL 库中的 map 的 insert 函数源码
pair<iterator,bool> insert (const value_type& val);value_type 就是 pair< K, V>
pair 是一个类模板
我们的 插入函数 返回值修改为:
pair<iterator, bool> insert(const T& data)4. 迭代器
因为需要将 红黑树封装进容器 map 和 set 中,容器会涉及各种操作,需要迭代器
因此我们先实现 红黑树的迭代器
因为 map 和 set 的底层是 红黑树,因此 他们的 迭代器就是将一个树节点指针封装成一个类
1.1 基础类框架和函数
基础函数:重载点操作符、重载箭头操作符、重载不等于操作符、构造函数
template<class T, class Ref, class Ptr> struct RBTreeIterator {typedef RBTreeNode<T> Node;typedef RBTreeIterator<T, Ref, Ptr> Self;Node* _p;Ref operator*() {return _p->_data;}Ptr operator->() {return &(_p->_data);}// 两个迭代器比较相等 就是直接比较 两个指针bool operator!=(const Self& x) {return _p != x._p;}RBTreeIterator(Node* p):_p(p){} };
1.2 重载前置++ 和 前置--
关于前置++
在 二叉搜索树中 前置++,需要使迭代器指向 中序遍历的 下一个位置
因此,设计前置++ 就需要模拟中序遍历找到下一个节点

中序遍历顺序是:左孩子 ---> 根 ---> 右孩子
若当前节点为 节点 5,按照中序,下一个位置是 节点 7,即 根节点(从左孩子到根节点)
若当前节点为 节点 7,按照中序,下一个位置是 节点 9,即 右孩子(从根节点到右孩子)
若当前节点为 节点 9,按照中序,右孩子为 空,证明已经走完一个中序(左根右),应该回溯到 祖先节点,寻找 当前节点为 父亲的左孩子的关系,即 从节点9 一直到 节点 7,此时 节点7 是父亲节点 11 的左孩子(这样满足 从左孩子到根节点 ,即节点 9 的下一个位置就是 节点 11)
若当前节点为 节点 11,按照中序,下一个位置是 节点 12,即右子树的 最左节点(在右子树,循环向下找到右子树的最左节点)
综合上面几种情况,可以得出以下逻辑
1、右不为空,则 自己就是 根:右子树最左节点就是中序下一个,while() 循环 找 右子树的 最左节点
2、右为空,则 cur 和 parent 沿着到根节点的路径向上查找,直到 孩子 cur 是父亲 parent 的 left
此时 parent 就是中序的下一个节点
伪代码:
定义 cur = 当前位置
if(cur 的 右不为空)
循环找右子树的最左节点
else if(cur 的 右为空)
定义 parent
while(parent 不为 空 且 parent 的左 不为 cur)
循环结束,parent 就是 中序的写一个节点
实际代码:
Self& operator++() {Node* cur = _p;if (cur->_right) {cur = cur->_right;while (cur->_left) { // 注意这里是 cur->_left 我们目的是到最左节点,不是 空节点!cur = cur->_left;}}else {Node* parent = cur->_parent;while (parent && parent->_left != cur) {cur = parent;parent = parent->_parent;}cur = parent;}_p = cur;return *this; }
关于前置--
重载前置-- 也 同理,就是倒着中序遍历(右 根 左)
注意:前置-- 的第一个节点可能为 end(),本文中我们将 end() 设置为 最后一个节点的下一个节点,即为 NULL
当对 end() == NULL 前置-- 时,可能导致空指针访问的错误,因此需要特殊处理
end() 的前一个即为 二叉树的 最后一个节点(中序遍历的最后一个:右子树的最右节点)
Node* cur = _p; // 如果 cur 为 nullptr 代表现在指向 end() // 特殊处理 if (cur == nullptr) {cur = _root;while (cur && cur->_right) {cur = cur->_right;}//_p = cur; }
前置-- 的代码:
// 减减 和 加加的 逻辑刚好相反 Self& operator--() {Node* cur = _p;// 如果 cur 为 nullptr 代表现在指向 end()// 特殊处理if (cur == nullptr) {cur = _root;while (cur && cur->_right) {cur = cur->_right;}//_p = cur;}// 下面的逻辑和 前置++ 差不多:镜像反转理解即可else if (cur->_left) {cur = cur->_left;while (cur->_right) {cur = cur->_right;}}else {Node* parent = cur->_parent;while (parent && parent->_right != cur) {cur = parent;parent = parent->_parent;}cur = parent;}_p = cur;return *this; }
1.3 将 迭代器封装进 红黑树
这里定义了:begin() / end() (且为 iterator 和 const_iterator 两个版本)
此处:红黑树的 begin 是整棵二叉搜索树的 最左边的节点(即中序遍历的第一个节点),因此需要循环操作
template<class K, class T, class KeyOfT> class RBTree { public:typedef RBTreeNode<T> Node;// 定义迭代器typedef RBTreeIterator<T, T&, T*> iterator;typedef RBTreeIterator<T, const T&, const T*> const_iterator;// 迭代器iterator begin() {Node* cur = _root;while (cur && cur->_left) {cur = cur->_left;}return iterator(cur, _root);}iterator end() {return iterator(nullptr, _root);}const_iterator begin() const {Node* cur = _root;while (cur && cur->_left) {cur = cur->_left;}return const_iterator(cur, _root);}const_iterator end() const {return const_iterator(nullptr, _root);}private:Node* _root = nullptr; };
就是上面这一部分封装了迭代器,其他的红黑树代码部分上一章都实现了,这里暂不赘述
1.4 ⭐ 迭代器类 完整代码
注释都有解释了,若不明白,可以评论区讨论或私信
// T :节点中的数据类型
// Ref:引用类型 T& 或 const T&
// Ptr:指针类型 T* 或 const T*
template<class T, class Ref , class Ptr>
struct RBTreeIterator
{typedef RBTreeNode<T> Node; // 重定义节点类命名typedef RBTreeIterator<T, Ref, Ptr> Self; // 对自己的迭代器类型重命名Node* _p; // 迭代器中指向节点的指针Ref operator*() {return _p->_data;}Ptr operator->() {return &(_p->_data);}// 两个迭代器比较相等 就是直接比较 两个指针bool operator!=(const Self& x) {return _p != x._p;}bool operator==(const Self& x) const {return _p == x._p;}// 我写的函数 cur 有点冗余,其实代码可以更加精简Self& operator++() {Node* cur = _p;if (cur->_right) {cur = cur->_right;while (cur->_left) { // 注意这里是 cur->_left 我们目的是到最左节点,不是 空节点!cur = cur->_left;}}else {Node* parent = cur->_parent;while (parent && parent->_left != cur) {cur = parent;parent = parent->_parent;}cur = parent;}_p = cur;return *this;}// 减减 和 加加的 逻辑刚好相反Self& operator--() {Node* cur = _p;// 如果 cur 为 nullptr 代表现在指向 end()// 特殊处理if (cur == nullptr) {cur = _root;while (cur && cur->_right) {cur = cur->_right;}//_p = cur;}// 下面的逻辑和 前置++ 差不多:镜像反转理解即可else if (cur->_left) {cur = cur->_left;while (cur->_right) {cur = cur->_right;}}else {Node* parent = cur->_parent;while (parent && parent->_right != cur) {cur = parent;parent = parent->_parent;}cur = parent;}_p = cur;return *this;}RBTreeIterator(Node* p, Node* root):_p(p){}
};5. ⭐红黑树 完全体(含迭代器+适配 map 和 set 的泛型)
含有
红黑树节点类
迭代器类
红黑树类:拷贝构造、赋值运算符重载、析构、插入函数、4种旋转函数、查找 find、中序遍历、求树的高度、求树的节点个数、判断树是否平衡
#pragma once
#include<iostream>
#include<vector>
#include<assert.h>
using namespace std;// 设置颜色枚举值
enum Colour {RED,BLACK
};template<class T>
struct RBTreeNode
{typedef RBTreeNode<T> Node;T _data; // 泛型化思想:_data 可以是 Key 类型,也可以是 pair<Key, Value> 类型Node* _left;Node* _right;Node* _parent;Colour _col;RBTreeNode(const T& data):_data(data), _left(nullptr), _right(nullptr), _parent(nullptr){}
};// T :节点中的数据类型
// Ref:引用类型 T& 或 const T&
// Ptr:指针类型 T* 或 const T*
template<class T, class Ref , class Ptr>
struct RBTreeIterator
{typedef RBTreeNode<T> Node; // 重定义节点类命名typedef RBTreeIterator<T, Ref, Ptr> Self; // 对自己的迭代器类型重命名Node* _p; // 迭代器中指向节点的指针Node* _root; Ref operator*() {return _p->_data;}Ptr operator->() {return &(_p->_data);}// 两个迭代器比较相等 就是直接比较 两个指针bool operator!=(const Self& x) {return _p != x._p;}bool operator==(const Self& x) const {return _p == x._p;}// 我写的函数 cur 有点冗余,其实代码可以更加精简Self& operator++() {Node* cur = _p;if (cur->_right) {cur = cur->_right;while (cur->_left) { // 注意这里是 cur->_left 我们目的是到最左节点,不是 空节点!cur = cur->_left;}}else {Node* parent = cur->_parent;while (parent && parent->_left != cur) {cur = parent;parent = parent->_parent;}cur = parent;}_p = cur;return *this;}// 减减 和 加加的 逻辑刚好相反Self& operator--() {Node* cur = _p;// 如果 cur 为 nullptr 代表现在指向 end()// 特殊处理if (cur == nullptr) {cur = _root;while (cur && cur->_right) {cur = cur->_right;}//_p = cur;}// 下面的逻辑和 前置++ 差不多:镜像反转理解即可else if (cur->_left) {cur = cur->_left;while (cur->_right) {cur = cur->_right;}}else {Node* parent = cur->_parent;while (parent && parent->_right != cur) {cur = parent;parent = parent->_parent;}cur = parent;}_p = cur;return *this;}RBTreeIterator(Node* p, Node* root):_p(p),_root(root){}
};template<class K, class T, class KeyOfT>
class RBTree
{
public:typedef RBTreeNode<T> Node;typedef RBTreeIterator<T, T&, T*> iterator;typedef RBTreeIterator<T, const T&, const T*> const_iterator;RBTree() = default;~RBTree() {destory(_root);_root = nullptr;}// 拷贝构造RBTree(const RBTree<K, T, KeyOfT>& t) {_root = CopyTree(t._root);}// 赋值重载RBTree<K, T, KeyOfT>& operator=(const RBTree<K, T, KeyOfT>& t) {RBTree tmp(t);std::swap(_root, tmp._root);return *this;}// 迭代器iterator begin() {Node* cur = _root;while (cur && cur->_left) {cur = cur->_left;}return iterator(cur, _root);}iterator end() {return iterator(nullptr, _root);}const_iterator begin() const {Node* cur = _root;while (cur && cur->_left) {cur = cur->_left;}return const_iterator(cur, _root);}const_iterator end() const {return const_iterator(nullptr, _root);}// 查找iterator find(const K& key) const {Node* cur = _root;while (cur) {if ((cur->_data).first < key) {cur = cur->_right;}else if ((cur->_data).first > key) {cur = cur->_left;}else return iterator(cur, _root);}return end();}// 插入// 插入成功就是 true,迭代器指向新插入的节点// 插入失败就是 false,迭代器指向已存在的那个节点pair<iterator, bool> insert(const T& data) {if (_root == nullptr) {_root = new Node(data);_root->_col = BLACK; // 根节点一定是黑的return make_pair(iterator(_root, _root), true);}// 利用仿函数KeyOfT kot;Node* cur = _root;Node* parent = cur;while (cur) {if (kot(cur->_data) < kot(data)) {parent = cur;cur = cur->_right;}else if (kot(cur->_data) > kot(data)) {parent = cur;cur = cur->_left;}else return make_pair(iterator(cur, _root), false);}// 在 cur 的位置插入该节点cur = new Node(data);cur->_col = RED; // 新增节点给 红的Node* newNode = cur; // 这里记录以下初始的 cur,避免下面各种操作改变 cur// 父连子,子连父if (kot(parent->_data) > kot(data)) parent->_left = cur;else parent->_right = cur;cur->_parent = parent;// 变色调整:while (parent && parent->_col == RED) {Node* Grandfather = parent->_parent;/*gp u*/// 父亲是 爷爷 的左孩子if (parent == Grandfather->_left) {Node* Uncle = Grandfather->_right;// 叔叔是 红色:三人变色,cur指爷if (Uncle && Uncle->_col == RED) {parent->_col = BLACK;Uncle->_col = BLACK;Grandfather->_col = RED;cur = Grandfather;parent = cur->_parent;}// 叔叔是 黑色:旋转后变色else if (Uncle == nullptr || Uncle->_col == BLACK) {// 看 cur 的位置:决定单旋 or 双旋if (cur == parent->_left) { /* 右单旋 + 变色gp uc*/rotateLL(Grandfather);// 爷变红,父变黑Grandfather->_col = RED;parent->_col = BLACK;}else if (cur == parent->_right) {/* 双旋(先左旋后右旋) + 变色gp uc*/rotateRR(parent); // p 先 左旋rotateLL(Grandfather); // g 再右旋// 爷变红,cur 变黑Grandfather->_col = RED;cur->_col = BLACK;}break;}}// 父亲是 爷爷 的右孩子else if (parent == Grandfather->_right) {Node* Uncle = Grandfather->_left;// 叔叔是 红色:三人变色,cur指爷if (Uncle && Uncle->_col == RED) {parent->_col = BLACK;Uncle->_col = BLACK;Grandfather->_col = RED;cur = Grandfather;parent = cur->_parent;}// 叔叔是 黑色:旋转后变色else if (Uncle == nullptr || Uncle->_col == BLACK) {// 看 cur 的位置:决定单旋 or 双旋if (cur == parent->_right) {/* 左单旋 + 变色gu pc*/rotateRR(Grandfather);// 爷变红,父变黑Grandfather->_col = RED;parent->_col = BLACK;}else if (cur == parent->_left) {/* 双旋(先右旋后左旋) + 变色gu pc*/rotateLL(parent); // p 先 右旋rotateRR(Grandfather); // g 再左旋// 爷变红,cur 变黑Grandfather->_col = RED;cur->_col = BLACK;}break;}}}// 修改一:根节点强制变色_root->_col = BLACK;return make_pair(iterator(newNode, _root), true);}// RR型:左单旋void rotateRR(Node* parent) {Node* subR = parent->_right;Node* subRL = subR->_left;Node* parentParent = parent->_parent;// 1、subRL变成parent的右孩子parent->_right = subRL;// subRL 是有可能为 空的if (subRL) {subRL->_parent = parent;}// 2、parent变成subR的左孩子subR->_left = parent;parent->_parent = subR;// 3、subR变成当前子树的根// parentParent 是指 刚开始的 parent 的父亲:若 parent 是 _root 则 parentParent 为空,否则不为空,则该树就是子树if (parentParent) {if (parent == parentParent->_right)parentParent->_right = subR;else parentParent->_left = subR;subR->_parent = parentParent;}// 如果 parentParent == nullptr:说明 parent 是该树的 _root,_root 的 parent 是空else {_root = subR;subR->_parent = nullptr;}}// LL型:右单旋void rotateLL(Node* parent) {Node* subL = parent->_left;Node* subLR = subL->_right;Node* parentParent = parent->_parent;// 1、subLR变成parent的左孩子parent->_left = subLR;// subRL 是有可能为 空的if (subLR) {subLR->_parent = parent;}// 2、parent变成subL的右孩子subL->_right = parent;parent->_parent = subL;// 3、subL 变成当前子树的根// parentParent 是指 刚开始的 parent 的父亲:若 parent 是 _root 则 parentParent 为空,否则不为空,则该树就是子树if (parentParent) {if (parent == parentParent->_right)parentParent->_right = subL;else parentParent->_left = subL;subL->_parent = parentParent;}// 如果 parentParent == nullptr:说明 parent 是该树的 _root,_root 的 parent 是空else {_root = subL;subL->_parent = nullptr;}}// LR 型:subL 先 左旋, parent 右旋void rotateLR(Node* parent) {rotateRR(parent->_left);rotateLL(parent);}// RL 型:subR 先 右旋, parent 左旋void rotateRL(Node* parent) {rotateLL(parent->_right);rotateRR(parent);}// 中序遍历void InOrder() {_InOrder(_root);cout << '\n';}// 获取根节点Node* GetRoot() {return _root;}// 获取该树的高度int Height() {return _Height(_root);}// 获取节点个数int Size() {return _Size(_root);}// 判断是否是 红黑树bool IsValidRBTree() {if (_root == nullptr) return false;else if (_root && _root->_col == RED) return false;// 遍历一条路,记录一条路上一共固定有多少个黑色节点int cnt = 0;Node* cur = _root;while (cur) {if (cur->_col == BLACK) cnt++;cur = cur->_left;}return _IsValidRBTree(_root, 0, cnt);}private:// 判断是否是 红黑树bool _IsValidRBTree(Node* pRoot, size_t k, const size_t blackCount){// 1、看根节点是否是 黑的// 2、看每条路径的 黑色节点数量是否相同// 3、检查是否有连续的红节点:遇到一个红节点就判断其父亲是否是 红的//走到null之后,判断 k 和 blackCount 是否相等:即一条路径上的 黑色节点数量是否为固定值if (pRoot == nullptr){if (k != blackCount){cout << "违反性质四:每条路径中黑色节点的个数必须相同" << endl;return false;}return true;}// 统计黑色节点的个数if (pRoot->_col == BLACK)k++;// 检测当前节点与其双亲是否都为红色Node* pParent = pRoot->_parent;if (pParent && pParent->_col == RED && pRoot->_col == RED){cout << "违反性质三:没有连在一起的红色节点" << endl;return false;}return _IsValidRBTree(pRoot->_left, k, blackCount) && _IsValidRBTree(pRoot->_right, k, blackCount);}int _Size(Node* pRoot) {if (pRoot == nullptr) return 0;//if (pRoot->_left == nullptr && pRoot->_right == nullptr) return 1;return 1 + _Size(pRoot->_left) + _Size(pRoot->_right);}int _Height(Node* pRoot) {if (pRoot == nullptr)return 0;return 1 + max(_Height(pRoot->_left), _Height(pRoot->_right));}// 销毁一棵树:后序遍历void destory(Node* root) {if (root == nullptr) {return;}destory(root->_left);destory(root->_right);delete root;}// 拷贝一棵树Node* CopyTree(const Node* root) {if (root == nullptr) {return nullptr;}Node* newRoot = new Node(root->_kv);newRoot->_left = CopyTree(root->_left);newRoot->_right = CopyTree(root->_right);return newRoot;}void _InOrder(const Node* root) {if (root == nullptr) {return;}_InOrder(root->_left);cout << (root->_kv).first << " : " << (root->_kv).second << '\n';_InOrder(root->_right);}Node* _root = nullptr;
};6. ⭐封装 set 完整代码
红黑树的代码 前面已经实现,在 set 中直接调用一个红黑树即可(记得在 set.h 要放入 红黑树的头文件 )
template<class K>
class set
{struct set_KeyOfT {const K& operator()(const K& key) {return key;}};
public:typedef typename RBTree<K, const K, set_KeyOfT>::iterator iterator;typedef typename RBTree<K, const K, set_KeyOfT>::const_iterator const_iterator;// 直接调用红黑树的 插入函数pair<iterator, bool> insert(const K& key) {return _tree.insert(key);}// 迭代器:都是直接调用底层红黑树的 函数iterator begin() {return _tree.begin();}iterator end() {return _tree.end();}const_iterator begin() const {return _tree.begin();}const_iterator end() const {return _tree.end();}iterator find(const K& key) {return _tree.find(key);}private:RBTree<K, const K, set_KeyOfT> _tree;
};7. ⭐封装 map 完整代码
红黑树的代码 前面已经实现,在 map 中直接调用一个红黑树即可(记得在 map .h 要放入 红黑树的头文件 )
template<class K, class V>
class map
{struct map_KeyOfT {const K& operator()(const pair<K, V>& kv) {return kv.first;}};
public:typedef typename RBTree<K, pair<const K, V>, map_KeyOfT>::iterator iterator;typedef typename RBTree<K, pair<const K, V>, map_KeyOfT>::const_iterator const_iterator;pair<iterator, bool> insert(const pair<K, V>& kv) {return _tree.insert(kv);}// 迭代器iterator begin() {return _tree.begin();}iterator end() {return _tree.end();}const_iterator begin() const {return _tree.begin();}const_iterator end() const {return _tree.end();}iterator find(const K& key) {return _tree.find(key);}V& operator[](const K& key) {pair<iterator, bool> pr = insert(make_pair(key, V()));return pr.first->second;}private:RBTree<K, pair<const K, V>, map_KeyOfT> _tree;
};
相关文章:

【C++ 第十五章】map 和 set 的封装(封装红黑树)
1. map 和 set 的介绍 ⭐map 与 set 分别是STL中的两种序列式容器; 它们是一种树形数据结构的容器,且其的底层构造为一棵红黑树; 而在上一篇文章中提到,其实红黑树本身就是一棵二叉搜索树,是基于二叉搜索树的性质对其增加了平衡的属性来提高其综合性能 ⭐当然也…...

LIN通讯
目录 1 PLinApi.h 2 TLINFrameEntry 结构体 3 自定义函数getTLINFrameEntry 4 TLINScheduleSlot 结构体 5 自定义函数 getTLINScheduleSlot 6 自定义LIN_SetScheduleInit函数 7 自定义 LIN_StartSchedule 8 发送函数 9 线程接收函数 1 PLinApi.h 这是官方头文件 ///…...
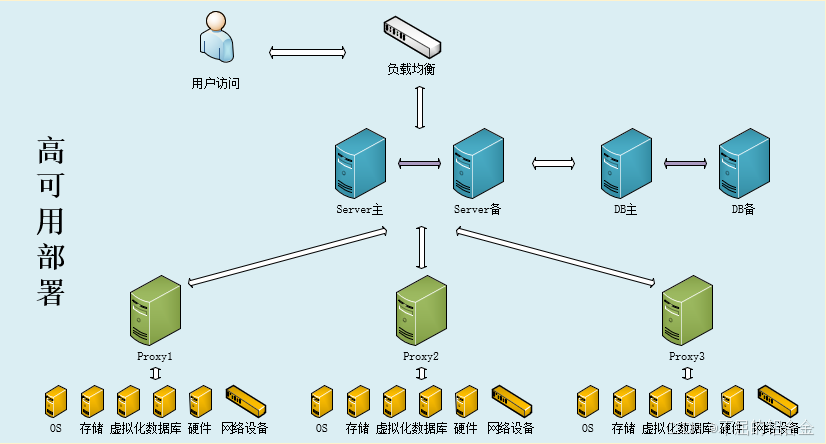
zabbix常见架构及组件
Zabbix作为一个开源的、功能全面的监控解决方案,广泛应用于各类组织中,以实现对网络、服务器、云服务及应用程序性能的全方位监控。部署架构灵活性高,可支持从小型单一服务器环境到大型分布式系统的多种场景。基本架构通常包括监控端…...
plsql表格怎么显示中文 plsql如何导入表格数据
在Oracle数据库开发中,PL/SQL Developer是一款广泛使用的集成开发环境(IDE),它提供了丰富的功能来帮助开发人员高效地进行数据库开发和管理。在使用PL/SQL Developer时,许多用户会遇到表格显示中文的问题,以…...

chromedriver下载地址大全(包括124.*后)以及替换exe后仍显示版本不匹配的问题
Chrome for Testing availability CNPM Binaries Mirror 若已经更新了系统环境变量里的chromdriver路径下的exe,仍显示版本不匹配: 则在cmd界面输入 chromedriver 会跳出version verison与刚刚下载好的exe不匹配,则再输入: w…...

拦截器实现 Mybatis Plus 打印含参数的 SQL 语句
1.实现拦截器 package com.sample.common.interceptor;import com.baomidou.mybatisplus.extension.plugins.inner.InnerInterceptor; import lombok.extern.slf4j.Slf4j; import org.apache.ibatis.executor.Executor; import org.apache.ibatis.mapping.BoundSql; import or…...

Oracle Subprogram即Oracle子程序
Oracle Subprogram,即Oracle子程序,是Oracle数据库中存储的过程(Procedures)和函数(Functions)的统称。这些子程序是存储在数据库中的PL/SQL代码块,用于执行特定的任务或操作。下面详细介绍Orac…...

自然语言处理实战项目30-基于RoBERTa模型的高精度的评论文本分类实战,详细代码复现可直接运行
大家好,我是微学AI,今天给大家介绍一下自然语言处理实战项目30-基于RoBERTa模型的高精度的评论文本分类实战,详细代码复现可直接运行。RoBERTa模型是由 Facebook AI Research 和 FAIR 的研究人员提出的一种改进版的 BERT 模型。RoBERTa 通过采用更大的训练数据集、动态掩码机…...
RK3588J正式发布Ubuntu桌面系统,丝滑又便捷!
本文主要介绍瑞芯微RK3588J的Ubuntu系统桌面演示,开发环境如下: U-Boot:U-Boot-2017.09 Kernel:Linux-5.10.160 Ubuntu:Ubuntu20.04.6 LinuxSDK: rk3588-linux5.10-sdk-[版本号] (基于rk3…...
基于GPT-SoVITS的API实现批量克隆声音
目标是将每一段声音通过GPT-SoVITS的API的API进行克隆,因为拼在一起的整个片段处理会造成内存或者缓存溢出。 将目录下的音频文件生成到指定目录下,然后再进行拼接。 通过AI工具箱生成的数据文件是这样的结构,temp目录下是没个片段生成的部分,connect_是正常拼接的音频文件…...
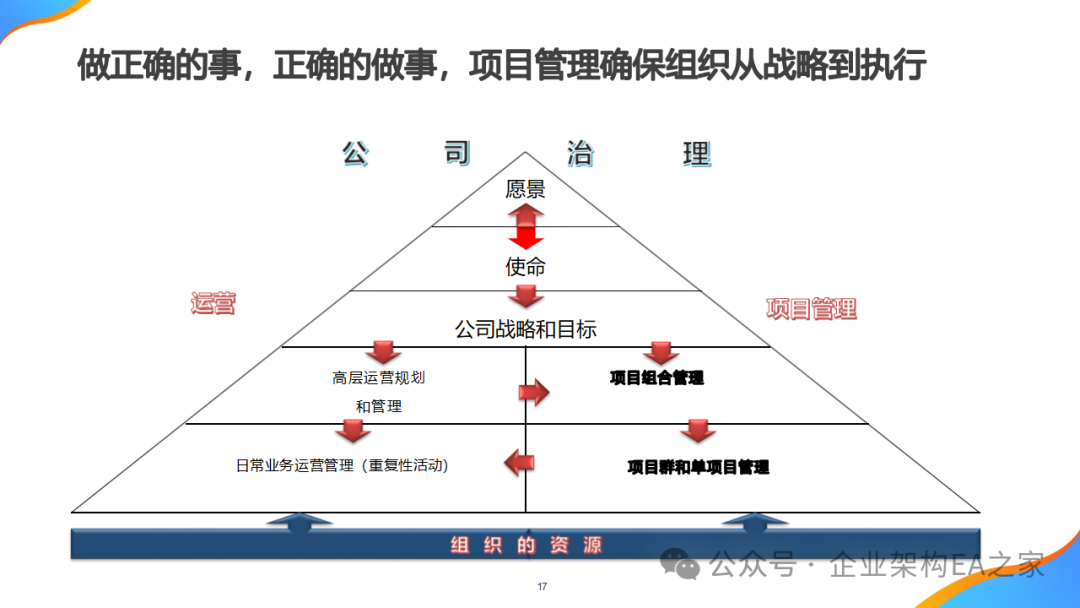
详解华为项目管理,附华为高级项目管理内训材料
(一)华为在项目管理中通过有效的沟通、灵活的组织结构、坚持不懈的努力、细致的管理和科学的考核体系,实现了持续的创新和发展。通过引进先进的管理模式,强调以客户需求为导向,华为不仅优化了技术管理和项目研发流程&a…...
脚本)
Perl(Practical Extraction and Reporting Language)脚本
Perl(Practical Extraction and Reporting Language)是一种非常灵活的脚本语言,主要用于文本处理、系统管理以及快速原型开发等领域。Perl 脚本可以用来执行一系列任务,包括文件操作、网络通信、数据处理等。 下面是一些关于编写…...

单例模式详细
文章目录 单例模式介绍八种方式1、饿汉式(静态常量)2、饿汉式(静态代码块)3、懒汉式(线程不安全)4、懒汉式(线程安全,同步方法)5、懒汉式(线程不安全…...
Unity3D 自定义窗口
Unity3D 自定义窗口的实现。 自定义窗口 Unity3D 可以通过编写代码,扩展编辑器的菜单栏和窗口。 简单的功能可以直接一个菜单按钮实现,复杂的功能就需要绘制一个窗口展示更多的信息。 编辑器扩展的脚本,需要放在 Editor 文件夹中。 菜单栏…...
dubbo:dubbo整合nacos实现服务注册中心、配置中心(二)
文章目录 0. 引言1. nacos简介及安装2. 注册中心实现3. 配置中心实现4. 源码5. 总结 0. 引言 之前我们讲解的是dubbozookeeper体系来实现微服务框架,但相对zookeeper很多企业在使用nacos, 并且nacos和dubbo都是阿里出品,所以具备一些天生的契合性&#…...

个人博客指路
Pudding 个人博客 比较懒,直接 github page 了,没国内代理加速。 欢迎大佬们,踩一踩 没做留言,觉得很鸡肋。有问题可以在本文底下评论、或者直接邮件...
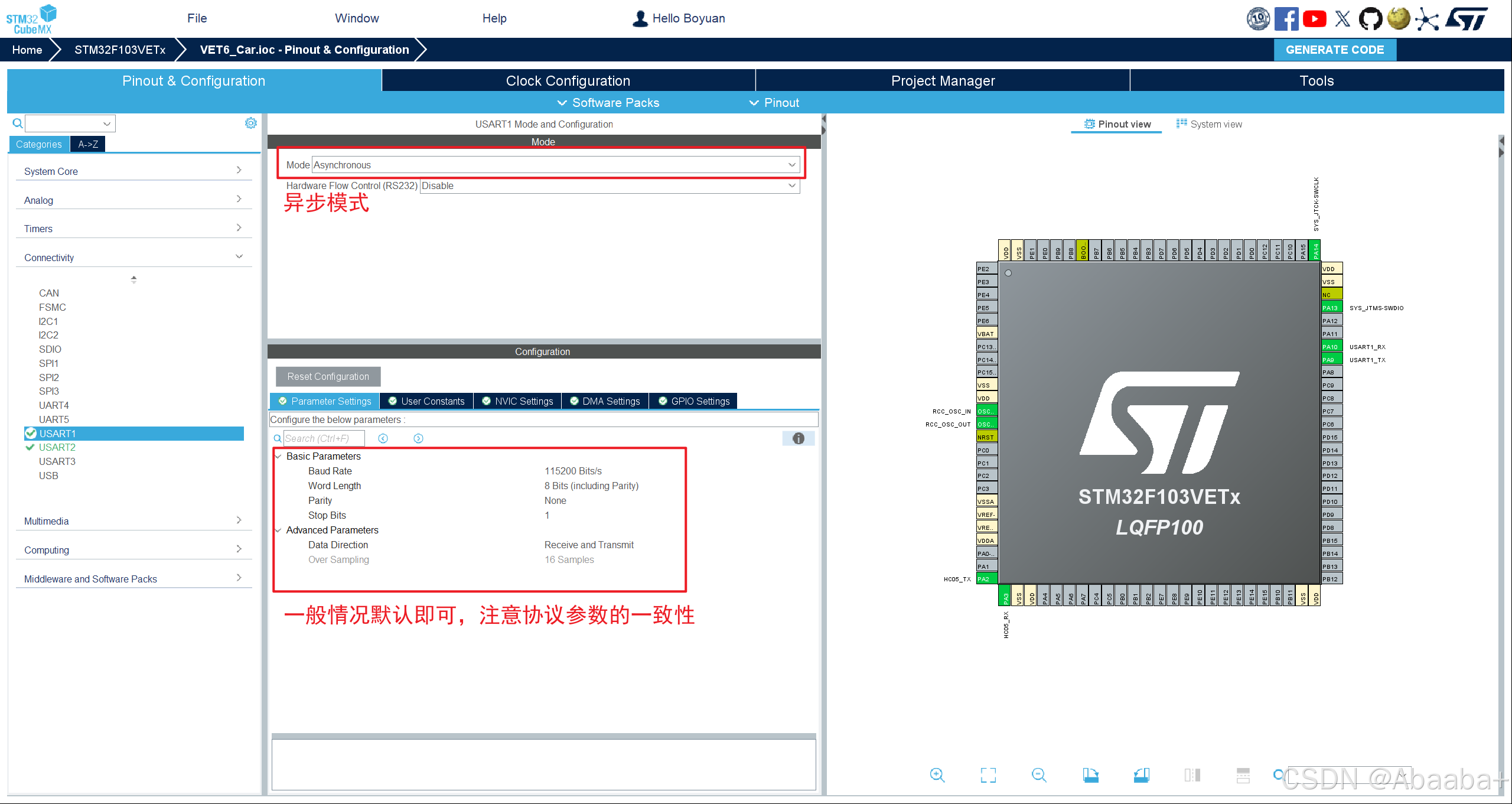
【STM32 HAL】多串口printf重定向
【STM32 HAL】多串口printf重定向 前言单串口printf重定向原理实现CubeMX配置Keil5配置 多串口printf重定向 前言 在近期项目中,作者需要 STM32 同时向上位机和手机发送数据,传统的 printf 重定向只能输出到一个串口。本文介绍如何实现 printf 同时输出…...

帆软报表,达梦数据库驱动上传失败
1、按照正常操作新建数据库连接,上传准备好的达梦驱动时,提示如图一需要修改SystemConfig.driverUpload为true才可以。 2、FineDB存储了数据决策系统中除平台属性配置以外的所有信息。详情请参见: FineDB 数据库简介。 3、因此管理员可通过…...

CSS选择器的优先级是如何确定的?有哪些方法可以提高选择器的效率?
CSS选择器的优先级是如何确定的? CSS选择器的优先级决定了当多个选择器同时应用于一个元素时,哪个选择器将最终生效。CSS选择器的优先级由多个因素决定,主要包括以下几个方面: 特殊性(Specificity) 特殊性…...
)
【MySQL】基础入门(第二篇)
1.MySQL基本数据类型 数值类型 MySQL 支持所有标准 SQL 数值数据类型。 这些类型包括严格数值数据类型(INTEGER、SMALLINT、DECIMAL 和 NUMERIC),以及近似数值数据类型(FLOAT、REAL 和 DOUBLE PRECISION)。 关键字INT是INTEGER的同义词,关键字DEC是D…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...
