3007. 价值和小于等于 K 的最大数字(24.8.21)
前言
感谢皇家笨阿宝的指导
题目
给你一个整数 k 和一个整数 x 。整数 num 的价值是它的二进制表示中在 x,2x,3x 等位置处设置位的数目(从最低有效位开始)。下面的表格包含了如何计算价值的例子。
| X | num | Binary Representation | Price |
|---|---|---|---|
| 1 | 13 | 000001101 | 3 |
| 2 | 13 | 000001101 | 1 |
| 2 | 233 | 011101001 | 3 |
| 3 | 13 | 000001101 | 1 |
| 3 | 362 | 101101010 | 2 |
num 的 累加价值 是从 1 到 num 的数字的 总 价值。如果 num 的累加价值小于或等于 k 则被认为是 廉价的。
请你返回 最大 的廉价数字。
示例 1:
输入:k = 9, x = 1
输出:6
解释:由下表所示,6 是最大的廉价数字。
| X | num | Binary Representation | Price | Accumulated Price |
|---|---|---|---|---|
| 1 | 1 | 001 | 1 | 1 |
| 1 | 2 | 010 | 1 | 2 |
| 1 | 3 | 011 | 2 | 4 |
| 1 | 4 | 100 | 1 | 5 |
| 1 | 5 | 101 | 2 | 7 |
| 1 | 6 | 110 | 2 | 9 |
| 1 | 7 | 111 | 3 | 12 |
示例 2:
输入:k = 7, x = 2
输出:9
解释:由下表所示,9 是最大的廉价数字。
| X | num | Binary Representation | Price | Accumulated Price |
|---|---|---|---|---|
| 2 | 1 | 0001 | 0 | 0 |
| 2 | 2 | 0010 | 1 | 1 |
| 2 | 3 | 0011 | 1 | 2 |
| 2 | 4 | 0100 | 0 | 2 |
| 2 | 5 | 0101 | 0 | 2 |
| 2 | 6 | 0110 | 1 | 3 |
| 2 | 7 | 0111 | 1 | 4 |
| 2 | 8 | 1000 | 1 | 5 |
| 2 | 9 | 1001 | 1 | 6 |
| 2 | 10 | 1010 | 2 | 8 |
提示:
1 <= k <= 1015
1 <= x <= 8
解题思路
见代码内
代码
class Solution {
public:long long findMaximumNumber(long long k, int x) {//二分查找的过程long long left=1,right=(k+1)<<x;while(left<right){long long mid=(left+right+1)/2;if(Sum(x,mid)>k){//如果比 k 大 说明答案在mid左边right=mid-1;}else{//如果比 k 小 说明在mid右边left=mid;}}return left;}
//求解从 1 到 num 所有整数在二进制表示下在 i 位置处设置位的数字之和
/*
规律:1 2 3 4 5 6
0: 0 0 0 0 0 0
1: 0 0 0 0 0 1
2: 0 0 0 0 1 0
3: 0 0 0 0 1 1
4: 0 0 0 1 0 0
5: 0 0 0 1 0 1
6: 0 0 0 1 1 0
7: 0 0 0 1 1 1
8: 0 0 1 0 0 0
9: 0 0 1 0 0 1此处从 0 开始列举,由于 0 的贡献值为 0 ,因此对本题无影响
数学规律:第 i 位的 0 ,1 存在周期性变化对于 i 位置 先是 2^(i-1) 个 0 后是 2^(i-1) 个 1得出周期为 2^(i-1)+2^(i-1) 即 2^i*/
//先得到二进制有几位(per):1LL<<x
//对于在一个完整周期( T )内的贡献值是: T/2
//对于在一个不完整周期( T )内的贡献值是:
// -不超过 T/2 ,贡献值为 0 ;
// -超过 T/2 ,则是超过部分个 1 ,即最后一个不完整周期到 T/2 的距离 long long Sum_per(int x,long long num){long long per=1LL<<x;long long ans=per/2*(num/per);if(num%per>=per/2){ans+=num%per-(per/2-1);}return ans;}
//是 num 的累加价值long long Sum(int x,long long num){long long ans=0;int l=64-__builtin_clzll(num);//求出数的二进制的位数(除去前导 0 )//位数不可能超过num的最高位://假设位数为:x 2x 3x 4x ...nx//则 nx<= lfor(int i=x;i<=l;i+=x){//搜索在第 i 位的累加之和ans+=Sum_per(i,num);}return ans;}
};
相关文章:
)
3007. 价值和小于等于 K 的最大数字(24.8.21)
前言 感谢皇家笨阿宝的指导 题目 给你一个整数 k 和一个整数 x 。整数 num 的价值是它的二进制表示中在 x,2x,3x 等位置处设置位的数目(从最低有效位开始)。下面的表格包含了如何计算价值的例子。 XnumBinary RepresentationPri…...

微服务 - 分布式锁的实现与处理策略
作者:逍遥Sean 简介:一个主修Java的Web网站\游戏服务器后端开发者 主页:https://blog.csdn.net/Ureliable 觉得博主文章不错的话,可以三连支持一下~ 如有疑问和建议,请私信或评论留言! 分布式锁的实现与处理…...

Catf1ag CTF Web(九)
前言 Catf1agCTF 是一个面向所有CTF(Capture The Flag)爱好者的综合训练平台,尤其适合新手学习和提升技能 。该平台由catf1ag团队打造,拥有超过200个原创题目,题目设计注重知识点的掌握,旨在帮助新手掌握C…...

QT QFileDialog 类
QFileDialog 类 QFileDialog 类 QFileDialog 是 Qt 库中的一个类,用于提供文件选择对话框, 允许用户选择文件或目录。QFileDialog 提供了多种静态方法和实例方法, 用于创建和配置文件对话框,并获取用户选择的文件或目录。 QObje…...
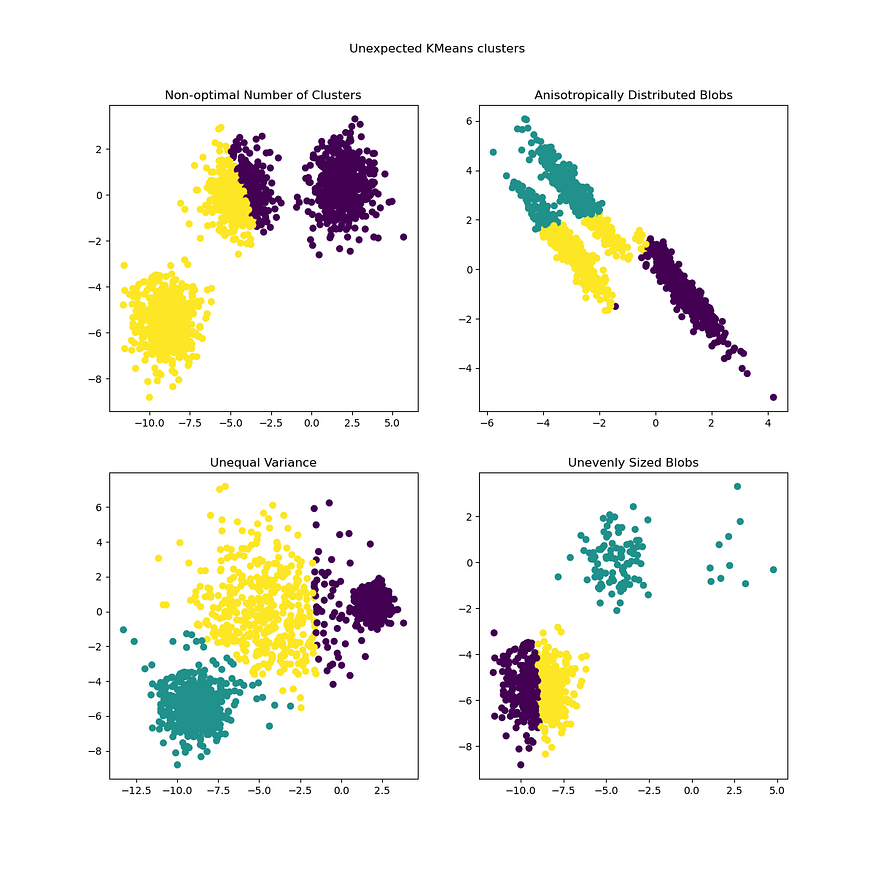
了解 K-Means 聚类的工作原理(详细指南)
一、说明 K-means 的目标是将一组观测值划分为 k 个聚类,每个观测值分配给均值(聚类中心或质心)最接近的聚类,从而充当该聚类的代表。 在本文中,我们将全面介绍 k 均值聚类(最常用的聚类方法之一࿰…...

预警先行,弯道哨兵让行车更安全
预警先行,弯道哨兵让行车更安全”这句话深刻体现了现代交通安全理念中预防为主、科技赋能的重要性。在道路交通中,尤其是复杂多变的弯道区域,交通事故的发生率往往较高,因此,采取有效的预警措施和引入先进的交通辅助设…...

预约咨询小程序搭建开发,uniapp前端,PHP语言开发
目录 前言: 一、预约小程序搭建功能介绍 二、示例代码片段 前言: 预约咨询小程序适合需付费咨询和交流的场景:比如讲师,摄影,婚庆,美发,律师,心理等等支持商家入驻支持视频、图文、线下、电话等方式在线支付咨询。 一、预约小程…...

极速文件预览!轻松部署 kkFileView 于 Docker 中!
大家好,这几天闲的难受,决定给自己找点事做。博主的项目中有个文件预览的小需求,原有方案是想将文件转换成 PDF 进行预览。本着能借鉴就绝对不自己写的原则。今天就让我们简单试用一下 kkFileView 文件预览服务,一起探索它的强大功…...

某验九宫格分类识别
注意,本文只提供学习的思路,严禁违反法律以及破坏信息系统等行为,本文只提供思路 如有侵犯,请联系作者下架 九宫格分类如下 这种就是最简单的分类识别了,用迁移学习resnet训练即可,下面来看成品 训练代码查看往期文章中就有,部分代码如下: DEVICE = torch.device(…...

未来展望:观测云技术的发展与企业业务的融合
随着技术的不断进步,观测云作为企业数据监控和分析的关键工具,其发展与企业业务的融合趋势显得尤为重要。在未来,观测云技术将如何演进,以及它将如何更深层次地与企业业务相融合,是值得我们深入探讨的问题。 首先&…...

day6JS-DOM(文档对象模型)
DOM树 DOM 操作 1. 获取元素 1.1 根据id名获取元素 document.getElementById("id名"); 案例: <body><div id"box">div盒子</div><h1>一级标题</h1><script>console.log(document.getElementById(&quo…...

MySQL列表分区分区表
什么是列表分区分区表? 列表分区是一种根据某个列的离散值将表数据分割成多个分区的分区方式。在列表分区中,每个分区都有自己的离散值集合,当插入数据时,MySQL会根据指定的列值将数据分配到相应的分区中。这种分区方式可以使得表…...

qt打包程序方法(非常好用)
1.下载 Index of /official_releases/qt-installer-framework/4.6.1 bi...

IP地址管理:优化网络布局与提升效率
在日益复杂的网络环境中,IP地址管理成为了网络管理员日常工作中不可或缺的一部分。有效的IP地址管理不仅能够优化网络布局,提升网络运行效率,还能确保网络安全和稳定性。本文将探讨IP地址管理的重要性、实施策略以及最佳实践。 一、IP地址管…...

老古董Lisp实用主义入门教程(5):好奇先生用Lisp探索Lisp
鲁莽先生什么都不管 鲁莽先生打开电脑,安装一堆东西,噼里啪啦敲了一堆代码,叽里呱啦说了一堆话,然后累了就回家睡觉了。 这可把好奇先生的兴趣勾起来,他怎么也睡不着。好奇先生打开电脑,看了看鲁莽先生留…...

linux文件——用户缓冲区——概念深度理解、IO模拟实现
前言:本篇文章主要讲解文件缓冲区。 讲解的方式是通过抛出问题, 然后通过分析问题, 将缓冲区的概念与原理一步一步地讲解。同时, 本节内容在最后一部分还会带友友们模拟实现一下c语言的printf, fprintf接口,…...

Selenium模拟鼠标滚动页面:实现自动化测试中的页面交互
Selenium模拟鼠标滚动页面:实现自动化测试中的页面交互 在进行网页自动化测试时,经常需要模拟用户的滚动行为来加载更多内容或触发页面上的某些交互。Selenium WebDriver提供了强大的工具来模拟这些用户行为,包括鼠标滚动。本文将介绍如何使…...

Eureka原理与实践:构建高效的微服务架构
Eureka原理与实践:构建高效的微服务架构 Eureka的核心原理Eureka Server:服务注册中心Eureka Client:服务提供者与服务消费者 Eureka的实践应用集成Eureka到Spring Cloud项目中创建Eureka Server创建Eureka Client(服务提供者&…...

OpenJDK 和 OracleJDK 的区别、下载方式
OpenJDK 和 OracleJDK 都是 Java 开发套件 (JDK),用于开发和运行 Java 应用程序。它们之间的主要区别如下: 许可证和使用限制: OpenJDK:由 OpenJDK 社区开发和维护,基于 GPL v2 with Classpath Exception 许可证&#…...

arthas源码刨析:arthas-core (2)
文章目录 attach JVMagent**ArthasBootstrap** arthas-core的启动可以从上一篇做参考 参考 pom,即启动是调用的 Arthas 的 main 方法 attach JVM JVM提供了 Java Attach 功能,能够让客户端与目标JVM进行通讯从而获取JVM运行时的数据,甚至可以…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
