Matlab程序练习
Part1
1.求 [100,999] 之间能被 21整除的数的个数。
程序:
主文件:main.m
clear;
start_num = 100;
end_num = 999;
div_num = 21;
res = div(start_num,end_num,div_num);
fprintf("[%d,%d]之间能被%d整除的数的个数为%d个\n",start_num,end_num,div_num,res);
函数文件:div.m
function num=div(sta,ed,divnum)num=0;for i=sta:edif mod(i,divnum)==0num = num+1;endend
end
运行截图:

2.从键盘输入一个4位的整数,按如下规则加密后输出。加密规则:每位数字都加上7,然后用和除以10的余数取代该数字;然后将第一位数与第三位数互换,第二位数与第四位数互换。
程序:
主文件:main.m
clear;
n=input('请输入一个4位整数:');
res = process(n);
fprintf("加密后的数字为:%d\n",res);
函数文件:process.m
function ennum = process(num)ennum=0;n4 = mod(num,10)+7;n3 = mod(fix(num/10),10)+7;n2 = mod(fix(num/100),10)+7;n1 = fix(num/1000)+7;n4 = mod(n4,10);n3 = mod(n3,10);n2 = mod(n2,10);n1 = mod(n1,10); ennum = n3*1000+n4*100+n1*10+n2;
end

3.一个自然数是素数,且它的数字位置经过任意对换后仍为素数,则称之为绝对素数,例如13是绝对素数,试求出所有两位绝对素数。要求:定义一个判断素数的函数文件。
程序:
主文件:main.m
clear;
abs_prime=[];
for num=10:99unit = mod(num,10);decade = fix(num/10);if isprime(num)==1 && isprime(unit*10+decade)==1abs_prime(end+1) = num;end
end
fprintf("所有的两位绝对素数为:");
disp(abs_prime);
函数文件:isprime.m
function flag=isprime(num)flag=1;for i=2:num-1if mod(num,i)==0flag=0;breakendend
end
运行截图:

4.设 f ( x ) = 1 ( x − 2 ) 2 + 0.1 + 1 ( x − 3 ) 4 + 0.01 f(x)=\frac{1}{(x-2)^2+0.1}+\frac{1}{(x-3)^4+0.01} f(x)=(x−2)2+0.11+(x−3)4+0.011,编写一个函数文件fx.m,使得调用fx时,x 可用矩阵代入,得出的 f ( x ) f(x) f(x)为同阶矩阵。
程序:
主文件:main.m
clear;
x = input('请输入x的值,可以为一个数字,也可以为一个矩阵\nx=');
disp(fx(x));
函数文件:fx.m
function matrix = fx(x)matrix = 1./((x-2).^2+0.1) + 1./((x-3).^4+0.01);
end
运行截图:

5.已知 y = f ( 40 ) f ( 30 ) + f ( 20 ) y=\frac{f(40)}{f(30)+f(20)} y=f(30)+f(20)f(40),
(1)当 f ( n ) = n + 10 l n ( n 2 + 5 ) f(n)=n+10ln(n^2+5) f(n)=n+10ln(n2+5)时, y y y 的值是多少?
(2)当 f ( n ) = 1 ∗ 2 + 2 ∗ 3 + 3 ∗ 4 + ⋯ + n ∗ ( n + 1 ) f(n)=1*2+2*3+3*4+\cdots+n*(n+1) f(n)=1∗2+2∗3+3∗4+⋯+n∗(n+1) 时, y y y的值是多少?
程序:
主文件:main.m
clear;
y1 = fx1(40)/(fx1(30)+fx1(20));
fprintf("第一问:y的值为%f\n",y1);
y2 = fx2(40)/(fx2(30)+fx2(20));
fprintf("第二问:y的值为%f\n",y2);
函数文件:
fx1.m
function num=fx1(n)num = n+10*log(n^2+5);
end
fx2.m
function num = fx2(n)num=0;for i=1:nnum = num+(i*(i+1));end
end
运行截图:

6.编写一个函数,计算 x=-5.0, -3.0, 1.0, 2.0, 2.5, 3.0, 5.0 对应的y值。
y = { x 2 + x − 6 , x < 0 且 x ≠ − 3 x 2 − 5 x + 6 , 0 ≤ x < 5 且 x ≠ 2 及 x ≠ 3 x 2 − x − 1 , 其他 y = \begin{cases} x^2+x-6, x<0且x\neq-3\\ x^2-5x+6,0\leq x<5且x\neq 2及x\neq3\\ x^2-x-1,其他 \end{cases} y=⎩ ⎨ ⎧x2+x−6,x<0且x=−3x2−5x+6,0≤x<5且x=2及x=3x2−x−1,其他
程序:
主文件:main.c
clear;
x = [-5.0,-3.0,1.0,2.0,2.5,3.0,5.0];
y = [];
for i=1:length(x)y(end+1) = fx(x(i));
end
disp(y);
函数文件:fx.m
function y=fx(x)y=0;if x<0 && x ~= -3y = x^2 + x - 6;elseif 0<=x && x<5 && x~=2 && x~=3y = x^2 - 5*x +6;elsey = x^2-x-1;end
end
运行截图:

7.编写一个函数求向量x中元素的平均值、最大值、最小值、均方根值
程序:
主文件:main.m
clear;
x = input('x=');
[meann,maxi,mini,rms] = calc(x);
fprintf("平均值为%f,最大值为%f,最小值为%f,均方根值为%f\n",meann,maxi,mini,rms);
函数文件:calc.m
function [meann,maxi,mini,rms]=calc(x)meann = mean(x);maxi = max(x);mini = min(x);N = length(x);sigama = 0;for i=1:Nsigama = sigama+x(i)^2;endrms = sqrt(1/N * sigama);
运行截图:

Part2
1.设 y = ( 0.5 + 3 sin x 1 + x 2 ) cos x y = ( 0.5 + \frac { 3 \sin x } { 1 + x ^ { 2 } } ) \cos x y=(0.5+1+x23sinx)cosx,把 x = 0 ∼ 2 π x=0 \sim 2\pi x=0∼2π 区间分为101点,绘制函数的曲线。
程序:
clear;
x = 0:2*pi/101:2*pi;
y = (0.5+(3.*sin(x))./(1+x.^2)).*cos(x);
plot(x,y,'LineWidth',2);
xticks(0:pi/2:2*pi);
xticklabels({'0','\pi/2','\pi','3\pi/2','2\pi'});
t = title('$ y=(0.5+\frac{3 \sin x}{1+x^2}) \cos x $');
set(t,'Interpreter','latex','FontSize',14);
运行截图:

2. 用不同线型和颜色在同意坐标内绘制曲线 y = 3 e x p ( − 1.5 x ) s i n ( 3 π x ) y=3exp(-1.5x)sin(3\pi x) y=3exp(−1.5x)sin(3πx)及其包络线。
程序:
clear;
x = -3*pi:pi/50:3*pi;
y = 3.*exp(-1.5.*x).*sin(3*pi.*x);
[up,lo] = envelope(y);
plot(x,y,'r');
hold on;
plot(x,up,'b--',x,lo,'b--');
t = title('$ y=3exp(-1.5x) \sin(3\pi x) $');
set(t,'Interpreter','latex','FontSize',14);
运行截图:

3.绘制 s i n x 、 s i n ( 2 x ) 、 s i n ( x 2 ) sinx、sin(2x)、sin(\frac{x}{2}) sinx、sin(2x)、sin(2x)的函数曲线并添加图形标注,自变量范围自选,标注类型自选。
程序:
clear;
x = -4*pi:pi/50:4*pi;
y1 = sin(x);
y2 = sin(2.*x);
y3 = sin(x./2);
plot(x,y1,'blue',x,y2,'red',x,y3,'green','LineWidth',1);
h = legend('$y = \sin(x)$','$y = \sin(2x)$','$y = \sin(\frac{x}{2})$','location','NorthEastOutside');
set(h,'Interpreter','latex','fontsize',14);
运行截图:

4.已知 y 1 = x 2 , y 2 = c o s ( 2 x ) , y 3 = y 1 ∗ y 2 y_1=x^2,y_2=cos(2x),y_3=y_1*y_2 y1=x2,y2=cos(2x),y3=y1∗y2,完成下列操作。
(1)在同一坐标系下用不同的颜色、线宽均设置为2绘制三条曲线,并为各条曲线加上图例;
(2)以子图(subplot)形式绘制3条曲线;
程序:
clear;
x = -4*pi:pi/50:4*pi;
y1 = x.*x;
y2 = cos(2.*x);
y3 = y1.*y2;%Request1
figure(1);
plot(x,y1,'r',x,y2,'g',x,y3,'b','linewidth',2);
h = legend('$y_{1} = x^{2}$','$y_{2} = \cos(2x)$','$y_{3} = y_{1}*y_{2}$','location','NorthEastOutside');
set(h,'Interpreter','latex','fontsize',12);%Request2
figure(2);
subplot(1,3,1);
plot(x,y1);
title('$y_{1} = x^{2}$','Interpreter','latex','fontsize',12);
subplot(1,3,2);
plot(x,y2);
title('$y_{2} = \cos(2x)$','Interpreter','latex','fontsize',12);
subplot(1,3,3);
plot(x,y3);
title('$y_{3} = y_{1}*y_{2}$','Interpreter','latex','fontsize',12);
运行截图:


5.在同一张图中绘制下面三个函数在 t ∈ [ 0 , 4 π ] t\in[0,4\pi] t∈[0,4π]的图像。 { y 1 = t y 2 = t y 3 = 4 π e − 0.1 t s i n ( t ) \begin{equation}\begin{cases}y_1=t \\ y_2=\sqrt{t} \\y_3=4\pi e^{-0.1t}sin(t) \end{cases}\end{equation} ⎩ ⎨ ⎧y1=ty2=ty3=4πe−0.1tsin(t)
程序:
clear;
t = 0:pi/50:4*pi;
y1 = t;
y2 = sqrt(t);
y3 = 4*pi*exp(-0.1.*t).*sin(t);
plot(t,y1,t,y2,t,y3);
legend('$ y = t $','$y = \sqrt{t}$','$y = 4\pi e^{-0.1t} sin(t)$','interpreter','latex','location','NorthEastOutside');
xticks(0:pi/2:4*pi);
xticklabels({'0','\pi /2','\pi','3\pi/2','2\pi','5\pi /2','3\pi','7\pi /2','4\pi'});
运行截图:

6.创建指数函数rexp,绘制指数信号 y = A ∗ e x p ( α ∗ t ) y=A*exp(\alpha*t) y=A∗exp(α∗t),在三种情况下 ( ( 1 ) α = 0.5 , ( 2 ) α = 0 , ( 3 ) α = − 0.5 (1)\alpha=0.5,(2)\alpha = 0,(3)\alpha=-0.5 (1)α=0.5,(2)α=0,(3)α=−0.5 )的时域波形,其中A自赋值,时间区间都是[-3,3]。
程序:
主文件:main.m
clear;
%rexp()函数传入两个参数 A 和 α
A = input('A=');
x = -3:1/50:3;
y1 = rexp(A,0.5);
y2 = rexp(A,0);
y3 = rexp(A,-0.5);
plot(x,y1,x,y2,x,y3);
h = legend('$\alpha = 0.5$','$\alpha = 0$','$\alpha = -0.5$','location','NorthEastOutside');
set(h,'Interpreter','latex','fontsize',12);
title(sprintf('A=%.2f',A));
函数文件:div.m
function y=fx7(x)y=[];for i=1:length(x)if x(i)<=0y(end+1)=sin(x(i));elseif 0<=x(i) & x(i)<=3y(end+1)=x(i);elsey(end+1)=-x(i)+6;endend
运行截图:

7.编写程序,选择合适的步距,绘制下面函数在区间[-6,6]中的图像。函数用function写出来,主程序里给出区间,并画图。KaTeX parse error: {equation} can be used only in display mode.
程序:
clear;
x = -6:1/50:6;
y = fx7(x);
plot(x,y);
text(-5.8,0,'$y=sin(x),x\leq0$ ','interpreter','latex','fontsize',10);
text(0.1,1,'$y=x,0<x\leq3$ ','interpreter','latex','fontsize',10);
text(3.1,0,'$y=-x+6,x\geq3$ ','interpreter','latex','fontsize',10);
运行截图:

8.利用plot3绘制下列三维图形,并对图形进行相关的辅助说明。
(1)KaTeX parse error: {equation} can be used only in display mode. (2) KaTeX parse error: {equation} can be used only in display mode.
程序:
程序:
clear;
t = -20*pi:pi/50:20*pi;
x1 = cos(t);
y1 = sin(t);
z1 = t;
%Request1
figure(1);
plot3(x1,y1,z1);
title('x=cost ; y=sint; z=t','FontSize',12);%Request2
t = 0:pi/50:2*pi;
x2 = (2+cos(t./2)).*cos(t);
y2 = (2+cos(t./2)).*sin(t);
z2 = sin(t./2);
figure(2);
plot3(x2,y2,z2);
title({'$x=(2+cos\frac{t}{2})cost$', '$y=(2+cos\frac{t}{2})sint,0\leq t \leq 2\pi$', '$z=sin\frac{t}{2}$'},'interpreter','latex');运行截图:


9.用mesh和surf函数,绘制方程 z = x 2 10 + y 2 10 z=\frac{x^2}{10}+\frac{y^2}{10} z=10x2+10y2 和 z = − x 2 10 + y 2 10 z=-\frac{x^2}{10}+\frac{y^2}{10} z=−10x2+10y2所表示的三维空间曲面,x和y的取值范围设为[-3,3]。
程序:
clear;
x = -3:1/10:3;
y = -3:1/10:3;
[x,y] = meshgrid(x,y);
z1 = (x.*x)/10 + (y.*y)/10;
z2 = -(x.*x)/10 + (y.*y)/10;figure(1);
subplot(1,2,1);
mesh(x,y,z1);
subplot(1,2,2);
surf(x,y,z1);
sgtitle('$z=\frac{x^2}{10}+\frac{y^2}{10}$','Interpreter','latex');figure(2);
subplot(1,2,1);
mesh(x,y,z2);
subplot(1,2,2);
surf(x,y,z2);
sgtitle('$z=-\frac{x^2}{10}+\frac{y^2}{10}$','Interpreter','latex');
运行截图:


相关文章:

Matlab程序练习
Part1 1.求 [100,999] 之间能被 21整除的数的个数。 程序: 主文件:main.m clear; start_num 100; end_num 999; div_num 21; res div(start_num,end_num,div_num); fprintf("[%d,%d]之间能被%d整除的数的个数为%d个\n",start_num,end_…...

cesium可不可以改变影像底图颜色,如何给地球底图影像添加一层滤镜蒙版?
废话:你的球是不是很丑?是不是没有科技感?是不是没有好看的影像? 因果: 因:客户问,底图可不可以改变颜色,想让球更漂亮一些。 答:可以改变影像饱和度,透明度…...

MyBatis-MappedStatement什么时候生成?QueryWrapper如何做到动态生成了SQL?
通过XML配置的MappedStatement 这部分MappedStatement主要是由MybatisXMLMapperBuilder进行解析,核心逻辑如下: 通过注解配置的MappedStatement 核心逻辑就在这个里面了: 继承BaseMapper的MappedStatement 我们看看这个类,里…...

Netty系列-2 NioServerSocketChannel和NioSocketChannel介绍
背景 本文介绍Netty的通道组件NioServerSocketChannel和NioSocketChannel,从源码的角度介绍其实现原理。 1.NioServerSocketChannel Netty本质是对NIO的封装和增强,因此Netty框架中必然包含了对于ServerSocketChannel的构建、配置以及向选择器注册&am…...
智能客服的四大优势,提升企业服务效率
在这个信息化快速发展的时代,客户服务的重要性越来越凸显。传统的客服方式已经无法满足企业日益增长的服务需求,于是智能客服服务应运而生。智能客服服务不仅改变了企业与客户的互动方式,还提高了服务效率和客户满意度。本文将深入探讨智能客…...

AutoGPT开源项目解读
AutoGPT开源项目解读 (qq.com) AutoGPT旨在创建一个自动化的自我改进系统,能够自主执行和学习各种任务 项目基本信息 首先阅读项目的README.md,下述代理和智能体两个名词可互换 项目简介:一个创建和运行智能体的工具,这些智能体…...

Linux离线安装fontconfig
Linux离线下载yum包,安装字体库 一、下载安装包 以CentOS Linux release 7.9.2009下载fontconfig的rpm包的为例 http://mirror.centos.org/centos/7/按提示跳转历史库 找到对应版本的centos https://vault.centos.org/7.9.2009/os/x86_64/Packages/在Packages目…...

海山数据库(He3DB)+AI:(一)神经网络基础
文章目录 1 引言2 基本结构2.1 神经元2.2 模型结构 3 训练过程3.1 损失函数3.2 反向传播3.3 基于梯度的优化算法 4 总结 1 引言 神经网络可以被视为一个万能的拟合器,通过深层的隐藏层实现输入数据到输出结果的映射。神经网络的思想源于对大脑的模拟,在…...
)
CSS中选择器有哪些?(史上最全选择器)
CSS选择器是用来选择和应用样式到HTML元素上的工具。以下是所有主要的CSS选择器的详细分类和描述: 1. 基本选择器 通配符选择器 (*):选择所有元素。例如,* { color: red; } 会将所有元素的文字颜色设置为红色。元素选择器:选择指…...
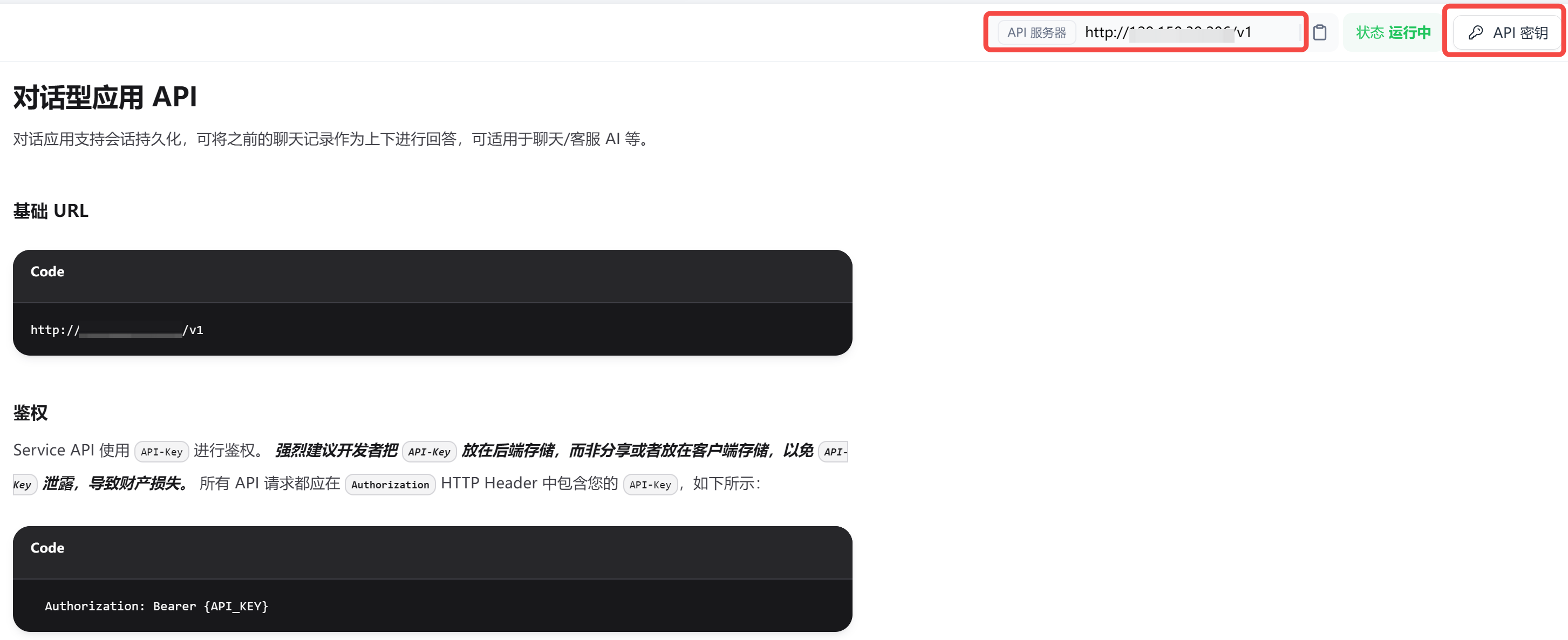
本地部署 AI 智能体,Dify 搭建保姆级教程(下):知识库 RAG + API 调用,我捏了一个红楼解读大师
话接上篇: 本地部署 AI 智能体,Dify 搭建保姆级教程(上):工作流 Agent,把 AI 接入个人微信 相信大家已经在本地搭建好 Dify 了。 今日分享,继续介绍 Dify 的另外两项重要功能: 知…...

HarmonyOS应用开发者高级认证,Next版本发布后最新题库 - 答案纯享版
这篇文章是高级题库答案纯享版,只有需要选择的选项。如果需要查看所有选项,可以点击下方链接跳转。以考代学,还是推荐点击下方链接,查看完整的题库,边看边学习鸿蒙应用开发。此题库已更新完毕,笔者将不继续…...

基于PHP的文件包含介绍
引言:在实际开发过程中,经常会遇到部分模块功能需要重复使用的情况,比如数据库的增删改查,文件包含通过将需要重复使用的功能模块代码引入其他文件的内容,实现重用代码、分离配置等。然而,如果文件包含操作…...

K7系列FPGA多重启动(Multiboot)
Xilinx 家的 FPGA 支持多重启动功能(Multiboot),即可以从多个 bin 文件中进行选择性加载,从而实现对系统的动态更新,或系统功能的动态调整。 这一过程可以通过嵌入在 bit 文件里的 IPROG 命令实现上电后的自动加载。而…...

关于武汉芯景科技有限公司的RS232通信接口芯片XJ3243EEUI开发指南(兼容MAX3243EEUI)
一、芯片引脚介绍 1.芯片引脚 2.引脚描述 二、典型应用电路 三、功能描述 1.Transmitter 通过T1,T2可以将TTL电平转换为RS232电平 2.Receiver 通过R1,R2可以将RS232电平转换为TTL电平 3.工作模式控制 4.INVALID引脚...
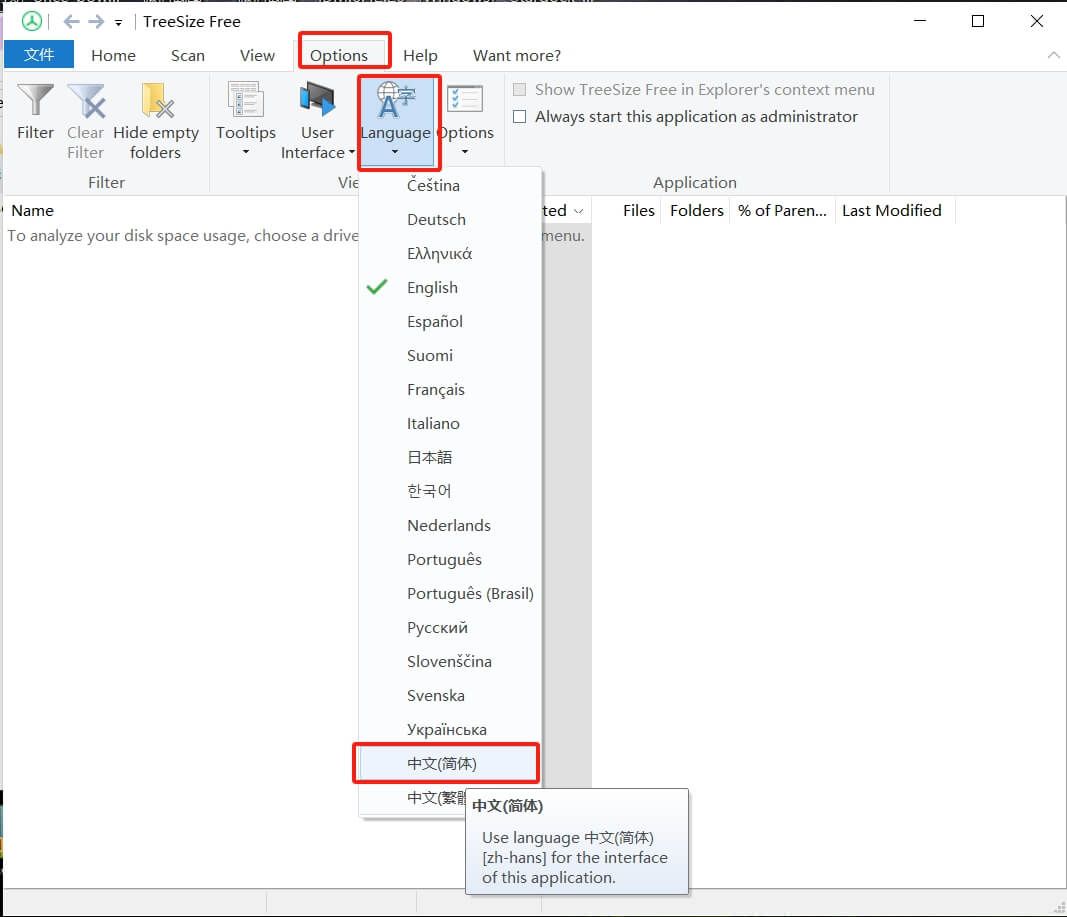
TreeSize Free:你的免费磁盘空间管理专家
TreeSize Free是一款专为Windows用户设计的磁盘空间分析工具。它能够帮助用户快速识别并管理那些占用大量空间的文件夹和文件。 功能亮点 快速扫描:TreeSize Free能够迅速扫描整个磁盘卷,展示所有文件夹及其子文件夹的大小,甚至可以细化到单…...

python办公自动化:初识`python-docx`
1.1 什么是python-docx python-docx是一个用于在Python中创建和操作Word文档的库。它提供了一组简洁的API,让开发者可以轻松地生成、修改、和读取Microsoft Word (.docx)文件,而不需要安装Microsoft Office。这使得python-docx成为办公自动化、报告生成…...

LeetCode 算法:划分字母区间 c++
原题链接🔗:划分字母区间难度:中等⭐️⭐️ 题目 给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。 注意,划分结果需要满足:将所有划分结果按顺序连接&#…...

PMP备考指南:策略、时间安排与心得分享
准备和时间安排,我是工作的时间把它顺便考了,大约花了一个月左右时间备考,前面的时间都在筹办婚礼,根本没时间,最后一个月都差点想放弃了,但想想还是冲一把就没有选择延考。 干货见下: ▌&…...

CentOS上通过frp实现HTTPS访问内网
要在CentOS上通过frp实现HTTPS访问内网,你需要按照以下步骤操作: 在外网服务器上安装frps(frp服务端)。 在外网服务器上配置frps,编辑配置文件frps.ini。 在frps服务器上启动frps服务。 在内网服务器上安装frpc&…...

短视频SDK解决方案,高效集成,助力商业变现
美摄科技,作为业界领先的多媒体技术服务商,其全面升级的短视频SDK解决方案,旨在为开发者与内容创作者提供一站式、高效能的创作工具,让每一个灵感都能瞬间转化为触动人心的视频作品。 【一站式解决方案,重塑短视频创作…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...
