探索C++编程技巧:计算两个字符串的最长公共子串
探索C++编程技巧:计算两个字符串的最长公共子串
在C++面试中,考官通常会关注候选人的编程能力、问题解决能力以及对C++语言特性的理解。一个常见且经典的问题是计算两个字符串的最长公共子串(Longest Common Substring, LCS)。本文将详细介绍如何编写一个函数来解决这个问题,并深入探讨相关的编程技巧和优化方法。
目录
- 引言
- 问题描述
- 解决思路
- 实现步骤
- 基础实现
- 动态规划优化
- 代码示例
- 复杂度分析
- 总结
1. 引言
最长公共子串问题是字符串处理中的一个经典问题,广泛应用于文本编辑、DNA序列比对等领域。通过解决这个问题,考官可以评估候选人对字符串操作、动态规划等算法的理解和应用能力。
2. 问题描述
给定两个字符串str1和str2,找出它们的最长公共子串。公共子串是指两个字符串中连续出现的相同字符序列。要求返回最长公共子串的长度及其内容。
3. 解决思路
解决最长公共子串问题的常用方法是动态规划。动态规划通过构建一个二维数组来记录子问题的解,从而避免重复计算,提高算法效率。
4. 实现步骤
基础实现
首先,我们可以通过暴力枚举的方法来解决这个问题。虽然这种方法简单直观,但时间复杂度较高,不适合处理大规模数据。
#include <iostream>
#include <string>
#include <algorithm>std::string longestCommonSubstring(const std::string& str1, const std::string& str2) {int maxLength = 0;std::string longestSubstr;for (size_t i = 0; i < str1.size(); ++i) {for (size_t j = 0; j < str2.size(); ++j) {int length = 0;while (i + length < str1.size() && j + length < str2.size() && str1[i + length] == str2[j + length]) {++length;}if (length > maxLength) {maxLength = length;longestSubstr = str1.substr(i, length);}}}return longestSubstr;
}int main() {std::string str1 = "abcdef";std::string str2 = "zabcf";std::string result = longestCommonSubstring(str1, str2);std::cout << "Longest Common Substring: " << result << std::endl;return 0;
}
动态规划优化
为了提高效率,我们可以使用动态规划来优化上述算法。动态规划通过构建一个二维数组dp,其中dp[i][j]表示以str1[i-1]和str2[j-1]结尾的最长公共子串的长度。
#include <iostream>
#include <string>
#include <vector>std::string longestCommonSubstring(const std::string& str1, const std::string& str2) {int m = str1.size();int n = str2.size();std::vector<std::vector<int>> dp(m + 1, std::vector<int>(n + 1, 0));int maxLength = 0;int endIndex = 0;for (int i = 1; i <= m; ++i) {for (int j = 1; j <= n; ++j) {if (str1[i - 1] == str2[j - 1]) {dp[i][j] = dp[i - 1][j - 1] + 1;if (dp[i][j] > maxLength) {maxLength = dp[i][j];endIndex = i - 1;}}}}return str1.substr(endIndex - maxLength + 1, maxLength);
}int main() {std::string str1 = "abcdef";std::string str2 = "zabcf";std::string result = longestCommonSubstring(str1, str2);std::cout << "Longest Common Substring: " << result << std::endl;return 0;
}
5. 复杂度分析
- 时间复杂度:动态规划算法的时间复杂度为
O(m * n),其中m和n分别是两个字符串的长度。相比于暴力枚举的O(m * n * min(m, n)),动态规划显著提高了效率。 - 空间复杂度:动态规划算法的空间复杂度为
O(m * n),用于存储二维数组dp。在实际应用中,可以通过滚动数组优化空间复杂度至O(min(m, n))。
6. 总结
通过本文的介绍,我们详细讲解了如何编写一个函数来计算两个字符串的最长公共子串。我们首先实现了一个基础的暴力枚举算法,然后通过动态规划进行了优化。动态规划不仅提高了算法效率,还展示了其在解决复杂问题中的强大能力。
希望本文对你有所帮助,能够在实际项目和面试中应用这些编程技巧。如果你有任何问题或建议,欢迎在评论区留言讨论!
相关文章:

探索C++编程技巧:计算两个字符串的最长公共子串
探索C编程技巧:计算两个字符串的最长公共子串 在C面试中,考官通常会关注候选人的编程能力、问题解决能力以及对C语言特性的理解。一个常见且经典的问题是计算两个字符串的最长公共子串(Longest Common Substring, LCS)。本文将详…...

等保2.0--安全计算环境--TiDB数据库
在使用本博客提供的学习笔记及相关内容时,请注意以下免责声明:信息准确性:本博客的内容是基于作者的个人理解和经验,尽力确保信息的准确性和时效性,但不保证所有信息都完全正确或最新。非专业建议:博客中的内容仅供参考,不能替代专业人士的意见和建议。在做出任何重要决…...

【unity实战】使用新版输入系统Input System+Rigidbody实现第三人称人物控制器(附项目源码)
最终效果 前言 使用CharacterController实现3d角色控制器,之前已经做过很多了: 【unity小技巧】unity最完美的CharacterController 3d角色控制器,实现移动、跳跃、下蹲、奔跑、上下坡、物理碰撞效果,复制粘贴即用 【unity实战】C…...
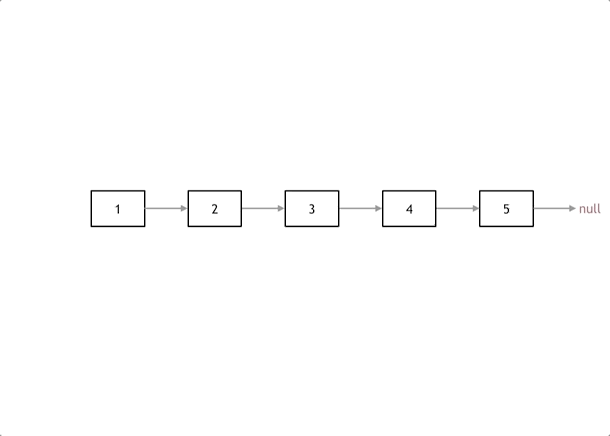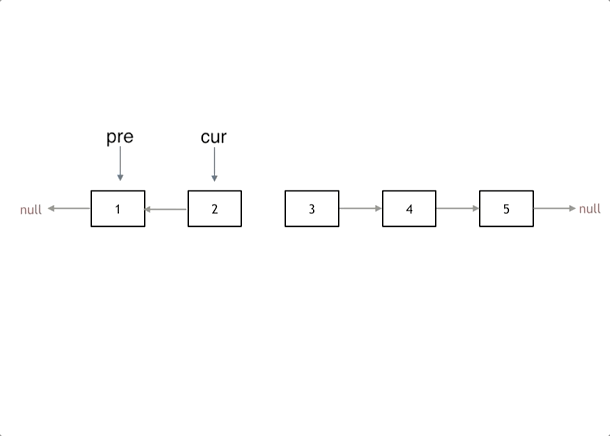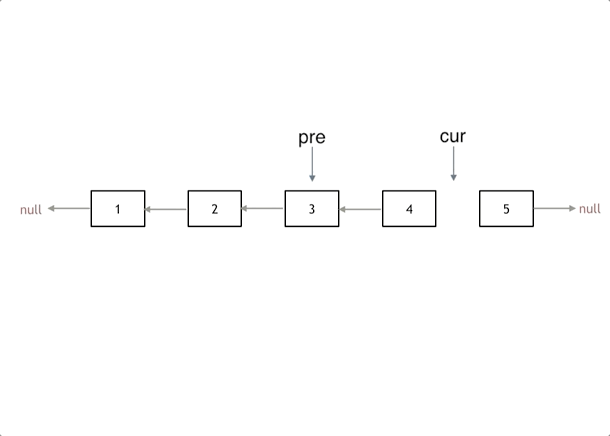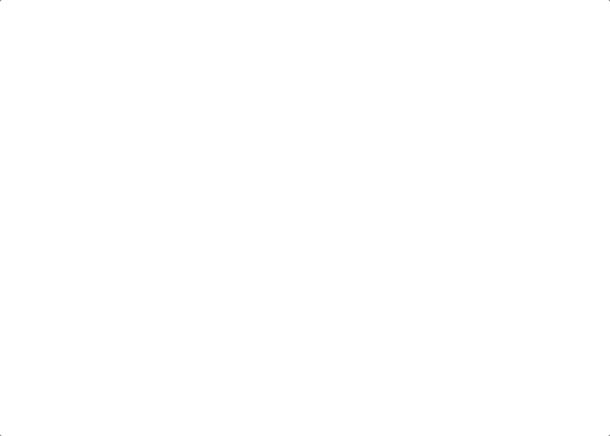
代码随想录算法训练营Day03 | 链表理论基础、203.移除链表元素 、707.设计链表、206.反转链表
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 链表理论基础203.移除链表元素思路与重点 707.设计链表思路与重点 206.反转链表思路与重点 链表理论基础 C/C的定义链表节点方式: // 单链表 struct L…...
 不常用属性)
【总结】CSS(SCSS) 不常用属性
1、设置 antd Meta 组件中 title 过长自动换行: .ant-card-meta-title {white-space: normal; /* 允许文本换行 */overflow: visible; /* 防止内容被截断 */text-overflow: clip; /* 禁用文本省略号 */} 2、选择器书写: .QR {&:hover {}} 3、设置文…...
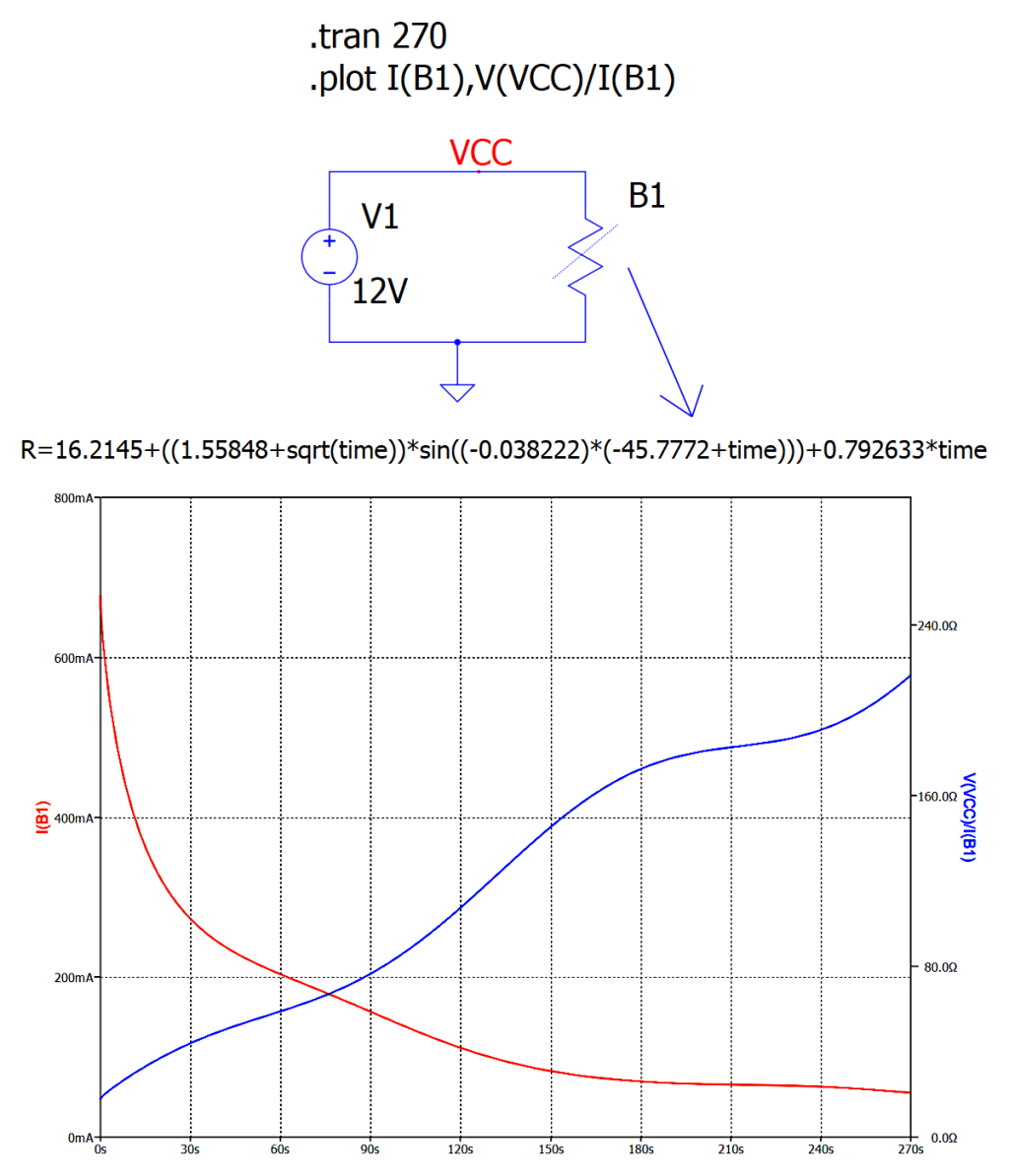
电位计的模拟
该电位计的内部电阻在 270 范围内以“几乎”线性的方式从大约 15 欧姆变化到 220 欧姆。该设备的电流和电阻特性如下表所示: 计算曲线拟合以插入电位计欧姆电阻的非线性趋势非常简单。电位曲线如下: R16.2145((1.55848sqrt(x))*sin((-0.038222)*(-45.77…...

OSI七层网络协议
1、OSI各层数据的名称 7-5,应用层、表示层、会话层都叫做协议数据单元(PDU, Protocol Data Unit)。 4,传输层叫数据段(Segment)。 3,网络层叫数据包/报文(Packet)。 2,数据链路层叫数据帧(Frame)。 1,物理层叫比特流(…...
U盘提示需要格式化才能使用怎么办?教你轻松应对
U盘作为一种便捷的数据存储设备,广泛应用于日常工作和生活中。然而,有时我们会遇到U盘插入电脑后提示需要格式化才能使用的情况,这让人倍感焦虑,因为格式化往往意味着数据丢失。不过,在采取极端措施之前,我…...

Atom编辑器:曾经的效率提升利器,终将被新技术取代
Atom编辑器:曾经的效率提升利器,终将被新技术取代 哪个编程工具让你的工作效率翻倍 ? 那么对我来说答案是 Atom。 作为一名Python开发者,我一直依赖Atom编辑器进行日常编程工作。在漫长的开发旅程中,Atom成为了我代码…...

立创商城9.9免邮活动开始啦!
从9月2日起,立创商城推出免邮活动,每月在领券中心>精选专区领取免邮券,即可享受满9.9元使用免邮券服务。 未注册的用户,可扫描下方二维码注册哦~...

图形几何-如何将凹多边形分解成若干个凸多边形
凹多边形的概念 凹多边形是指至少有一个内角大于180度的多边形。与之相对,凸多边形的所有内角均小于或等于180度,且任意两点之间的连线都完全位于多边形内部。将凹多边形分解成若干个凸多边形是计算几何中的一个重要问题。 分解原理 将凹多边形分解为凸…...

一个php快速项目搭建框架源码,带一键CURD等功能
介绍: 框架易于功能扩展,代码维护,方便二次开发,帮助开发者简单高效降低二次开发成本,满足专注业务深度开发的需求。 百度网盘下载 图片:...

STM32基础篇:RTC × Unix时间戳 × BKP
Unix时间戳 最早是在Unix系统使用的,之后很多由Unix演变而来的系统也都继承了Unix时间戳的规定。目前,Linux、Windows、安卓这些系统,其底层的计时系统都是使用Unix时间戳。 Uinx时间戳(Unix Timestamp)定义为从UTC/…...
Recyclerview部分列固定部分列滑动学习备忘
安卓使用RecyclerViewHorizontalScrollView 实现Item整体横向滑动 - 简书 (jianshu.com)https://www.jianshu.com/p/75bba86dd61c Android仿同花顺自选股列表控件介绍 RecyclerView的开发中,我们通常会遇到一行显示不下内容的情况,产品会 - 掘金 (jueji…...

【Python】路径(绝对路径、相对路径,当前工作目录),模块搜索路径(添加),Python安装路径,补充:cmd(命令行窗口)运行Python文件
Python中经常用到路径,比如:文件路径(读取文件,保存文件等),模块搜索路径(导入其他模块),Python安装路径。 而路径有两种:绝对路径,相对路径。在…...

Oceanbase 透明加密TDE
官方文档:数据库透明加密概述-V4.3.2-OceanBase 数据库文档-分布式数据库使用文档 OceanBase 数据库社区版暂不支持数据透明加密。 数据存储加密是指对数据和 Clog 等保存在磁盘中的数据进行无感知的加密,即透明加密(简称 TDE)。…...

图像去噪实验:基于全变分(TV)模型的MATLAB实现
一、背景 全变分模型在图像处理领域中被广泛用于去除噪声,同时保持图像边缘的清晰度。 二、实验步骤 图像的读取、噪声添加、去噪处理以及结果的显示。 三、实验仿真结果图 四、结论 全变分模型是一种有效的图像去噪方法,它能够在去除噪声的同时&#…...

97.WEB渗透测试-信息收集-Google语法(11)
免责声明:内容仅供学习参考,请合法利用知识,禁止进行违法犯罪活动! 内容参考于: 易锦网校会员专享课 上一个内容:96.WEB渗透测试-信息收集-Google语法(10) 2 、找上传类漏洞地址&…...

连锁美业门店如何寻找精准客户?美业SaaS拓客系统管理系统源码
连锁美业门店要寻找精准客户,可以采取多种方法结合现实因素进行推广和营销。以下是博弈美业系统给出的一些建议: 1.定位目标客户群体: 首先,门店需要确定目标客户是谁。这可能包括年龄、性别、收入水平、生活方式以及消费习惯等…...

RK3588开发板利用udp发送和接收数据
目录 1 send.cpp 2 receive.cpp 3 编译运行 4 测试 1 send.cpp #include <iostream> #include <string> #include <cstring> #include <unistd.h> #include <sys/socket.h> #include <netinet/in.h> #include <arpa/inet.h> //…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...
