【算法基础】一篇文章彻底弄懂Dijkstra算法|多图解+代码详解

- 博主简介:努力学习的大一在校计算机专业学生,热爱学习和创作。目前在学习和分享:算法、数据结构、Java等相关知识。
- 博主主页: @是瑶瑶子啦
- 所属专栏: 算法 ;该专栏专注于蓝桥杯和ACM等算法竞赛🔥
- 近期目标:写好专栏的每一篇文章

目录
- 一、简介
- 二、基本思想策略
- 三、代码实现
- 输入格式
- 输出格式
- 数据范围
- 3.1伪代码详解
- 3.2源代码详解
- 3.4:数据结构优化
- 3.3:算法分析
- 四、使用小根堆来优化Dijkstra算法
- 五、深入和反思
一、简介
Dijkstra算法适用于最短路问题中,单源最短路(只有一个起点),并且每条边的权重都是正数的情况
二、基本思想策略
首先假定源点为u(就是起点),顶点集合V被划分为两部分:集合 S 和 V-S。 初始时S中仅含有源点u,其中S中的顶点到源点的最短路径已经确定。
集合S 和V-S中所包含的顶点到源点的最短路径的长度待定,称从源点出发只经过S中的点到达V-S中的点的路径为特殊路径(不一定是最短的)
并用dist[]记录当前每个顶点对应的最短特殊路径长度。
红色顶点是S集合中,均已经确定最短路径的点,而绿色的是V-S集合中没有确定该顶点到源点最短路径的点。我们可以看到只经过S中的点到绿色点有两条特殊路径:
15+20和20+10,但是只有一条最短路径:15+20,那么绿色点就当前情况来看,可以暂时把它的dist[i]更新为25,但是一定是最短特殊路径吗?不一定,为什么呢?我们接下来往下看
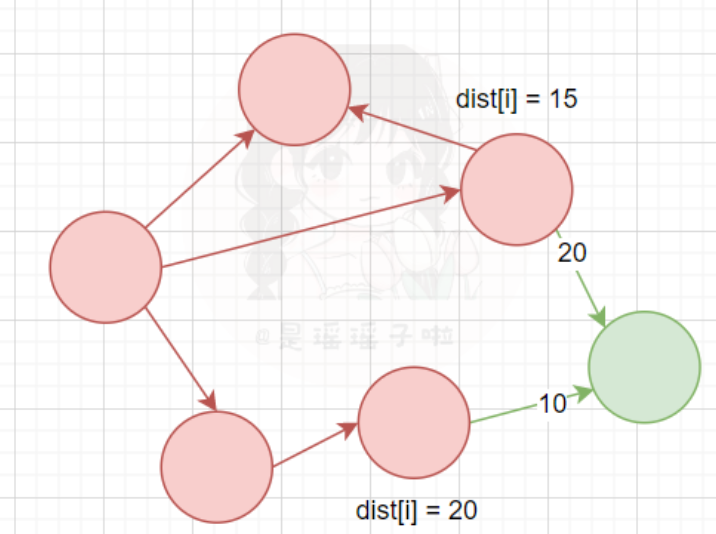
可以看到,V-S集合中假设存在一点T,经过这点到目的点的距离,很有可能是目的点真正的dist!
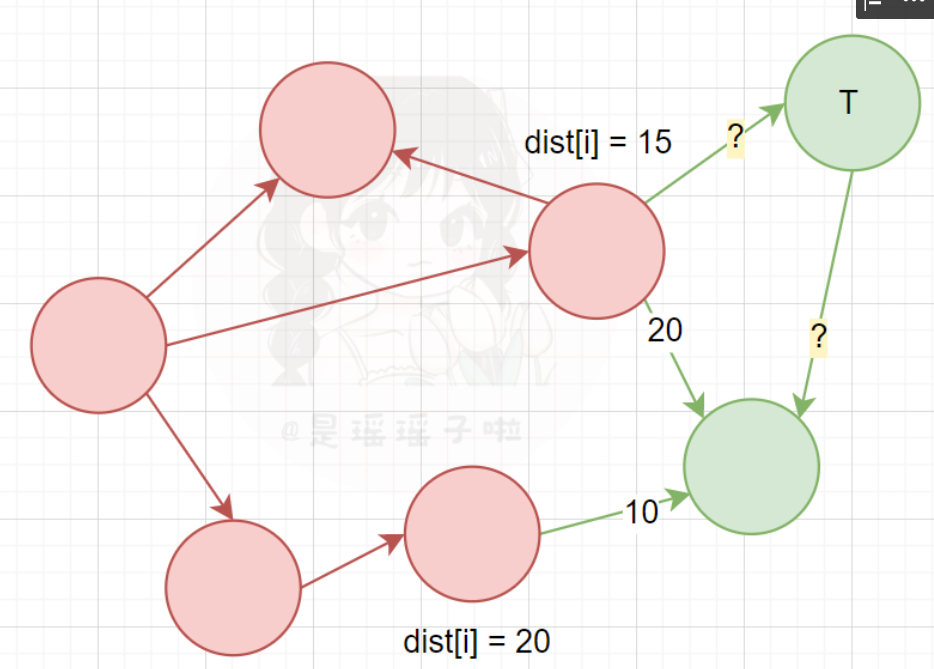
可能这里可能有点晕,没错。上面只是一个大概的介绍,我们接下来彻底揭开它的神秘面纱。
选择特殊路径长度最短的路径,将其连接的V-S中的顶点加入到集合S中,同时更新数组dist[](核心)。一旦S包含了所有顶点,dist[]就是从源到所有其他顶点的最短路径长度。
数据结构: h[N],e[M],ne[M],w[M]构建带权重的邻接表,来存储图;int dist[N];//dist 数组保存源点到其余各个节点的距离
(1)初始化。令集合S={0},对于集合V-S中的所有顶点x{1,2,3…n};初始化dist数组memset(dist, 0x3f, sizeof(dist));//dist 数组的各个元素为无穷大,
(2)找最小。在集合V-S中依照贪心策略来寻找使得dist[j]具有最小值的顶点t,即dist[t]=min,则顶点t就是集合V-S中距离源点u最近的顶点。
(3)加入S战队。将顶点t加入集合S,同时更新V-S
(4)借东风。在(2)中已近找到了源点到t的最短路径,那么对集合V-S中所有与顶点t相邻的顶点j,都可以借助t走捷径。
如果dist[i] = min(dist[i], dist[t] + w[j]);//更新 dist[j],转(2)。
光凭这个好像是这么回事,但是细节值得推敲。这个题的本质还是贪心。
比如只看刚刚的文字,不仔细分析,你能不能解决我开头提出的那个问题?
为什么这么说呢。因为在目前(局部情况)来看,确实找到最短特殊路径了,竟然就直接加入S战队,不太可取,就像我开头提出的,在V-S集合中,万一存在一个点,经过这个点再到目的点,很有可能才是真正的最短距离。
那为什么这个算法是可取的呢?
巧就巧在,最外层循环,遍历了整个顶点,并且并不是说,一旦该顶点加入了S战队,它的dist就不能变了,相反,它在实时更新!。当循环遍历到绿色顶点T时,会更新与它相连节点的dist。
不知道有没有get到我的意思,虽然我没有用公式啥的去推导,我个人也非常讨厌那种不人性化的方式,更喜欢用一种形象的,意会的方式去理解。
综上,由局部最优,到全局最优,这种贪心的策略,完全可以保证全部遍历和循环后,dist[]数组中存的就是该点到源点的最短距离!!!(上面是我个人的理解,欢迎一起讨论交流和学习捏!)
三、代码实现
这里是AcWing 849.Dijkstra求最短路 I模板题目
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1。
数据范围
1≤n≤500,
1≤m≤105,
图中涉及边长均不超过10000。
3.1伪代码详解
int dist[N],state[N];
dist[1] = 0,state = 1;//把源点加入S集合
for (i : 1~n)
{1),t<-找最小,找到只经过S中的点到V-S集合中某一点,距离最小的那个V-S中的那个点2),state[t] = 1;将t加入到S战队3),更新与t顶点相邻点的dist}
3.2源代码详解
#include<iostream>
#include<cstring>
#include<algorithm>using namespace std;//N是顶点数,M是边数
const int N =510,M = 100010;
int h[N],e[M],ne[M],w[M],idx;//邻接表存储图,w[M]存储边的权重
int state[N];//state记录是否找到了源点到该节点的最短距离
int dist[N];//dist保存源点到其余各个顶点的最短特殊距离
int n,m;//图的顶点数和边数void add(int a,int b,int c)//插入边,并给每个边赋值权重
{e[idx] = b, w[idx] = c, ne[idx] = h[a],h[a] = idx++;
}
//key:核心和关键部分!!!
void Dijkstra()
{memset(dist,0x3f,sizeof(dist));// 1)初始化dist数组dist[1] = 0;//源点到源点的距离当然是0for (int i = 0; i < n; i++)//对n个顶点进行n次遍历(一开始V-S集合为n个元素,S集合是0个,肯定是遍历n次,才能完全遍历完{int t = -1;//t存储当前这次遍历到的V-S集合中的点,该点当前局部情况距离源点距离最小的那个点//2)在V-S中 找最小for (int j = 1; j <= n; j++){if(!state[j] && (t == -1 || dist[j] < dist[t]))t = j;}state[t] = 1;//3)加入S 战队//3)借东风for (int j = h[t];j != -1; j = ne[j]){int i = e[j];dist[i] = min(dist[i],dist[t]+w[j]);//更新dist[j]} }
}int main(){memset (h,-1,sizeof (h));//初始化邻接表cin >> n >>m;while (m--)//读入m条边{int a,b,w;cin >> a >> b >> w;add (a,b,w);}Dijkstra();if (dist[n] != 0x3f3f3f3f)//如果dist[n]被更新了,那么一定存在从1号节点到n号节点的最短距离路径cout << dist[n];elsecout << "-1";
}
关于存储图的适合,没有考虑重边和自环的影响?
因为在第三步更新的时候,即使邻接表那条单链上有两个一样编号的节点,但是第三步更新的时候,还是会让对应编号节点的dist为最小。所以即使有重边也不影响
3.4:数据结构优化
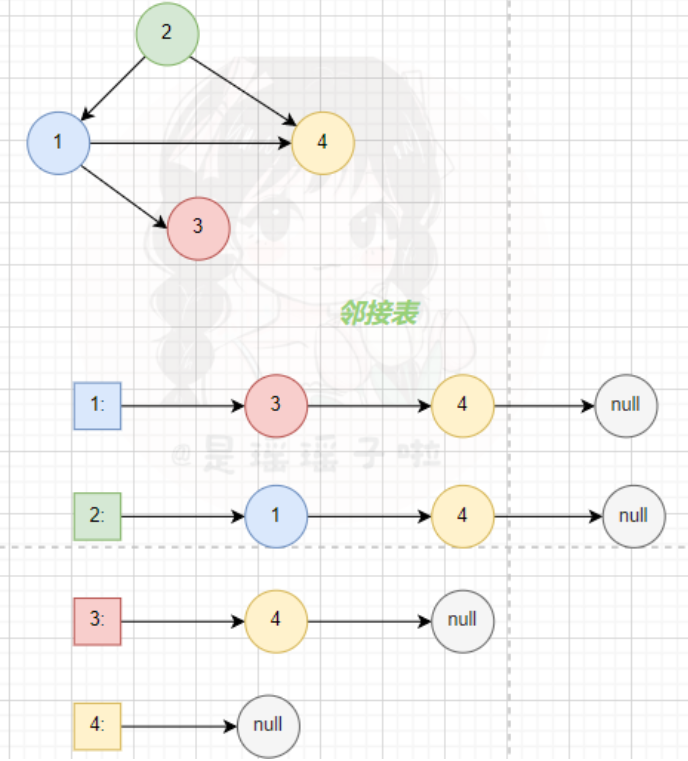
上面我们是采用邻接表来存储图,邻接表的原理如下。邻接表是适合稀疏图,当边比较多,也就是稠密图时,我们采用邻接矩阵来存储图。即g[a][b]的值为编号为a的节点a到编号为b的节点b之间的距离。
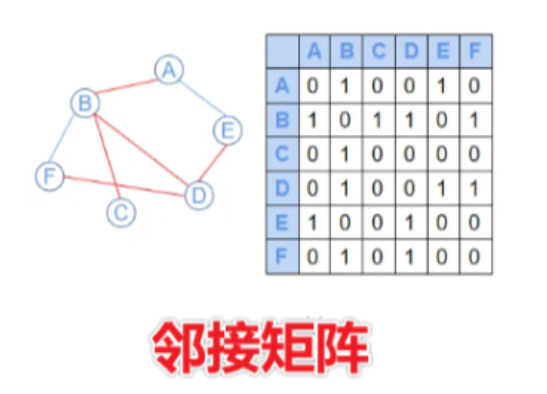
使用邻接矩阵,注意去重边,因为邻接矩阵只允许a→b的距离唯一。
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 510;int n,m;int g[N][N];//邻接矩阵存储图
int dist[N];
bool st[N];int dijkstra(){memset(dist,0x3f,sizeof(dist)); dist[1] = 0;for(int i = 0; i < n; i++){int t = -1;for (int j = 1; j <= n; j ++)if (!st[j] && (t == -1|| dist[t] > dist[j]))t = j;st[t] = true;for (int j = 1; j <= n; j++)dist[j] = min(dist[j],dist[t] + g[t][j]);}if (dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}int main(){scanf("%d%d",&n,&m);memset(g,0x3f,sizeof g);//初始化邻接矩阵while(m--){int a,b,c;scanf("%d%d%d",&a,&b,&c);g[a][b] = min(g[a][b],c);//去除重边}int t = dijkstra();printf("%d\n",t);return 0;
}
3.3:算法分析
算法时间复杂度:时间复杂是 O(n2+m)O(n2+m), n 表示点数,m表示边数
耗时的主要地方在于第2)步,找最小,每次都需要遍历一遍dist数组,完全没有必要。可以使用小根堆来优化(小根堆的数据结构可以自己来实现(推荐),或者用库中的)
四、使用小根堆来优化Dijkstra算法
这个定义的heap,完全可以看作集合V-S的具体化!通过这个小根堆,可以直接取出(取出+删除)V-S集合的最小值。
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>//堆的头文件using namespace std;typedef pair<int, int> PII;//堆里存储距离和节点编号const int N = 1e6 + 10;int n, m;//节点数量和边数
int h[N], w[N], e[N], ne[N], idx;//邻接表存储图
int dist[N];//存储距离
bool st[N];//存储状态void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}int dijkstra()
{memset(dist, 0x3f, sizeof dist);//距离初始化为无穷大dist[1] = 0;priority_queue<PII, vector<PII>, greater<PII>> heap;//小根堆heap.push({0, 1});//插入距离和节点编号while (heap.size()){auto t = heap.top();//取距离源点最近的点heap.pop();int ver = t.second, distance = t.first;//ver:节点编号,distance:源点距离ver 的距离if (st[ver]) continue;//如果距离已经确定,则跳过该点st[ver] = true;for (int i = h[ver]; i != -1; i = ne[i])//更新ver所指向的节点距离{int j = e[i];if (dist[j] > dist[ver] + w[i]){dist[j] = dist[ver] + w[i];heap.push({dist[j], j});//距离变小,则入堆}}}if (dist[n] == 0x3f3f3f3f) return -1;return dist[n];
}int main()
{scanf("%d%d", &n, &m);memset(h, -1, sizeof h);while (m -- ){int a, b, c;scanf("%d%d%d", &a, &b, &c);add(a, b, c);}cout << dijkstra() << endl;return 0;
}使用小根堆后,找到 t 的耗时从 O(n^2) 将为了 O(1)。每次更新 dist 后,需要向堆中插入更新的信息。所以更新dist的时间复杂度有 O(e) 变为了 O(elogn)。总时间复杂度有 O(n^2) 变为了 O(n + elongn)。适用于稀疏图。
五、深入和反思
最开始我们说到,Dijkstra算法只适用于边的权重都是正数的情况。为什么负权边不行呢?
看一个Dijkstra算法失效的例子:
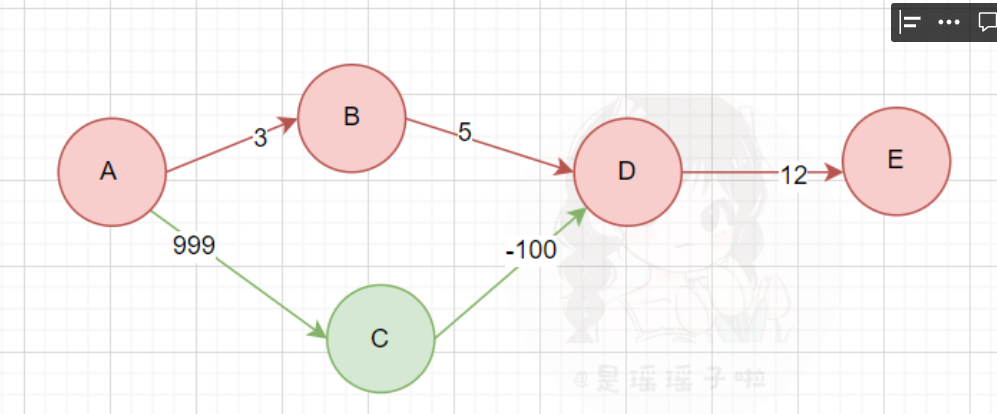
A→B→D→E,确定dist[E]=20,dist[D]=8
然后A→C→D虽然更新了D点的dist,使之正确dist[D]=-1,但是由于D已经被遍历过,无法通过D来更新E,导致最终求出的A→E的最小距离出错。
为什么呢?
D的dist的正确性不受负权的影响,是因为负权指向的是D,在更新节点,更新dist的时候,会更新掉D的错误值。但E就不一样了,在当前局部,只有D一个经过它,D一旦遍历过后,更新了E。当经过C到D时,无法再通过正确的D去更新E!
如果全部是正值的话,在A→D时,能一下子确定当前真正的dist[D]!再dist[D]+12,那dist[E]也是正确的!
所以根本原因在于,存在负权边,dist[D]的真值不能在更新dist[E]之前确定。
最后是我个人总结的理解:
💐在Dijkstra算法视角,把B遍历并进行相关更新后,它当前得知了如下情况:dist[A] = 0,dist[B] = 2,dist[D] = 5,dist[C] = 999,dist[D] = 999+C,C>0,Dijkstra当然会放弃A-C-D这条路,可是C其实<0,这条路不该被放弃,反而A-C-D的路径长度很有可能会小于A-B-C的长度,正是由于Dijkstra的这点输入,导致出现负权边时,结果不正确,再说,人家的正确性本来就是建立在所有边的权重都>0的基础上!

- Java岛冒险记【从小白到大佬之路】
- LeetCode每日一题–进击大厂
- 算法
相关文章:

【算法基础】一篇文章彻底弄懂Dijkstra算法|多图解+代码详解
博主简介:努力学习的大一在校计算机专业学生,热爱学习和创作。目前在学习和分享:算法、数据结构、Java等相关知识。博主主页: 是瑶瑶子啦所属专栏: 算法 ;该专栏专注于蓝桥杯和ACM等算法竞赛🔥近期目标&…...

第二十三天01MySQL多表查询与事务
目录 1. 多表查询 1.1 概述 1.1.1 数据准备 1.1.2 介绍 1.1.3 分类 1.2 内连接 1.2.1 语法 1.2.2 案例演示 1.3 外连接 1.3.1 语法 1.3.2 案例演示 1.4 子查询 1.4.1 介绍 1.4.2 标量子查询 1.4.3 列子查询 1.4.4 行子查询 1.4.5 表子查询 1.5 案例 1.5.1 介…...
TCP协议详解
1.TCP的准备条件在古代的时候,古人们经常写书信进行交流,写书信的前提是你要知道这份信是要寄给谁在网络中,我们通过ip端口号找对目标对象,但是现在网站一般会对ip端口注册一个域名,所以我们一般就是对域名进行查找&am…...
Activiti7与Spring、Spring Boot整合开发
Activiti整合Spring 一、Activiti与Spring整合开发 1.1 Activiti与Spring整合的配置 1)、在pom.xml文件引入坐标 如下 <properties><slf4j.version>1.6.6</slf4j.version><log4j.version>1.2.12</log4j.version> </properties> <d…...
基于SpringBoot实现冬奥会运动会科普平台【源码+论文】
基于SpringBoot实现冬奥会科普平台演示开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包&#…...

一文吃透SpringBoot整合mybatis-plus(保姆式教程)
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
编程练习答案 第4章 复合类型)
C++ primer plus(第六版)编程练习答案 第4章 复合类型
一、程序清单 arrayone.cpp // arrayone.cpp -- small arrays of integers #include <iostream> int main() {using namespace std;int yams[3]; // creates array with three elementsyams[0] = 7; // assign value to first elementyams[1] = 8;yams[2] = 6;i…...
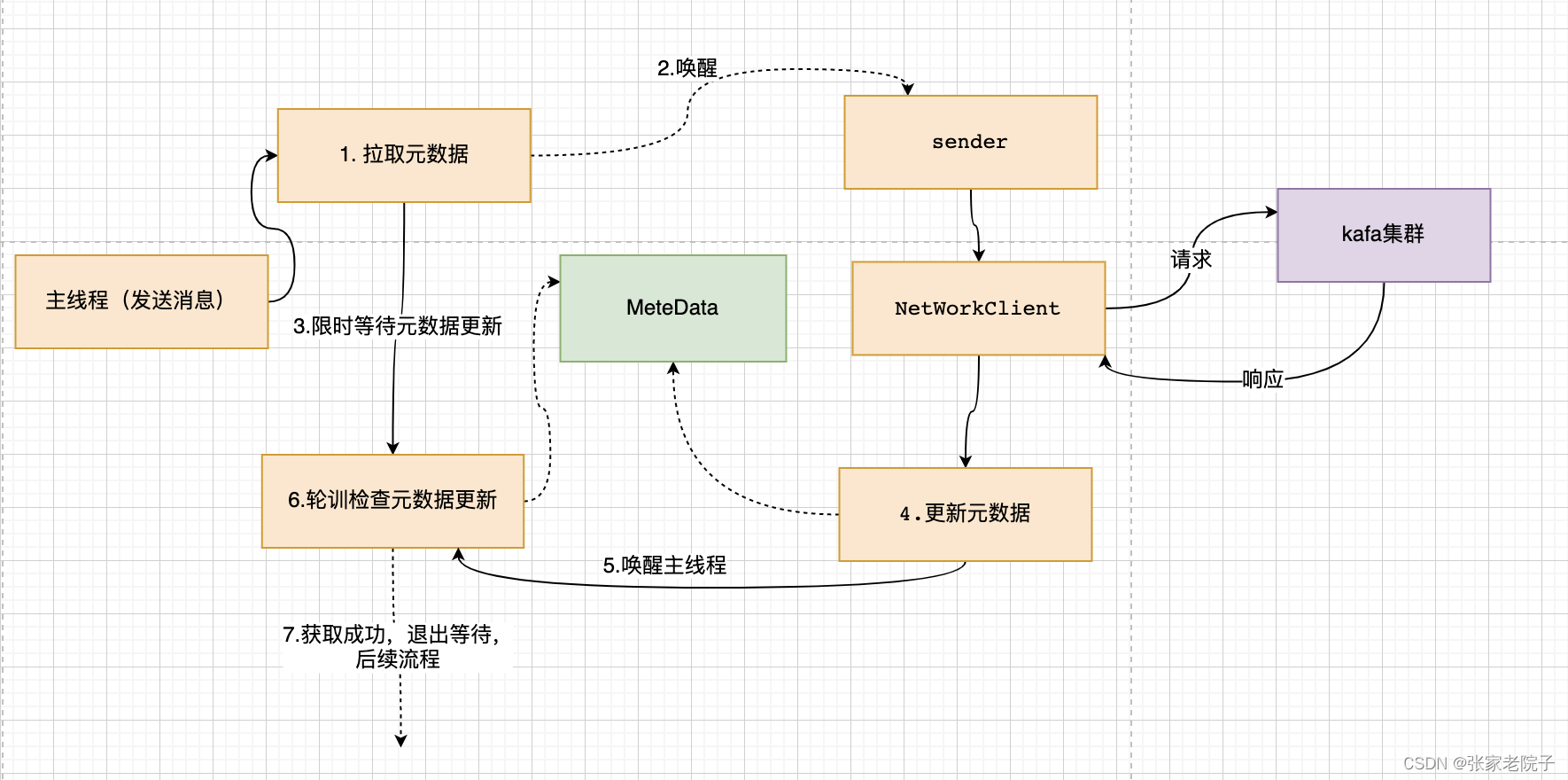
Kafka源码分析之Producer(一)
总览 根据kafka的3.1.0的源码example模块进行分析,如下图所示,一般实例代码就是我们分析源码的入口。 可以将produce的发送主要流程概述如下: 拦截器对发送的消息拦截处理; 获取元数据信息; 序列化处理;…...

springboot校友社交系统
050-springboot校友社交系统演示录像开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7(一定要5.7版本) 数据库工具:Navicat11 开发软件:e…...

python flask项目部署
flask上传服务器pyhon安装下载Anacondasudo wget https://mirrors.tuna.tsinghua.edu.cn/anaconda/archive/Anaconda3-5.3.1-Linux-x86_64.sh可根据需要安装对应的版本https://repo.anaconda.com/archive/解压anaconda压缩包bash Anaconda3-5.3.1-Linux-x86_64.sh解压过程中会…...
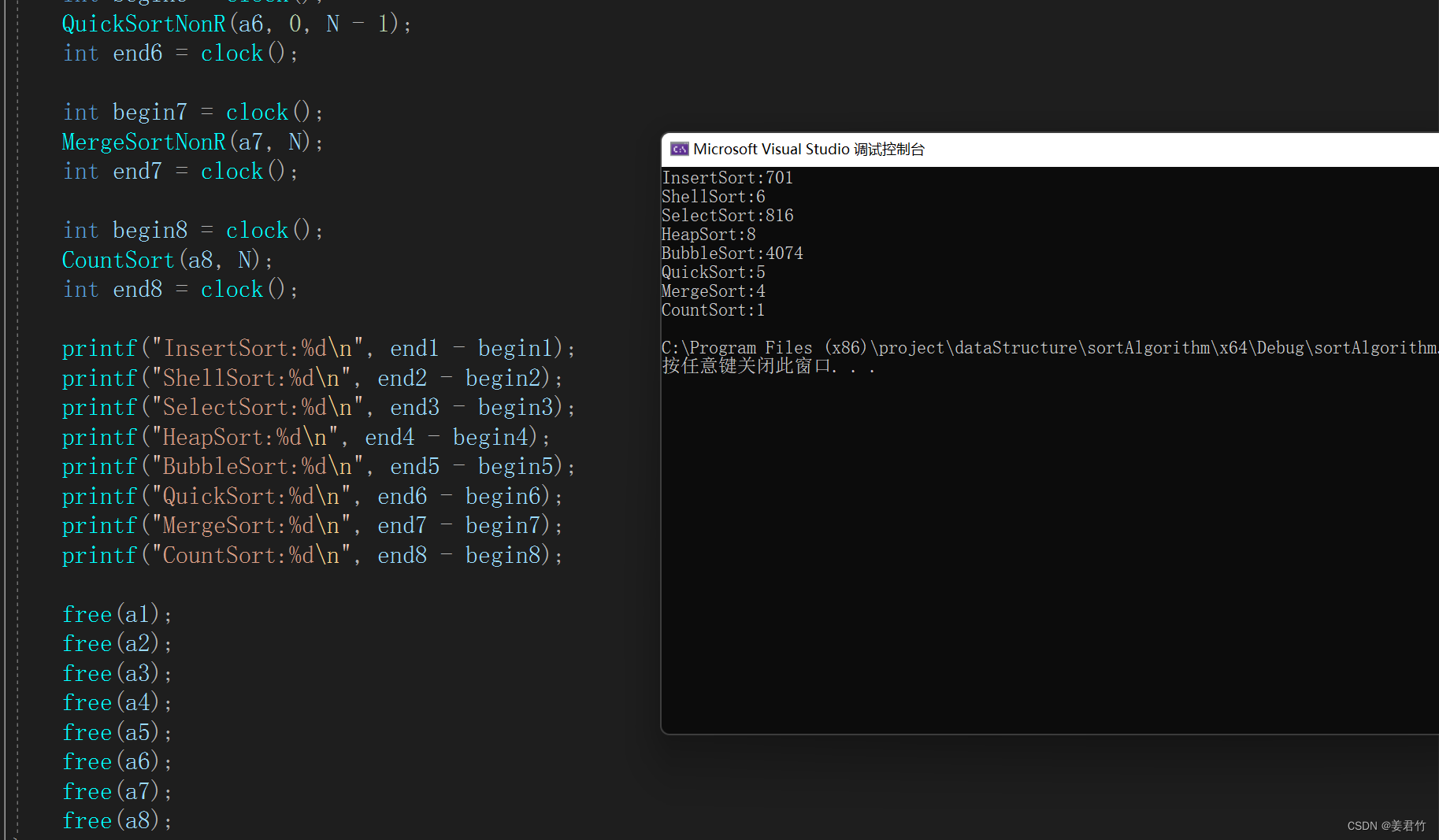
常见排序算法(C语言实现)
文章目录排序介绍插入排序直接插入排序希尔排序选择排序选择排序堆排序交换排序冒泡排序快速排序递归实现Hoare版本挖坑法前后指针版本非递归实现Hoare版本挖坑法前后指针版本快排的优化三值取中小区间优化归并排序递归实现非递归实现计数排序排序算法复杂度及稳定性分析不同算…...

基于jsp+ssm+springboot的小区物业管理系统【设计+论文+源码】
摘 要随着科学技术的飞速发展,各行各业都在努力与现代先进技术接轨,通过科技手段提高自身的优势;对于小区物业管理系统当然也不能排除在外,随着网络技术的不断成熟,带动了小区物业管理系统,它彻底改变了过去…...

Elasticsearch 学习+SpringBoot实战教程(三)
需要学习基础的可参照这两文章 Elasticsearch 学习SpringBoot实战教程(一) Elasticsearch 学习SpringBoot实战教程(一)_桂亭亭的博客-CSDN博客 Elasticsearch 学习SpringBoot实战教程(二) Elasticsearch …...

try-with-resource
try-with-resource是Java 7中引入的新特性,它可以方便地管理资源,自动关闭资源,从而避免了资源泄漏的问题。 作用 使用try-with-resource语句可以简化代码,避免了手动关闭资源的繁琐操作,同时还可以保证资源的正确关闭…...

leetcode148_排序链表的3种解法
1. 题目2. 解答 2.1. 解法12.2. 解法22.3. 解法3 1. 题目 给你链表的头结点head,请将其按升序排列并返回排序后的链表。 /*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullp…...
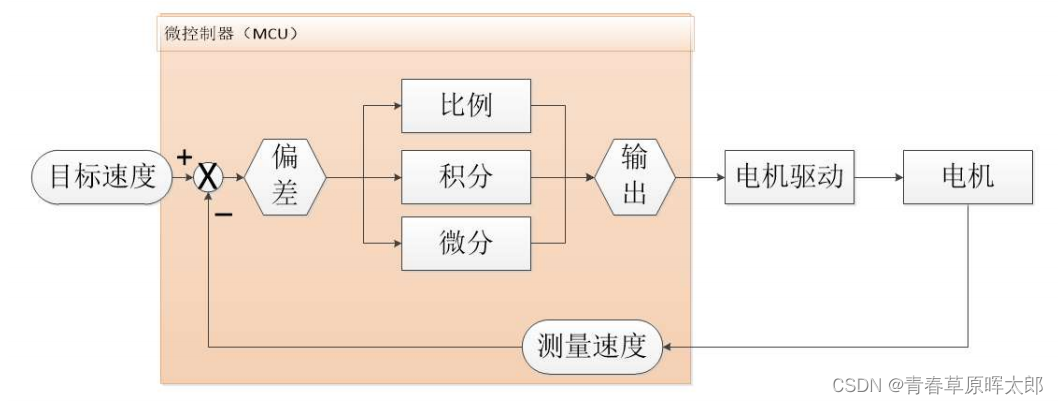
使用stm32实现电机的PID控制
使用stm32实现电机的PID控制 PID控制应该算是非常古老而且应用非常广泛的控制算法了,小到热水壶温度控制,大到控制无人机的飞行姿态和飞行速度等等。在电机控制中,PID算法用的尤为常见。 文章目录使用stm32实现电机的PID控制一、位置式PID1.计…...

数学原理—嵌入矩阵
目录 1.嵌入矩阵的基本作用 2.嵌入矩阵的数学解释 3.嵌入矩阵在联合分布适应中的数学推导主要包括以下几个步骤 4.在JDA中,怎么得到嵌入矩阵 5.联合分布自适应中如何得到嵌入矩阵 (另一种解释) 1.嵌入矩阵的基本作用 在机器学习中&a…...

English Learning - L2 语音作业打卡 辅音翘舌音 [ʃ] [ʒ] 空气摩擦音 [h] Day31 2023.3.23 周四
English Learning - L2 语音作业打卡 辅音翘舌音 [ʃ] [ʒ] 空气摩擦音 [h] Day31 2023.3.23 周四💌发音小贴士:💌当日目标音发音规则/技巧:翘舌音 [ʃ] [ʒ]空气摩擦音 [h]🍭 Part 1【热身练习】🍭 Part2【练习内容】…...
记录springboot+vue+fastdfs实现简易的文件(上传、下载、删除、预览)操作
前言说明:springboot vue FastDFS实现文件上传(支持预览)升级版 FASTDFS部分 FASTDFS安装过程:基于centos 7安装FastDFS文件服务器 SpringBoot部分 springboot源码实现 package com.core.doc.controller;import com.baomid…...
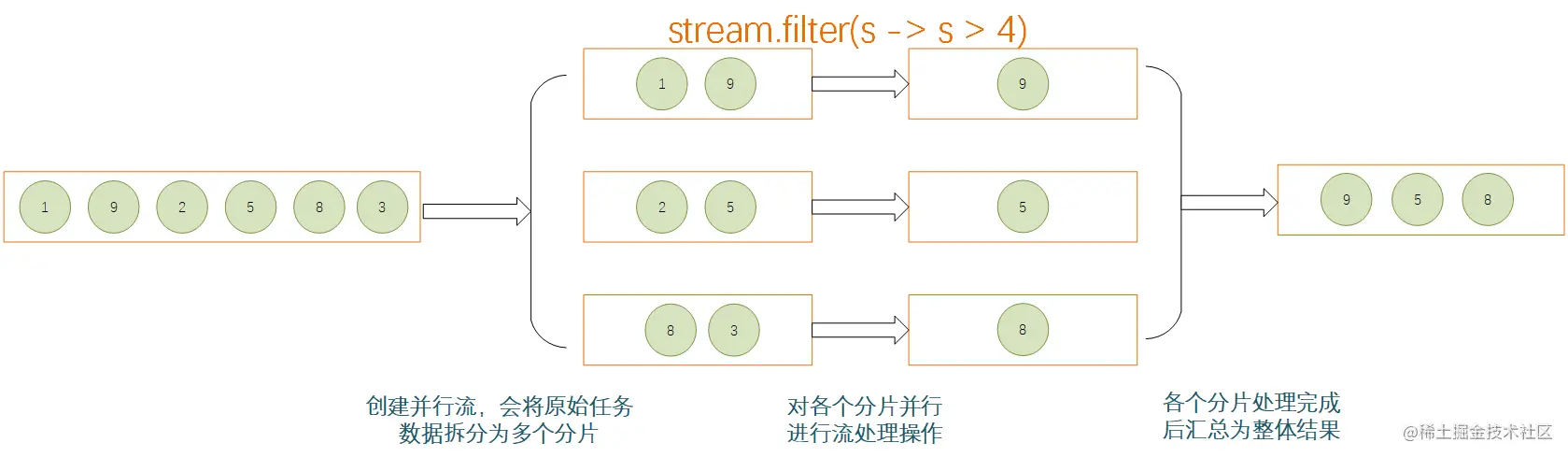
Java中循环使用Stream应用场景
在JAVA中,涉及到对数组、Collection等集合类中的元素进行操作的时候,通常会通过循环的方式进行逐个处理,或者使用Stream的方式进行处理。例如,现在有这么一个需求:从给定句子中返回单词长度大于5的单词列表,…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...

raid存储技术
1. 存储技术概念 数据存储架构是对数据存储方式、存储设备及相关组件的组织和规划,涵盖存储系统的布局、数据存储策略等,它明确数据如何存储、管理与访问,为数据的安全、高效使用提供支撑。 由计算机中一组存储设备、控制部件和管理信息调度的…...
