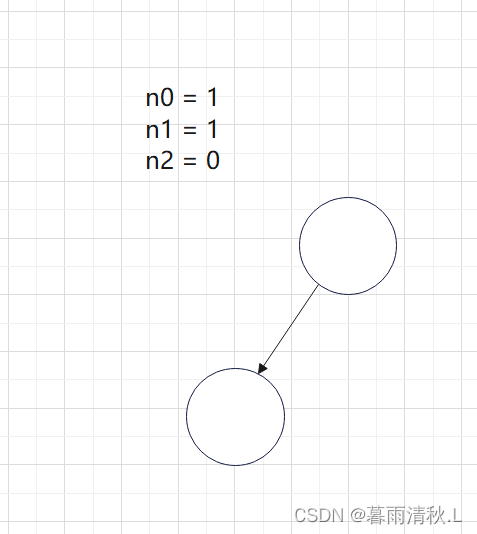走进二叉树的世界 ———性质讲解
二叉树的性质和证明
- 前言
- 1.二叉树的概念和结构
- 特殊的二叉树:
- 二叉树的性质
前言
本篇博客主要讲述的是有关二叉树的一些概念,性质以及部分性质的相关证明,如果大伙发现了啥错误,可以在评论区指出😘😘
1.二叉树的概念和结构
一棵二叉树是节点的一个有限集合,该集合:
- 或者为空
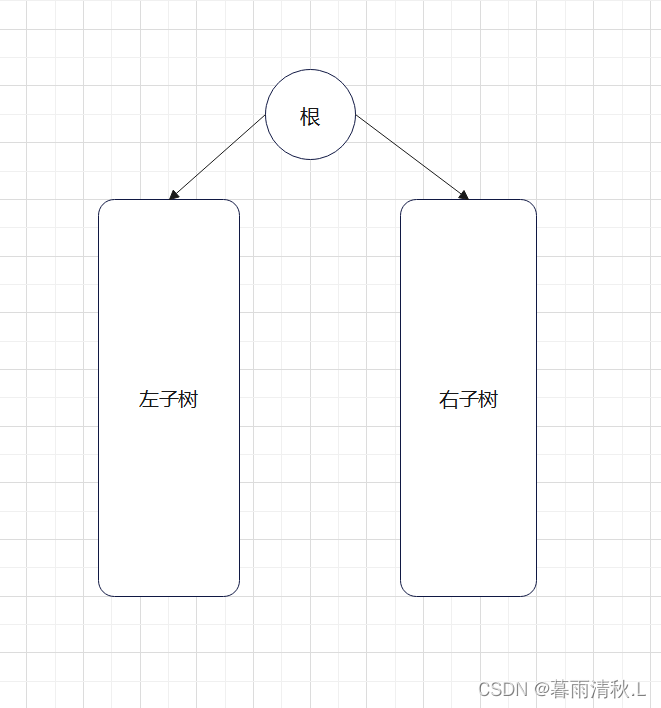
2.由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
如下图所示:
特殊的二叉树:
- 满二叉树:一个二叉树,每一层的节点都达到最大值,这个二叉树就是满二叉树。也就是说,如果一个二叉树的层次为k,且结点总数是2^k-1,这棵树就是满二叉树。
由于每层都是满的,所以节点总数:
2^0 + 2^0 + 2^1 + ······+ 2^(k-1) = 2^k - 1
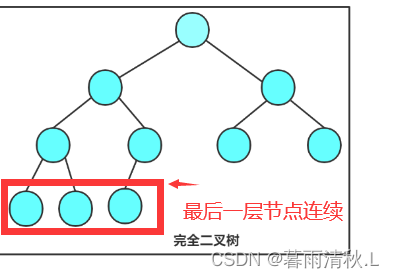
- **完全二叉树:**完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为k的,有n个节点的二叉树,当且仅当其每个节点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。(通俗的来讲,就是当二叉树的前k-1层为满二叉树,最后一层的节点连续排布时就是完全二叉树)
从该定义同时也可以知道,满二叉树是一个特殊的完全二叉树。
如下图所示即是满二叉树:
二叉树的性质
- 若规定根节点的层数是1,则一颗非空二叉树第i层上最多有2^(i-1)个结点。(根据二叉树的结构不难看出)
- 若规定根结点的层数为1,则深度为h的二叉树的最大结点数是2h−12^h-12h−1.
上面在讲解满二叉树时已经给出证明。
- 对于任何一棵二叉树,如果度为0其叶节点个数为n0n_0n0,度为2的分支结点个数为n2n_2n2,则有n0n_0n0 = n2n_2n2 + 。
这里提供两种方法进行帮助理解:
1.关系推导:
(1)首先,对一个只有根节点的树添加一个结点,此时度为0的结点数不点,也就是增加一个度为1的结点,并不影响度为0的结点和度为2的结点个数。
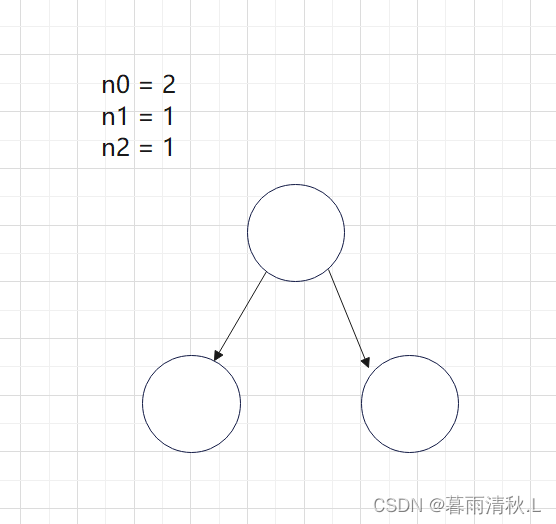
(2)在此之后,每次多一个度为2的结点数,度为0的结点数也会增加一个,所以度为0的结点数总是比度为2的结点数多1。
2. 数学推导
已知一棵二叉树的结点总数为
SSS = n0n_0n0+n1n_1n1+n2n_2n2
SSS = n2∗2n_2*2n2∗2 + n1∗1n_1*1n1∗1 + n0∗0n_0*0n0∗0
联立两式即可得出n0n_0n0 = n2+1n_2+1n2+1
- 若规定根结点的层数为1,具有n个结点的满二叉树的深度,h=log2(n+1)log_2(n+1)log2(n+1)。
该性质的证明即是结点总个数的逆推导。
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有结点从0开始编号,则对于序号为i的结点有:
- 若i>0,i位置结点的双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
- 若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
相关文章:
走进二叉树的世界 ———性质讲解
二叉树的性质和证明前言1.二叉树的概念和结构特殊的二叉树:二叉树的性质前言 本篇博客主要讲述的是有关二叉树的一些概念,性质以及部分性质的相关证明,如果大伙发现了啥错误,可以在评论区指出😘😘 1.二叉树…...

【SSM】Spring + SpringMVC +MyBatis 框架整合
个人简介:Java领域新星创作者;阿里云技术博主、星级博主、专家博主;正在Java学习的路上摸爬滚打,记录学习的过程~ 个人主页:.29.的博客 学习社区:进去逛一逛~ SSM框架整合一、导入相关依赖二、配置web.xml文…...

【算法基础】一篇文章彻底弄懂Dijkstra算法|多图解+代码详解
博主简介:努力学习的大一在校计算机专业学生,热爱学习和创作。目前在学习和分享:算法、数据结构、Java等相关知识。博主主页: 是瑶瑶子啦所属专栏: 算法 ;该专栏专注于蓝桥杯和ACM等算法竞赛🔥近期目标&…...

第二十三天01MySQL多表查询与事务
目录 1. 多表查询 1.1 概述 1.1.1 数据准备 1.1.2 介绍 1.1.3 分类 1.2 内连接 1.2.1 语法 1.2.2 案例演示 1.3 外连接 1.3.1 语法 1.3.2 案例演示 1.4 子查询 1.4.1 介绍 1.4.2 标量子查询 1.4.3 列子查询 1.4.4 行子查询 1.4.5 表子查询 1.5 案例 1.5.1 介…...
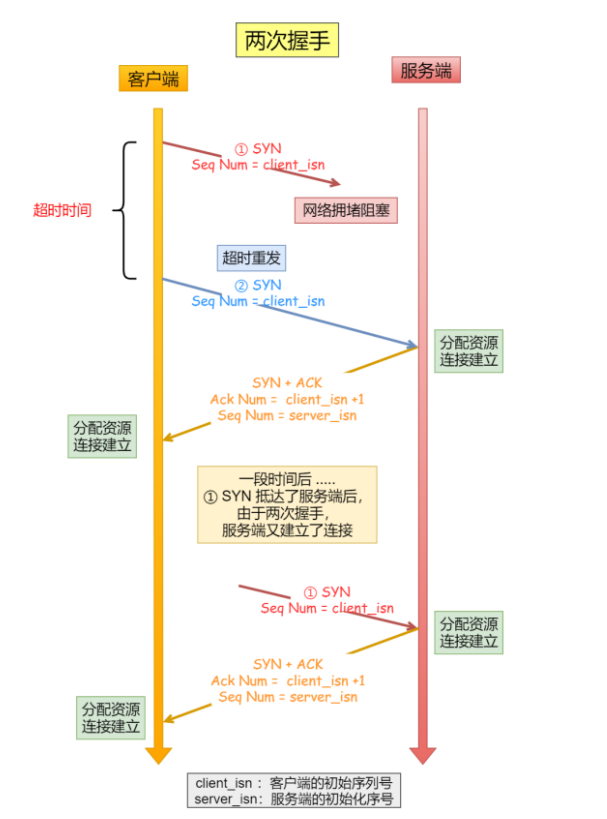
TCP协议详解
1.TCP的准备条件在古代的时候,古人们经常写书信进行交流,写书信的前提是你要知道这份信是要寄给谁在网络中,我们通过ip端口号找对目标对象,但是现在网站一般会对ip端口注册一个域名,所以我们一般就是对域名进行查找&am…...
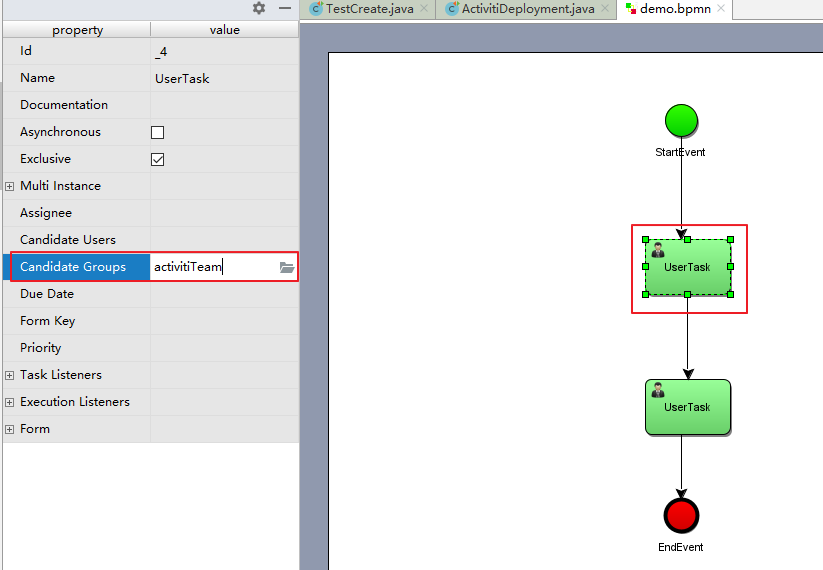
Activiti7与Spring、Spring Boot整合开发
Activiti整合Spring 一、Activiti与Spring整合开发 1.1 Activiti与Spring整合的配置 1)、在pom.xml文件引入坐标 如下 <properties><slf4j.version>1.6.6</slf4j.version><log4j.version>1.2.12</log4j.version> </properties> <d…...
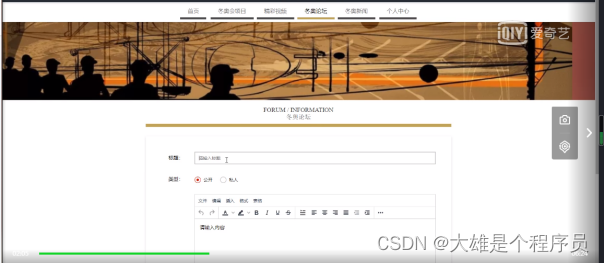
基于SpringBoot实现冬奥会运动会科普平台【源码+论文】
基于SpringBoot实现冬奥会科普平台演示开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包&#…...

一文吃透SpringBoot整合mybatis-plus(保姆式教程)
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...
编程练习答案 第4章 复合类型)
C++ primer plus(第六版)编程练习答案 第4章 复合类型
一、程序清单 arrayone.cpp // arrayone.cpp -- small arrays of integers #include <iostream> int main() {using namespace std;int yams[3]; // creates array with three elementsyams[0] = 7; // assign value to first elementyams[1] = 8;yams[2] = 6;i…...
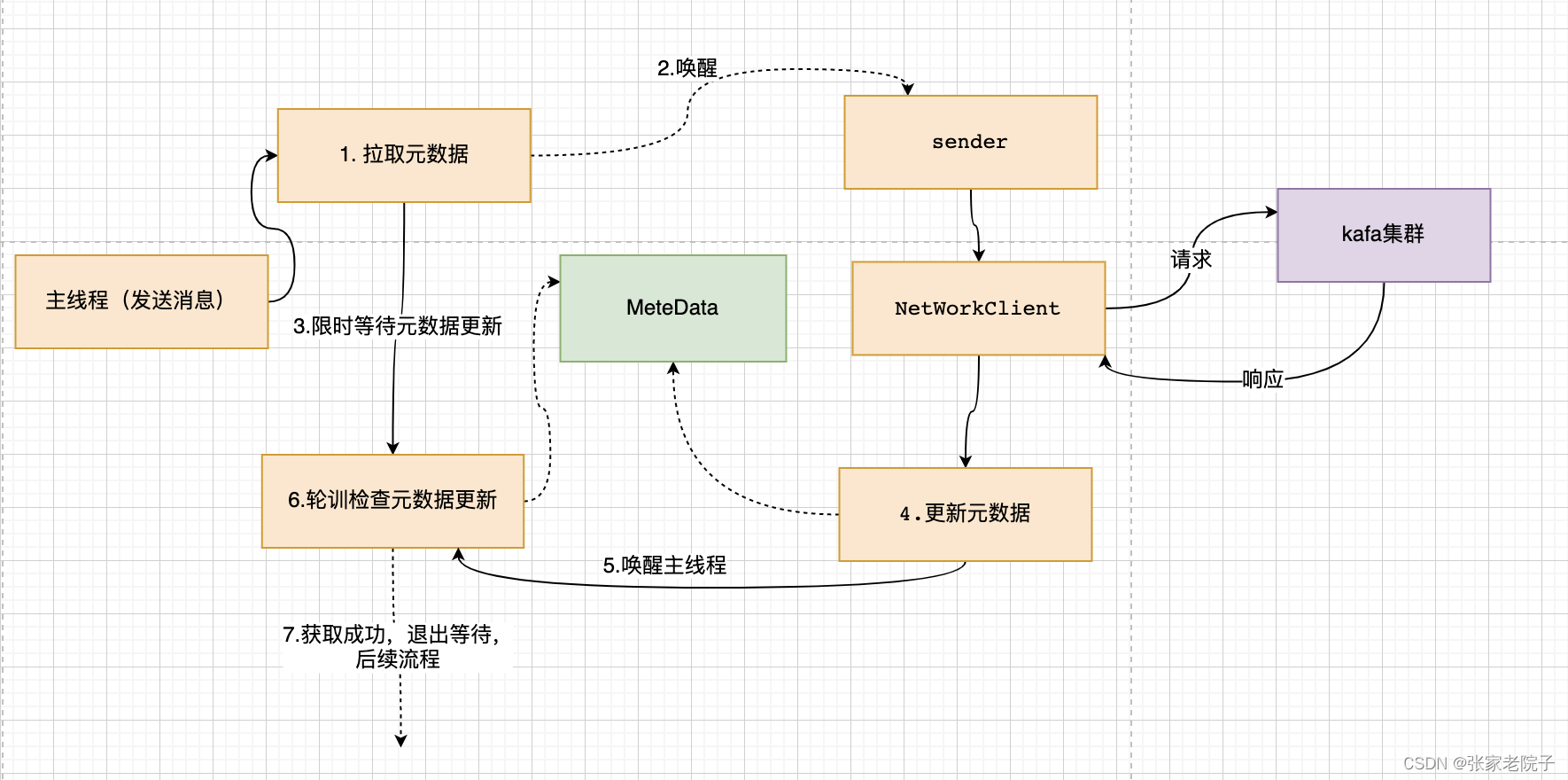
Kafka源码分析之Producer(一)
总览 根据kafka的3.1.0的源码example模块进行分析,如下图所示,一般实例代码就是我们分析源码的入口。 可以将produce的发送主要流程概述如下: 拦截器对发送的消息拦截处理; 获取元数据信息; 序列化处理;…...

springboot校友社交系统
050-springboot校友社交系统演示录像开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7(一定要5.7版本) 数据库工具:Navicat11 开发软件:e…...

python flask项目部署
flask上传服务器pyhon安装下载Anacondasudo wget https://mirrors.tuna.tsinghua.edu.cn/anaconda/archive/Anaconda3-5.3.1-Linux-x86_64.sh可根据需要安装对应的版本https://repo.anaconda.com/archive/解压anaconda压缩包bash Anaconda3-5.3.1-Linux-x86_64.sh解压过程中会…...
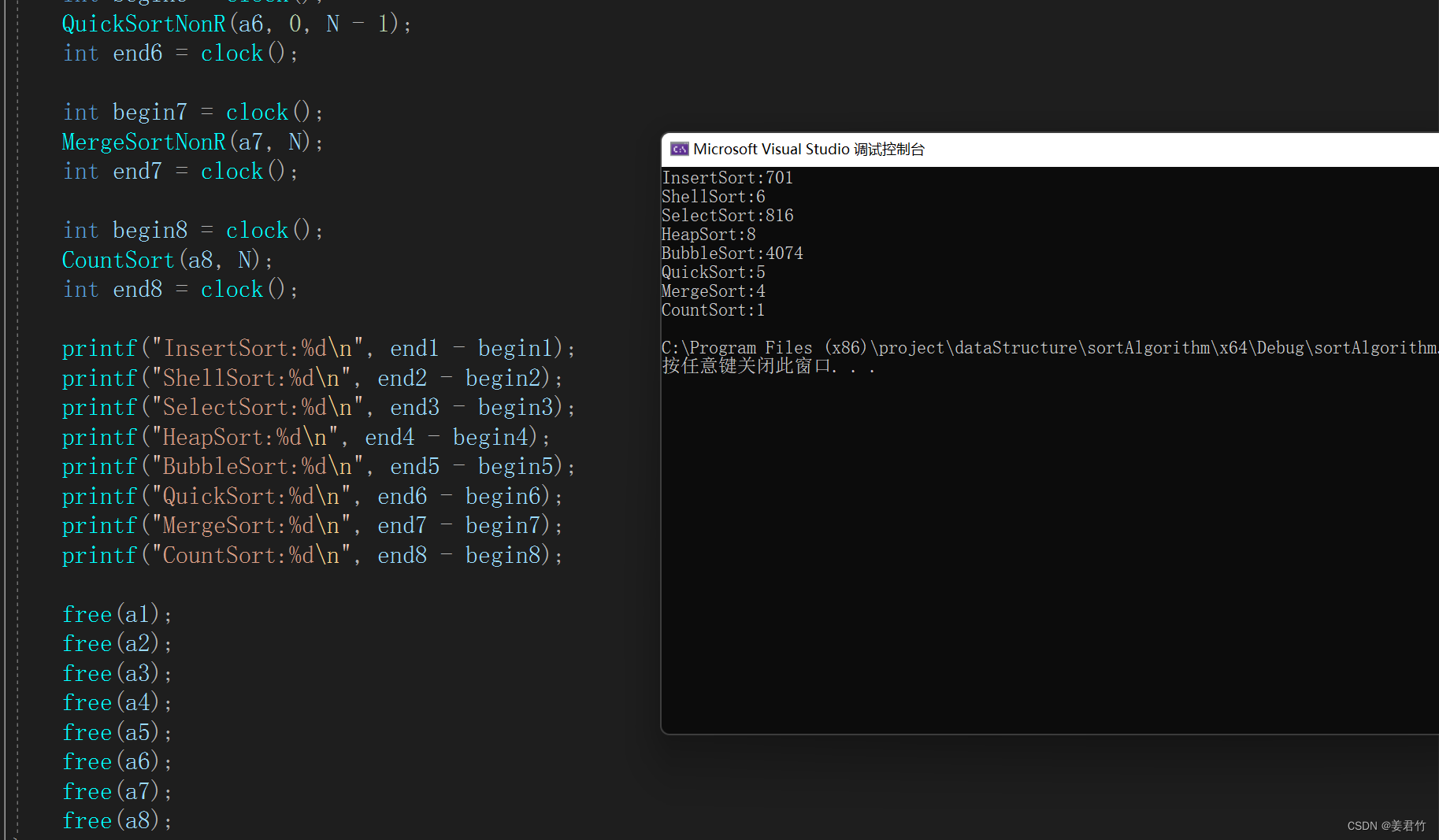
常见排序算法(C语言实现)
文章目录排序介绍插入排序直接插入排序希尔排序选择排序选择排序堆排序交换排序冒泡排序快速排序递归实现Hoare版本挖坑法前后指针版本非递归实现Hoare版本挖坑法前后指针版本快排的优化三值取中小区间优化归并排序递归实现非递归实现计数排序排序算法复杂度及稳定性分析不同算…...

基于jsp+ssm+springboot的小区物业管理系统【设计+论文+源码】
摘 要随着科学技术的飞速发展,各行各业都在努力与现代先进技术接轨,通过科技手段提高自身的优势;对于小区物业管理系统当然也不能排除在外,随着网络技术的不断成熟,带动了小区物业管理系统,它彻底改变了过去…...

Elasticsearch 学习+SpringBoot实战教程(三)
需要学习基础的可参照这两文章 Elasticsearch 学习SpringBoot实战教程(一) Elasticsearch 学习SpringBoot实战教程(一)_桂亭亭的博客-CSDN博客 Elasticsearch 学习SpringBoot实战教程(二) Elasticsearch …...

try-with-resource
try-with-resource是Java 7中引入的新特性,它可以方便地管理资源,自动关闭资源,从而避免了资源泄漏的问题。 作用 使用try-with-resource语句可以简化代码,避免了手动关闭资源的繁琐操作,同时还可以保证资源的正确关闭…...

leetcode148_排序链表的3种解法
1. 题目2. 解答 2.1. 解法12.2. 解法22.3. 解法3 1. 题目 给你链表的头结点head,请将其按升序排列并返回排序后的链表。 /*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullp…...
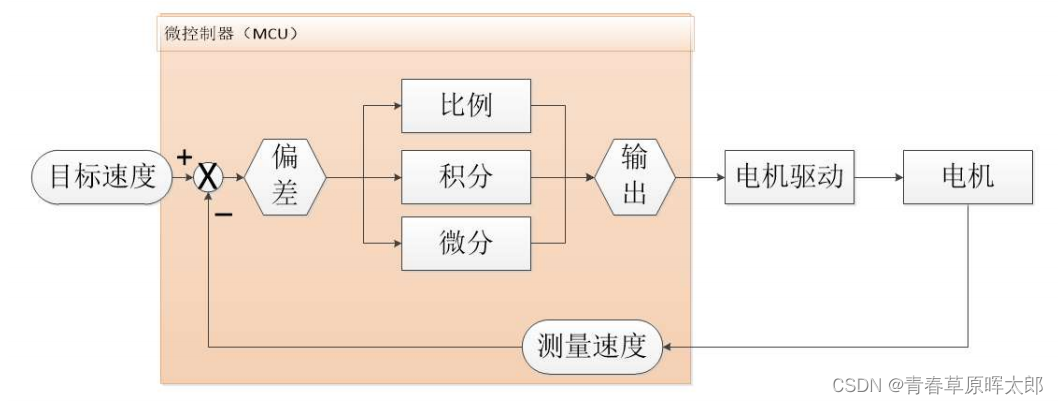
使用stm32实现电机的PID控制
使用stm32实现电机的PID控制 PID控制应该算是非常古老而且应用非常广泛的控制算法了,小到热水壶温度控制,大到控制无人机的飞行姿态和飞行速度等等。在电机控制中,PID算法用的尤为常见。 文章目录使用stm32实现电机的PID控制一、位置式PID1.计…...

数学原理—嵌入矩阵
目录 1.嵌入矩阵的基本作用 2.嵌入矩阵的数学解释 3.嵌入矩阵在联合分布适应中的数学推导主要包括以下几个步骤 4.在JDA中,怎么得到嵌入矩阵 5.联合分布自适应中如何得到嵌入矩阵 (另一种解释) 1.嵌入矩阵的基本作用 在机器学习中&a…...

English Learning - L2 语音作业打卡 辅音翘舌音 [ʃ] [ʒ] 空气摩擦音 [h] Day31 2023.3.23 周四
English Learning - L2 语音作业打卡 辅音翘舌音 [ʃ] [ʒ] 空气摩擦音 [h] Day31 2023.3.23 周四💌发音小贴士:💌当日目标音发音规则/技巧:翘舌音 [ʃ] [ʒ]空气摩擦音 [h]🍭 Part 1【热身练习】🍭 Part2【练习内容】…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...