【刷题笔记】删除并获取最大点数粉刷房子

题目一
题目链接:删除并获取最大点数
思路:
- 预处理

- 状态表示

- 状态转移方程

代码如下:
class Solution {
public:int deleteAndEarn(vector<int>& nums) {int N=10001;int arry[N]={0};for(auto x:nums){arry[x]+=x;}//接下来,就是打家劫舍问题vector<int> f(N);vector<int> g(N);f[0]=arry[0];g[0]=0;for(int i=0;i<N;i++){f[i]=g[i-1]+arry[i];g[i]=max(g[i-1],f[i-1]);}return max(f[10000],g[10000]);English}
};
思考:我们是如何将这道题目和打家劫舍问题联系在一起的
这道题目要求必须删除相邻的数据,和打家劫舍问题中的不能偷相邻的两家的东西非常相似。所以我们就可以将本题转化为打家劫舍问题。但是本题的数据不一定是连续的,所以我们需要预处理一步。转化成连续的。
题目二
题目链接:粉刷房子
思路:



代码如下:
class Solution {
public:int minCost(vector<vector<int>>& costs) {int m=costs.size(); if(m==1) return min(costs[0][1],costs[0][0],costs[0][2]);vector<vector<int>>dp(m+1,vector<int>(3));for(int i=1;i<m+1;i++){dp[i][0]=min(dp[i-1][1],dp[i-1][2])+costs[i-1][0];dp[i][1]=min(dp[i-1][0],dp[i-1][2])+costs[i-1][1];dp[i][2]=min(dp[i-1][0],dp[i-1][1])+costs[i-1][2];}return min(dp[m][0],dp[m][1],dp[m][2]);}
};
相关文章:

【刷题笔记】删除并获取最大点数粉刷房子
欢迎来到 破晓的历程的 博客 ⛺️不负时光,不负己✈️ 题目一 题目链接:删除并获取最大点数 思路: 预处理状态表示 状态转移方程 代码如下: class Solution { public:int deleteAndEarn(vector<int>& nums) {int N1…...

【Linux 从基础到进阶】Elasticsearch 搜索服务安装与调优
Elasticsearch 搜索服务安装与调优 引言 Elasticsearch 是一个分布式的、基于 RESTful API 的搜索和分析引擎,专为快速处理大量数据而设计。它经常被用来进行全文搜索、日志和指标分析等操作。本文将介绍如何在 CentOS 和 Ubuntu 系统上安装 Elasticsearch,并进行必要的调优…...

IMU助力JAXA空间站机器人
近日,日本宇宙航空研究开发机构(JAXA)宣布,在国际空间站(ISS)实验舱“希望号”(Kibo)上部署的一款移动摄像机器人将采用Epson M-G370系列惯性测量单元(IMU)。…...

java开发,记录一些注解和架构
最近接了一个项目,说是项目其实也不算是项目,因为是把这个项目赛到其他项目中的。 熟悉一些这个项目的功能,梳理了一下,在代码开发中主要关心pojo、entity、respository、controller、service。 在这里主要记录前3个的流程与作用…...

【2024高教社杯全国大学生数学建模竞赛】B题 生产过程中的决策问题——解题思路 代码 论文
目录 问题 1:抽样检测方案的设计问题 2:生产过程中的决策问题 3:多工序、多零配件的生产决策问题 4:重新分析次品率题目难度分析1. 统计检测方案设计的复杂性(问题 1)2. 多阶段生产决策的复杂性(…...

JUnit 5和Mockito进行单元测试!
1. JUnit 5 基础 JUnit 5是最新的JUnit版本,它引入了许多新特性,包括更灵活的测试实例生命周期、参数化测试、更丰富的断言和假设等。 1.1 基本注解 Test:标记一个方法为测试方法。 BeforeEach:在每个测试方法之前执行。 AfterEac…...

LeetCode 算法:完全平方数 c++
原题链接🔗:完全平方数难度:中等⭐️⭐️ 题目 给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。 完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的…...

深入CSS 布局——WEB开发系列29
CSS 页面布局技术允许我们拾取网页中的元素,并且控制它们相对正常布局流、周边元素、父容器或者主视口/窗口的位置。 一、正常布局流(Normal Flow) CSS的布局基础是“正常流”,也就是页面元素在没有特别指定布局方式时的默认排列…...

视频的容器格式和编码格式详解
视频的容器格式和编码格式是视频文件的两个核心概念,它们相互关联但具有不同的功能。以下是详细的解释: 1. 容器格式 (Container Format) 容器格式,又称封装格式,指的是视频文件的外壳或容器,它用于封装视频、音频、…...
Elasticsearch Mapping 详解
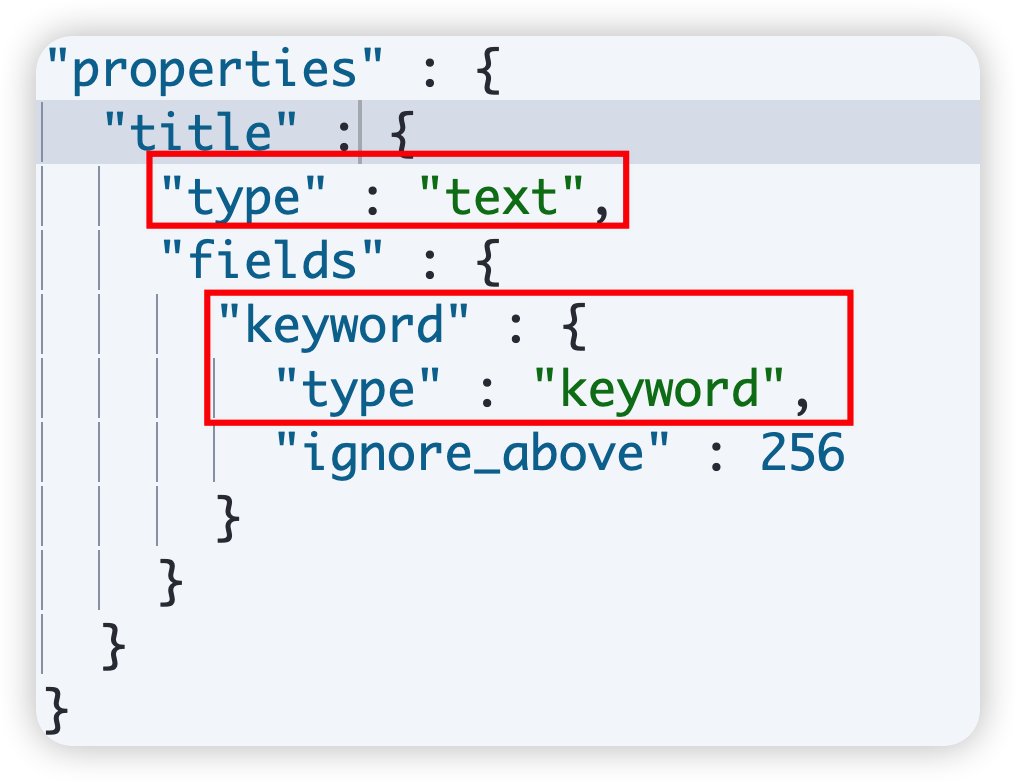
1 概述 映射的基本概念 Mapping 也称之为映射,定义了 ES 的索引结构、字段类型、分词器等属性,是索引必不可少的组成部分。 ES 中的 mapping 有点类似与DB中“表结构”的概念,在 MySQL 中,表结构里包含了字段名称,字…...

WPF 利用视觉树获取指定名称对象、指定类型对象、以及判断是否有验证错误
1.利用视觉树获取指定名称对象 /// <summary> /// Finds a Child of a given item in the visual tree. /// </summary> /// <param name"parent">A direct parent of the queried item.</param> /// <typeparam name"T">T…...
`, `sub()`, `subn()`方法的作用)
了解`re`模块的`split()`, `sub()`, `subn()`方法的作用
在Python中,re模块(即正则表达式模块)提供了强大的字符串处理能力,允许你通过模式匹配来执行复杂的文本搜索、替换和分割等操作。其中,split(), sub(), 和 subn() 方法是re模块中非常实用的几个函数,它们各…...

机器学习交通流量预测实现方案
机器学习交通流量预测实现方案 实现方案 1. 数据预处理 2. 模型选择 3. 模型训练与评估 代码实现 代码解释 小结 🎈边走、边悟🎈迟早会好 交通流量预测是机器学习在智能交通系统中的典型应用,通常用于预测道路上的车辆流量、速度和拥…...

QNN:基于QNN+example重构之后的yolov8det部署
QNN是高通发布的神经网络推理引擎,是SNPE的升级版,其主要功能是: 完成从Pytorch/TensorFlow/Keras/Onnx等神经网络框架到高通计算平台的模型转换; 完成模型的低比特量化(int8),使其能够运行在高…...

Redis实战宝典:开发规范与最佳实践
目录标题 Key命名设计:可读性、可管理性、简介性Value设计:拒绝大key控制Key的生命周期:设定过期时间时间复杂度为O(n)的命令需要注意N的数量禁用命令:KEYS、FLUSHDB、FLUSHALL等不推荐使用事务删除大key设置合理的内存淘汰策略使…...

RPC的实现原理架构
RPC(Remote Procedure Call,远程过程调用)是一种允许程序调用位于不同地址空间或网络上的函数或方法的技术,尽管这些调用看起来像是本地调用。RPC 的实现极大地简化了分布式系统中的通信,避免了开发人员直接处理底层网…...

OpenXR Monado Hello_xr提交Frame
OpenXR Monado Hello_xr提交Frame @src/tests/hello_xr/openxr_program.cpp RenderFrame())xrWaitFrame(m_session, &frameWaitInfo, &frameState)xrBeginFrame(m_session, &frameBeginInfo)std::vector<XrCompositionLayerBaseHeader*> layers;std::vecto…...

huggingface快速下载模型及其配置
大家知道,每次进huggingface里面一个个手动下载文件然后再上传到我们的服务器是很麻烦的。其实huggingface提供了下载整个包的命令,很简单,如下: 1. 进入huggingface官网,随便搜索一个模型,点击右上角的三…...

虚幻5|不同骨骼受到不同伤害|小知识(2)
1.蓝图创建一个结构,B_BoneDamage 结构里添加一个浮点变量,表示伤害倍数 2.当我们创建了一个结构,就需要创建一个数据表格,数据表格可以选择对应的结构 不同骨骼不同倍数伤害,骨骼要对应骨骼网格体的名称 3.把我们br…...

达梦SQL 优化简介
目录 一、定位慢 SQL (一)开启跟踪日志记录 1.跟踪日志记录配置 (二)通过系统视图查看 1.SQL 记录配置 2.查询方式 二、SQL分析方法 (一)执行计划 1.概述 2.查看执行计划 (二&#x…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
