Leetcode3256. 放三个车的价值之和最大 I
Every day a Leetcode
题目来源:3256. 放三个车的价值之和最大 I
解法1:贪心
从大到下排序矩阵所有值, 记为数组v。
转化此题:从r*c个数中选取3个数分别给到车1,车2,和车3,使得符合条件的三数之和最大。

结论:可选前2r+2c+1个最大值作为候选值,在此范围枚举求三数之和最大。
代码:
/** @lc app=leetcode.cn id=3256 lang=cpp** [3256] 放三个车的价值之和最大 I*/// @lc code=start
class Solution
{
public:long long maximumValueSum(vector<vector<int>> &board){int m = board.size(), n = m ? board[0].size() : 0;vector<tuple<int, int, int>> v;for (int i = 0; i < m; i++)for (int j = 0; j < n; j++)v.push_back({board[i][j], i, j});sort(v.begin(), v.end(), greater<tuple<int, int, int>>());long long ans = LONG_LONG_MIN;int range = min(2 * (m + n) + 1, (int)v.size());for (int i = 0; i < range; i++){auto [v1, x1, y1] = v[i];for (int j = i + 1; j < range; j++){auto [v2, x2, y2] = v[j];if (x2 == x1 || y2 == y1)continue;for (int k = j + 1; k < range; k++){auto [v3, x3, y3] = v[k];if (x3 == x1 || y3 == y1 || x3 == x2 || y3 == y2)continue;ans = max(ans, (long long)v1 + v2 + v3);}}}return ans;}
};
// @lc code=end
结果:

复杂度分析:
时间复杂度:O((m+n)3),其中 m 和 n 分别是数组 board 的行数和列数。
空间复杂度:O(m * n),其中 m 和 n 分别是数组 board 的行数和列数。
相关文章:

Leetcode3256. 放三个车的价值之和最大 I
Every day a Leetcode 题目来源:3256. 放三个车的价值之和最大 I 解法1:贪心 从大到下排序矩阵所有值, 记为数组v。 转化此题:从r*c个数中选取3个数分别给到车1,车2,和车3,使得符合条件的三数之和最大。…...

Redis中String类型的基本命令
文章目录 一、String字符串简介二、常见命令setgetmgetmsetsetnxincrincrbydecrdecrbyincrbyfloatappendgetrangesetrangestrlen 三、命令小结四、字符串内部编码五、String典型使用场景1. 缓存(Cache)功能2. 计数功能3. 共享会话(Session)4. 手机验证码…...
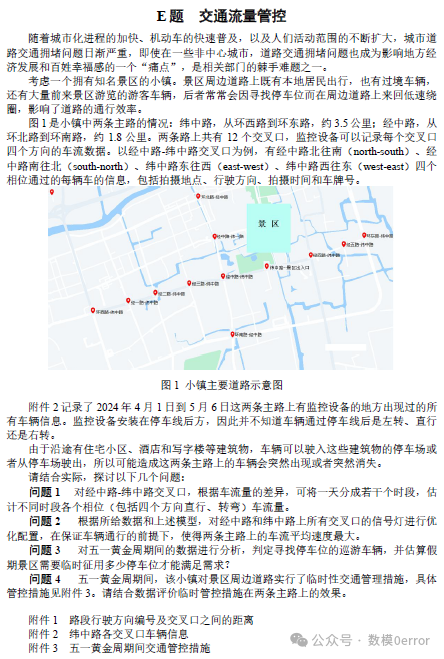
2024 年高教社杯全国大学生数学建模竞赛题目【A/B/C/D/E题】完整思路
↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑ A题是数模类赛事很常见的物理类赛题,需要学习不少相关知识。此题涉及对一个动态系统的建模,模拟…...
HR招聘新员工,如何考察企业文化适配度
要解决文化适配性问题,那在招聘过程中一定要明确企业核心价值观。比如通过制定明确文化价值观手册的方式,向求职者展示企业的使命愿景和价值观。 目前最为理想的考察方式就是线上的人才测评,比如:采用职业价值观测评法࿰…...

AI算力「搅局」座舱SoC
对于芯片巨头来说,汽车是难以割舍的赛道。 这不仅仅是因为「车规级」向来是准入门槛最高的细分市场之一,更重要的原因来自于从PC、智能手机到智能汽车时代,芯片公司都在寻求成为新周期的标杆。 比如,从PC时代的「英特尔」到智能手…...

lvs DR模式调试
DS配置: # cat /etc/keepalived_docker/keepalived.conf ! Configuration File for keepalived global_defs {router_id LVS_70 # 设置lvs的id,在一个网络内应该是唯一的 }vrrp_instance VI_70 {state MASTER # 两个 DS࿰…...

Java线程池的优化策略与最佳实践
哈喽,各位小伙伴们,你们好呀,我是喵手。运营社区:C站/掘金/腾讯云/阿里云/华为云/51CTO;欢迎大家常来逛逛 今天我要给大家分享一些自己日常学习到的一些知识点,并以文字的形式跟大家一起交流,互…...

android面试:解释一下 AsyncTask是什么?
AsyncTask 是 Android 中用于处理异步操作的一个类,它允许在后台线程中执行任务,并在完成后将结果传递回主线程。AsyncTask 主要用于执行短时间的后台操作,例如网络请求、文件读写等,而不阻塞用户界面。 AsyncTask 的主要特点&am…...
(登录功能实现))
Django+Vue3前后端分离学习(四)(登录功能实现)
1、序列化数据: 创建serializers.py的python文件 从rest_framework里导入serializers类: from rest_framework import serializers class LoginSerializer(serializers.Serializer):email serializers.EmailField(requiredTrue, error_messages{&qu…...

机器学习面试:SVM为什么使用对偶函数求解?
支持向量机(SVM)在求解过程中使用对偶函数的原因主要与优化问题的性质、计算效率以及模型的泛化能力有关。以下是对偶函数在 SVM 中使用的详细解释: 1. 原始问题与对偶问题 在 SVM 中,我们的目标是找到一个超平面来最大化分类间…...

RabbitMQ 入门教程
介绍 RabbitMQ 是一个消息中间件,它实现了 AMQP (Advanced Message Queuing Protocol) 协议。本教程将引导你通过几个简单的步骤来学习如何使用 RabbitMQ 发送和接收消息。 环境准备 1. 安装 RabbitMQ - 在你的系统上安装 RabbitMQ: https://www.rabbitmq.com/d…...

docker进阶 compose等
Docker Compose 简介: 比如有100个微服务,不需要手动启动每一个,可以使用docker compose定义运行多个容器,高效管理化。 定义、运行多个容器 YAML file配置文件 single command 命令 写docker-compose.yaml docker-compose …...

[详细建模已更新]2024数学建模国赛高教社杯A题:“板凳龙” 闹元宵 思路代码文章助攻手把手保姆级
A 题 “板凳龙” 闹元宵 “板凳龙”,又称“盘龙”,是浙闽地区的传统地方民俗文化活动。人们将少则几十条,多则上百条的板凳首尾相连,形成蜿蜒曲折的板凳龙。盘龙时,龙头在前领头,龙身和龙尾相随盘旋&#x…...

网络编程(TCP+网络模型)
【1】TCP 初版服务器 #include <stdio.h> #include <sys/types.h> /* See NOTES */ #include <sys/socket.h> #include <netinet/in.h> #include <netinet/ip.h> #include <unistd.h> #include <arpa/inet.h> #include <string.h…...

Docker Image 命令
文章目录 目录 文章目录 1 . Docker镜像是什么? 2 . 镜像命令详解 docker images docker tag docker pull docker rmi docker save 总结 1 . Docker镜像是什么? Docker image 本质上是一个 read-only 只读文件, 这个文件包含了文件系统、 源码、库文件…...

如何在IntelliJ IDEA中将Tab设置为4个空格
前言 IntelliJ IDEA是一个强大的开发工具,支持多种编程语言。为了保持代码整洁一致,开发者经常需要调整编辑器中的Tab和缩进设置。 步骤1: 打开设置 首先,启动IntelliJ IDEA。在主界面上方的菜单栏中找到 File(文件)…...

ASP.NET Core 入门教学十五 异步编程
在ASP.NET Core中,异步编程是一种非常重要的技术,它可以提高应用程序的性能和响应能力。本教程将介绍如何在ASP.NET Core中使用异步编程。 1. 异步编程基础 异步编程允许程序在等待某些操作(如I/O操作)完成时继续执行其他任务&a…...

pycharm 2024.1下载、安装
下载 下载官网: Other Versions - PyCharm 选择需要的版本下载,这里以 2024.1 的版本为例 安装 双击下载好的安装程序,点击下一步 选择安装路径,最好是英文路径;然后下一步 点击完成 激活 网址: Some…...

实变函数精解【18】
文章目录 有限测度有限测度概率测度有限测度与概率测度的关系 σ \sigma σ-有限测度计数测度完备概率测度 参考文献 有限测度 首先,我们来明确“测度”的概念。在数学中,测度是一个将集合映射到非负实数(通常是实数的扩展,包括正…...

【深入解析】AI工作流中的HTTP组件:客户端与服务端执行的区别
在当今快速发展的技术环境中,AI工作流的设计和实现变得愈发重要。尤其是在处理HTTP组件时,前端执行与后端执行之间的区别,往往会对系统的安全性和数据的准确性产生深远的影响。今天,我们就来深入探讨这一话题,揭示前端…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
