数据结构——树和二叉树
目录
一、树的概念
二、树结点之间的关系
三、二叉树
1、满二叉树
2、完全二叉树
四、二叉树的存储
1、顺序存储
2、链式存储
一、树的概念
如果数据和数据之间满足一对多的关系,将其逻辑结构称之为树
如下图:树的根与树的分支存在一对多的关系

将上图具体化,从根节点开始,每个节点都有一个或者多个分支,当然还有没有分支的情况

- 如果数据和数据之间满足一对多的关系,将其逻辑结构称之为树。
- 逻辑关系:树形关系
- 存储关系:顺序存储 链式存储
- 每棵子树的根节点有且仅有一个直接前驱,但是可以有0个或者多个后继。
- 子树:一个结点及其下面的所有结点组成的树。
二、树结点之间的关系
- 根节点:最上层的第一个结点,每棵树有且仅有一个根节点。根节点没有前驱
- 父结点:上一层与自己紧挨着的结点,称之为双亲结点。
- 子结点:下一层与自己紧挨着的结点。
- 兄弟结点:
- 堂兄弟结点:
- 叶子结点:没有子结点的结点
-------------------------------------
- 度:
- 结点的度:该结点的子结点个数。
- 树的度:该树中节点的最大的度
- 层数:
- 根结点的层数是1
- 结点的层数:父结点层数+1
- 深度:
- 从根结点出发,到最底层的层数
举个例子:
上图当中:A称为根,BCD是A的子结点,称A是BCD的父结点,B,C,D之间是兄弟结点,E和G是堂兄弟结点,这个关系可以参考家庭之间的关系
叶子结点(终端结点):比如E,F没有后继结点的结点称为叶子结点
分支结点(非叶子结点):有后继结点,比如G结点
A的度:3 B的度:2 D的度:4 上图树的度:4 上图树的层数:4
A所在层数:1 C所在层数:2
4.有序树与无序树
1.如果将树中结点的各个子树看成是从左往右有次序的(即不能交换),则称该树为有序树,否则称为无序树
森林:多个树组成的一个集合,树之间不存在关系,每棵树都独立存在
如下图三个树的集合:
三、二叉树
二叉树是树的一种特殊形式,即每个分支最多只有两个子结点

1、满二叉树
每个结点的度都为2,即每个结点都有两个子节点,(即二叉树中每个结点的子结点都是满的)

2、完全二叉树
在满二叉树的最底层,最右边,删除n个连续结点,形成的二叉树称之为完全二叉树。
完全二叉树的特点:
- 叶子结点只能出现在最下层和次下层
- 最下层的叶子结点集中在树的左边
- 倒数第2层的叶子结点,一定在右边连续位置
- 满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树
几种常见的完全二叉树:
完全二叉树的编号方式:按照顺序编号
四、二叉树的存储
1、顺序存储
- 二叉树的顺序存储,就是使用一个一维数组存储二叉树结点中的数据,且结点的编号位置就是数组的下标索引。
- 只有在完全二叉树的情况下才能填满数组
- 当为不完全二叉树的时候,会造成大量的空间浪费。所以一般不使用顺序存储。
2、链式存储
- 先序,中序,后序创建。
- 由于是单向链表前者结点可以找到后者结点,但是后者结点不好找前者结点。
- 所以使用先序创建。
结点的表示:
包含了数据域、指向左子树的指针和指向右子树的指针
数据域:存放的数据
指向左子树的指针:存放左子树的地址
指向右子树的指针:存放右子树的地址
使用链式存储方式实现二叉树的创建和遍历,创建如下图的二叉树
//二叉树的应用
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
//创建根节点
struct tree_node
{char date;struct tree_node *left;//左树指针struct tree_node *right;//右树指针
};
//先序创建
//利用递归创建二叉树,返回类型为下一个结点的地址,实现递归创建
struct tree_node * tree_create()
{struct tree_node *node=NULL;//创建一个指针存放节点地址,初始化为空char str;//用来存储创建的数据scanf(" %c",&str);//从终端获取要创建的二叉树if(str=='#')//如果接受到字符#,即这个结点没有return NULL;node=(struct tree_node*)malloc(sizeof(struct tree_node));//新创建的结点if(node==NULL){printf("结点创建失败\n");return NULL;}node->date=str;//递归创建左子树node->left=tree_create();//递归创建右子树node->right=tree_create();return node;
}
//先序遍历
bool tree_erg_fir(struct tree_node *root)
{if(root==NULL){return false;}printf("%c",root->date);tree_erg_fir(root->left);tree_erg_fir(root->right);
}
//中序遍历
bool tree_erg_middle(struct tree_node *root)
{if(root==NULL){return false;}tree_erg_middle(root->left);printf("%c",root->date);tree_erg_middle(root->right);
}
//后序遍历
bool tree_erg_behind(struct tree_node *root)
{if(root==NULL){return false;}tree_erg_behind(root->left);tree_erg_behind(root->right);printf("%c",root->date);
}
int main(int argc, const char *argv[])
{printf("请输入二叉树,创建方式为先序创建:\n");struct tree_node *root=tree_create();//先序遍历tree_erg_fir(root);printf("\n");//中序遍历tree_erg_middle(root);printf("\n");//后序遍历tree_erg_behind(root);printf("\n");return 0;
}
输出如下;
请输入二叉树,创建方式为先序创建:
ABDE###F##CM###
ABDEFCM
EDBFAMC
EDFBMCA
相关文章:

数据结构——树和二叉树
目录 一、树的概念 二、树结点之间的关系 三、二叉树 1、满二叉树 2、完全二叉树 四、二叉树的存储 1、顺序存储 2、链式存储 一、树的概念 如果数据和数据之间满足一对多的关系,将其逻辑结构称之为树 如下图:树的根与树的分支存在一对多的关系 将上…...

142. Go操作Kafka(confluent-kafka-go库)
文章目录 Apache kafka简介开始使用Apache Kafka构建生产者构建消费者 总结 之前已经有两篇文章介绍过 Go如何操作 kafka 28.windows安装kafka,Go操作kafka示例(sarama库) 51.Go操作kafka示例(kafka-go库) Apache ka…...

spring boot(学习笔记第十九课)
spring boot(学习笔记第十九课) Spring boot的batch框架,以及Swagger3(OpenAPI)整合 学习内容: Spring boot的batch框架Spring boot的Swagger3(OpenAPI)整合 1. Spring boot batch框架 Spring Batch是什么 Spring Batch 是一个…...

docker安装 redis 并且加密开启SSL/TLS通道
拉取镜像 docker pull registry.cn-hangzhou.aliyuncs.com/qiluo-images/redis:latest docker tag registry.cn-hangzhou.aliyuncs.com/qiluo-images/redis:latest redis:latest要在 Docker 容器中启动 Redis 并开启 SSL/TLS 加密,需按照以下步骤修改启动命令和配置…...

什么是ARM架构?什么是X86架构?两者的区别是什么?
一、什么是ARM架构 (一)起源于发展 ARM 架构由英国剑桥的 Acorn 计算机公司开发。因市场无合适产品,Acorn 自行设计出第一款微处理器,命名为 ARM。此后 ARM 架构不断发展,1990 年为与苹果合作成立 ARM 公司࿰…...
【vscode】vscode paste image插件设置
本文首发于 ❄️慕雪的寒舍 vscode编辑md文件的时候,如果想插入图片,自带的粘贴只会粘贴到当前目录下,也没有文件重命名,很不友好。 在扩展商店里面有mushan的Paste Image插件,相比自带的,更加友好一点。但…...

自定义string类
#include <iostream> #include <string> int main() { std::string str "Hello, World!"; // 使用 c_str() 将 std::string 转换为 C 风格字符串,并传递给 printf printf("The string is: %s\n", str.c_str()); // 尝试修改…...

Python | Leetcode Python题解之第387题字符串中的第一个唯一字符
题目: 题解: class Solution:def firstUniqChar(self, s: str) -> int:position dict()q collections.deque()n len(s)for i, ch in enumerate(s):if ch not in position:position[ch] iq.append((s[i], i))else:position[ch] -1while q and po…...

RocketMQ 消费时序列化报错问题分析及解决
问题背景 在2024年3月7日,系统消费 RocketMQ 消息时出现了序列化报错,错误信息显示为: java.io.InvalidClassException: com.xxx.xxx.bean.mg.GoodsChangeLogMessage; local class incompatible: stream classdesc serialVersionUID... 这是…...

全能与专精:探索未来AI模型的发展趋势与市场潜力
文章目录 每日一句正能量前言AI模型的全面评估和比较AI模型的专精化和可扩展性AI模型的合理使用和道德规范后记 每日一句正能量 一个人,如果没有经受过投资失败的痛楚,又怎么会看到绝望之后的海阔天空。很多时候,经历了人生中最艰难的事&…...

Python深度学习:【开源数据集系列】ImageNet数据集
ImageNet 是一个大规模的视觉数据集,是计算机视觉领域最重要的基准数据集之一。该数据集由普林斯顿大学和斯坦福大学的研究人员发起,于 2009 年推出。ImageNet 是用于物体分类、目标检测、图像分割、姿势估计等多种任务的通用数据集,尤其在深度学习和计算机视觉的突破性研究…...

微信小程序手写签名
微信小程序手写签名组件 该组件基于signature_pad封装,signature_pad本身是web端的插件,此处将插件代码修改为小程序端可用。 signature_pad.js /*!* Signature Pad v5.0.3 | https://github.com/szimek/signature_pad* (c) 2024 Szymon Nowak | Releas…...

Javascript 使用中点查找矩形的角(Find Corners of Rectangle using mid points)
考虑一个矩形 ABCD,我们给出了边 AD 和 BC 中点(分别为 p 和 q)的坐标以及它们的长度 L(AD BC L)。现在给定参数,我们需要打印 4 个点 A、B、C 和 D 的坐标。 例子: 输入:p (1,…...

【困难】 猿人学web第一届 第18题 jsvmp 洞察先机
文章目录 数据接口分析还原加密参数插桩调试分析日志插桩补充 python 代码 数据接口分析 数据接口 https://match.yuanrenxue.cn/match/18data 请求参数 {page: 页码, t: 时间戳, v: 加密值} 请求第一页不需要携带 t, v 参数 cookie 只需要携带 sessionid 只要 还原加密字段…...

IDEA Maven 源修改为国内阿里云镜像的正确方式
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storm…...

OpenCV 旋转矩形边界
边界矩形是用最小面积绘制的,所以它也考虑了旋转。使用的函数是**cv.minAreaRect**()。 import cv2 import numpy as npimgcv2.imread(rD:\PythonProject\thunder.jpg) img1cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) print(img.dtype) ret,threshcv2.threshold(img1,1…...
人车防撞系统安全生产方案
根据《市场监管总局关于2021~2023年全国特种设备安全状况的通告》数据显示:2023年:全国共发生特种设备事故和相关事故71起,其中死亡69人。包含叉车在内的场(厂)内专用机动车辆事故29起、死亡28人,占事故总数的40.85%、死亡人数的4…...

开放式耳机哪个牌子好?长文传授6招秘籍,彻底远离坑货!
大家好,作为一位专注于评测各类数码产品的博主,今天我特别推荐开放式耳机作为我们日常的首选。这种耳机以其独特的设计,避免了传统耳机长时间佩戴可能带来的不适和感染风险。开放式耳机佩戴简便且稳固,尤其适合热爱跑步和运动的…...

vue2和vue3双向绑定的原理
Vue.js 的双向绑定是 Vue 框架的核心特性之一,它允许数据和视图之间保持同步。虽然 Vue 2 和 Vue 3 都实现了双向绑定,但它们在实现细节上有所不同。 Vue 2 双向绑定的原理 在 Vue 2 中,双向绑定主要依赖于 Object.defineProperty 和观察者…...
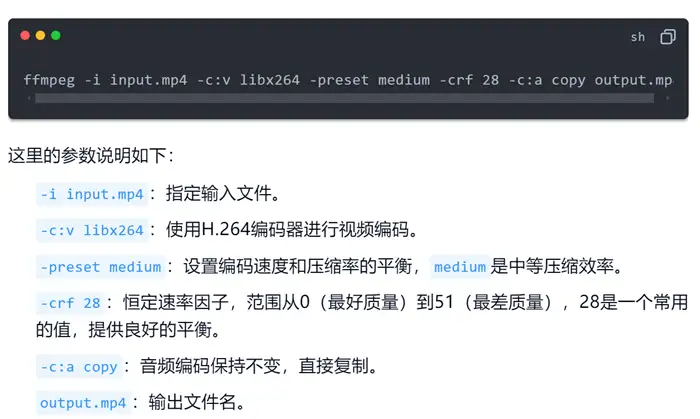
别为大文件烦恼!mp4文件太大怎么变小?3个管用方法
你是否曾经遇到过mp4视频文件过大的困扰?每当想要分享或存储mp4文件时,巨大的文件就成了阻碍。明明感觉感觉没占用多少空间,但是设备却常常出现空间过满警告。 没多少空间的设备真是让人大为恼火,没人想多花一份钱买设备。那么只…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...




