树状数组记录
树状数组(Fenwick Tree)是一种用于维护数组前缀和的数据结构,支持高效的单点更新和区间查询操作。它的查询和更新时间复杂度为 O ( log n ) O(\log n) O(logn),适用于需要频繁更新和查询的场景。
树状数组的基本操作
- 单点更新:将数组中的某个元素增加一个值。
- 前缀和查询:查询数组从起点到某个位置的元素和。
树状数组的实现步骤
- 初始化:创建一个大小为 (n+1) 的数组
tree,初始值为 0。 - 单点更新:更新数组中的某个元素,并相应地更新树状数组。
- 前缀和查询:计算从起点到某个位置的元素和。
以区间和问题举例:

我们有一个数组,即图片中最下面一行的数组,我们也可以理解为,最下面一层是长度为1的区间,倒数第二层是长度为2的区间,然后是长度为4的区间,以此类推,并且区间不重叠。
这个图片展示出来的就是一颗线段树,树状数组是线段树的升级版。我们发现,每一个子树的右半部分可以省略不用。例如要查询[1,3]的区间和,可以通过14+1,而不用通过8+6+1,因此我们可以优化这棵树,得到:

到了这里,树状数组的组成结构基本就结束了,但是这样组织后,怎么确定节点之间的关系?这就要用到lowbit,这是一个十分巧妙的概念。

将剩下的元素组成一个数组后,我们发现,数组每一个位置索引对应的lowbit,就代表了这个位置存储的区间长度。例如我们观察61这个数,索引是16(树状数组索引从1开始),16的lowbit是16(10000->10000),代表61是区间长度为16的区间和,即[1,16],同理,3的索引是9,9的lowbit是1(1001->1),代表9是区间长度为1 [9,9]的区间和。
查询是向前查询
有了这个概念后,查询和更新就很明显了,如果要查询区间[l,r],我们可以查询[0,r]-[0,l],查询方式是:递归减去lowbit,累计数组元素的和,例如计算[1,3],我们先得到索引为3的数值1,然后更新位置 3-lowbit(3)=2,然后从2开始得到14,2-lowbit(2)=0,结束递归,结果为1+14=15。
更新是向后更新
对于更新树状数组的元素,我们需要修改每一个包含了这个元素的所有区间。
与查询不同,修改需要向后修改。如果修改了索引为9的3,我们需要修改9,10,12,16存储的内容。我们发现,与查询相似,可以通过+lowbit来得到包含自己的更大的区间,例如:9+lowbit(9)=10, 10+lowbit(10)=12, 12+lowbit(12) = 16,因此我们同样使用递归,直到索引到达数组长度上限。
区间异或问题
#include<bits/stdc++.h>using namespace std;typedef long long ll;int t[300005];
int a[300005];
int n, q;inline int lowbit(int x) {return x & -x;
}int get(int x) {int res = 0;for (int i = x; i; i -= lowbit(i)) {res ^= t[i];}return res;
}void add(int x, int y) {for (int i = x; i <= n; i += lowbit(i)) {t[i] ^= y;}
}int range_get(int l, int r) {return get(r) ^ get(l - 1);
}int main(){cin >> n >> q;for(int i = 1; i <= n; i++){cin >> a[i];add(i, a[i]);}while(q--){int op, x, y;cin >> op >> x >> y;if(op == 1){add(x, y);}else{cout << range_get(x, y) << endl;}}
}
相关文章:

树状数组记录
树状数组(Fenwick Tree)是一种用于维护数组前缀和的数据结构,支持高效的单点更新和区间查询操作。它的查询和更新时间复杂度为 O ( log n ) O(\log n) O(logn),适用于需要频繁更新和查询的场景。 树状数组的基本操作 单点更…...
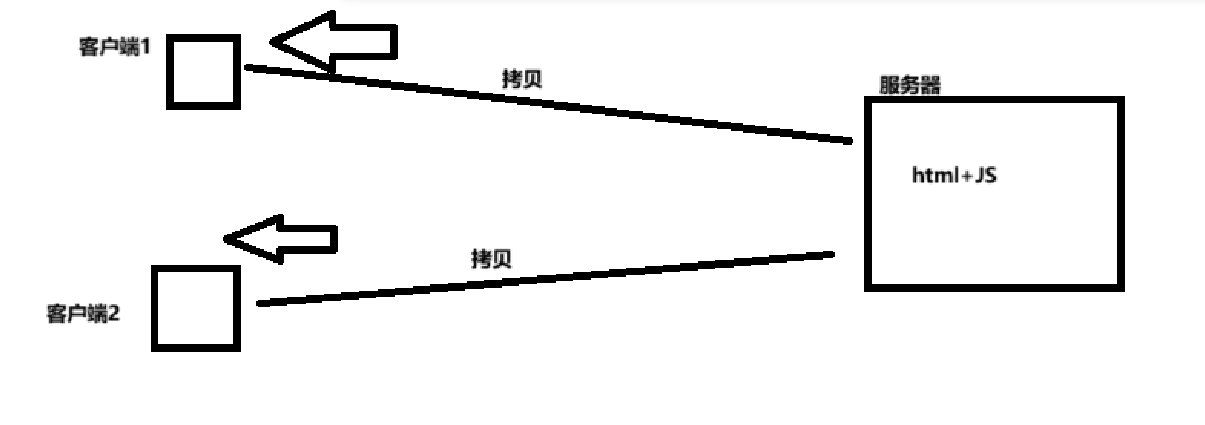
客户端时间和服务器时间的区别
客户端时间: 服务器向客户端拷贝一份前端内容,客户端通过JS获取时间,这样获取的是客户端时间 服务器时间: 服务器通过java代码获取的时间传输给客户端,这样获取的是服务器时间 当有些时候需要使用客户端时间…...

已入职华为!!关于我成功拿下华为大模型算法岗经验总结
方向:大模型算法工程师 整个面试持续了1小时10分钟,能够看出面试官是典型搞技术的,问的很专业又很细,全程感觉压力好大,面完后感觉丝丝凉意,不过幸好还是成功拿下了Offer 一面: 自我介绍 简历项目深度交流 1.项目的背…...

从安卓开发到AI产品经理——我的AI绘画之旅
大家好,我是一名有着多年安卓开发经验的程序员。在日复一日的编码生活中,我对AI行业产生了浓厚的兴趣。于是,我决定转行成为一名AI产品经理。在这个过程中,我通过学习AI绘画工具初步了解了AI行业,下面我将分享我的学习…...

代码随想录八股训练营第三十四天| C++
前言 一、vector和list的区别? 1.1.存储方式: 1.2.随机访问: 1.3.插入和删除操作: 1.4.内存使用: 1.5.容量和大小: 1.6.迭代器类型: 1.7.用途: 二、vector 底层原理和扩容过…...

《深入理解 Java 中的 this 关键字》
目录 一、this关键字的基本理解 二、this调用属性和方法 (一)一般情况 (二)特殊情况 三、this调用构造器 四、案例分析 (一)Account类 (二)Customer类 (三&…...

python文件自动分类(5)
完成了文件自动分类的操作后,我们一起来复习下: 首先,获取文件夹中所有文件名称,用 os.path.join() 函数拼接出要移动到的目标地址。然后,使用 os.path.exists() 函数判断目标文件夹是否存在,不存在用 os.m…...

【Unity-Lua】音乐播放器循环滚动播放音乐名
前言:Unity中UI节点 图1 如上所示,一开始本来是打算用ScrollView做的,觉得直接计算对应的文本位置就行,所以没用ScrollRect来做,可以忽略Scroll,Viewport这些名字。如下图:需要在一个背景Image…...

宏碁扩展Swift系列,推出四款全新AI笔记本电脑
Acer正在扩展其Swift笔记本产品线,推出四款新型号,每款都内置了AI功能。这些笔记本提供诸如Microsoft Copilot、Acer用户感应技术、Windows Studio效应、PurifiedVoice 2.0和PurifiedView等功能。其他功能还包括Wi-Fi 7和Bluetooth 5.4连接。 我们先来看…...

科研绘图系列:R语言差异基因四分图(Quad plot)
文章目录 介绍加载R包导入数据数据预处理画图参考介绍 四分图(Quad plot)是一种数据可视化技术,通常用于展示四个变量之间的关系。它由四个子图组成,每个子图都显示两个变量之间的关系。四分图的布局通常是2x2的网格,每个格子代表一个变量对的散点图。 在四分图中,通常…...

文字或图案点选坐标点返回
最近看到这篇文章中讲到极验图片验证码破解方案 https://blog.geetest.com/article/65aaaa944edc5ec343ba9f52efef0cdc 其中核心解决步骤如下,作者还贴心的贴出了CNN代码,真是用心良极: step 3:批量下载存储验证图片,…...

硬盘数据恢复软件TOP4榜单出炉,选对方法竟然如此重要
这年头,信息多得不得了,数据对我们来说太重要了。但是,不管是咱们自己还是公司,都可能碰上丢数据的倒霉事,特别是不小心把硬盘里的东西删了。数据一丢,不光可能亏钱,工作和生活也可能受影响。好…...

给自己复盘用的随想录笔记-栈与队列
用栈实现队列 难在出去 232. 用栈实现队列 - 力扣(LeetCode) class MyQueue {private Stack<Integer> A;private Stack<Integer> B;public MyQueue() {Anew Stack<>();Bnew Stack<>();}public void push(int x) {A.push(x);}pu…...

微信小程序跳转到另一个微信小程序
引用:http://www.xmdeal.com/mobanjiaocheng/254.html 第一种方法: wx.navigateToMiniProgram 官方文档:https://developers.weixin.qq.com/miniprogram/dev/api/navigate/wx.navigateToMiniProgram.html wx.navigateToMiniProgram({appId…...

【知识图谱】4、LLM大模型结合neo4j图数据库实现AI问答的功能
昨天写了一篇文章,使用fastapi直接操作neo4j图数据库插入数据的例子, 本文实现LLM大模型结合neo4j图数据库实现AI问答功能。 废话不多说,先上代码 import gradio as gr from fastapi import FastAPI, HTTPException, Request from pydantic…...

《信息技术 云计算 边缘云通用技术要求》国家标准发布,九州未来参编
日前,2024年第17号国家标准公告发布,由全国信标委云计算标准工作组组织制定、九州未来作为行业专家单位参编的《信息技术 云计算 边缘云通用技术要求》国家标准正式获批发布。 边缘云作为云计算技术的有效补充和拓展,能够实现将云计算能力拓展…...
NTFS硬盘支持工具Paragon NTFS for Mac 15.4.44 中文破解版
Paragon NTFS for Mac 15.4.44 中文破解版是一个底层的文件系统驱动程序,专门开发用来弥合Windows和Mac OS X之间的不兼容性,通过在Mac OS X系统下提供对任何版本的NTFS文件系统完全的读写访问服务来弥合这种不兼容性。为您轻松解决Mac不能识别Windows NTFS文件难题…...

66-java 类型擦除
类型擦除是Java类型信息在运行时的一个特性,它发生在泛型类型被擦除成它们的原始类型后,以及在运行时,由于类型擦除,泛型信息不可用。 例如,以下两个泛型类型: List<String> list1 new ArrayList&…...

25考研人数预计下降?这一届考研有哪些新趋势?
2025年考研时间线: 2024年9月:公共课及各院校考试大纲公布; 2024年9月下旬:预报名; 2024年10月:正式报名; 2024年11月:线上/线下确认; 2024年12月中下旬:…...

比尔·盖茨对AI充满信心
The Verge与比尔盖茨进行了关于AI、错误信息和气候变化的对话。 比尔盖茨花费数十亿美元资助他认为将塑造未来的技术——从应对气候变化到消灭疾病。 盖茨在一部新的Netflix系列片《未来之路:比尔盖茨的境界》中深入探讨了这些话题。该系列于9月18日首播ÿ…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...
