KMP 详解
KMP数组存的是什么
对于一个字符串 b,下标从1开始。
则kmp[i]表示 以i结尾的连续子串 = s的前缀的最大值(等价于前缀最大结尾处)
如何求KMP
假设 i 以前的KMP都被求出来了。
j 表示上一个字符可以成功匹配的长度(等价于下标)
如果b[j+1] != b[i]下一个位置匹配不上(即不能成为前缀)
则,让j = kmp[j] 即成为以j结尾的 连续子串 的 最长前缀 尾部的下标
退出循环后,若还能匹配上则j++(本质是,加上i的贡献。因为j = 0时可能匹配不上)
然后让kmp[i] = j即可。
运用kmp
和求kmp差不多,如果匹配不上,求让a[i]和以j结尾的连续子串的最长前缀匹配。(放宽要求)
算法正确性证明
用哲学的话来说就是,每一次失败都会让我变得更强大。
当匹配不上时,匹配串b至少会前移1位,由指针的思想。O(n)可证。
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+7;
int kmp[N];
string a,b;
int j;
int main(){cin>>a>>b;a = " "+a;b = " "+b;for(int i = 2;i < b.size();i++){while(j&&b[j+1] != b[i]){j = kmp[j];}if(b[j+1] == b[i])j++;kmp[i] = j;}j = 0;for(int i = 1;i < a.size();i++){while(j&&a[i] != b[j+1]){j = kmp[j];}if(b[j+1] == a[i])j++;if(j == b.size()-1){cout<<i-(b.size()-1)+1<<endl;j=kmp[j];}}for (int i=1;i < b.size();i++)cout<<kmp[i]<<" ";return 0;
} 
相关文章:

KMP 详解
KMP数组存的是什么 对于一个字符串 b,下标从1开始。 则kmp[i]表示 以i结尾的连续子串 s的前缀的最大值(等价于前缀最大结尾处) 如何求KMP 假设 i 以前的KMP都被求出来了。 j 表示上一个字符可以成功匹配的长度(等价于下标) …...

go语言并发编程-超详细mutex解析
文章目录 1 go语言并发编程学习-mutex1.1 学习过程1.2 如何解决资源并发访问的问题?【基本用法】1.2.1 并发访问带来的问题1.2.1.1 导致问题的原因 1.2.2 race detector检查data race1.2.3 mutex的基本实现机制以及使用方法1.2.3.1 具体使用-11.2.3.1 具体使用-2 1 …...

VirtualBox Debian 自动安装脚本
概览 相较于原脚本(安装目录/UnattendedTemplates/debian_pressed.cfg)更新如下内容: 配置清华镜像源配置仅主机网卡(后续只需添加仅主机网卡即可)配置Root用户远程登录配置用户sudo组 脚本 debian_pressed.cfg ##…...
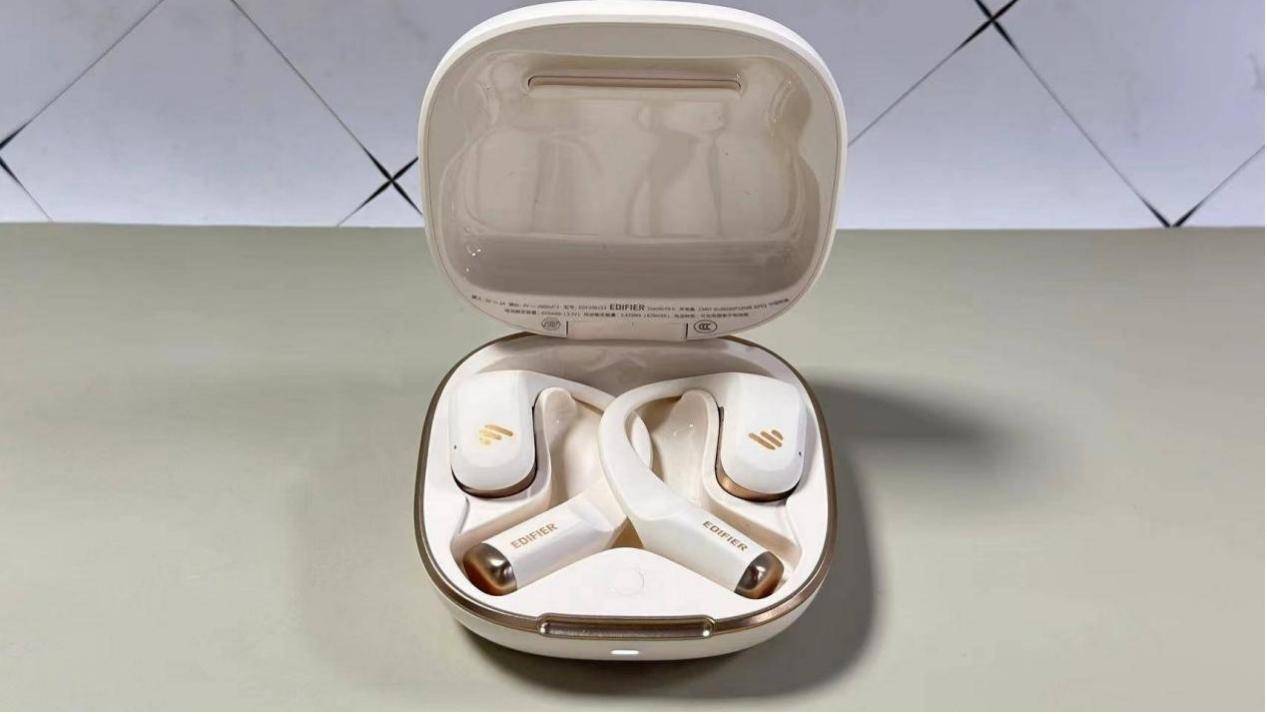
最好的开放式耳机?五款红榜开放式耳机推荐!
面对众多的开放式耳机选项,消费者可能会感到难以抉择。买耳机不一定要买最贵最好的,但是一定要选最适合自己的,为了使选择过程更加容易,我提供了一些建议,推荐了几款既适合日常使用又佩戴舒适的热门开放式耳机。 开放式…...

线性代数之线性方程组
目录 线性方程组 1. 解的个数 齐次线性方程组: 非齐次线性方程组: 2. 齐次线性方程组的解 3. 非齐次线性方程组的解 4. 使用 Python 和 NumPy 求解线性方程组 示例代码 齐次线性方程组 非齐次线性方程组 示例结果 齐次线性方程组 非齐次线性…...

速盾:怎么查看是否使用cdn服务?
CDN(Content Delivery Network),即内容分发网络,是一种加速网络内容传输的技术。通过在全球各地建立分布式的节点服务器,将网站的静态资源缓存到最近的节点服务器上,使用户可以从离自己地理位置最近的节点服…...
828华为云征文|采用Flexus云服务器X实例部署RTSP直播服务器
一、前言 这篇文章讲解: 采用华为云最新推出的Flexus云服务器X实例搭建RTSP服务器,完成视频直播需求。 随着实时视频流传输需求的增长,RTSP(实时流协议)服务器成为了许多视频监控、直播和多媒体应用的核心组件。在当…...
)
Spring Cloud Gateway(二)
Spring Cloud Gateway(二) 文章目录 Spring Cloud Gateway(二)Gateway工作原理为什么使用API网关高并发Gateway性能优化 Gateway工作原理 Spring Cloud Gateway旨在为微服务架构提供简单、有效并且统一的API路由管理方式。它不仅…...

docker 简易入门
# docker 简易入门 docker由几个组成部分 docker client: 即 docker 命令行工具 docker host: 宿主机,docker daemon 的运行环境服务器 docker daemon: docker 的守护进程,docker client 通过命令行与 docker daemon 交互 container: 最小型的一个操…...

【看雪-注册安全分析报告】
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 暴力破解密码,造成用户信息泄露短信盗刷的安全问题,影响业务及导致用户投诉带来经济损失,尤其是后付费客户,风险巨大,造成亏损无底洞…...

记录一个前端学习小组的收集的模版
问题1:输入“您的姓名”,选择“短答案”作为问题类型。问题2:输入“您是否愿意继续参加前端学习小组?”,选择“单选”作为问题类型,并添加选项“是”和“否”。问题3:输入“如果您选择‘是’&am…...

Rk3588 Android12 AIDL 开发
AIDL (Android Interface Definition Language) 和 HIDL (HAL Interface Definition Language) 都是 Android 系统中用于定义接口的工具,但它们有不同的用途和特性。 AIDL (Android Interface Definition Language) 用途: 主要用于应用程序之间的进程间…...
)
两个长整数字符串求和(不允许使用ES6+)
两个长整数字符串求和(不允许使用ES6), 面试手撸代码遇到到这个问题 1. 实现方式第一种 // 短整数字符串前边补 0; num需要补 0 的短整数字符串, len 长整数字符串的长度 function fillZero (num, len) {let str num.toString();if (str.length < len) {str 0.repeat(…...

11 Java 方法引用、异常处理、Java接口之函数式编程(接口知识补充Function<T,R>、BiFunction<T, U, R>和自定义泛型接口)
文章目录 前言一、Java接口之函数式编程 --- 接口知识补充1 Function<T,R>泛型接口2 BiFunction<T, U, R>泛型接口3 自定义泛型函数式编程接口4 使用lambda表达式、方法引用进行函数式编程二、方法引用1 方法引用初体验(以Array.sort()方法为例)(1)什么是方法引…...

深入探索 Go 语言的编译器与垃圾回收机制
Go 编译器 Go 编译器是通过 go 工具执行的,这个工具的功能不仅仅是生成可执行文件。你可以使用 go tool compile 命令来编译一个 Go 源文件。这个操作将生成一个目标文件,也就是 .o 后缀的文件。以下是在 macOS Mojave 系统上执行的命令和结果展示&…...
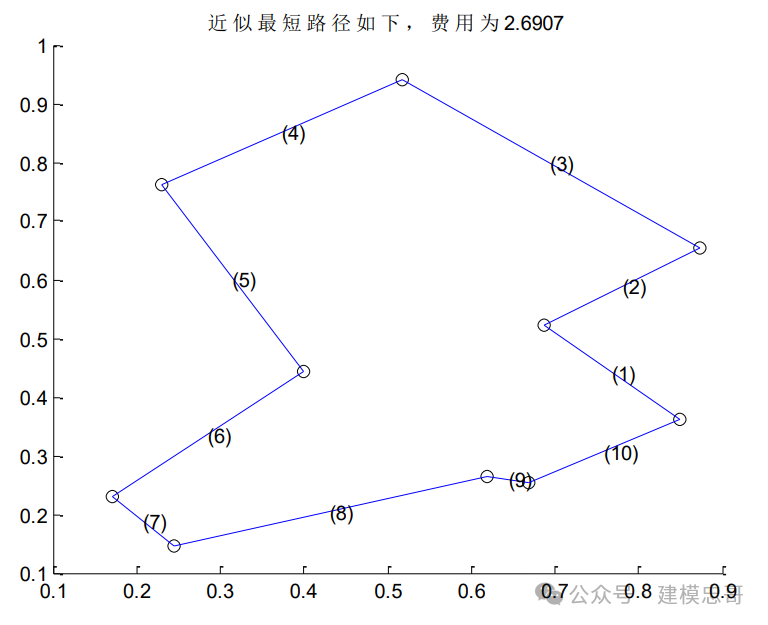
2024国赛数学建模-模拟火算法(MATLAB 实现)
模拟退火算法 1.1 算法原理 模拟退火算法的基本思想是从一给定解开始 ,从邻域 中随机产生另一个解 ,接受 Metropolis准则允许目标函数在 有限范围内变坏 ,它由一控制参数 t决定 ,其作用类似于物 理过程中的温度 T,对于控制参数的每一取值 ,算法持续进 行“产生 —判断 —接受…...

YOLOv8 只检测人 只画框不要标签
参考了这个:YOLOv8只检测人(或其他一种或者多种类别)_yolov8只检测指定类别-CSDN博客 1. 只检测人:predict的时候指定参数classes[0] 2. 只画框不要标签:plot的时候传入labelsFalse 3. 标签中去掉置信度:…...

如何将网络安全防范游戏化
组织对威胁的准备和恢复能力跟不上网络犯罪分子的进步。 一些首席执行官仍然认为网络安全需要偶尔干预,而不是持续关注。 但对于许多公司来说,情况并非如此;网络威胁准备需要协调一致的培训工作,因此网络安全团队在攻击发生时已…...

Qt QGraphicsView实现图片放缩、鼠标拖动移动、鼠标点位置放大缩小_图片查看
QtQGraphicsView实现图片放缩、鼠标拖动移动、鼠标点位置放大缩小 头文件: #ifndef TIMGWIDGET_H #define TIMGWIDGET_H#include <QGraphicsItem> #include <QMainWindow> #include <QObject> #include <QWidget>// class TImgWidget : pu…...

Percona Toolkit 神器全攻略(复制类)
Percona Toolkit 神器全攻略(复制类) Percona Toolkit 神器全攻略系列共八篇,前文回顾: 前文回顾Percona Toolkit 神器全攻略Percona Toolkit 神器全攻略(实用类)Percona Toolkit 神器全攻略(配…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...

Easy Excel
Easy Excel 一、依赖引入二、基本使用1. 定义实体类(导入/导出共用)2. 写 Excel3. 读 Excel 三、常用注解说明(完整列表)四、进阶:自定义转换器(Converter) 其它自定义转换器没生效 Easy Excel在…...
