线性代数之线性方程组
目录
线性方程组
1. 解的个数
齐次线性方程组:
非齐次线性方程组:
2. 齐次线性方程组的解
3. 非齐次线性方程组的解
4. 使用 Python 和 NumPy 求解线性方程组
示例代码
齐次线性方程组
非齐次线性方程组
示例结果
齐次线性方程组
非齐次线性方程组
线性方程组
1. 解的个数
-
齐次线性方程组:
- 只有零解:当系数矩阵的秩等于未知量的个数 𝑛n 时,即 rank(𝐴)=𝑛rank(A)=n。
- 有非零解:当系数矩阵的秩小于未知量的个数 𝑛n 时,即 rank(𝐴)<𝑛rank(A)<n。

-
非齐次线性方程组:
- 无解:当增广矩阵的秩不等于系数矩阵的秩,即 rank([𝐴∣𝑏])≠rank(𝐴)rank([A∣b])=rank(A)。
- 有解:
- 唯一解:当增广矩阵的秩等于系数矩阵的秩且等于未知量的个数 𝑛n,即 rank([𝐴∣𝑏])=rank(𝐴)=𝑛rank([A∣b])=rank(A)=n。
- 无穷多解:当增广矩阵的秩等于系数矩阵的秩但小于未知量的个数 𝑛n,即 rank([𝐴∣𝑏])=rank(𝐴)<𝑛rank([A∣b])=rank(A)<n。

2. 齐次线性方程组的解
- 基础解系:齐次线性方程组的基础解系是指一组线性无关的解向量,使得所有解都能表示为这些向量的线性组合。
- 求解步骤:
- 化简系数矩阵:将系数矩阵 𝐴A 化简为行阶梯形或行最简形。
- 列出方程:根据化简后的矩阵列出相应的方程。
- 确定自由未知量:找出方程组中的自由未知量(即那些不是其他未知量表达式的未知量)。
- 令自由未知量为线性无关组:设自由未知量为任意实数,并保证它们之间线性无关。
- 得到基础解系:利用自由未知量表达出其他未知量的解,从而得到基础解系。
- 写出一般解:将基础解系的解向量按自由未知量的不同取值线性组合,得到方程组的一般解。
3. 非齐次线性方程组的解
- 解的结构:非齐次线性方程组的解集可以表示为一个特解加上齐次方程组的所有解。
- 求解步骤:
- 求特解:通过数值方法或符号计算求出一个特解 𝑥𝑝xp。
- 求齐次方程组的基础解系:求出对应的齐次方程组 𝐴𝑥=0Ax=0 的基础解系。
- 写出一般解:一般解可以表示为 𝑥=𝑥𝑝+𝑐1𝑣1+𝑐2𝑣2+…+𝑐𝑘𝑣𝑘x=xp+c1v1+c2v2+…+ckvk,其中 𝑣𝑖vi 是齐次方程组的基础解系中的解向量。
4. 使用 Python 和 NumPy 求解线性方程组
齐次线性方程组:
- 通常用于求解特征值问题,例如求解特征向量。
- 使用
numpy.linalg.eig()函数求解特征值和特征向量。非齐次线性方程组:
- 用于确定未知量的值。
- 使用
numpy.linalg.solve()函数求解未知量。
下面分别给出齐次和非齐次线性方程组的例子,我们将使用 Python 和 NumPy 来求解这些例子。
示例代码
齐次线性方程组
import numpy as np# 定义系数矩阵 A
A = np.array([[3, 1], [1, 3]])# 使用 numpy.linalg.eig() 求解特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(A)print("Eigenvalues:", eigenvalues)
print("Eigenvectors:", eigenvectors)非齐次线性方程组
import numpy as np# 定义系数矩阵 A 和右侧向量 b
A = np.array([[2, -1, 0], [-1, 2, -1], [0, -1, 2]])
b = np.array([1, 0, -1])
6
# 使用 numpy.linalg.solve() 求解未知量
x = np.linalg.solve(A, b)print("Solution x:", x)调用过程
import numpy as np
# 齐次线性方程组示例
# 定义系数矩阵 A
A_homogeneous = np.array([[3, 1], [1, 3]])# 使用 numpy.linalg.eig() 求解特征值和特征向量
eigenvalues_homogeneous, eigenvectors_homogeneous = np.linalg.eig(A_homogeneous)# 非齐次线性方程组示例
# 定义系数矩阵 A 和右侧向量 b
A_inhomogeneous = np.array([[2, -1, 0], [-1, 2, -1], [0, -1, 2]])
b_inhomogeneous = np.array([1, 0, -1])
# 使用 numpy.linalg.solve() 求解未知量
x_inhomogeneous = np.linalg.solve(A_inhomogeneous, b_inhomogeneous)
eigenvalues_homogeneous, eigenvectors_homogeneous, x_inhomogeneous调用结果
(array([4., 2.]),
array([[ 0.70710678, -0.70710678],[ 0.70710678, 0.70710678]]),
array([ 0.5, 0. , -0.5]))示例结果
齐次线性方程组
- 特征值:
Eigenvalues: [4. 2.] - 特征向量:
Eigenvectors: [[ 0.70710678 -0.70710678][ 0.70710678 0.70710678]]
非齐次线性方程组
- 解:
Solution x: [ 0.5 0. -0.5]
从上面的结果可以看出:
- 对于齐次线性方程组,我们得到了两个特征值 4 和 2,以及对应的特征向量。特征向量代表了齐次方程组的解向量。
- 对于非齐次线性方程组,我们得到了未知量 𝑥x 的解为 [0.5,0,−0.5][0.5,0,−0.5]。
相关文章:

线性代数之线性方程组
目录 线性方程组 1. 解的个数 齐次线性方程组: 非齐次线性方程组: 2. 齐次线性方程组的解 3. 非齐次线性方程组的解 4. 使用 Python 和 NumPy 求解线性方程组 示例代码 齐次线性方程组 非齐次线性方程组 示例结果 齐次线性方程组 非齐次线性…...

速盾:怎么查看是否使用cdn服务?
CDN(Content Delivery Network),即内容分发网络,是一种加速网络内容传输的技术。通过在全球各地建立分布式的节点服务器,将网站的静态资源缓存到最近的节点服务器上,使用户可以从离自己地理位置最近的节点服…...
828华为云征文|采用Flexus云服务器X实例部署RTSP直播服务器
一、前言 这篇文章讲解: 采用华为云最新推出的Flexus云服务器X实例搭建RTSP服务器,完成视频直播需求。 随着实时视频流传输需求的增长,RTSP(实时流协议)服务器成为了许多视频监控、直播和多媒体应用的核心组件。在当…...
)
Spring Cloud Gateway(二)
Spring Cloud Gateway(二) 文章目录 Spring Cloud Gateway(二)Gateway工作原理为什么使用API网关高并发Gateway性能优化 Gateway工作原理 Spring Cloud Gateway旨在为微服务架构提供简单、有效并且统一的API路由管理方式。它不仅…...

docker 简易入门
# docker 简易入门 docker由几个组成部分 docker client: 即 docker 命令行工具 docker host: 宿主机,docker daemon 的运行环境服务器 docker daemon: docker 的守护进程,docker client 通过命令行与 docker daemon 交互 container: 最小型的一个操…...

【看雪-注册安全分析报告】
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 暴力破解密码,造成用户信息泄露短信盗刷的安全问题,影响业务及导致用户投诉带来经济损失,尤其是后付费客户,风险巨大,造成亏损无底洞…...

记录一个前端学习小组的收集的模版
问题1:输入“您的姓名”,选择“短答案”作为问题类型。问题2:输入“您是否愿意继续参加前端学习小组?”,选择“单选”作为问题类型,并添加选项“是”和“否”。问题3:输入“如果您选择‘是’&am…...

Rk3588 Android12 AIDL 开发
AIDL (Android Interface Definition Language) 和 HIDL (HAL Interface Definition Language) 都是 Android 系统中用于定义接口的工具,但它们有不同的用途和特性。 AIDL (Android Interface Definition Language) 用途: 主要用于应用程序之间的进程间…...
)
两个长整数字符串求和(不允许使用ES6+)
两个长整数字符串求和(不允许使用ES6), 面试手撸代码遇到到这个问题 1. 实现方式第一种 // 短整数字符串前边补 0; num需要补 0 的短整数字符串, len 长整数字符串的长度 function fillZero (num, len) {let str num.toString();if (str.length < len) {str 0.repeat(…...

11 Java 方法引用、异常处理、Java接口之函数式编程(接口知识补充Function<T,R>、BiFunction<T, U, R>和自定义泛型接口)
文章目录 前言一、Java接口之函数式编程 --- 接口知识补充1 Function<T,R>泛型接口2 BiFunction<T, U, R>泛型接口3 自定义泛型函数式编程接口4 使用lambda表达式、方法引用进行函数式编程二、方法引用1 方法引用初体验(以Array.sort()方法为例)(1)什么是方法引…...

深入探索 Go 语言的编译器与垃圾回收机制
Go 编译器 Go 编译器是通过 go 工具执行的,这个工具的功能不仅仅是生成可执行文件。你可以使用 go tool compile 命令来编译一个 Go 源文件。这个操作将生成一个目标文件,也就是 .o 后缀的文件。以下是在 macOS Mojave 系统上执行的命令和结果展示&…...
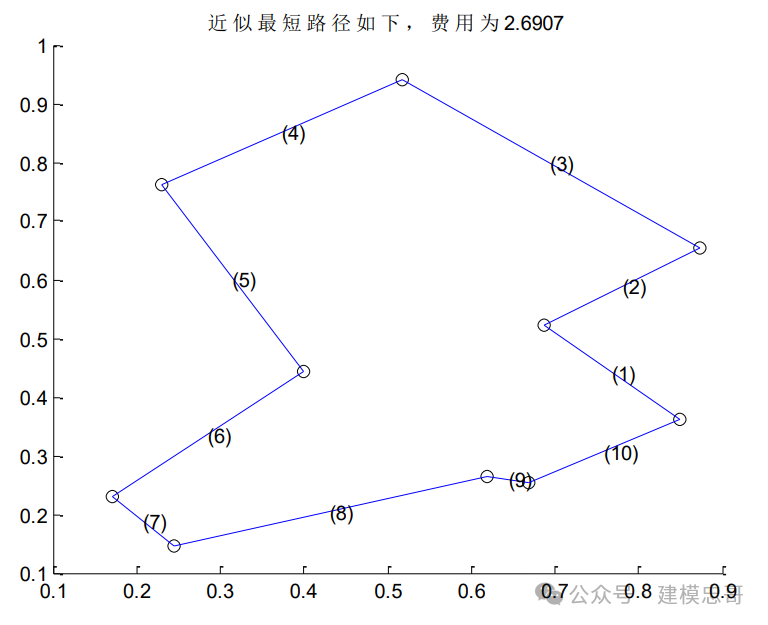
2024国赛数学建模-模拟火算法(MATLAB 实现)
模拟退火算法 1.1 算法原理 模拟退火算法的基本思想是从一给定解开始 ,从邻域 中随机产生另一个解 ,接受 Metropolis准则允许目标函数在 有限范围内变坏 ,它由一控制参数 t决定 ,其作用类似于物 理过程中的温度 T,对于控制参数的每一取值 ,算法持续进 行“产生 —判断 —接受…...

YOLOv8 只检测人 只画框不要标签
参考了这个:YOLOv8只检测人(或其他一种或者多种类别)_yolov8只检测指定类别-CSDN博客 1. 只检测人:predict的时候指定参数classes[0] 2. 只画框不要标签:plot的时候传入labelsFalse 3. 标签中去掉置信度:…...

如何将网络安全防范游戏化
组织对威胁的准备和恢复能力跟不上网络犯罪分子的进步。 一些首席执行官仍然认为网络安全需要偶尔干预,而不是持续关注。 但对于许多公司来说,情况并非如此;网络威胁准备需要协调一致的培训工作,因此网络安全团队在攻击发生时已…...

Qt QGraphicsView实现图片放缩、鼠标拖动移动、鼠标点位置放大缩小_图片查看
QtQGraphicsView实现图片放缩、鼠标拖动移动、鼠标点位置放大缩小 头文件: #ifndef TIMGWIDGET_H #define TIMGWIDGET_H#include <QGraphicsItem> #include <QMainWindow> #include <QObject> #include <QWidget>// class TImgWidget : pu…...

Percona Toolkit 神器全攻略(复制类)
Percona Toolkit 神器全攻略(复制类) Percona Toolkit 神器全攻略系列共八篇,前文回顾: 前文回顾Percona Toolkit 神器全攻略Percona Toolkit 神器全攻略(实用类)Percona Toolkit 神器全攻略(配…...

SQLite3 数据类型深入全面讲解
SQLite3,作为一款轻量级的数据库管理系统,在数据存储方面展现出了其独特的魅力。它不仅支持标准的SQL语法,还提供了丰富的数据类型供开发者选择。这些数据类型不仅涵盖了基本的数值和文本类型,还包括了日期时间、二进制数据等复杂…...
及其插入和查找操作)
Python高效实现Trie(前缀树)及其插入和查找操作
Python高效实现Trie(前缀树)及其插入和查找操作 在Python面试中,考官通常会关注候选人的编程能力、问题解决能力以及对Python语言特性的理解。Trie(前缀树)是一种高效的数据结构,广泛应用于字符串处理、自动补全、拼写检查等场景。本文将详细介绍如何实现一个Trie,并提…...

傅里叶变换家族
禹晶、肖创柏、廖庆敏《数字图像处理(面向新工科的电工电子信息基础课程系列教材)》 禹晶、肖创柏、廖庆敏《数字图像处理》资源二维码...

深度学习——强化学习算法介绍
强化学习算法介绍 强化学习讨论的问题是一个智能体(agent) 怎么在一个复杂不确定的环境(environment)里面去极大化它能获得的奖励。 强化学习和监督学习 强化学习有这个试错探索(trial-and-error exploration),它需要通过探索环境来获取对环境的理解。强化学习 ag…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
