当前位置： 首页 > news >正文

Python高效实现Trie（前缀树）及其插入和查找操作

news 2026/2/7 10:31:34

Python高效实现Trie（前缀树）及其插入和查找操作

在Python面试中，考官通常会关注候选人的编程能力、问题解决能力以及对Python语言特性的理解。Trie（前缀树）是一种高效的数据结构，广泛应用于字符串处理、自动补全、拼写检查等场景。本文将详细介绍如何实现一个Trie，并提供插入和查找操作，确保代码实用性强，条理清晰，操作性强。

1. 引言

Trie（前缀树）是一种树形数据结构，用于高效地存储和检索字符串集合中的键。与其他树形数据结构不同，Trie的节点不存储键本身，而是存储键的前缀。每个节点的子节点表示具有相同前缀的不同可能后续字符。Trie的主要操作包括插入（insert）和查找（search）。

2. Trie的基本结构

Trie由节点组成，每个节点包含以下属性：

  • children：一个字典，键为字符，值为对应的子节点。
  • is_end_of_word：一个布尔值，表示该节点是否是某个单词的结尾。

以下是Trie节点的定义：

<

相关文章：

Python高效实现Trie（前缀树）及其插入和查找操作

Python高效实现Trie（前缀树）及其插入和查找操作 在Python面试中，考官通常会关注候选人的编程能力、问题解决能力以及对Python语言特性的理解。Trie（前缀树）是一种高效的数据结构，广泛应用于字符串处理、自动补全、拼写检查等场景。本文将详细介绍如何实现一个Trie，并提…...

编程日记 2024/9/6 13:42:50

傅里叶变换家族

禹晶、肖创柏、廖庆敏《数字图像处理&#xff08;面向新工科的电工电子信息基础课程系列教材&#xff09;》 禹晶、肖创柏、廖庆敏《数字图像处理》资源二维码...

编程日记 2024/9/6 13:41:49

深度学习——强化学习算法介绍

强化学习算法介绍 强化学习讨论的问题是一个智能体(agent) 怎么在一个复杂不确定的环境(environment)里面去极大化它能获得的奖励。 强化学习和监督学习 强化学习有这个试错探索(trial-and-error exploration)&#xff0c;它需要通过探索环境来获取对环境的理解。强化学习 ag…...

编程日记 2024/9/6 13:40:48

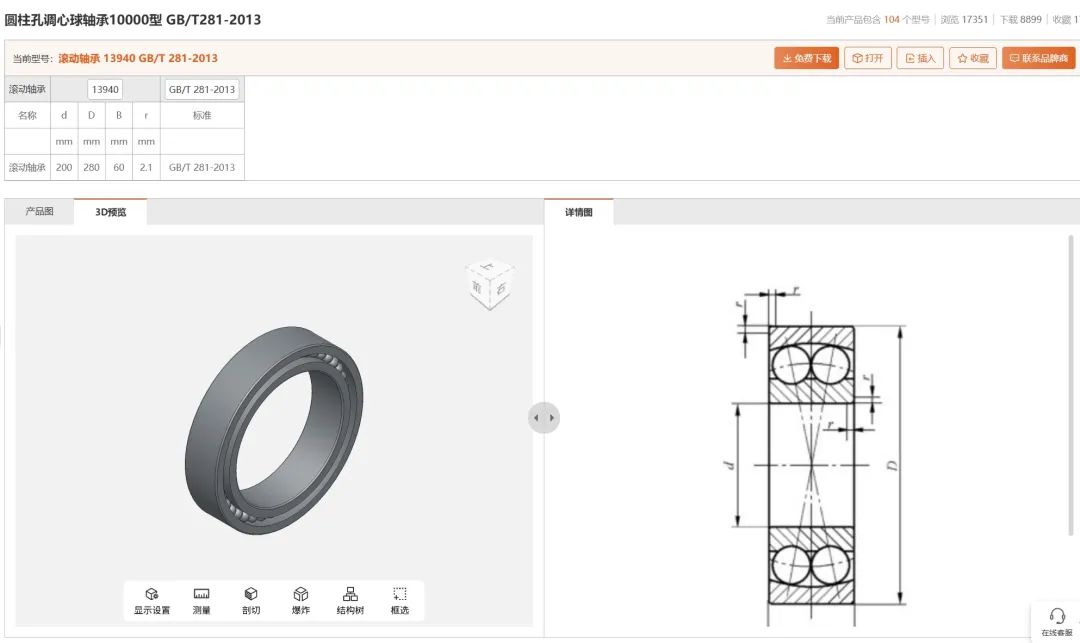
轴承知识大全，详细介绍（附3D图纸免费下载）

轴承一般由内圈、外圈、滚动体和保持架组成。对于密封轴承&#xff0c;再加上润滑剂和密封圈&#xff08;或防尘盖&#xff09;。这就是轴承的全部组成。 根据轴承使用的工作状况来选用不同类型的轴承&#xff0c;才能更好的发挥轴承的功能&#xff0c;并延长轴承的使用寿命。我…...

编程日记 2024/9/6 13:37:45

【PyTorch】基础环境如何打开

前期安装可以基于这个视频&#xff0c;本文是为了给自己存档如何打开pycharm和jupyter notebookPyTorch深度学习快速入门教程&#xff08;绝对通俗易懂&#xff01;&#xff09;【小土堆】_哔哩哔哩_bilibili Pycharm 配置 新建项目的时候选择解释器pytorch-gpu即可。 Jupyte…...

编程日记 2024/9/6 13:36:44

QT教程：QTime和QTimer的使用场景

QTime类 QTime 是一个用来表示和操作时间的类&#xff0c;它处理一天中的具体时间&#xff08;例如小时、分钟、秒、毫秒&#xff09;。通常用于计算时间间隔、记录时间戳、获取当前时间等。 特点和功能 表示时间&#xff1a;QTime 用来表示一天中的某个具体时间&#xff08;小…...

编程日记 2024/9/6 13:35:43

MySQL 迁移中 explicit_defaults_for_timestamp 参数影响

前言 最近在做数据迁移的时候&#xff0c;使用的是云平台自带的同步工具&#xff0c;在预检查阶段&#xff0c;当时报错 explicit_defaults_for_timestamp 参数在目标端为 off 建议修改 on&#xff0c;有什么风险呢&#xff1f;在此记录下。 测试对比 MySQL 默认情况下 expl…...

编程日记 2024/9/6 13:33:41

树状数组记录

树状数组&#xff08;Fenwick Tree&#xff09;是一种用于维护数组前缀和的数据结构&#xff0c;支持高效的单点更新和区间查询操作。它的查询和更新时间复杂度为 O ( log ⁡ n ) O(\log n) O(logn)&#xff0c;适用于需要频繁更新和查询的场景。 树状数组的基本操作 单点更…...

编程日记 2024/9/6 13:30:39

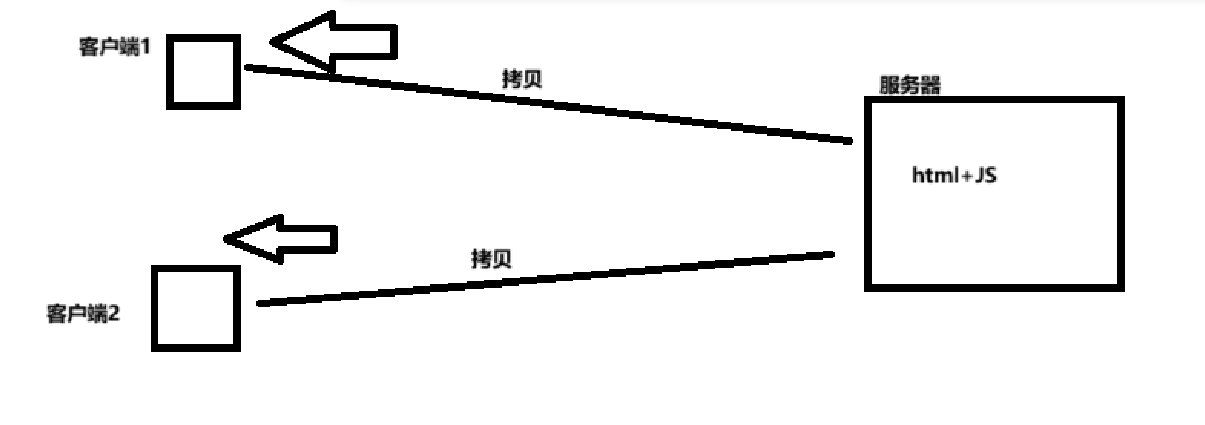
客户端时间和服务器时间的区别

客户端时间&#xff1a; 服务器向客户端拷贝一份前端内容&#xff0c;客户端通过JS获取时间&#xff0c;这样获取的是客户端时间 服务器时间&#xff1a; 服务器通过java代码获取的时间传输给客户端&#xff0c;这样获取的是服务器时间 当有些时候需要使用客户端时间&#xf…...

编程日记 2024/9/6 13:28:37

已入职华为！！关于我成功拿下华为大模型算法岗经验总结

方向:大模型算法工程师 整个面试持续了1小时10分钟&#xff0c;能够看出面试官是典型搞技术的&#xff0c;问的很专业又很细&#xff0c;全程感觉压力好大&#xff0c;面完后感觉丝丝凉意&#xff0c;不过幸好还是成功拿下了Offer 一面: 自我介绍 简历项目深度交流 1.项目的背…...

编程日记 2024/9/6 13:27:37

从安卓开发到AI产品经理——我的AI绘画之旅

大家好&#xff0c;我是一名有着多年安卓开发经验的程序员。在日复一日的编码生活中&#xff0c;我对AI行业产生了浓厚的兴趣。于是&#xff0c;我决定转行成为一名AI产品经理。在这个过程中&#xff0c;我通过学习AI绘画工具初步了解了AI行业&#xff0c;下面我将分享我的学习…...

编程日记 2024/9/6 13:26:36

代码随想录八股训练营第三十四天| C++

前言 一、vector和list的区别&#xff1f; 1.1.存储方式&#xff1a; 1.2.随机访问&#xff1a; 1.3.插入和删除操作&#xff1a; 1.4.内存使用&#xff1a; 1.5.容量和大小&#xff1a; 1.6.迭代器类型&#xff1a; 1.7.用途&#xff1a; 二、vector 底层原理和扩容过…...

编程日记 2024/9/6 13:25:34

《深入理解 Java 中的 this 关键字》

目录 一、this关键字的基本理解 二、this调用属性和方法 &#xff08;一&#xff09;一般情况 &#xff08;二&#xff09;特殊情况 三、this调用构造器 四、案例分析 &#xff08;一&#xff09;Account类 &#xff08;二&#xff09;Customer类 &#xff08;三&…...

编程日记 2024/9/6 13:24:34

python文件自动分类（5）

完成了文件自动分类的操作后&#xff0c;我们一起来复习下&#xff1a; 首先&#xff0c;获取文件夹中所有文件名称&#xff0c;用 os.path.join() 函数拼接出要移动到的目标地址。然后&#xff0c;使用 os.path.exists() 函数判断目标文件夹是否存在&#xff0c;不存在用 os.m…...

编程日记 2024/9/6 13:23:32

【Unity-Lua】音乐播放器循环滚动播放音乐名

前言&#xff1a;Unity中UI节点 图1 如上所示&#xff0c;一开始本来是打算用ScrollView做的&#xff0c;觉得直接计算对应的文本位置就行&#xff0c;所以没用ScrollRect来做&#xff0c;可以忽略Scroll&#xff0c;Viewport这些名字。如下图&#xff1a;需要在一个背景Image…...

编程日记 2024/9/6 13:22:31

宏碁扩展Swift系列，推出四款全新AI笔记本电脑

Acer正在扩展其Swift笔记本产品线&#xff0c;推出四款新型号&#xff0c;每款都内置了AI功能。这些笔记本提供诸如Microsoft Copilot、Acer用户感应技术、Windows Studio效应、PurifiedVoice 2.0和PurifiedView等功能。其他功能还包括Wi-Fi 7和Bluetooth 5.4连接。 我们先来看…...

编程日记 2024/9/6 13:21:30

科研绘图系列：R语言差异基因四分图（Quad plot）

文章目录 介绍加载R包导入数据数据预处理画图参考介绍 四分图（Quad plot）是一种数据可视化技术，通常用于展示四个变量之间的关系。它由四个子图组成，每个子图都显示两个变量之间的关系。四分图的布局通常是2x2的网格，每个格子代表一个变量对的散点图。 在四分图中，通常…...

编程日记 2024/9/6 13:18:26

文字或图案点选坐标点返回

最近看到这篇文章中讲到极验图片验证码破解方案 https://blog.geetest.com/article/65aaaa944edc5ec343ba9f52efef0cdc 其中核心解决步骤如下&#xff0c;作者还贴心的贴出了CNN代码&#xff0c;真是用心良极&#xff1a; step 3&#xff1a;批量下载存储验证图片&#xff0c;…...

编程日记 2024/9/6 13:17:26

硬盘数据恢复软件TOP4榜单出炉，选对方法竟然如此重要

这年头&#xff0c;信息多得不得了&#xff0c;数据对我们来说太重要了。但是&#xff0c;不管是咱们自己还是公司&#xff0c;都可能碰上丢数据的倒霉事&#xff0c;特别是不小心把硬盘里的东西删了。数据一丢&#xff0c;不光可能亏钱&#xff0c;工作和生活也可能受影响。好…...

编程日记 2024/9/6 13:16:25

给自己复盘用的随想录笔记-栈与队列

用栈实现队列 难在出去 232. 用栈实现队列 - 力扣&#xff08;LeetCode&#xff09; class MyQueue {private Stack<Integer> A;private Stack<Integer> B;public MyQueue() {Anew Stack<>();Bnew Stack<>();}public void push(int x) {A.push(x);}pu…...

编程日记 2024/9/6 13:15:23

8k长序列建模，蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂

蛋白质结合剂&#xff08;如抗体、抑制肽&#xff09;在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上&#xff0c;高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术&#xff0c;但这类方法普遍面临资源消耗巨大、研发周期冗长…...

编程新知 2026/1/25 13:18:12

什么是库存周转？如何用进销存系统提高库存周转率？

你可能听说过这样一句话&#xff1a; “利润不是赚出来的&#xff0c;是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业&#xff0c;很多企业看着销售不错&#xff0c;账上却没钱、利润也不见了&#xff0c;一翻库存才发现&#xff1a; 一堆卖不动的旧货…...

编程新知 2026/1/26 13:21:10

在四层代理中还原真实客户端ngx_stream_realip_module

一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡&#xff08;如 HAProxy、AWS NLB、阿里 SLB&#xff09;发起上游连接时&#xff0c;将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后&#xff0c;ngx_stream_realip_module 从中提取原始信息…...

编程新知 2026/1/4 5:02:00

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式

点一下关注吧&#xff01;&#xff01;&#xff01;非常感谢&#xff01;&#xff01;持续更新&#xff01;&#xff01;&#xff01; &#x1f680; AI篇持续更新中&#xff01;&#xff08;长期更新&#xff09; 目前2025年06月05日更新到&#xff1a; AI炼丹日志-28 - Aud…...

编程新知 2026/2/6 11:05:22

DBAPI如何优雅的获取单条数据

API如何优雅的获取单条数据 案例一 对于查询类API&#xff0c;查询的是单条数据&#xff0c;比如根据主键ID查询用户信息&#xff0c;sql如下&#xff1a; select id, name, age from user where id #{id}API默认返回的数据格式是多条的&#xff0c;如下&#xff1a; {&qu…...

编程新知 2026/2/2 22:06:13

Python ROS2【机器人中间件框架】 简介

销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

编程新知 2026/1/29 9:12:46

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强：基于微服务与容器化的解决方案

在大数据时代&#xff0c;海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构&#xff0c;在处理大规模数据抓取任务时展现出强大的能力。然而&#xff0c;随着业务规模的不断扩大和数据抓取需求的日益复杂&#xff0c;传统…...

编程新知 2026/2/4 19:29:38

6.9-QT模拟计算器

源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

编程新知 2026/2/6 5:43:28

基于江科大stm32屏幕驱动，实现OLED多级菜单（动画效果），结构体链表实现(独创源码)

引言 在嵌入式系统中&#xff0c;用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例&#xff0c;介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单&#xff0c;执行相应操作&#xff0c;并提供平滑的滚动动画效果。 本文设计了一个…...

编程新知 2026/2/6 5:58:36

Java多线程实现之Runnable接口深度解析

Java多线程实现之Runnable接口深度解析 一、Runnable接口概述1.1 接口定义1.2 与Thread类的关系1.3 使用Runnable接口的优势 二、Runnable接口的基本实现方式2.1 传统方式实现Runnable接口2.2 使用匿名内部类实现Runnable接口2.3 使用Lambda表达式实现Runnable接口 三、Runnabl…...

编程新知 2025/9/15 15:07:19