第L2周:机器学习-线性回归
- 🍨 本文为🔗365天深度学习训练营 中的学习记录博客
- 🍖 原作者:K同学啊
目标:
- 学习简单线性回归模型和多元线性回归模型
- 通过代码实现:通过鸢尾花花瓣长度预测花瓣宽度
具体实现:
(一)环境:
语言环境:Python 3.10
编 译 器: PyCharm
框 架:scikit-learn
(二)具体步骤:
造个数据集,内容格式如下:
导入库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
简单线性回归
# 加载数据
dataset = pd.read_csv('./studentscores.csv')
print(dataset)
# 取第一列Hours的值
X = dataset.iloc[:, :1].values
print(X)

# 取第二列Scores的值
Y = dataset.iloc[:, 1].values
print(Y)

很好奇,看看X,Y的形状:
print(X.shape)
print(Y.shape)

看来两者是一样的形状和大小 。继续:
# 切分一下数据集,75%用来训练,25%用来测试
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=1/4, random_state=0)
检验一下切分的成果:
print(X_train, X_train.shape)

print(Y_train, Y_train.shape)
print(X_test, X_test.shape)
print(Y_test, Y_test.shape)
做简单线性回归
# 简单线性回归
from sklearn.linear_model import LinearRegression regressor = LinearRegression()
regressor = regressor.fit(X_train, Y_train)# 预测一下结果
Y_pred = regressor.predict(X_test) print(Y_pred, Y_pred.shape)
这个预测结果和上面的Y_test比较一下,可以看到两者之间的差距以及相似性。我们进行可视化直观看看:
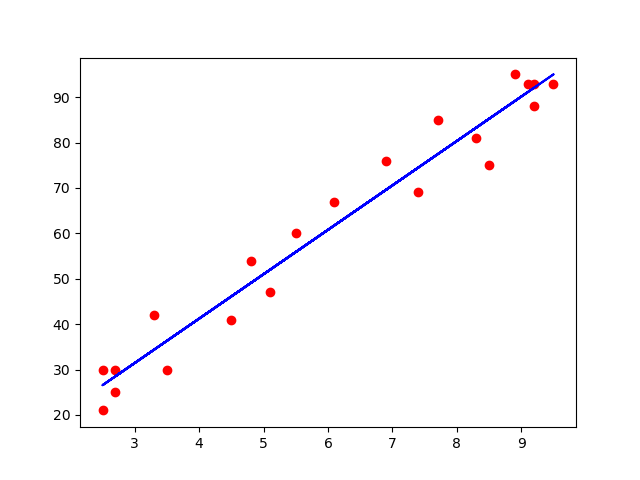
# 训练集可视化
plt.scatter(X_train, Y_train, color='red')
plt.plot(X_train, regressor.predict(X_train), color='blue')
plt.show()
**
# 测试集预测结果可视化
plt.scatter(X_test, Y_test, color='red')
plt.plot(X_test, regressor.predict(X_test), color='blue')
plt.show()
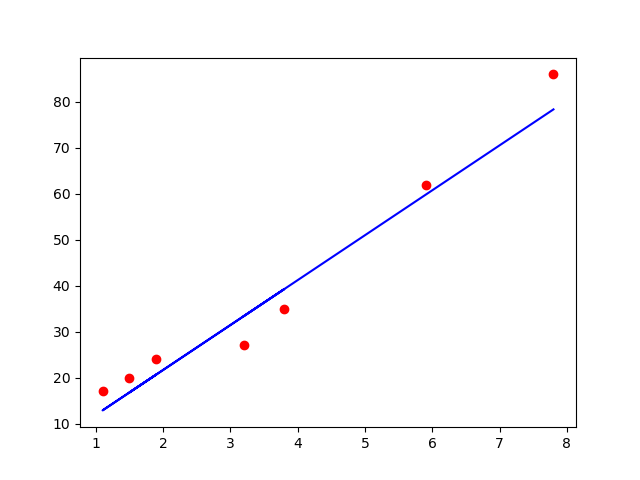
红点是实际分布,蓝色线是预测趋势线。两者是趋于一致的,预测的偏离并不大。
注:plt.scatter()绘制散点图,plt.plot()绘制折线图。
下面看看多元线性回归,通过鸢尾花花瓣长度预测花瓣宽度
- 导入数据集
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
names = ['花萼-length', '花萼-width', '花瓣-length', '花瓣-width', 'class']
dataset = pd.read_csv(url, names=names)
print(dataset)
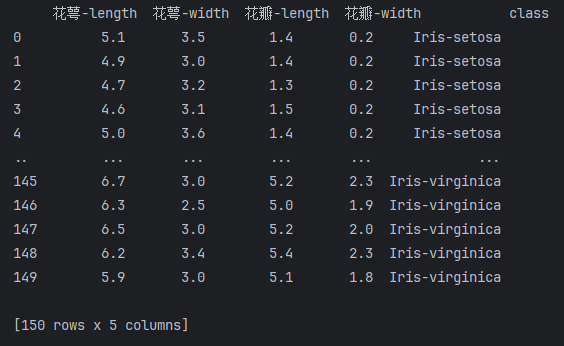
2. 分析一下数据
plt.plot(dataset['花萼-length'], dataset['花瓣-width'], 'x', label="marker='x'")
plt.plot(dataset['花萼-width'], dataset['花瓣-width'], 'o', label="marker='o'")
plt.plot(dataset['花瓣-length'], dataset['花瓣-width'], 'v', label="marker='v'")
plt.legend(numpoints=1)
plt.show()
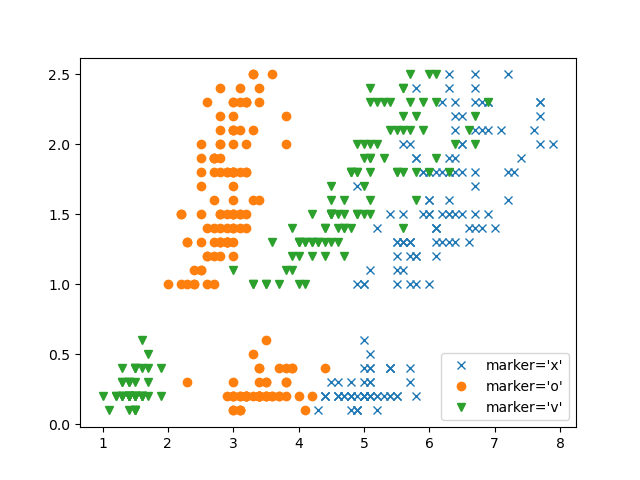
3. 取数据
# 取[花萼-width : 花瓣-length]
X = dataset.iloc[:, [1, 2]].values
print(X, X.shape)

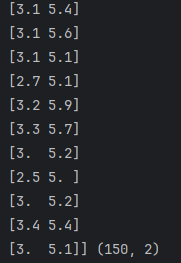
Y = dataset.iloc[:, 3].values # 取花瓣-width值
print(Y, Y.shape)
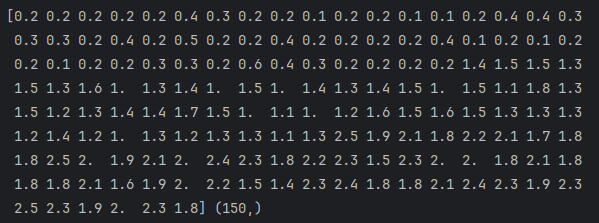
3. 将dataset切分成训练数据集和测试数据集
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)
- 训练多元线性回归模型
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, Y_train)
- 在测试集上预测结果
y_pred = regressor.predict(X_test)
print(y_pred)
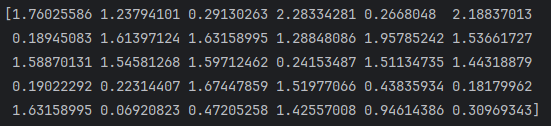
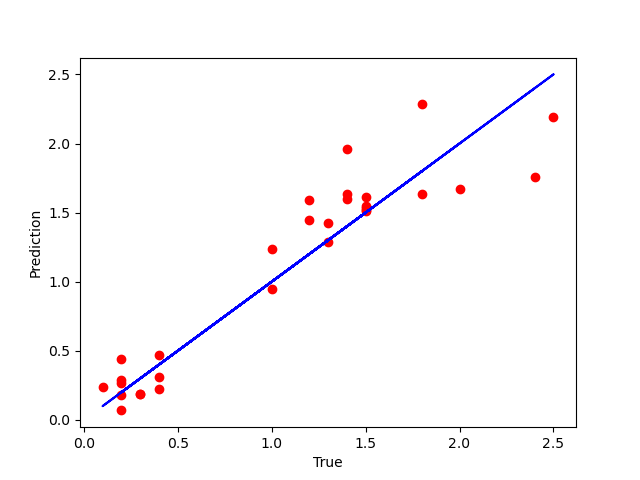
6. 把测试集预测结果可视化
plt.scatter(Y_test, y_pred, color='red')
plt.plot(Y_test, Y_test, color='blue') # 假设预测100%正确,那么走势是蓝线
plt.plot(Y_test)
plt.xlabel("True")
plt.ylabel("Prediction")
plt.show()
相关文章:

第L2周:机器学习-线性回归
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 目标: 学习简单线性回归模型和多元线性回归模型通过代码实现:通过鸢尾花花瓣长度预测花瓣宽度 具体实现: (一&…...

SpringMVC拦截器深度解析与实战
引言 Spring MVC作为Spring框架的核心模块之一,主要用于构建Web应用程序和RESTful服务。在Spring MVC中,拦截器(Interceptor)是一种强大的机制,它允许开发者在请求处理流程的特定点插入自定义代码,实现诸如…...

直线上最多的点数
优质博文:IT-BLOG-CN 题目 给你一个数组points,其中points[i] [xi, yi]表示X-Y平面上的一个点。求最多有多少个点在同一条直线上。 示例 1: 输入:points [[1,1],[2,2],[3,3]] 输出:3 示例 2: 输入&am…...

经济管理专业数据库介绍
本文介绍了四个经济管理专业数据库:国研网全文数据库、EPS数据平台、中经网、Emerald全文期刊库(管理学)。 一、国研网全文数据库 国研网是国务院发展研究中心主管、北京国研网信息有限公司承办的大型经济类专业网站。国研网教育版”是国研…...

【C++ Primer Plus习题】11.1
问题: 解答: main.cpp #include <iostream> #include <fstream> #include "Vector.h" #include <time.h> using namespace std; using namespace VECTOR;int main() {ofstream fout;fout.open("randwalk.txt");srand(time(0));double d…...

[数据库][oracle]ORACLE EXP/IMP的使用详解
导入/导出是ORACLE幸存的最古老的两个命令行工具,其实我从来不认为Exp/Imp是一种好的备份方式,正确的说法是Exp/Imp只能是一个好的转储工具,特别是在小型数据库的转储,表空间的迁移,表的抽取,检测逻辑和物理…...

中国各银行流动性比例数据(2000-2022年)
介绍中国银行业2000年至2022年间的流动性比例数据,涵盖500多家银行,包括城市商业银行、城镇银行、大型商业银行、股份制银行、民营银行、农村合作银行、农村商业银行、农村信用社等。这些数据对于理解中国银行业的流动性状况至关重要,有助于投…...

MACOS安装配置前端开发环境
官网下载安装Mac版本的谷歌浏览器以及VS code代码编辑器,还有在App Store中直接安装Xcode(里面自带git); node.js版本管理器nvm的下载安装如下: 参考B站:https://www.bilibili.com/video/BV1M54y1N7fx/?sp…...
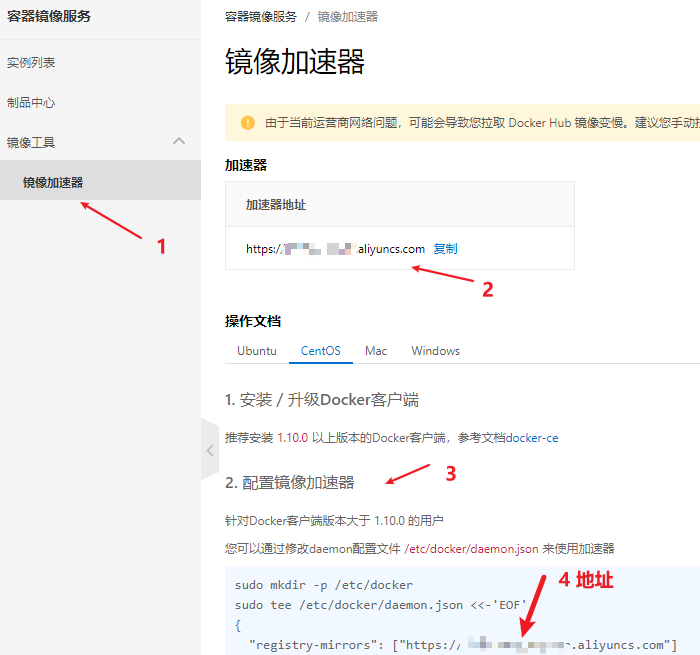
Docker 配置国内镜像源
由于 GFW 的原因,在下载镜像的时候,经常会出现下载失败的情况,此时就可以使用国内的镜像源。 什么是镜像源:简单来说就是某个组织(学校、公司、甚至是个人)先通过某种手段将国外的镜像下载下来,…...

AI模块在人工智能中扮演着什么样的角色
AI模块在人工智能(AI)中扮演着核心和关键的角色。它们是构成AI系统的基础单元,负责实现AI系统的各种智能功能。以下是AI模块在人工智能中扮演的具体角色: 功能实现的核心:AI模块集成了实现特定智能功能所需的算法、数据…...
VM Workstation虚拟机AlmaLinux 9.4操作系统安装(桌面版安装详细教程)(宝塔面板的安装),填补CentOS终止支持维护的空白
目录 AlmaLinux介绍 AlmaLinux操作系统的安装 1、下载镜像文件 2、新建虚拟机 (1)点击创建新的虚拟机 (2)打开虚拟机向导后,选择“自定义”安装,然后点击“下一步” (3)选择虚…...

【学习笔记】卫星通信NTN 3GPP标准化进展分析(三)- 3GPP Release17 内容
一、引言: 本文来自3GPP Joern Krause, 3GPP MCC (May 14,2024) Non-Terrestrial Networks (NTN) (3gpp.org) 本文总结了NTN标准化进程以及后续的研究计划,是学习NTN协议的入门。 【学习笔记】卫星通信NTN 3GPP标准化进展分析(一ÿ…...

【SQL】常见语句合集
SQL常见语句合集 一. 新建表1.1 语句1.2 结果 二. 新增数据2.1 语句2.2 结果 三. 新增字段列3.1 语句3.2 结果3.3 扩展 四. 更新指定数据4.1 语句4.2 结果 五. 更新指定列5.1 语句(长度) 六. 删除字段列6.1 语句 七. 删除指定数据7.1 语句 八. 查询 一. …...
)
Cozer必备!一站式解锁扣子全网最全插件集锦(三)
俗话说,工欲善其事必先利其器! 用过Coze的朋友都知道,插件在Coze里的重要性。插件库就相当于武器库,一个好的插件,就相当于一件趁手的兵器,可以让你事半功倍! 程哥精心整理了Coze最常用和好用…...

1-2宿主环境
什么是宿主环境 指的是程序运行所必须的依赖环境。Android系统和ios系统是两个不同的宿主环境,安卓版的app是不能在ios系统上运行的。 小程序的宿主环境 🍕🍕🍕 -手机微信是小程序的宿主环境 通信的主体 🍔&…...

Java进阶13讲__第九讲
Stream流 1. 案例初体验 package cn.hdc.oop9.stream.using;import java.util.LinkedList; import java.util.List; import java.util.stream.Collectors; import java.util.stream.Stream;public class t1 {public static void main(String[] args) {LinkedList<String&g…...

上海市计算机学会竞赛平台2024年8月月赛丙组等差数列的素性
题目描述 给定三个整数 nn,aa 与 dd,表示一个项数为 nn 的等差数列,首项为 aa,公差为 dd。 请统计,从这个等差数列中有多少数字是素数 输入格式 三个整数: nn,aa 与 dd 输出格式 单个整数…...

VR虚拟展厅的应用场景有哪些?
虚拟展厅作为一种利用虚拟现实技术构建的三维展示空间,其应用场景广泛且多样。视创云展为企业虚拟展厅搭建提供技术支持。以下是一些主要的应用场景: 1. 博物馆和艺术展览 文物保护与展示: 在博物馆中,为了保护珍贵的文物和艺术…...

Go 语言版本管理——Goenv
Go 语言版本管理——Goenv 命令安装 goenv安装和切换 Go 版本 goenv 是一个专门管理 Go 语言版本的工具。 命令 安装 goenv github-goenv git clone https://github.com/go-nv/goenv.git ~/.goenv echo export GOENV_ROOT"$HOME/.goenv" >> ~/.bash_profile…...
和径向渐变的区别)
C#中的各种画刷, PathGradientBrush、线性渐变(LinearGradientBrush)和径向渐变的区别
在C#中,画刷(Brush)是用来填充图形(如形状或文本)内部区域的对象。在.NET框架中,画刷是System.Drawing命名空间的一部分,通常用于GDI绘图操作。以下是一些常用的画刷类型: SolidBru…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...
