关于位运算的巧妙性:小乖,你真的明白吗?
一.位运算的概念
什么是位运算?
程序中的所有数在计算机内存中都是以二进制的形式储存的。位运算就是直接对整数在内存中的二进制位进行操作。
位运算就是直接操作二进制数,那么有哪些种类的位运算呢?
常见的运算符有与(&)、或(|)、异或(^)、取反(~)、左移(<<)、右移(>>是带符号右移 >>>无符号右移动)。下面来细看看每一种位运算的规则。
&操作符:运算规则:将两个数字的二进制位进行按位与操作,即当两个数字的某位二进制数中同时为1结果才为1,否则是0 0&0=0, 0&1=0, 1&1=1
例子:

位运算 | (或)
规则:二进制对应位两两进行逻辑或运算(对应位中有一 个为1则为1) 即0|0=0,0|1=1,1|1=1

3.位运算 ^ (异或)
规则:二进制对应位两两进行逻辑XOR (异或) 的运算(当对应位的值不同时为 1, 否则为 0)即0^0=0, 0^1=1, 1^1=0

4.
按位取反~
规则:二进制的0变成1,1变成0。
5.
左移运算<<:左移后右边位补 0
右移运算>>:右移后左边位补原最左位值(可能是0,可能是1)
右移运算>>>:右移后左边位补 0
关于位运算的规则,我们再进行详细的讲述:关于左移,无论对于正数还是负数,结果都是在原来数值的基础上进行乘2操作,但是对于右移符号,这其中就有说法了:>>>,对于无符号右移:它的运算规则是将原有数字右移,在左边补0,也就是说,如果原有的数字是负数,通过无符号右移会变成正数,对于正数则是简单的除2的效果,对于>>右移符号,则是无论对于正数还是负数,达到的效果都是除2
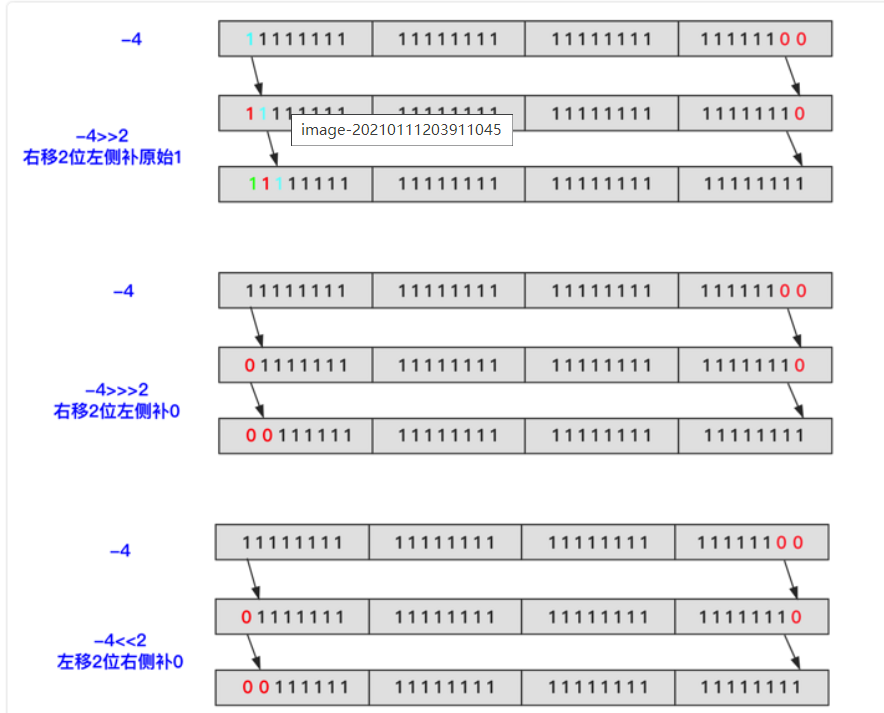
二.关于位运算的常见题目
交换两个数
利用位运算将数个数值进行交换
a=a^b;//a=a^b
b=a^b;//b=(a^b)^b=a^0=a
a=a^b;//a=(a^b)^(a^b^b)=0^b=0判断奇偶数
给定一个数值,判断这个数字是奇数还是偶数
if(n & 1 == 1){// n 是个奇数。
}不用加减乘除做加法
牛客链接:https://www.nowcoder.com/practice/e7e0d226f1e84ba7ab8b28efc6e1aebc?tpId=8&&tqId=11065&rp=1&ru=/activity/oj&qru=/ta/cracking-the-coding-interview/question-ranking
实现思路:关于实现加法运算而不使用加减乘除运算,我们则可以选择调用相关的位运算进行求解
①按位异或(^):可以实现无进位的加法运算
比如: 1 ^ 1 = 0 ---> 1 + 1 = 0 (当前位值为0,进一位)
1 ^ 0 = 1 ---> 1 + 0 = 1 (当前位值为1)
0 ^ 0 = 0 ---> 0 + 0 = 0 (当前位值为0
②按位与(&)然后左移一位:能够表示进位情况:
比如: 1 & 1 = 1 ---> 1 + 1 = 0 (当前位的值进一位)
1 & 0 = 0 ---> 1 + 0 = 1 (当前位的值不进位)
0 & 0 = 0 ---> 0 + 0 = 0 (当前位的值不进位)
③
两个数相加:对应二进制位相加的结果 + 进位的结果
比如:3 + 2 --> 0011 + 0010 --> 0011 ^ 0010 + ((0011 & 0010) << 1)
---> (0011 ^ 0010) ^ ((0011 & 0010) << 1), 当进位之后的结果为0时,相加结束
public int addAB(int A, int B) {
// write code here
if(B==0){
return A;
}
int sum=0;
int carray=0;
while(B!=0){
sum=A^B;
carray=(A&B)<<1;
A=sum;
B=carray;
}
return A;
}求出现一次的数字①
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
实现思路:
根据异或运算的特性,我们能够理解的是:任何数字异或自身,结果都是0,所以对于所有成对出现的数字而言,我们将其全部异或一遍,其结果是0,再将唯一出现的数字再次异或,最后的结果也就是那个唯一出现的数字。
我们给出code:
class Solution {public int singleNumber(int[] nums) {int value=0;for(int i=0;i<nums.length;i++){value^=nums[i];}return value;}
}求出现一次的数字②
一个整型数组 nums 里除两个数字之外,其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。
LeetCode链接:https://leetcode.cn/problems/shu-zu-zhong-shu-zi-chu-xian-de-ci-shu-lcof/solution/jian-zhi-offer-56-i-shu-zu-zhong-shu-zi-tykom/
与①有所不同的是,这次题目的给出的条件是有两个不同的数字,让我们分别找出这两个数字,既然仍然是出现多组出现两次的数字,那么我们的实现大思路仍然保持不变,就是通过不断异或来排除出现两次的数字,那么这时候便引出了问题的关键,异或之后剩下的结果是两个数字异或之后的结果,那么我们如何在结果中将这两个数字分别拿出来呢?这里我们选择的策略是区分两个数字中不同的一位,具体实现思路如下:首先将所有数字进行异或,将最后生成的结果与m(m=1)进行异或,目的是找出异或结果中为1的一位(因为两个不同的数字必然有一位不同,异或结果是1),我们利用这个辨识特点,分别对数组进行分组异或,最后的两个数字就是异或的结果,具体code如下:
class Solution {public int[] singleNumbers(int[] nums) {//因为相同的数字异或为0,任何数字与0异或结果是其本身。//所以遍历异或整个数组最后得到的结果就是两个只出现一次的数字异或的结果:即 z = x ^ yint z = 0; for(int i : nums) z ^= i;//我们根据异或的性质可以知道:z中至少有一位是1,否则x与y就是相等的。//我们通过一个辅助变量m来保存z中哪一位为1.(可能有多个位都为1,我们找到最低位的1即可)。//举个例子:z = 10 ^ 2 = 1010 ^ 0010 = 1000,第四位为1.//我们将m初始化为1,如果(z & m)的结果等于0说明z的最低为是0//我们每次将m左移一位然后跟z做与操作,直到结果不为0.//此时m应该等于1000,同z一样,第四位为1.int m = 1;while((z & m) == 0) m <<= 1;//我们遍历数组,将每个数跟m进行与操作,结果为0的作为一组,结果不为0的作为一组//例如对于数组:[1,2,10,4,1,4,3,3],我们把每个数字跟1000做与操作,可以分为下面两组://nums1存放结果为0的: [1, 2, 4, 1, 4, 3, 3]//nums2存放结果不为0的: [10] (碰巧nums2中只有一个10,如果原数组中的数字再大一些就不会这样了)//此时我们发现问题已经退化为数组中有一个数字只出现了一次//分别对nums1和nums2遍历异或就能得到我们预期的x和yint x = 0, y = 0;for(int i : nums) {//这里我们是通过if...else将nums分为了两组,一边遍历一遍异或。//跟我们创建俩数组nums1和nums2原理是一样的。if((i & m) == 0) x ^= i;else y ^= i;}return new int[]{x, y};}
}实现思路:
6.求出现一次的数字③
在一个数组 nums 中除一个数字只出现一次之外,其他数字都出现了三次。请找出那个只出现一次的数字。
LeetCode链接:https://leetcode.cn/problems/shu-zu-zhong-shu-zi-chu-xian-de-ci-shu-ii-lcof/
实现思路:相对于出现两次的数字,能够利用异或的规律解决问题,出现三次的数字显得毫无规律可言,那么我们又该如何解决出现三次的数字问题呢?我们可以观察其每一位数字的规律:对于每一位数字而言,既然是出现三次,那么则可以对数组中的每一位数字的32个二进制位进行遍历,记录每一位的结果,至于最后返回的数字,我们可以通过res(res=0)和数组中的每一位进行%3然后进行或操作,然后将res左移,让二进制中的每一位回到原来的位置即可,code如下:
class Solution {public int singleNumber(int[] nums) {int[] counts = new int[32];for(int num : nums) {for(int j = 0; j < 32; j++) {counts[j] += num & 1;num >>>= 1;}}int res = 0, m = 3;for(int i = 0; i < 32; i++) {res <<= 1;res |= counts[31 - i] % m;}return res;}
}
7.n皇后问题的位运算优化
notes:需要注意的是,利用位运算解决n皇后问题的暴力递归问题只是对效率问题进行常数级别的优化:
limit:是位数限制,对于行列数为N的棋盘,limit的限制是:对于前N个二进制位数均为1,对于N行列的棋盘而言,前N个二进制位代表棋盘的每一行(第一个二进制位代表第一行,第二个代表第二行........)
①col:对于每次摆放个皇后,就将这个二进制位置变为1,表示这个二进制位不能摆放皇后了
②leftLim:左斜线限制,如果leftLim为1,代表对于当前行来说,这个位置不能摆放皇后了。
③RightLim:右斜线限制,如果RightLim为1,同样对于当前行来说,这个位置不能摆放皇后了。
④limit==col:代表col前N个二进制位都是1,表示N个皇后都已经摆放好了,游戏结束,退出递归
⑤limit&(~(col|leftLim|rightLim)):pos是在每一行中能选择的列

⑥ mostRight=pos&(~pos+1):取出最右边的一位
⑦ pos-=mostRight:将最右边的位置从可选择的位数中去除,使当前行不能放置皇后
⑧while(pos!=0) 循环当前行中能选择的位置
⑨res+= process2(limit,col|mostRight,(leftLim|mostRight)<<1, (rightLim|mostRight)>>>1):循环下一层
code如下:
public static int process2(int limit,int col,int leftLim,int rightLim){//递归出口if(limit==col){return 1;}//计算能放的位置:int pos= limit&(~(col|leftLim|rightLim));int mostRight=0;int res=0;//检验是否能递归while(pos!=0){//找最右的位置mostRight=pos&(~pos+1);pos-=mostRight;res+= process2(limit,col|mostRight,(leftLim|mostRight)<<1, (rightLim|mostRight)>>>1);}return res;相关文章:

关于位运算的巧妙性:小乖,你真的明白吗?
一.位运算的概念什么是位运算?程序中的所有数在计算机内存中都是以二进制的形式储存的。位运算就是直接对整数在内存中的二进制位进行操作。位运算就是直接操作二进制数,那么有哪些种类的位运算呢?常见的运算符有与(&)、或(|)、异或(^)、…...

【Android车载系列】第5章 AOSP开发环境配置
1 硬件支持 建议空闲内存16G以上,同时硬盘400G以上 内存不够可以使用 Linux 的交换分区2 VMware Workstation安装 https://download3.vmware.com/software/wkst/file/VMware-workstation-full-16.1.1-17801498.exe2.1 Ubuntu镜像 http://mirrors.aliyun.com/ubun…...
个人时间管理网站—Git项目管理
🌟所属专栏:献给榕榕🐔作者简介:rchjr——五带信管菜只因一枚😮前言:该专栏系为女友准备的,里面会不定时发一些讨好她的技术作品,感兴趣的小伙伴可以关注一下~👉文章简介…...

2023最新ChatGPT整理的40道Java高级面试题
2023 年最火的就是 ChatGPT 了,很多同事使用他完成一些代码上的智能提示,也有人使用它发了财《「用ChatGPT年入百万!」各博主发布生财之道,网友:答辩搬运工》、《“躺着就能赚大钱”?ChatGPT火了,有人早就动起坏脑筋》等。 最近我也使用 ChatGPT 写技术文章了,比如:《…...
单机分布式一体化是什么?真的是数据库的未来吗,OceanBase或将开启新的里程碑
一. 数据 我们先说说数据这个东西,这段时间的ChatGPT在全世界的爆火说明了一件事,数据是有用的,并且大量的数据如果有一个合适的LLM大规模语言模型训练之后,可以很高程度的完成很多意想不到的事情。 我们大多数的时候的注意力只…...

100天精通Python丨基础知识篇 —— 03、Python基础知识扫盲(第一个Python程序,13个小知识点)
文章目录🐜 1、Python 初体验Pycharm 第一个程序交互式编程第一个程序🐞 2、Python 引号🐔 3、Python 注释🦅 4、Python 保留字符🐯 5、Python 行和缩进🐨 6、Python 空行🐹 7、Python 输出&…...
springboot逍遥大药房管理系统
084-springboot逍遥大药房管理系统演示录像开发语言:Java 框架:springboot JDK版本:JDK1.8 服务器:tomcat7 数据库:mysql 5.7 数据库工具:Navicat11 开发软件:eclipse/myeclipse/idea Maven包&a…...

ZYNQ中的GPIO与AXI GPIO
GPIO GPIO—一种外设,对器件进行观测和控制MIO—将来自PS外设和静态存储器接口的访问多路复用到PS引脚上处理器控制外设的方法—通过一组寄存器包括状态寄存器和控制寄存器,这些寄存器都是有地址的,通过这些寄存器的读写进行外设的控制sessi…...

接口导入功能
1.接口api export function import(param) { return fetch({ url: XXX.import, method: POST, headers: { Content-Type: multipart/form-data; }, data: param }) } 2.页面vue 和 js逻辑 <el-button :loading"disable&qu…...

网络安全知识点总结 期末总结
1、信息安全从总体上可以分成5个层次,密码技术 是信息安全中研究的关键点。 2、握手协议 用于客户机与服务器建立起安全连接之前交换一系列信息的安全信道。 3、仅设立防火墙系统,而没有 安全策略 ,防火墙就形同虚设。 4、应用代理防火墙 …...
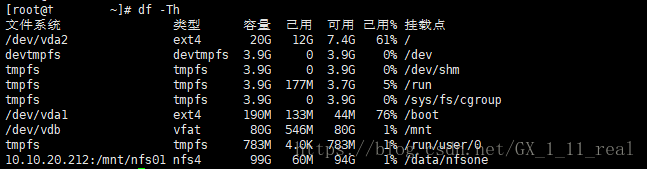
linux挂载远程目录
服务端操作 # 1、安装NFS程序 yum -y install nfs* rpcbind,在centos6以前自带的yum源中为portmap。 使用yum安装nfs时会下载依赖,因此只要下载nfs即可,无需再下载rpcbind. # 2、查看是否安装了nfs与rpcbind rpm -qa | grep nfs rpm -qa | grep rpc…...

ChatGPT—初识
ChatGPT初识 由于ChatGPT 注册相关的文章被平台限制了,所以有注册相关的问题可以私聊,或者可以代注册 Chat GPT是一款基于GPT模型的对话型AI模型,能够模拟真实的对话风格和行为方式,让人与AI的交互变得更加自然顺畅。下面将从Chat…...

【ArcGIS Pro二次开发】(18):地理处理工具类【Geoprocessing】补遗
ArcGIS Pro SDK 3.0中的Geoprocessing类是用于执行地理处理工具的核心类。地理处理工具是用于执行空间分析、数据转换、数据管理等任务的工具集,包括常见的空间分析工具、栅格处理工具、矢量处理工具、地图制图工具等。 之前有简单记录了下Geoprocessing工具的用法…...
国产芯片方案——红外测温体温计方案
红外测温体温计采用了热电堆式,利用塞贝克效应,将收集到的红外线光信号转化为电信号,再经过放大等处理,按内部的算法校正后再显示屏幕上输出具体温度值,能快速准确地测量人体体温。红外测温体温计广泛应用于医疗卫生、…...
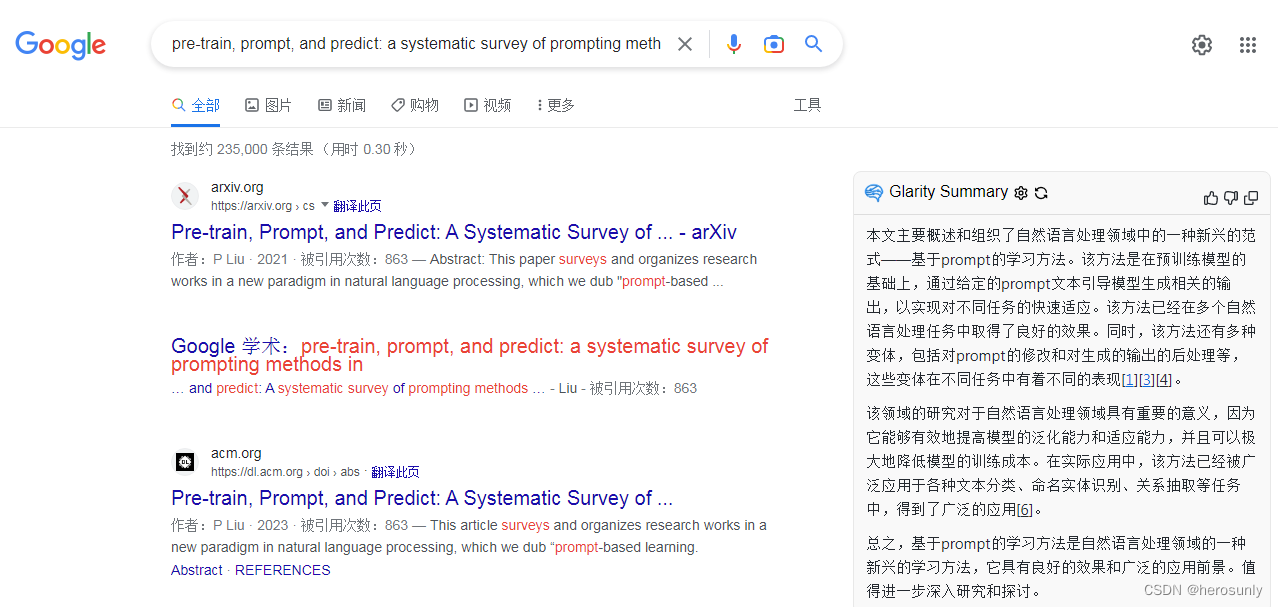
详解ChatGPT的免费总结插件Glarity
大家好,我是herosunly。985院校硕士毕业,现担任算法研究员一职,热衷于机器学习算法研究与应用。曾获得阿里云天池比赛第一名,科大讯飞比赛第三名,CCF比赛第四名。拥有多项发明专利。对机器学习和深度学习拥有自己独到的见解。曾经辅导过若干个非计算机专业的学生进入到算法…...

RK3588平台开发系列讲解(NPU篇)NPU调试方法
平台内核版本安卓版本RK3588Linux 5.10Android 12文章目录 一、日志等级二、NPU 支持查询设置项沉淀、分享、成长,让自己和他人都能有所收获!😄 📢本篇我们一起来看一下NPU的调试方法。 一、日志等级 NPU 的运行库会根据开发板上的系统环境变量输出一些日志信息或者生成…...

基于微信小程序+爬虫制作一个表情包小程序
跟朋友聊天斗图失败气急败坏的我选择直接制作一个爬虫表情包小程序,从源头解决问题,从此再也不用担心在斗图中落入下风 精彩专栏持续更新↓↓↓ 微信小程序实战开发专栏 一、API1.1 项目创建1.2 图片爬虫帮助类1.3 测试窗体1.4 接口封装二、小程序2.1 项…...
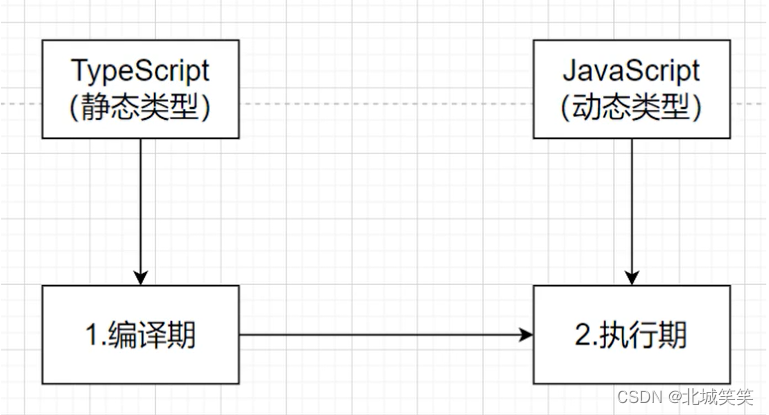
TS常用数据类型(TypeScript常用数据类型,ts常用数据类型和js常用数据类型的区别)
简述:TS全称TypeScript,是一门弱类型的语言,可以理解为是 JavaScript 的扩展语法,因此我们可以在 ts 中继续写js代码,且不会报错,而且TypeScript 又叫做静态的JavaScript,可称为静态类型语言&am…...

关于Numpy的特殊符号@和矩阵运算
符号之谜 在Numpy中,看到了符号,但是无论是google搜索或者baidu搜索,由于符号是一个特殊字符,所以很难检索到答案。 其实很简单,他就是Numpy库中的一个操作符,在numpy库的说明中,落在numpy.mat…...

动态版通讯录——“C”
各位CSDN的uu们你们好呀,今天,小雅兰的内容是动态版通讯录啦,其实之前,我就已经写过静态版的通讯录了,只是存在着一些问题,具体细节可以详细看看我的静态版通讯录,好了,话不多说&…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

HTML版英语学习系统
HTML版英语学习系统 这是一个完全免费、无需安装、功能完整的英语学习工具,使用HTML CSS JavaScript实现。 功能 文本朗读练习 - 输入英文文章,系统朗读帮助练习听力和发音,适合跟读练习,模仿学习;实时词典查询 - 双…...

解密鸿蒙系统的隐私护城河:从权限动态管控到生物数据加密的全链路防护
摘要 本文以健康管理应用为例,展示鸿蒙系统如何通过细粒度权限控制、动态权限授予、数据隔离和加密存储四大核心机制,实现复杂场景下的用户隐私保护。我们将通过完整的权限请求流程和敏感数据处理代码,演示鸿蒙系统如何平衡功能需求与隐私安…...
