Python实现混合蛙跳算法
博客目录
-
引言
- 什么是混合蛙跳算法(Shuffled Frog Leaping Algorithm, SFLA)?
- 混合蛙跳算法的应用场景
- 为什么使用混合蛙跳算法?
-
混合蛙跳算法的原理
- 混合蛙跳算法的基本概念
- 蛙群分组与局部搜索
- 全局混洗与更新
- 混合蛙跳算法的流程
-
混合蛙跳算法的实现步骤
- 初始化蛙群
- 局部搜索
- 全局混洗
- 寻找全局最优解
-
Python实现混合蛙跳算法
- 面向对象思想设计
- 代码实现
- 示例与解释
-
混合蛙跳算法应用实例:函数优化问题
- 场景描述
- 算法实现
- 结果分析与可视化
-
混合蛙跳算法的优缺点
- 优点分析
- 潜在的缺点与局限性
- 如何改进混合蛙跳算法
-
总结
- 混合蛙跳算法在优化问题中的作用
- 何时使用混合蛙跳算法
- 其他常用的优化算法
1. 引言
什么是混合蛙跳算法(SFLA)?
混合蛙跳算法(Shuffled Frog Leaping Algorithm, SFLA)是一种基于群体智能的优化算法,由Eusuff和Lansey于2003年提出。SFLA模拟了青蛙在不同区域间跳跃和在池塘内局部搜索食物的行为,结合了遗传算法(GA)和粒子群优化(PSO)的一些思想,尤其擅长解决连续和离散的优化问题。
混合蛙跳算法的应用场景
混合蛙跳算法适用于以下场景:
- 函数优化:适用于多维空间的连续函数优化。
- 路径规划:在交通网络和机器人导航中的路径优化问题。
- 数据聚类:在数据挖掘中的聚类问题。
- 资源分配:在调度和物流中进行资源优化配置。
为什么使用混合蛙跳算法?
SFLA结合了局部搜索和全局搜索的优势,能够避免陷入局部最优解并快速收敛到全局最优解。其简单性、效率和良好的性能使其成为处理复杂优化问题的有力工具。
2. 混合蛙跳算法的原理
混合蛙跳算法的基本概念
SFLA是一种元启发式优化算法,通过模拟青蛙在“池塘”中的行为来寻找问题的最优解。蛙群分为多个子群(称为蛙塘),每个蛙塘执行局部搜索,之后通过混合操作将子群组合在一起,以加速全局收敛。
蛙群分组与局部搜索
- 初始化蛙群:在问题空间中随机生成一组解(青蛙),每只青蛙的位置代表一个可能的解。
- 分组成蛙塘:蛙群被划分为多个子群(蛙塘),每个蛙塘独立进行局部搜索。
- 局部搜索:在每个蛙塘中,青蛙通过模仿最优青蛙(局部最优解)来调整自己的位置,从而不断优化自身。
全局混洗与更新
- 全局混洗:每次局部搜索后,重新混洗所有蛙塘中的青蛙,以促进青蛙在全局范围内的搜索。
- 迭代更新:经过若干次局部搜索和全局混洗,蛙群最终会收敛到全局最优解。
混合蛙跳算法的流程
- 初始化蛙群和参数:设置蛙群大小、蛙塘数量、最大迭代次数等参数。
- 分组蛙塘并进行局部搜索:在每个蛙塘中,青蛙通过局部搜索更新位置。
- 全局混洗并更新:将所有青蛙重新混合以加强全局探索。
- 判断终止条件:如果达到最大迭代次数或满足收敛条件,输出最优解;否则,继续搜索。
3. 混合蛙跳算法的实现步骤
以下是实现SFLA算法的主要步骤:
初始化蛙群
随机生成一组青蛙,每只青蛙的位置代表一个解。
局部搜索
在每个蛙塘内,青蛙向局部最优解移动。
全局混洗
将所有蛙塘中的青蛙重新混合,以增强全局探索能力。
寻找全局最优解
每次迭代更新全局最优解,直到满足终止条件。
4. Python实现混合蛙跳算法
下面是一个基于面向对象思想的Python实现,用于演示SFLA算法的实现过程。
面向对象思想设计
在面向对象的设计中,我们可以将SFLA算法的组件划分为以下类:
Frog类:表示单只青蛙,包含位置、适应度值等属性。FrogPond类:表示蛙塘,包含局部搜索和混洗操作。SFLA类:表示混合蛙跳算法,包含蛙群初始化、局部搜索、全局混洗等方法。
代码实现
import numpy as npclass Frog:def __init__(self, dimensions, bounds):self.position = np.random.uniform(bounds[0], bounds[1], dimensions)self.fitness = float('inf')self.dimensions = dimensionsself.bounds = boundsdef evaluate(self, fitness_function):"""计算青蛙的适应度值。"""self.fitness = fitness_function(self.position)def move_towards(self, target_position, step_size):"""向目标位置移动一定的步长。"""direction = target_position - self.positionself.position += step_size * directionself.position = np.clip(self.position, self.bounds[0], self.bounds[1])class FrogPond:def __init__(self, frogs, step_size):self.frogs = frogsself.step_size = step_sizedef local_search(self, fitness_function):"""局部搜索:在蛙塘内调整青蛙的位置以逼近局部最优解。"""best_frog = min(self.frogs, key=lambda frog: frog.fitness)worst_frog = max(self.frogs, key=lambda frog: frog.fitness)worst_frog.move_towards(best_frog.position, self.step_size)worst_frog.evaluate(fitness_function)class SFLA:def __init__(self, num_frogs, dimensions, bounds, num_ponds, max_iter, fitness_func, step_size):self.num_frogs = num_frogsself.dimensions = dimensionsself.bounds = boundsself.num_ponds = num_pondsself.max_iter = max_iterself.fitness_func = fitness_funcself.step_size = step_sizeself.frogs = [Frog(dimensions, bounds) for _ in range(num_frogs)]self.ponds = []self.global_best_position = Noneself.global_best_fitness = float('inf')def initialize_ponds(self):"""初始化蛙塘,将青蛙分组到不同的蛙塘中。"""np.random.shuffle(self.frogs)frogs_per_pond = len(self.frogs) // self.num_pondsself.ponds = [FrogPond(self.frogs[i * frogs_per_pond: (i + 1) * frogs_per_pond], self.step_size)for i in range(self.num_ponds)]def shuffle_frogs(self):"""全局混洗:将所有青蛙重新混合并分组。"""np.random.shuffle(self.frogs)self.initialize_ponds()def optimize(self):"""主优化过程,包含局部搜索和全局混洗。"""for frog in self.frogs:frog.evaluate(self.fitness_func)for iteration in range(self.max_iter):self.initialize_ponds()# 局部搜索for pond in self.ponds:pond.local_search(self.fitness_func)# 更新全局最优解for frog in self.frogs:if frog.fitness < self.global_best_fitness:self.global_best_fitness = frog.fitnessself.global_best_position = frog.position# 全局混洗self.shuffle_frogs()return self.global_best_position, self.global_best_fitness
示例与解释
在上述代码中:
Frog类表示单个青蛙及其行为,如评估适应度和移动。FrogPond类管理一个蛙塘内的所有青蛙,执行局部搜索。SFLA类是混合蛙跳算法的核心,实现了蛙群的初始化、局部搜索和全局混洗的逻辑。
5. 混合蛙跳算法应用实例:函数优化问题
场景描述
我们使用以下简单的二次函数作为目标优化问题:
f ( x , y ) = x 2 + y 2 f(x, y) = x^2 + y^2 f(x,y)=x2+y2
算法实现
使用上述SFLA类,我们可以定义适应度函数并运行优化过程。
# 定义适应度函数
def fitness_function(position):x, y = positionreturn x**2 + y**2# 参数设置
dimensions = 2
bounds = [-10, 10]
num_frogs = 50
num_ponds = 5
max_iter = 100
step_size = 0.5# 初始化SFLA算法
sfla = SFLA(num_frogs, dimensions, bounds, num_ponds, max_iter, fitness_function, step_size)# 运行优化
best_position, best_fitness = sfla.optimize()print(f"最佳位置: {best_position}, 最佳适应度值: {best_fitness}")
结果分析与可视化
通过上述实现,我们可以观察混合蛙跳算法逐渐逼近函数的最小值。
import matplotlib.pyplot as plt# 可视化优化结果
positions = np.array([frog.position for frog in sfla.frogs])
plt.scatter(positions[:, 0], positions[:, 1], label="青蛙的位置")
plt.scatter(best_position[0], best_position[1], color='red', label="最佳位置")
plt.legend()
plt.show()
6. 混合蛙跳算法的优缺点
优点分析
- 全局与局部搜索的结合:能够有效避免陷入局部最优解。
- 自适应搜索:结合遗传算法和粒子群优化的特点,具有较强的灵活性和适应性。
- 参数设置较为简单:相对于其他优化算法,SFLA的参数设置较为简单,且不敏感。
潜在的缺点与局限性
- 复杂度:在大型问题中,蛙群和蛙塘的管理可能会导致复杂度增加。
- 收敛速度:在某些情况下,收敛速度可能不如专门的优化算法。
如何改进混合蛙跳算法
- 多样性增强:引入更多的随机因素以增加群体的多样性。
- 改进局部搜索策略:结合其他局部优化算法,提升局部搜索的效率。
7. 总结
混合蛙跳算法(SFLA)是一种强大的优化算法,能够在全局搜索和局部搜索之间取得平衡,广泛应用于各种优化问题中。通过Python面向对象的实现,我们可以看到SFLA算法的结构清晰、易于实现,并能够有效解决实际问题。希望读者通过本文能够更好地理解SFLA算法,并在实际项目中应用这一算法。
相关文章:

Python实现混合蛙跳算法
博客目录 引言 什么是混合蛙跳算法(Shuffled Frog Leaping Algorithm, SFLA)?混合蛙跳算法的应用场景为什么使用混合蛙跳算法? 混合蛙跳算法的原理 混合蛙跳算法的基本概念蛙群分组与局部搜索全局混洗与更新混合蛙跳算法的流程 …...

印度再现超级大片,豪华阵容加顶级特效
最近,印度影坛再次掀起了风潮,一部名为《毗湿奴降临》的神话大片强势登陆各大影院,上映首周票房就飙升至105亿卢比,成功占据了票房榜首的位置。之后,这部电影也在北美上映,海外市场的表现同样不俗ÿ…...

Git使用经验总结6-删除远端历史记录
删除远端的历史记录但是不影响最新的仓库内容是笔者一直想实现的功能,有两个很不错的用处: 有的历史提交不慎包含了比较敏感的信息,提交的时候没注意,过了一段时间才发现。这个时候已经有了很多新的历史提交,无法再回…...
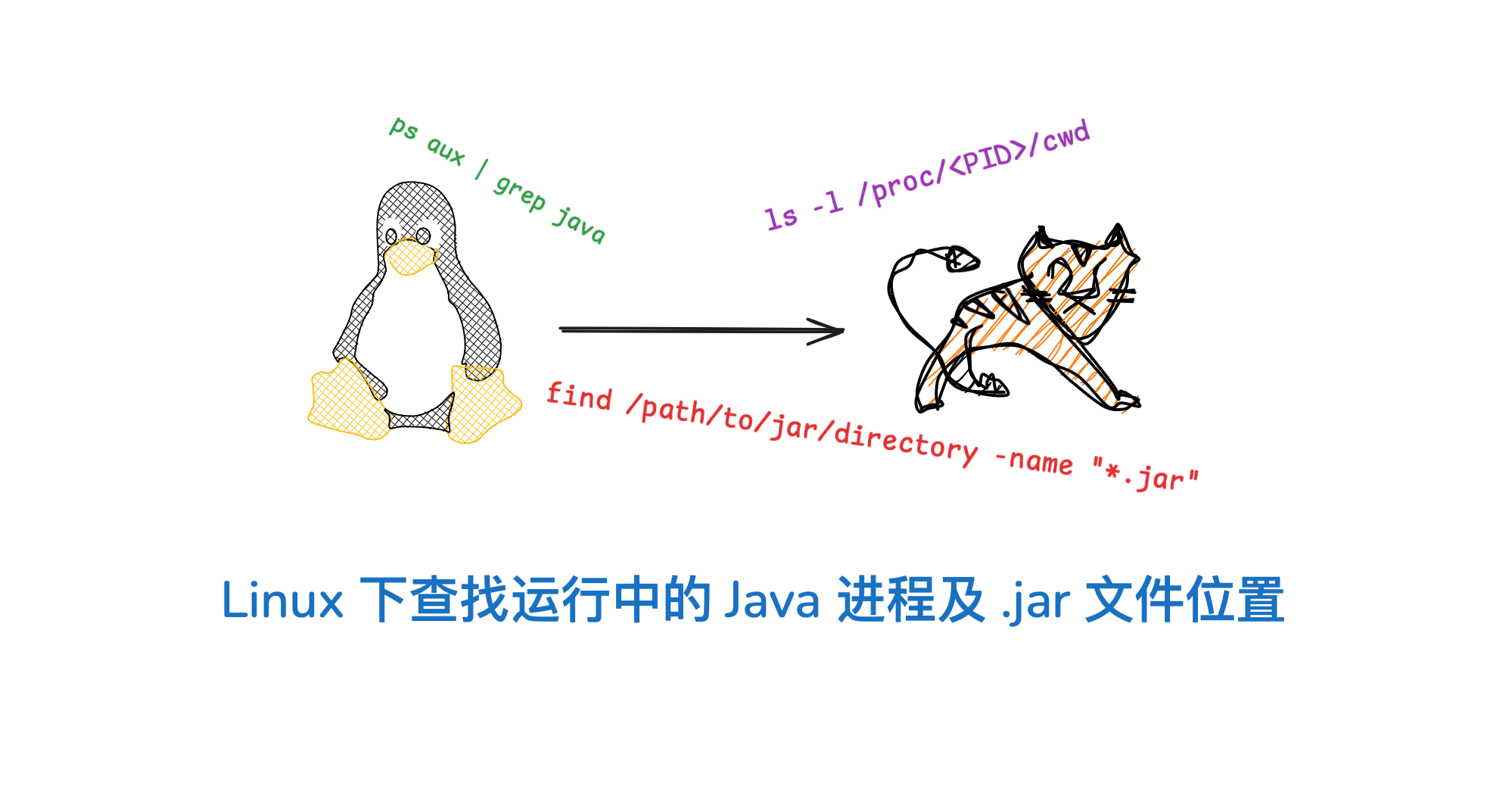
Linux 下查找运行中的 Java 进程及 .jar 文件位置
在 Linux 环境中,有时我们需要查找正在运行的 Java 进程以及它们对应的 .jar 文件位置。本文将介绍如何使用命令行工具来实现这一目标。 前言 在 Linux 系统中,我们经常需要监控正在运行的应用程序,特别是在出现问题时,了解应用程…...

Openwrt 安装 AX210 无线网卡
安装 TTYD 我安装的是官方原版的 Openwrt,首先需要安装 YYTD 来从网页控制 Openwrt。 安装驱动 参考这个链接,跟着做。 iwlwifi-firmware-ax210 不要直接拷贝粘贴,CSDN 复制文字最后面有网站添加的信息。 lspci opkg update opkg instal…...

在VitePress中进行页面链接:最佳实践与实例
在使用VitePress构建静态网站时,页面之间的链接是必不可少的。本文将介绍如何在VitePress中正确链接页面,包括内部页面和外部非VitePress页面的链接方法,并通过实例代码进行详细解释。 一、链接VitePress内部页面 在VitePress中,…...

Qt/C++百度地图/高德地图/天地图/腾讯地图/谷歌地图/加载绘图工具栏
一、前言说明 在地图中提供一个绘图工具栏,可以便捷的在地图上添加各种覆盖物,比如折线、多边形、矩形、圆形等,然后可以获取这些覆盖物的路径以及中心点等属性。这里有几个小插曲,比如百度地图gl版本默认不提供这个功能…...

Vue2 与 Vue3 的区别有哪些
Vue 2 和 Vue 3 在许多方面都有显著的区别,包括性能、API 设计、功能特性等。以下是它们主要的区别: 1. 响应式系统 Vue 2: 基于 Object.defineProperty: Vue 2 使用 Object.defineProperty 来实现响应式数据。这种方法在处理对象属性时有一定的局限性…...

加锁造成的线程优先级反转
优先级反转(Priority Inversion),也称优先级翻转,一般是在优先级不同的多线程环境中发生。在桌面操作系统中,线程的优先级不是太重要,因此较少见优先级反转的现象。但是,优先级反转是实时操作系统(RTOS)中一个常见的问题,特别是在采用优先级调度算法的系统中。这个问…...

【日常记录-Java】SpringBoot中使用无返回值的异步方法
Author:赵志乾 Date:2024-09-05 Declaration:All Right Reserved!!! 1. 简介 在SpringBoot中,使用Async注解可以很方便地标记一个方法为异步执行。好处是调用者无需等待这些方法完成便可继续执…...
【深度学习】多层感知机的从零开始实现与简洁实现
可以说,到现在我们才真正接触到深度网络。最简单的深度网络称为多层感知机。 多层感知机由多层神经元组成,每一层与它的上一层相连,从中接收输入;同时每一层也与它的下一层相连,影响当前层的神经元。 和以前相同&…...

4、Django Admin对自定义的计算字段进行排序
通常,Django会为模型属性字段,自动添加排序功能。当你添加计算字段时,Django不知道如何执行order_by,因此它不会在该字段上添加排序功能。 如果要在计算字段上添加排序,则必须告诉Django需要排序的内容。你可以通过在…...

rsync搭建全网备份
rsync搭建全网备份 1. 总体概述1.1 目标1.2 简易指导图1.3 涉及工具或命令1.4 环境 2. 实施2.1 配置备份服务器2.2 备份文件准备2.3 整合命令2.4 扩展功能 1. 总体概述 1.1 目标 本次搭建目标: 每天定时把服务器数据备份到备份服务器备份完成后进行校验把过期数据…...

网络安全售前入门09安全服务——安全加固服务
目录 1.服务概述 2.流程及工具 2.1服务流程 2.2服务工具 3.服务内容 4.服务方式 5.风险规避措施 6.服务输出 1.服务概述 安全加固服务是参照风险评估、等保测评、安全检查等工作的结果,基于科学的安全思维方式、长期的安全…...

【Android】GreenDao数据库的使用方式
需求 使用GreenDao数据库进行数据的存储。 介绍 GreenDao 是一个轻量级的对象关系映射(ORM)库,用于简化 Android 应用中的数据库操作。它提供了以下主要功能: 简化数据库操作:通过注解定义实体类,Green…...
)
搜索算法之线性搜索详细解读(附带Java代码解读)
1. 基本概念 线性搜索(Linear Search),也称为顺序搜索,是一种在列表中查找特定元素的算法。它从列表的第一个元素开始,逐个检查每个元素,直到找到目标元素或检查完所有元素。 2. 工作原理 线性搜索的操作…...

Quartz.Net_依赖注入
简述 有时会遇到需要在IJob实现类中依赖注入其他类或接口的情况,但Quartz的默认JobFactory并不能识别具有有参构造函数的IJob实现类,也就无法进行依赖注入 需要被依赖注入的类: public class TestClass {public TestClass(Type jobType, s…...

【系统架构设计师-2011年】综合知识-答案及详解
更多内容请见: 备考系统架构设计师-核心总结索引 文章目录 【第1题】【第2~4题】【第5~7题】【第8题】【第9题】【第10题】【第11题】【第12题】【第13题】【第14题】【第15题】【第16题】【第17题】【第18~19题】【第20~21题】【第22题】【第23题】【第24题】【第25题】【第2…...

World of Warcraft [CLASSIC][80][Grandel]Sapphire Hive Drone
Sapphire Hive Drone 蓝玉虫巢雄蜂 蓝玉虫巢巨峰 索拉查盆地 实用性不强,好看是好看,模型很大,无奈栏位太少...

Unity 对接 Android 第三方广告,App 切换到后台后,再次打开时,第三方广告被销毁导致无法触发回调逻辑的问题
该问题是由发行进行游戏测试时遇到并反馈的。大致情况如下: 1. 当触发了插屏广告后,在关闭广告前将 App 切换到后台,之后再次打开 App,此时插屏广告消失,并切游戏卡死。 2. 当触发激励视频广告后,在广告展…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...
