python数值误差
最近在用fenics框架跑有限元代码,其中有一个部分是把在矩阵里定义的初始值,赋值到有限元空间里,这就涉及到了初始矩阵和有限元空间坐标的转化,部分代码如下
for i in range(len(dof_coordinates)):# x, y = dof_coordinates[i]#原本的区间是0到physical_length的,根据num_grids_per_axis长度进行缩放.# ix, iy = min(int(x / physical_length * (num_grids_per_axis - 1)), num_grids_per_axis - 1), min(int(y / physical_length * (num_grids_per_axis - 1)), num_grids_per_axis - 1)ix, iy = min(int(x * (num_grids_per_axis - 1) / physical_length), num_grids_per_axis - 1), min(int(y * (num_grids_per_axis - 1) / physical_length), num_grids_per_axis - 1)这里有一点需要注意:
x要先和num_grids_per_axis相乘,然后再除以physical_length。先除再乘的话,数学逻辑上一样,但是如果一个很小的数,除以一个很大的数,会有舍入误差。所以先乘再除。
相关文章:

python数值误差
最近在用fenics框架跑有限元代码,其中有一个部分是把在矩阵里定义的初始值,赋值到有限元空间里,这就涉及到了初始矩阵和有限元空间坐标的转化,部分代码如下 for i in range(len(dof_coordinates)):# x, y dof_coordinates[i…...

基于FPGA的OV5640摄像头图像采集
1.OV5640简介 OV5640是OV(OmniVision)公司推出的一款CMOS图像传感器,实际感光阵列为:2592 x 1944(即500w像素),该传感器内部集成了图像出炉的电路,包括自动曝光控制(AEC…...

CDN ❀ Http协议标准缓存字段梳理
文章目录 1. 背景介绍2. 测试环境搭建3. 缓存字段3.1 Expires3.2 Cache-Control3.3 协商缓存 1. 背景介绍 Http协议标准有RFC定义好的请求和响应头部字段用于进行缓存设置,本文主要进行介绍缓存功能相关的头部字段及其使用方法。在使用CDN功能是,协议标…...

浅谈NODE的NPM命令和合约测试开发工具HARDHAT
$ npm install yarn -g # 将模块yarn全局安装 $ npm install moduleName # 安装模块到项目目录下 默认跟加参数 --save 一样 会在package文件的dependencies节点写入依赖。 $ npm install -g moduleName # -g 的意思是将模块安装到全局,具体安装到磁盘哪个位置&…...
)
k8s-pod 实战六 (如何在不同的部署环境中调整startupprobe的参数?)
在不同的部署环境中(如开发、测试、生产环境),你可能希望对 startupProbe 的参数进行调整,以适应不同的需求和条件。以下是几种常见的方法和实践: 方法一:使用 Kustomize 1. 目录结构 假设你的项目目录结构如下: my-app/ ├── base/ │ └── deployment.yaml …...

和服务端系统的通信
首先web网站 前端浏览器 和 后端系统 是通过HTTP协议进行通信的 同步请求&异步请求: 同步请求:可以从浏览器中直接获取的(HTML/CSS/JS这样的静态文件资源),这种获取请求的http称为同步请求 异步请求:js代码需要到服…...

python 实现perfect square完全平方数算法
python 实现perfect square完全平方数算法介绍 完全平方数(Perfect Square)是一个整数,它可以表示为某个整数的平方。例如,1,4,9,16,25,… 都是完全平方数,因为 1 1 2 , 4 2 2 , 9 3 2 11^2,42^2,93^2 112,422,93…...

【漏洞复现】某客圈子社区小程序审计(0day)
0x00 前言 █ 纸上得来终觉浅,绝知此事要躬行 █ Fofa:"/static/index/js/jweixin-1.2.0.js"该程序使用ThinkPHP 6.0.12作为框架,所以直接审计控制器即可.其Thinkphp版本较高,SQL注入不太可能,所以直接寻找其他洞. 0x01 前台任意文件读取+SSRF 在 /app/api/c…...

信息安全数学基础(1)整除的概念
前言 在信息安全数学基础中,整除是一个基础且重要的概念。它涉及整数之间的特定关系,对于理解数论、密码学等领域至关重要。以下是对整除概念的详细阐述: 一、定义 设a, b是任意两个整数,其中b ≠ 0。如果存在一个整数q࿰…...

SearchGPT与谷歌:早期分析及用户反馈
光年AI系统,作为先进AI技术的成果,推出了一个AI驱动搜素引擎的原型,类似于SearchGPT。 该发布引起了广泛的关注,并引发了关于其是否有能力与Google竞争的讨论。 然而,早期的研究和用户反馈表明,虽然Searc…...

VUE饿了么UPload组件自定义上传
代码: 1.视图: <el-dialog :title"dialogTitle" width"30%" :visible.sync"dialogFormVisible" :destroy-on-close"true"><el-form ref"fileForm" class"items-align" ><e…...

2.1概率统计的世界
欢迎来到概率统计的世界!在量化交易中,概率统计是至关重要的工具。通过理解概率,我们可以用数学的方法来描述市场行为,预测未来走势,并制定交易策略。让我们一起从基础概念开始,逐步深入,揭开概…...

SpringBoot使用QQ邮箱发送邮件
1.开启POP3/IMAP/SMTP/Exchange/CardDAV/CalDAV服务 设置 -> 账号 -> POP3/IMAP/SMTP/Exchange/CardDAV/CalDAV服务 获取授权码 SpringBoot依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter&l…...

使用 OpenCV 和 NumPy 进行图像处理:HSV 范围筛选实现PS抠图效果
使用 OpenCV 和 NumPy 进行图像处理:HSV 范围筛选实现PS抠图效果 在计算机视觉和图像处理领域,OpenCV 是一个非常强大的库,能够帮助我们执行各种图像操作。在这篇博客中,我们将通过一个简单的示例演示如何使用 OpenCV 和 NumPy 来…...

IIS中间件
中间件 中间件是一类软件,为应用程序、服务和组件提供一个通用的服务层。 主要功能 通信:提供通信框架,帮助不同系统与应用之间进行数据交换和通信 事务管理、资源管理 安全服务:提供认证、授权、加密等安全策略 数据访问&a…...

BMP280气压传感器详解(STM32)
目录 一、介绍 二、传感器原理 1.原理图 2.引脚描述 3.传感器数据获取流程 三、程序设计 main.c文件 bmp280.h文件 bmp280.c文件 四、实验效果 五、资料获取 项目分享 一、介绍 BMP280是一款基于博世公司APSM工艺的小封装低功耗数字复合传感器,它可以测…...
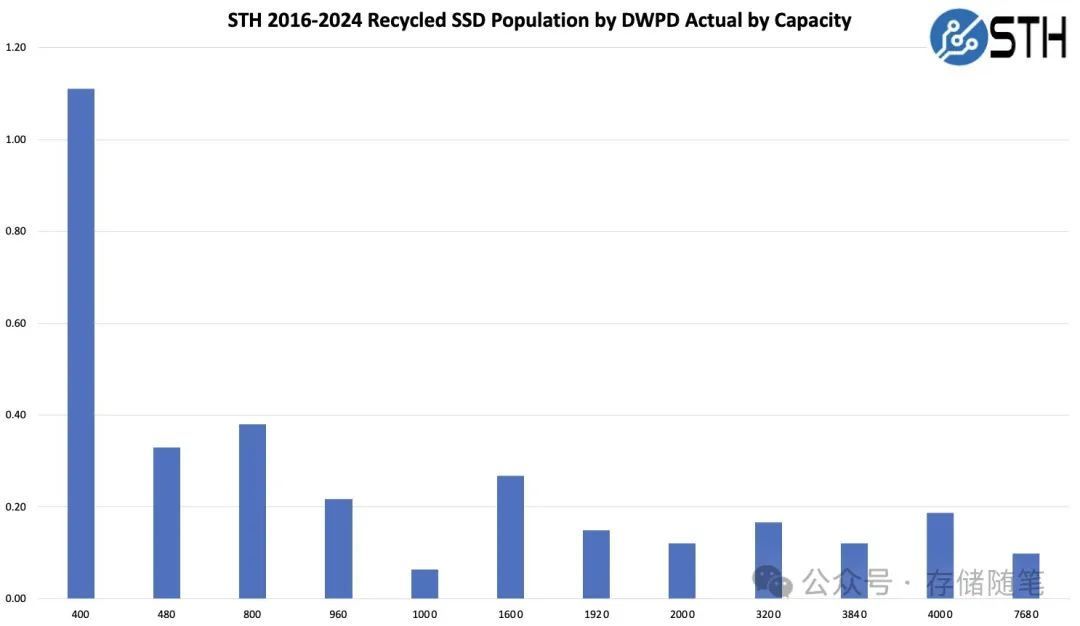
DWPD指标:为何不再适用于大容量SSD?
固态硬盘(Solid State Drives, SSD)作为计算机行业中最具革命性的技术之一,凭借其更快的读写速度、增强的耐用性和能效,已经成为大多数用户的首选存储方案。然而,如同任何其他技术一样,SSD也面临自身的挑战…...

路由器的固定ip地址是啥意思?固定ip地址有什么好处
在当今数字化时代,路由器作为连接互联网的重要设备,扮演着举足轻重的角色。其中,路由器的固定IP地址是一个常被提及但可能让人困惑的概念。下面跟着虎观代理小二一起将深入探讨路由器的固定IP地址的含义,揭示其背后…...

Java——踩坑Arrays.asList()
坑1:不能直接使用 Arrsys.asList() 来转换基本类型数据 public static void test1(){// 1、不能直接使用asList来转换基本类型数组int[] arr {1, 2, 3};List list Arrays.asList(arr);System.out.printf("list:%s size:%s class:%s", list, list.size(…...

前缀列表(ip-prefix)配置
一. 实验简介 本来前缀列表是要和访问控制列表放在一起讲的,但是这里单拎出来是为了更详细的讲解两者的区别 1.前缀列表针对IP比访问控制更加灵活。 2.前缀列表在后面被引用时是无法对数据包进行过滤的 实验拓扑 二. 实验目的 R4路由器中只引入子网LoopBack的…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
