对极约束及其性质 —— 公式详细推导
Title: 对极约束及其性质 —— 公式详细推导
文章目录
- 前言
- 1. 对极约束 (Epipolar Constraint)
- 2. 坐标转换 (Coordinate Transformations)
- 3. 像素坐标 (Pixel Coordinates)
- 4. 像素坐标转换 (Transformations of Pixel Coordinates)
- 5. 本质矩阵 (Essential Matrix)
- 6. 线坐标 (Coordinates of a Line)
- 7. 对极线 (Epipolar Lines)
- 8. 对极线的线坐标 (Coordinates of Epipolar Lines)
- 9. 本质矩阵的零空间 (Null Space of a Essential Matrix)
- 10. 本质矩阵的奇异值 (Singular Values of a Essential Matrix)
- 总结
- 参考文献
前言
参考学习资料 [1] (Carlo Tomasi, Epipolar Geometry and the Essential Matrix) 过程中, 对其坐标系描述存在疑问, 尝试自己推导了一下, 也补充了一些其他性质的推导.
形成了这篇博文, 以备忘.
1. 对极约束 (Epipolar Constraint)
对极几何就是描述两个相机之间的对极约束的几何[1], 如 Fig. 1 所示.

相机 a 其小孔成像 (中心投影) 的光心是 O a O_a Oa, 焦距是 f f f. 相机获得图像 I a I_a Ia, 图像中有像素点 P a {\rm{P}}_a Pa. 沿着射线 O a P ‾ \overline{O_aP} OaP 进行反向投影, 可知像素点 P a {\rm P}_a Pa 对应的物理世界中的场景点 P \rm P P 在投影线上.
另一相机 b 与相机 a 具有相同的相机内参 (可能就是同一相机的不同位姿), 两者之间的相互位姿关系是 { t , R } \{t, R\} {t,R}. 同一场景点 P \rm P P 也会在相机 b 的图像 I b I_b Ib 上成像为像素点 P b {\rm P}_b Pb.
因为从相机 a 视角还原的像素点 P a {\rm P}_a Pa 对应的物理世界场景点可能是 P \rm P P、 P ′ {\rm P'} P′ 或 P ′ ′ {\rm P''} P′′ 等, 只要在射线 O a P a ‾ \overline{O_a P_a} OaPa 上都可能是. 而这些可能的场景点 P \rm P P、 P ′ {\rm P'} P′ 或 P ′ ′ {\rm P''} P′′ 在相机 b 上作投影成像可能获得的像素点却是 P b {\rm P}_b Pb、 P b ′ {\rm P}_b' Pb′ 或 P b ′ ′ {\rm P}_b'' Pb′′ 这些不同位置的像素点.
因为像素点 P a {\rm P}_a Pa 和这些可能的像素点 P b {\rm P}_b Pb、 P b ′ {\rm P}_b' Pb′ 或 P b ′ ′ {\rm P}_b'' Pb′′ 都是对同一物理世界场景点 P \rm P P 的投影成像, 那么他们之间成在什么样的关系? 如何预测第二个相机上对应像素点位置? 这些就是对极约束要关注的.
2. 坐标转换 (Coordinate Transformations)
基于小孔成像模型的相机遵循中心射影原理, 射影中心在相机光心. 以相机光心作为坐标原点建立坐标系, Z 轴指向场景, X 轴向右, Y 轴向下.
有了相机坐标系后, 首先要面对同一场景点在两个相机坐标系中的坐标转换问题[2], 如 Fig. 2 所示.

相机坐标系 {a} 和 {b} 原点不重合并且姿态也不同.
a t b ^at_b atb 表示坐标系 {b} 的原点在坐标系 {a} 中的位置, a R b {^aR}_b aRb 表示坐标系 {b} 相对于坐标系 {a} 的姿态.
相反地, b t a ^bt_a bta 表示坐标系 {a} 的原点在坐标系 {b} 中的位置, b R a {^bR}_a bRa 表示坐标系 {a} 相对于坐标系 {b} 的姿态.
为方便理解可以构造过渡坐标系 {b’}, 在坐标系 {a} 中平移 a t b ^at_b atb 得到坐标系 {b’}, 在坐标系 {b’} 中旋转 b ′ R b ^{b'}R_b b′Rb 得到坐标系 {b}.
坐标系 {b’} 和 {b} 的原点重合, 故平移矩阵 a t b = a t b ′ ^at_b = {^at_{b'}} atb=atb′.
坐标系 {a} 和 {b’} 的姿态相同, 故旋转矩阵 b ′ R b = a R b ^{b'}R_b = {^aR}_b b′Rb=aRb.
空间中一点 P, 相对于坐标系 {a} 的坐标为 a p ^ap ap, 而同一点 P 相对于坐标系 {b} 的坐标为 b p ^bp bp.
根据刚体坐标变换关系可以得到
a p = b ′ R b b p + a t b ′ ⇒ a p = a R b b p + a t b ⇒ b p = a R b T ( a p − a t b ) ⇒ b p = b R a a p − b R a a t b (2-1) \begin{aligned} {^{a}p} &= {^{b'}R}_b {{^b}p}+{{^a}t_{b'}}\\ \Rightarrow \quad {^{a}p} &= {^{a}R}_b {{^b}p}+{{^a}t_b}\\ \Rightarrow \quad {^{b}p} &= {^{a}R}_b^{\rm{T}}\left({{^a}p}-{{^a}t_b}\right)\\ \Rightarrow \quad {^{b}p} &= {^{b}R}_a{{^a}p}- {^{b}R}_a {{^a}t_b} \end{aligned} \tag{2-1} ap⇒ap⇒bp⇒bp=b′Rbbp+atb′=aRbbp+atb=aRbT(ap−atb)=bRaap−bRaatb(2-1)
另外, 因为坐标系 {a} 和坐标系 {b’} 姿态相同, 故有
b ′ t a = − a t b ′ (2-2) {^{b'}}t_a = - {^at_{b'}} \tag{2-2} b′ta=−atb′(2-2)
已知坐标系 {b’} 中向量 b ′ t a {^{b'}}t_a b′ta, 下面需要将其转换为坐标系 {b} 中描述 b t a {^bt_a} bta. 也就是同一向量, 只是描述该向量的参考坐标系改变.
类比刚体坐标变换关系式 (2-1) 中第二行得到
b ′ t a = b ′ R b b t a + b ′ t b ⏟ = 0 ⇒ − a t b ′ = b ′ R b b t a ⇒ − a t b = a R b b t a ⇒ b t a = − a R b T a t b ⇒ b t a = − b R a a t b (2-3) {^{b'}}t_a ={^{b'}}R_b {^bt_a} + \underset{=0}{\underbrace{{^{b'}}t_b}}\\ \Rightarrow \qquad - {^at_{b'}} = {^{b'}}R_b {^bt_a}\\ \Rightarrow \qquad - {^at_{b}} = {^{a}}R_b {^bt_a}\\ \Rightarrow \qquad {^bt_a} = - {^{a}}R_b^{\rm T} {^at_{b}}\\ \Rightarrow \qquad {^bt_a} = - {^{b}}R_a {^at_{b}} \tag{2-3} b′ta=b′Rbbta+=0 b′tb⇒−atb′=b′Rbbta⇒−atb=aRbbta⇒bta=−aRbTatb⇒bta=−bRaatb(2-3)
结合式 (2-1) 和式 (2-3) 可得
b p = b R a a p + b t a (2-4) ^{b}p = {^{b}R}_a{{^a}p} + {^bt_a} \tag{2-4} bp=bRaap+bta(2-4)
为了简化书写, 定义
R ≜ b R a = a R b T t ≜ b t a = − b R a a t b (2-5) \begin{aligned} R & \triangleq {^{b}R}_a = {^{a}R}_b^{\rm{T}}\\ t & \triangleq {^bt_a} = - {^{b}R}_a {{^a}t_b} \end{aligned}\tag{2-5} Rt≜bRa=aRbT≜bta=−bRaatb(2-5)
则式 (2-4) 简写为
b p = R a p + t (2-6) ^{b}p = R \,{{^a}p}+{t} \tag{2-6} bp=Rap+t(2-6)
因为习惯上都是由 a p ^ap ap 而计算得到 b p ^bp bp, 故而写成式 (2-6) 形式.
3. 像素坐标 (Pixel Coordinates)
场景空间中一点 P 向相机 a 投影得到的像素点 P a \rm{P_a} Pa, 在二维成像平面 I a I_a Ia 上的坐标为
P a = [ x a y a ] (3-1) P_a = \begin{bmatrix}x_a \\ y_a \end{bmatrix} \tag{3-1} Pa=[xaya](3-1)
因为对极几何需要在三维空间中推导, 把该像素点 P a {\rm P}_a Pa 看作是一个实体点, 其在相机坐标系 {a} 中的三维坐标为
a p a = [ x a y a f ] (3-2) ^ap_a = \begin{bmatrix}x_a\\ y_a \\ f\end{bmatrix} \tag{3-2} apa= xayaf (3-2)
其中 f f f 为焦距 ( f ≠ 0 f \neq 0 f=0).
同理, 场景空间中一点 P 向相机 b 投影得到的像素点 P b {\rm P}_b Pb, 在二维成像平面 I b I_b Ib 上的坐标为
P b = [ x b y b ] (3-3) P_b = \begin{bmatrix}x_b \\ y_b \end{bmatrix} \tag{3-3} Pb=[xbyb](3-3)
把该像素点 P b {\rm P}_b Pb 看作是一个实体点, 其在相机坐标系 {b} 中的三维坐标为
b p b = [ x b y b f ] (3-4) ^bp_b = \begin{bmatrix}x_b\\ y_b \\ f\end{bmatrix} \tag{3-4} bpb= xbybf (3-4)
由射影关系可以知道, 坐标值 x a , y a , x b , y b x_{a},y_{a}, x_{b}, y_{b} xa,ya,xb,yb 受到 f f f 的正比例影响, 故而像素点在各自相机坐标系内的三维坐标其实也是齐次坐标.
4. 像素坐标转换 (Transformations of Pixel Coordinates)
在对极约束中投影线 O a P ‾ \overline{O_a P} OaP、投影线 O b P ‾ \overline{O_bP} ObP 和基线 O a O b ‾ \overline{O_a O_b} OaOb 共面. 则可知
向量 O a P a → \overrightarrow{O_a P_a} OaPa、向量 O a P b → \overrightarrow{O_a P_b} OaPb、向量 O a O b → \overrightarrow{O_a O_b} OaOb 共面;
向量 O b P b → \overrightarrow{O_b P_b} ObPb、向量 O b P a → \overrightarrow{O_b P_a} ObPa、向量 O b O a → \overrightarrow{O_b O_a} ObOa 共面.
进一步, 可知
( O a O b → × O a P a → ) ⊥ O a P b → (\overrightarrow{O_a O_b} \times \overrightarrow{O_a P_a}) \, \bot \, \overrightarrow{O_a P_b} (OaOb×OaPa)⊥OaPb 以及 ( O b O a → × O b P a → ) ⊥ O b P b → (\overrightarrow{O_b O_a} \times \overrightarrow{O_b P_a}) \, \bot \, \overrightarrow{O_b P_b} (ObOa×ObPa)⊥ObPb.
以上向量需要借助于相机光心和像素点构建, 并且向量运算需要在相同的参考坐标系下进行.
因为这些向量都以相机坐标系原点为起始点, 只需转换向量末端点到相应相机坐标系中.
| 在第一个相机坐标系 {a} 中描述 | 在第二个相机坐标系 {b} 中描述 | |
|---|---|---|
| 像素点 P a {\rm P}_a Pa | a p a {^ap_a} apa | b p a = R a p a + t {^bp_a} = {R}\, {^ap_a} + t bpa=Rapa+t |
| 像素点 P b {\rm P}_b Pb | a p b = a R b b p b + a t b = R T b p b + a t b {^ap_b} = {^aR_b}\, {^bp_b}+{^a t_b} = R^{\rm T} \, {^b p_b} +{^a t_b} apb=aRbbpb+atb=RTbpb+atb | b p b {^b p_b} bpb |
| {a} 与 {b} 相对位置 | a t b = − a R b t = − R T t {^at_b} = -{^aR_b} \, t = -R^{\rm T}\, t atb=−aRbt=−RTt | b t a = t {^bt_a} = t bta=t |
下面我们参考之前博文提前推导 [ R T t ] × [R^{\rm T}t]_{\times} [RTt]×.
假设任意三维向量 v v v, 则
[ c ] [ R T t ] × v = ( R T t ) × v = ( R T t ) × ( R T R v ) = R T ( t × R v ) = R T ( [ t ] × R v ) = R T [ t ] × R v (4-1) \begin{aligned}[c] [R^{\rm T}t]_{\times} v & = (R^{\rm T}t) {\times} v\\ & = (R^{\rm T}t) {\times} (R^{\rm T} R v)\\ & = R^{\rm T} (t \times R v)\\ & = R^{\rm T} ([t]_\times R v)\\ & = R^{\rm T} [t]_\times R v\\ \end{aligned} \tag{4-1} [c][RTt]×v=(RTt)×v=(RTt)×(RTRv)=RT(t×Rv)=RT([t]×Rv)=RT[t]×Rv(4-1)
因为对任意 v v v 成立, 故有
[ R T t ] × = R T [ t ] × R (4-2) [R^{\rm T}t]_{\times} = R^{\rm T} [t]_{\times} R \tag{4-2} [RTt]×=RT[t]×R(4-2)
5. 本质矩阵 (Essential Matrix)
在第一个相机坐标系 {a} 中, 因为对极约束的共面关系 ( O a O b → × O a P a → ) ⊥ O a P b → (\overrightarrow{O_a O_b} \times \overrightarrow{O_a P_a}) \, \bot \, \overrightarrow{O_a P_b} (OaOb×OaPa)⊥OaPb, 可知
a p b ⋅ ( a t b × a p a ) = 0 ⇒ ( R T b p b + a t b ) ⋅ ( a t b × a p a ) = 0 ⇒ ( R T b p b ) ⋅ ( a t b × a p a ) + a t b ⋅ ( a t b × a p a ) ⏟ = 0 = 0 ⇒ b p b T R ( [ R T t ] × a p a ) = 0 ⇒ b p b T R ( R T [ t ] × R a p a ) = 0 ⇒ b p b T [ t ] × R a p a = 0 (5-1) \begin{aligned} & ^ap_b \cdot (^at_b\times {^ap_a}) = 0 \\ \Rightarrow\qquad & (R^{\rm T} \, {^b p_b} +{^a t_b}) \cdot (^at_b\times {^ap_a}) = 0 \\ \Rightarrow\qquad & (R^{\rm T} \, {^b p_b}) \cdot (^at_b\times {^ap_a}) + \underset{=0}{\underbrace{{^a t_b} \cdot (^at_b\times {^ap_a})}} = 0 \\ \Rightarrow\qquad& {^bp_b^{\rm T}} R\, ([R^{\rm T} t]_\times {^ap_a}) = 0\\ \Rightarrow\qquad& {^bp_b^{\rm T}}\, R\, (R^{\rm T} [t]_{\times} R\, {^ap_a}) = 0\\ \Rightarrow\qquad& {^bp_b^{\rm T}}\, [t]_{\times} R\, {^ap_a} = 0 \end{aligned} \tag{5-1} ⇒⇒⇒⇒⇒apb⋅(atb×apa)=0(RTbpb+atb)⋅(atb×apa)=0(RTbpb)⋅(atb×apa)+=0 atb⋅(atb×apa)=0bpbTR([RTt]×apa)=0bpbTR(RT[t]×Rapa)=0bpbT[t]×Rapa=0(5-1)
同样地, 在第二个相机坐标系 {b} 中, 因为对极约束的共面关系 ( O b O a → × O b P a → ) ⊥ O b P b → (\overrightarrow{O_b O_a} \times \overrightarrow{O_b P_a}) \, \bot \, \overrightarrow{O_b P_b} (ObOa×ObPa)⊥ObPb, 可知
b p b ⋅ ( t × b p a ) = 0 ⇒ b p b ⋅ ( t × ( R a p a + t ) ) = 0 ⇒ b p b ⋅ ( t × ( R a p a ) ) = 0 ⇒ b p b T ( [ t ] × R a p a ) = 0 ⇒ b p b T [ t ] × R a p a = 0 (5-2) \begin{aligned} & ^bp_b \cdot (t\times {^bp_a}) = 0\\ \Rightarrow \qquad & ^bp_b \cdot \left(t\times ({R}\, {^ap_a} + t)\right) = 0\\ \Rightarrow \qquad & ^bp_b \cdot \left(t\times ({R}\, {^ap_a})\right) = 0\\ \Rightarrow \qquad & ^bp_b^{\rm T} \, ([t]_\times R \,{^ap_a}) = 0\\ \Rightarrow \qquad & ^bp_b^{\rm T} \, [t]_\times R \,{^ap_a} = 0\\ \end{aligned} \tag{5-2} ⇒⇒⇒⇒bpb⋅(t×bpa)=0bpb⋅(t×(Rapa+t))=0bpb⋅(t×(Rapa))=0bpbT([t]×Rapa)=0bpbT[t]×Rapa=0(5-2)
相同的共面约束, 在不同坐标系下推导, 得到了相同的方程式 (I-5-1) 和式 (I-5-2).
定义本质矩阵
E = [ t ] × R (5-3) E =[t]_{\times} R \tag{5-3} E=[t]×R(5-3)
则对极约束方程为
b p b T E a p a = 0 (5-4) ^bp_b^{\rm T} \,E\, {^ap_a} = 0 \tag{5-4} bpbTEapa=0(5-4)
该方程描述了同一场景点在不同相机坐标系下得到两个对应像素点的投影约束关系 —— 共平面关系 (Coplanarity).
默认像素点三维坐标在各自相机坐标系内描述, 对极约束方程进一步简写为
p b T E p a = 0 (5-5) p_b^{\rm T} \,E\, {p_a} = 0 \tag{5-5} pbTEpa=0(5-5)
6. 线坐标 (Coordinates of a Line)
图像平面 I a I_a Ia 上像素点 P a {\rm P}_a Pa 在相机坐标系 {a} 中的三维坐标
a p a = [ x a y a f ] (6-1) ^ap_a = \begin{bmatrix}x_a\\ y_a \\ f\end{bmatrix} \tag{6-1} apa= xayaf (6-1)
可以看做是二维的射影平面 I a I_a Ia 上的齐次坐标.
二维的射影平面上, 经过点 a p a ^ap_a apa 的直线方程可以表示为
l 1 x a + l 2 y a + l 3 f = 0 (6-2) l_1 x_a +l_2 y_a +l_3 f =0 \tag{6-2} l1xa+l2ya+l3f=0(6-2)
矢量
l = [ l 1 l 2 l 3 ] ∈ ( R 3 ∖ 0 ) (6-3) l = \begin{bmatrix} l_1\\ l_2\\ l_3\end{bmatrix} \in (\mathbb{R}^3 \setminus \mathbf{0}) \tag{6-3} l= l1l2l3 ∈(R3∖0)(6-3)
被称为直线的线坐标 (满足 l 1 , l 2 , l 3 l_1, l_2, l_3 l1,l2,l3 不同时为零). 比例因子 k ≠ 0 k \neq 0 k=0 时, 矢量 l l l 和矢量 k l k l kl 代表同一条直线.
进一步, 经过点 a p a ^ap_a apa 的二维直线方程简写为
l ⋅ a p a = 0 (6-4) l \cdot {^ap_a} = 0 \tag{6-4} l⋅apa=0(6-4)
此处 a p a ^ap_a apa 看作二维图像平面 I a I_a Ia 上的齐次坐标, 不是相机坐标系中的三维空间坐标.
7. 对极线 (Epipolar Lines)
如对极线示意图 Fig. 3 所示, 相机 a 与相机 b 光心的连线 O a O b ‾ \overline{O_a O_b} OaOb 称为基线, 基线 O a O b ‾ \overline{O_a O_b} OaOb 与场景中一点 P {\rm P} P 构成了对极平面 π \pi π. 如果相机 a 和 b 在空间中的位姿固定, 而场景点改变为 Q Q Q, 此时基线不变仍为 O a O b ‾ \overline{O_a O_b} OaOb, 而新的对极平面为 π Q \pi_Q πQ. 直观效果像是场景点牵着对极平面在绕基线转动.
基线与两个相机的成像平面的交点形成两个对极点. 基线 O a O b ‾ \overline{O_a O_b} OaOb 与相机 a 的成像平面 I a I_a Ia 相交的对极点为 a e b ^ae_b aeb, 看作是相机 b 的光心 O b O_b Ob 在相机 a 成像平面上的投影成像. 基线 O a O b ‾ \overline{O_a O_b} OaOb 与相机 b 的成像平面 I b I_b Ib 相交的对极点为 b e a ^be_a bea, 看作是相机 a 的光心 O a O_a Oa 在相机 b 成像平面上的投影成像. 如果相机 a 和 b 在空间中的位姿固定, 则形成的两个对极点也固定不变.
对极平面与两个相机的成像平面的相交形成两条对极线. 对极平面 π \pi π 与相机 a 的成像平面 I a I_a Ia 相交的对极线为 P a a e b ‾ \overline{P_a {^ae_b}} Paaeb, 极线经过对极点 a e b ^ae_b aeb 及场景点 P P P 在相机 a 成像平面上的投影点 P a {\rm P}_a Pa. 对极平面 π \pi π 与相机 b 的成像平面 I b I_b Ib 相交的对极线为 P b b e a ‾ \overline{P_b {^be_a}} Pbbea, 极线经过对极点 b e a ^be_a bea 及场景点 P P P 在相机 b 成像平面上的投影点 P b {\rm P}_b Pb. 对极线都经过成像平面上的对极点.
已知相机 a 中像素点/投影点 P a {\rm P}_a Pa, 在未知场景点 P \rm P P 确切位置的情况下, 根据射影关系, 只能猜测可能的场景点在反向投影线上, 可能为 P ′ ′ {\rm P}'' P′′、 P ′ {\rm P}' P′ 或 P \rm P P 等无穷多种情况之一. 那么像素点 P a {\rm P}_a Pa 对应的在相机 b 中的可能投影点/像素点为 P b {\rm P}_b Pb、 P b ′ {\rm P}_b' Pb′ 或 P b ′ ′ {\rm P}_b'' Pb′′ 等. 虽然成像平面 I b I_b Ib 上对应像素点是不确定的且有无穷多种可能性, 但这些候选点都在同一条直线上, 这条直线就是对极线. 利用对极线可以大大减小双目图像匹配的搜索空间, 不然需要在相机 b 成像平面 I b I_b Ib 全域搜索以匹配相机 a 上的一个像素点 P a {\rm P}_a Pa.
不同的场景点会改变成像平面内的像素点. 如场景点 P \rm P P 在两个相机内成像点为 P a {\rm P}_a Pa 和 P b {\rm P}_b Pb, 而场景点 Q \rm Q Q 在两个相机内成像点为 Q a {\rm Q}_a Qa 和 Q b {\rm Q}_b Qb. 那么对应的对极线也将改变. 但是两个相机位姿确定的情况下 (在世界坐标系中位姿固定), 两个对极点 a e b ^ae_b aeb 和 b e a ^be_a bea 的位置确定, 同时成像平面内的对极线必然经过该平面内的对极点. 所以不同的场景点在同一相机成像平面内形成了经过对极点的对极线束.

8. 对极线的线坐标 (Coordinates of Epipolar Lines)
由对极约束方程 (5-5), 我们定义
l ′ = E a p a (8-1) l' = E\, {^ap_a} \tag{8-1} l′=Eapa(8-1)
将 l ′ l' l′ 视为线坐标. 由式 (5-5) 可知
( E a p a ) ⋅ b p b = 0 (8-2) (E\, {^ap_a})\cdot {^bp_b} = 0 \tag{8-2} (Eapa)⋅bpb=0(8-2)
得到 l ′ l' l′ 经过 b p b ^bp_b bpb.
虽然对极点 b e a ^be_a bea 的坐标未知, 但是可以知道与 t t t 成正比, 即
b e a = κ t (8-3) ^be_a = \kappa\, t \tag{8-3} bea=κt(8-3)
代入
( E a p a ) ⋅ b e a = κ t ⋅ ( E a p a ) = κ t ⋅ ( [ t ] × R a p a ) = κ t ⋅ ( t × ( R a p a ) ⏟ ⊥ t ) = 0 (8-4) \begin{aligned} (E\, {^ap_a})\cdot {^be_a} &= \kappa \, t \cdot (E\, {^ap_a}) \\ &=\kappa \, t \cdot ([t]_{\times} R\, {^ap_a} ) \\ &=\kappa \, t \cdot (\underset{\bot t}{\underbrace{t\times (R \, {^ap_a})}} )\\ &= 0 \end{aligned} \tag{8-4} (Eapa)⋅bea=κt⋅(Eapa)=κt⋅([t]×Rapa)=κt⋅(⊥t t×(Rapa))=0(8-4)
得到 l ′ l' l′ 经过 b e a ^be_a bea.
既经过像素点 b p b ^bp_b bpb 又经过对极点 b e a ^be_a bea, 所以 l ′ = E a p a l' = E\, {^ap_a} l′=Eapa 是相机 b 成像平面 I b I_b Ib 内的对极线的线坐标.
默认像素点在各自相机坐标系内描述, 可简写为
l ′ = E p a (8-5) l' = E\, {p_a} \tag{8-5} l′=Epa(8-5)
类似地, 由对极约束方程 (5-5) 定义
l = E T b p b (8-6) l = E^{\rm T}\, {^bp_b} \tag{8-6} l=ETbpb(8-6)
由式 (5-5) 推导
l ⋅ a p a = ( E T b p b ) T a p a = b p b T E a p a = 0 (8-7) l \cdot {^ap_a} = \left(E^{\rm T}\, {^bp_b}\right)^{\rm T} {^ap_a} = {^bp_b^{\rm T}}\, E \, {^ap_a} = 0 \tag{8-7} l⋅apa=(ETbpb)Tapa=bpbTEapa=0(8-7)
得到 l l l 经过 a p a ^ap_a apa.
对极点 a e b ^ae_b aeb 在相机 a 内的坐标向量与 a t b ^at_b atb 成正比,
a e b = κ ′ a t b = − κ ′ R T t (8-8) {^ae_b} = \kappa' \, {^at_b} =- \kappa' \, R^{\rm T}\, t \tag{8-8} aeb=κ′atb=−κ′RTt(8-8)
代入计算
l ⋅ a e b = − κ ′ ( E T b p b ) T R T t = − κ ′ b p b T E R T t = − κ ′ b p b T [ t ] × R ⏟ = E R T t = − κ ′ b p b T [ t ] × t ⏟ = 0 = 0 (8-9) \begin{aligned} l\cdot {^ae_b} &= - \kappa' \left( E^{\rm T}\, {^bp_b} \right)^{\rm T} R^{\rm T}\, t \\ &= - \kappa' {^bp_b^{\rm T}} E R^{\rm T}\, t \\ &= - \kappa' {^bp_b^{\rm T}} \underset{=E}{\underbrace{[t]_{\times} R}} R^{\rm T}\, t \\ &= - \kappa' {^bp_b^{\rm T}} \underset{=0}{\underbrace{[t]_{\times} \, t}} \\ & = 0 \end{aligned} \tag{8-9} l⋅aeb=−κ′(ETbpb)TRTt=−κ′bpbTERTt=−κ′bpbT=E [t]×RRTt=−κ′bpbT=0 [t]×t=0(8-9)
得到 l l l 经过 a e b ^ae_b aeb.
既经过像素点 a p a ^ap_a apa 又经过对极点 a e b ^ae_b aeb, 所以 l = E T b p b l = E^{\rm T}\, {^bp_b} l=ETbpb 是相机 a 成像平面 I a I_a Ia 内的对极线的线坐标.
默认像素点在各自相机坐标系内描述, 可简写为
l = E T p b (8-10) l = E^{\rm T}\, {p_b} \tag{8-10} l=ETpb(8-10)
9. 本质矩阵的零空间 (Null Space of a Essential Matrix)
[性质 1] 当 t ≠ [ 0 , 0 , 0 ] T t\neq [0,0,0]^{\rm T} t=[0,0,0]T 时, 本质矩阵 E E E 的秩为 2, 即
r a n k ( E ) = 2 (9-1) {\rm rank}(E)=2 \tag{9-1} rank(E)=2(9-1)[性质 2] 对极点向量 a e b ^ae_b aeb 张成的一维空间是本质矩阵 E E E 的零空间.
[性质 3] 对极点向量 b e a ^be_a bea 张成的一维空间是本质矩阵 E E E 的左零空间.
[性质 1] 的说明:
det ( E ) = det ( [ t ] × R ) = det ( [ t ] × ) ⏟ = 0 det ( R ) ⏟ = 1 = 0 (9-2) \det(E) =\det([t]_{\times} R)= \underset{=0}{\underbrace{\det([t]_\times)}} \,\underset{=1}{\underbrace{\det(R)}} = 0 \tag{9-2} det(E)=det([t]×R)==0 det([t]×)=1 det(R)=0(9-2)
可知本质矩阵 E E E 是退化的.
又因为 r a n k ( [ t ] × ) = 2 {\rm rank}([t]_{\times})=2 rank([t]×)=2 且 R R R 为旋转矩阵可逆, 故 r a n k ( E ) = r a n k ( [ t ] × R ) = 2 {\rm rank}(E)={\rm rank}([t]_{\times}R) = 2 rank(E)=rank([t]×R)=2.
[性质 2] 的说明:
由式 (8-9) 可知, 相机 a 成像平面 I a I_a Ia 内的对极线 l l l 满足
l ⋅ a e b = ( E T b p b ) ⋅ a e b = 0 ⇒ b p b T ( E a e b ) = 0 (9-3) l \cdot {^ae_b} = \left(E^{\rm T}\, {^bp_b}\right) \cdot {^ae_b} = 0 \\ \Rightarrow \qquad {^bp_b^{\rm T}}\, (E \,{^ae_b}) = 0 \tag{9-3} l⋅aeb=(ETbpb)⋅aeb=0⇒bpbT(Eaeb)=0(9-3)
我们已知只要两个相机的在世界坐标系中的位姿固定, 不管场景点 P \rm P P 及其投影点 a p a ^ap_a apa 和 b p b ^bp_b bpb 如何变化, 相机 a 成像平面内的对极线 l l l 都经过对极点 a e b ^ae_b aeb. 所以 b p b ^bp_b bpb 可以任意变换, 上式总成立. 故有
E a e b = 0 (9-4) E \,{^ae_b} = 0 \tag{9-4} Eaeb=0(9-4)
说明了 “对极点向量 a e b ^ae_b aeb 张成的一维空间是本质矩阵 E E E 的零空间”.
[性质 3] 的说明:
同理, 由式 (8-4) 可知, 相机 b 成像平面 I b I_b Ib 内的对极线 l ′ l' l′ 满足
( E a p a ) ⋅ b e a = 0 ⇒ a p a T ( E T b e a ) = 0 (9-5) (E\, {^ap_a})\cdot {^be_a} = 0 \\ \Rightarrow\qquad {^ap_a^{\rm T}}\, (E^{\rm T}\, {^be_a}) = 0 \tag{9-5} (Eapa)⋅bea=0⇒apaT(ETbea)=0(9-5)
只要两个相机的在世界坐标系中的位姿固定, a p a ^ap_a apa 任意变化, 对极线总经过对极点, 上式总成立. 故有
E T b e a = 0 (9-6) E^{\rm T}\, {^be_a} = 0 \tag{9-6} ETbea=0(9-6)
说明了 “对极点向量 b e a ^be_a bea 张成的一维空间是本质矩阵 E E E 的左零空间”.
10. 本质矩阵的奇异值 (Singular Values of a Essential Matrix)
[性质 4] 本质矩阵 E E E 具有两个相等的非零奇异值, 以及一个零奇异值.
[性质 5] 对极点向量 b e a ^be_a bea 正比于本质矩阵 E E E 的零奇异值对应的左奇异向量 u 3 u_3 u3.
[性质 6] 对极点向量 a e b ^ae_b aeb 正比于本质矩阵 E E E 的零奇异值对应的右奇异向量 v 3 v_3 v3.
[性质 4] 的说明:
奇异值基本性质参考之前博文——奇异值分解之常用结论. 本质矩阵 E E E 的奇异值通过对称矩阵 E E T E\,E^{\rm T} EET 非零特征值的开平方来获得. 先计算 E E T E\,E^{\rm T} EET 的特征值.
det ( λ I − E E T ) = det ( λ I − [ t ] × R R T [ t ] × T ) = det ( λ I − [ t ] × [ t ] × T ) = − λ ( λ − t z 2 − t y 2 − t x 2 ) 2 (10-1) \begin{aligned} &\det(\lambda I- E\, E^{\rm T}) \\ =\; & \det(\lambda I- [t]_{\times} R\, R^{\rm T}\,[t]_{\times}^{\rm T}) \\ = \; &\det(\lambda I- [t]_{\times} \,[t]_{\times}^{\rm T}) \\ = \; & -\lambda\,(\lambda -t_z^2 - t_y^2 - t_x^2)^2 \end{aligned} \tag{10-1} ===det(λI−EET)det(λI−[t]×RRT[t]×T)det(λI−[t]×[t]×T)−λ(λ−tz2−ty2−tx2)2(10-1)
故 E E T E\,E^{\rm T} EET 的特征值为
{ λ 1 , 2 = t z 2 + t y 2 + t x 2 λ 3 = 0 (10-2) \left\{\begin{aligned} \lambda_{1,2} &= t_z^2 + t_y^2 + t_x^2 \\ \lambda_3 &= 0 \end{aligned} \right. \tag{10-2} {λ1,2λ3=tz2+ty2+tx2=0(10-2)
本质矩阵 E E E 的奇异值为
{ σ 1 , 2 = t z 2 + t y 2 + t x 2 σ 3 = 0 (10-3) \left\{\begin{aligned} \sigma_{1,2} &= \sqrt{t_z^2 + t_y^2 + t_x^2} \\ \sigma_3 &= 0 \end{aligned}\right. \tag{10-3} ⎩ ⎨ ⎧σ1,2σ3=tz2+ty2+tx2=0(10-3)
[性质 5] 的说明:
对称矩阵 E E T E\,E^{\rm T} EET 的特征向量 u 1 , u 2 , u 3 u_1, u_2, u_3 u1,u2,u3 构成了本质矩阵 E E E 的左奇异向量.
已知对称矩阵 E E T E\,E^{\rm T} EET 的特征值中只有一个零特征值, 所以 E E T E\,E^{\rm T} EET 的零空间是 1 维的.
由式 (9-6) 可知
E E T b e a = E ( E T b e a ) = 0 (10-4) E\,E^{\rm T}\, {^be_a} = E\,(E^{\rm T}\, {^be_a}) = 0 \tag{10-4} EETbea=E(ETbea)=0(10-4)
又由特征值和特征向量关系
E E T u 3 = λ 3 u 3 = 0 (10-5) E\,E^{\rm T} u_3 = \lambda_3 \,u_3 = 0 \tag{10-5} EETu3=λ3u3=0(10-5)
可知 b e a ^be_a bea 和 u 3 u_3 u3 都在 E E T E\,E^{\rm T} EET 的 1 维零空间上, 所以 “对极点向量 b e a ^be_a bea 正比于本质矩阵 E E E 的零奇异值对应的左奇异向量 u 3 u_3 u3”.
[性质 6] 的说明:
首先说明 E E T E\,E^{\rm T} EET 与 E T E E^{\rm T}E ETE 之间是相似.
已知 [ t ] × T = − [ t ] × [t]_{\times}^{\rm T} = -[t]_{\times} [t]×T=−[t]×, 及 E E T = [ t ] × R R T [ t ] × T = [ t ] × [ t ] × T E\, E^{\rm T} = [t]_{\times} R\, R^{\rm T}\,[t]_{\times}^{\rm T} = [t]_{\times} \,[t]_{\times}^{\rm T} EET=[t]×RRT[t]×T=[t]×[t]×T, 则
E T E = ( [ t ] × R ) T [ t ] × R = R T [ t ] × T [ t ] × R = R T [ t ] × [ t ] × T R = R T E E T R (10-6) \begin{aligned} E^{\rm T} E &= \left([t]_{\times} R\right)^{\rm T}\, [t]_{\times} R\\ &= R^{\rm T} [t]_{\times}^{\rm T}\, [t]_{\times} R \\ &= R^{\rm T} [t]_{\times} [t]_{\times}^{\rm T} R \\ &= R^{\rm T} E \, E^{\rm T} R \end{aligned} \tag{10-6} ETE=([t]×R)T[t]×R=RT[t]×T[t]×R=RT[t]×[t]×TR=RTEETR(10-6)
旋转矩阵 R R R 是可逆的, 故有矩阵相似关系 E E T ∼ E T E E\,{E^{\rm T}} \sim {E^{\rm T}} E EET∼ETE. 相似矩阵的特征值相同.
对称矩阵 E T E E^{\rm T}E ETE 的特征向量 v 1 , v 2 , v 3 v_1, v_2, v_3 v1,v2,v3 构成了本质矩阵 E E E 的右奇异向量.
由式 (9-4) 可知
E T E a e b = E T ( E a e b ) = 0 (10-7) E^{\rm T}\, E \,{^ae_b} = E^{\rm T}\,(E \,{^ae_b}) = 0 \tag{10-7} ETEaeb=ET(Eaeb)=0(10-7)
又由于
E T E v 3 = λ 3 v 3 = 0 (10-8) E^{\rm T}E\, v_3 = \lambda_3 \, v_3 = 0 \tag{10-8} ETEv3=λ3v3=0(10-8)
同时由于 E T E E^{\rm T}\, E ETE 只有一个零特征值, E T E E^{\rm T}\, E ETE 零空间是 1 维的.
可知 a e b ^ae_b aeb 和 v 3 v_3 v3 都在 E T E E^{\rm T}E ETE 的 1 维零空间上, 所以 “对极点向量 a e b ^ae_b aeb 正比于本质矩阵 E E E 的零奇异值对应的右奇异向量 v 3 v_3 v3”.
总结
如有问题或者错误, 请不吝指教, 谢谢!
参考文献
[1] Carlo Tomasi, Epipolar Geometry and the Essential Matrix, https://courses.cs.duke.edu/spring20/compsci527/notes/epipolar-geometry.pdf
[2] 熊有伦等, 机器人学: 建模、控制与视觉, 华中科技大学出版社, 2020
版权声明:本文为博主原创文章,遵循 CC 4.0 BY 版权协议,转载请附上原文出处链接和本声明。
本文链接:https://blog.csdn.net/woyaomaishu2/article/details/141973232
本文作者:wzf@robotics_notes
相关文章:

对极约束及其性质 —— 公式详细推导
Title: 对极约束及其性质 —— 公式详细推导 文章目录 前言1. 对极约束 (Epipolar Constraint)2. 坐标转换 (Coordinate Transformations)3. 像素坐标 (Pixel Coordinates)4. 像素坐标转换 (Transformations of Pixel Coordinates)5. 本质矩阵 (Essential Matrix)6. 线坐标 (Co…...

【论文精读】SCINet-基于降采样和交互学习的时序卷积模型
《SCINet: Time Series Modeling and Forecasting with Sample Convolution and Interaction》的作者团队来自香港中文大学,发表在NeurIPS 2022会议上。 动机 该论文的出发点是观察到时间序列数据具有独特的属性:即使在将时间序列下采样成两个子序列后,时间关系(例如数据…...
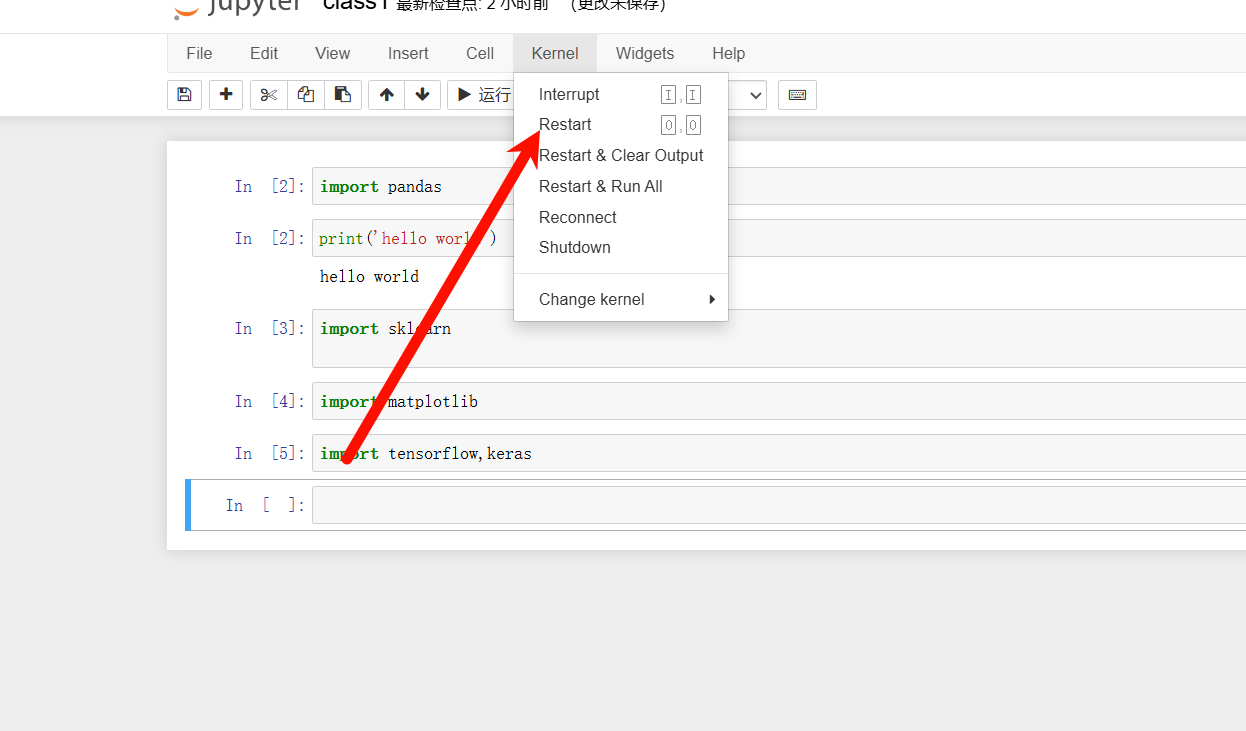
深度学习与大模型第1课环境搭建
文章目录 深度学习与大模型第1课环境搭建1. 安装 Anaconda2. 修改环境变量2.1 修改 .condarc 文件2.2 使用 Anaconda Prompt 修改环境变量 3. 新建 .ipynb 文件 机器学习基础编程:常见问题: 深度学习与大模型第1课 环境搭建 1. 安装 Anaconda 首先&am…...

JDK新特性
LTS Record jdk16 不是方法 是一个定 # Sealed Class/Interface jdk17 限制只能由某些类继承 CompletableFuture jkd8 PatternMatching of instanceOf jdk16 switch expressions jdk14 Stream.collect() Collector Collector API Collector.groupBy Collector实战 1. …...

数据处理与数据填充在Pandas中的应用
在数据分析和机器学习项目中,数据处理是至关重要的一步。Pandas作为Python中用于数据分析和操作的一个强大库,提供了丰富的功能来处理和清洗数据。本文将深入探讨Pandas在数据处理,特别是数据填充方面的应用。 在实际的数据集中,…...
)
【百日算法计划】:每日一题,见证成长(010)
题目 合并两个排序的链表 输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的 示例1: 输入:1->2->4, 1->3->4 输出:1->1->2->3->4->4 思路 引入一个带虚拟头结点和tail指针的…...

【WPF】WPF学习之【二】布局学习
WPF布局学习 常用布局Grid网格布局StackPanel 布局CanvasDockPanel布局WrapPanel布局 常用布局 1、StackPanel: 学习如何使用StackPanel进行垂直和水平布局。 2、Grid: 掌握Grid的网格布局技术。 3、Canvas: 了解Canvas的绝对定位布局。 4、DockPanel: 学习DockPanel的停靠…...

KEIL中编译51程序 算法计算异常的疑问
KEIL开发 51 单片机程序 算法处理过程中遇到的问题 ...... by 矜辰所致前言 因为产品的更新换代, 把所有温湿度传感器都换成 SHT40 ,替换以前的 SHT21。在 STM32 系列产品上的替换都正常,但是在一块 51 内核的无线产品上面,数据…...

pikachu文件包含漏洞靶场
本地文件包含 1、先随意进行提交 可以得出是GET传参 可以在filename参数进行文件包含 2、准备一个2.jpg文件 内容为<?php phpinfo();?> 3、上传2.jpg文件 4、访问文件保存的路径uploads/2.jpg 5、将我们上传的文件包含进来 使用../返回上级目录 来进行包含木马文件 …...

基于DPU与SmartNIC的K8s Service解决方案
1. 方案背景 1.1. Kubernetes Service介绍 Kubernetes Service是Kubernetes中的一个核心概念,它定义了一种抽象,用于表示一组提供相同功能的Pods(容器组)的逻辑集合,并提供了一种方式让这些Pods能够被系统内的其他组…...

SLM561A系列 60V 10mA到50mA线性恒流LED驱动芯片 为智能家居照明注入新活力
SLM561A系列选型参考: SLM561A10ae-7G SOD123 SLM561A15ae-7G SOD123 SLM561A20ae-7G SOD123 SLM561A25ae-7G SOD123 SLM561A30ae-7G SOD123 SLM561A35ae-7G SOD123 SLM561A40ae-7G SOD123 SLM561A45ae-7G SOD123 SLM561A50ae-7G SOD123 …...

Requests库对session的支持
场景:如何获取登录时响应消息中的sessionid,以及如何在后续请求中把sessionid添到cookie中 Requests库提供了一个Session类,通过requests库中的session对象,requests库会自动帮我们保存服务端返回的cookie数据(set-cookie里的内容…...

利用深度学习实现验证码识别-2-使用Python导出ONNX模型并在Java中调用实现验证码识别
1. Python部分:导出ONNX模型 首先,我们需要在Python中定义并导出一个已经训练好的验证码识别模型。以下是完整的Python代码: import string import torch import torch.nn as nn import torch.nn.functional as FCHAR_SET string.digits# …...

如何通过Spring Cloud Consul增强微服务安全性和可靠性
为了增强微服务的安全性和可靠性,Spring Cloud Consul 是一个非常强大的工具。它不仅提供了服务发现和配置管理功能,还能够有效地管理微服务的安全和健康状态。本文将深入探讨如何通过 Spring Cloud Consul 来增强微服务的安全性和可靠性,主要…...

无代码搭建小程序zion
无代码搭建小程序zion 一、无代码搭建小程序zion的降低技术门槛,提升开发效率 1. 无需编程经验:Zion无代码平台通过提供直观的可视化界面和拖拽式操作,让开发者无需具备复杂的编程技能也能进行小程序的开发。这种方式大大降低了技术门槛&a…...

【南方科技大学】CS315 Computer Security 【Lab1 Packet Sniffing and Wireshark】
目录 IntroductionBackgroundTCP/IP Network StackApplication LayerTransport LayerInternet LayerLink LayerPacket Sniffer Getting WiresharkStarting WiresharkCapturing PacketsTest Run Questions for the Lab Introduction 实验的第一部分介绍数据包嗅探器 Wireshark。…...

【人工智能/机器学习/机器人】数学基础-学习笔记
函数 奇偶性: 偶函数: f ( − x ) f ( x ) f(-x)f(x) f(−x)f(x) y轴对称 f ( x ) x 2 f(x)x^2 f(x)x2 f ( − x ) ( − x ) 2 x 2 f ( x ) f(-x)(-x)^2x^2f(x) f(−x)(−x)2x2f(x) 奇函数: f ( − x ) − f ( x ) f(-…...
视频安防监控LntonAIServer安防管理平台抖动检测和过亮过暗检测
随着视频监控技术的发展,视频质量成为确保监控系统有效性的重要因素。LntonAIServer通过引入抖动检测与过亮过暗检测功能,进一步提升了视频监控系统的可靠性和用户体验。这些功能可以帮助及时发现并解决视频流中的质量问题,确保视频监控系统始…...

网络模型及协议介绍
一.OSI七层模型 OSI Open System Interconnect 开放系统互连模型 以前不同厂家所生产的网络设备的标准是不同的,所以为了统一生产规范就制定了OSI这个生产模型。 作用:降低网络进行数据通信复杂度 这个模型的作用第一降低数据通信的复杂度ÿ…...

手撕HashMap源码
终于通过不屑努力,把源码中的重要部分全都看完了,每一行代码都看明白了,还写了注释 import java.lang.reflect.ParameterizedType; import java.lang.reflect.Type; import java.util.*; import java.util.function.Consumer; import java.ut…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...
