【人工智能/机器学习/机器人】数学基础-学习笔记
函数
奇偶性:
-
偶函数: f ( − x ) = f ( x ) f(-x)=f(x) f(−x)=f(x) y轴对称
f ( x ) = x 2 f(x)=x^2 f(x)=x2 f ( − x ) = ( − x ) 2 = x 2 = f ( x ) f(-x)=(-x)^2=x^2=f(x) f(−x)=(−x)2=x2=f(x) -
奇函数: f ( − x ) = − f ( x ) f(-x)=-f(x) f(−x)=−f(x) 原点对称
f ( x ) = x 3 f(x)=x^3 f(x)=x3 f ( − x ) = ( − x ) 3 = − x 3 = − f ( x ) f(-x)=(-x)^3=-x^3=-f(x) f(−x)=(−x)3=−x3=−f(x) -
周期性: f ( x + T ) = f ( x ) f(x+T)=f(x) f(x+T)=f(x)
-
单调性:
-

极限
数列
按照一定次数排列的一列数: u 1 , u 2 , u 3 , ⋅ ⋅ ⋅ , u n , ⋅ ⋅ ⋅ u_1,u_2,u_3,···,u_n,··· u1,u2,u3,⋅⋅⋅,un,⋅⋅⋅,其中 u n u_n un叫做通项
对于数列 { u n } \{u_n\} {un},如果当 n n n无限大时,其通项无限接近于一个参数 A A A
则称该数列以 A A A为极限或称数列收敛于 A A A,否则称数列为发散
lim n → ∞ u n = A \lim\limits_ {n \to \infty}u_n=A n→∞limun=A ,或 u n → A ( n → ∞ ) u_n \to A (n \to \infty) un→A(n→∞)
lim n → ∞ 1 3 n = 0 \lim\limits_{n \to \infty}{\frac 1{3^n}}=0 n→∞lim3n1=0, lim n → ∞ n n + 1 = 1 \lim\limits_{n \to \infty}{ \frac n{n+1}}=1 n→∞limn+1n=1, lim n → ∞ 2 n \lim\limits_{n \to \infty}2^n n→∞lim2n不存在
极限
符号表示:
x → ∞ x \to \infty x→∞表示“当 ∣ x ∣ |x| ∣x∣无限增大时”;
x → + ∞ x \to +\infty x→+∞表示“当 x x x无限增大时”;
x → − ∞ x \to -\infty x→−∞表示“当 x x x无限减少时”;
x → x 0 x \to x_0 x→x0表示“当 x x x从 x 0 x_0 x0的左右两侧无限接近于 x 0 x_0 x0时”;
x → x 0 + x \to x^+_0 x→x0+表示“当 x x x从 x 0 x_0 x0的右侧无限接近于 x 0 x_0 x0时”;
x → x 0 − x \to x^-_0 x→x0−表示“当 x x x从 x 0 x_0 x0的左侧无限接近于 x 0 x_0 x0时”;

- 函数在 x 0 x_0 x0的邻域内有定义, lim x → x 0 f ( x ) = A \lim\limits_{x \to x_0}f(x)=A x→x0limf(x)=A,或 f ( x ) → A ( x → x 0 ) f(x) \to A(x \to x_0) f(x)→A(x→x0)
lim x → 1 x 2 − 1 x − 1 = lim x → 1 ( x − 1 ) ( x + 1 ) x − 1 = 2 \lim\limits_{x \to 1}{\frac {x^2-1}{x-1}}=\lim\limits_{x \to 1}{\frac {(x-1)(x+1)}{x-1}}=2 x→1limx−1x2−1=x→1limx−1(x−1)(x+1)=2 - 左右极限:函数在左半邻域 ( x 0 − δ , x 0 ) (x_0-\delta,x_0) (x0−δ,x0)或右半邻域 ( x 0 , x 0 + δ ) (x_0,x_0+\delta) (x0,x0+δ)内有定义
lim x → x 0 + f ( x ) = A \lim\limits_{x \to x^+_0}f(x)=A x→x0+limf(x)=A,或 f ( x ) → A ( x → x 0 + ) f(x) \to A(x \to x^+_0) f(x)→A(x→x0+)或 f ( x 0 + 0 ) = A f(x_0+0)=A f(x0+0)=A
lim x → x 0 − f ( x ) = A \lim\limits_{x \to x^-_0}f(x)=A x→x0−limf(x)=A,或 f ( x ) → A ( x → x 0 − ) f(x) \to A(x \to x^-_0) f(x)→A(x→x0−)或 f ( x 0 − 0 ) = A f(x_0-0)=A f(x0−0)=A
持续更新!!!!!
相关文章:

【人工智能/机器学习/机器人】数学基础-学习笔记
函数 奇偶性: 偶函数: f ( − x ) f ( x ) f(-x)f(x) f(−x)f(x) y轴对称 f ( x ) x 2 f(x)x^2 f(x)x2 f ( − x ) ( − x ) 2 x 2 f ( x ) f(-x)(-x)^2x^2f(x) f(−x)(−x)2x2f(x) 奇函数: f ( − x ) − f ( x ) f(-…...
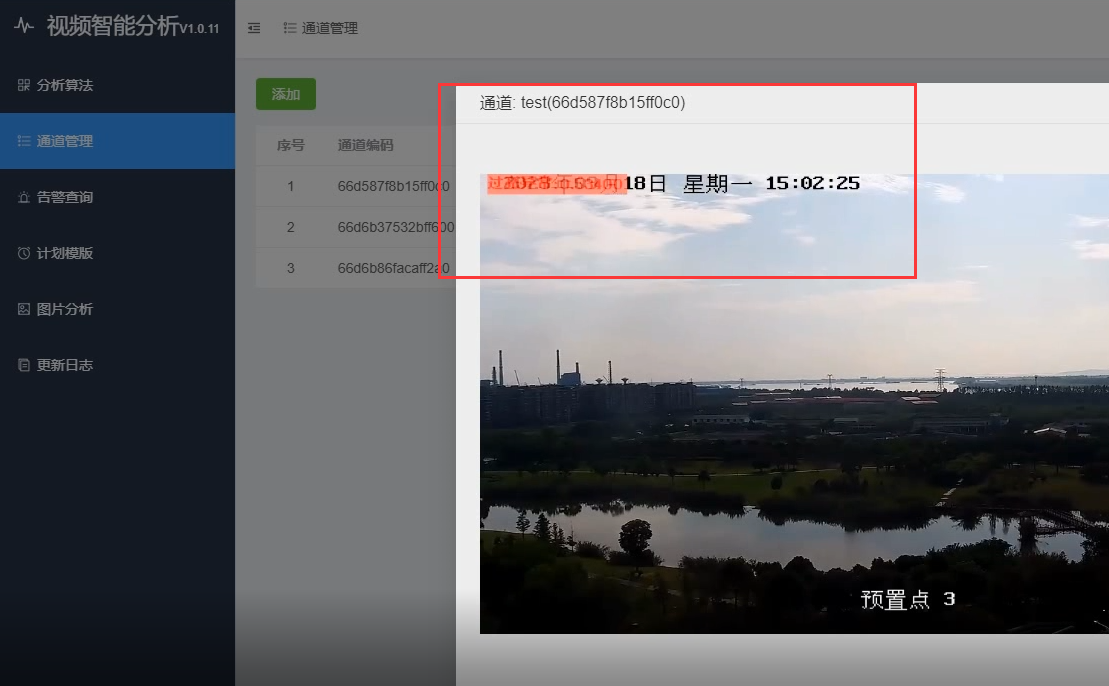
视频安防监控LntonAIServer安防管理平台抖动检测和过亮过暗检测
随着视频监控技术的发展,视频质量成为确保监控系统有效性的重要因素。LntonAIServer通过引入抖动检测与过亮过暗检测功能,进一步提升了视频监控系统的可靠性和用户体验。这些功能可以帮助及时发现并解决视频流中的质量问题,确保视频监控系统始…...

网络模型及协议介绍
一.OSI七层模型 OSI Open System Interconnect 开放系统互连模型 以前不同厂家所生产的网络设备的标准是不同的,所以为了统一生产规范就制定了OSI这个生产模型。 作用:降低网络进行数据通信复杂度 这个模型的作用第一降低数据通信的复杂度ÿ…...

手撕HashMap源码
终于通过不屑努力,把源码中的重要部分全都看完了,每一行代码都看明白了,还写了注释 import java.lang.reflect.ParameterizedType; import java.lang.reflect.Type; import java.util.*; import java.util.function.Consumer; import java.ut…...

OceanBase block_file与log过大 的问题
一、说明 block_file 是存放sstable的数据文件,由datafile_disk_percentage 参数与datafile_size参数决定,两个参数同时配置,以datafile_size为主。 datafile_disk_percentage 默认值是90 datafile_size 默认值是0M到正无穷 因为block_file 的…...

【Focal Loss 本质】
Focal Loss 示例 Focal Loss公式: 在后面的例子中,我们假定 y 1 的样本中,有两个预测值分别为(0.8, 0.4)。显然,0.8 很容易分类,0.4 很难分类。 可以看出,Focal Loss 降低了容易分类(prt 0…...
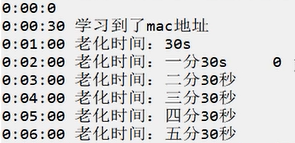
端口安全老化细节
我们都知道port-security aging-time命令用来配置端口安全动态MAC地址的老化时间,但是后面还可以加上类型: [SW1-GigabitEthernet0/0/1]port-security aging-time 5 type absolute Absolute time 绝对老化 inactivity Inactivity time相对老化 …...

【C++】—— string 模拟实现
【C】—— string模拟实现 0 前言1 string的底层结构2 默认成员函数的实现2.1 构造函数2.1.1 无参构造2.1.2 带参构造2.1.2 合并 2.2 析构函数2.3 拷贝构造函数2.3.1 传统写法2.3.2 现代写法 2.3 赋值重载2.3.1 传统写法2.3.2 现代写法2.3.3 传统写法与现代写法的优劣 3 size、…...

详解TensorRT的C++高性能部署以及C++部署Yolo实践
详解TensorRT的C高性能部署 一. ONNX1. ONNX的定位2. ONNX模型格式3. ONNX代码使用实例 二、TensorRT1 引言 三、C部署Yolo模型实例 一. ONNX 1. ONNX的定位 ONNX是一种中间文件格式,用于解决部署的硬件与不同的训练框架特定的模型格式的兼容性问题。 ONNX本身其…...

手机如何切换网络IP地址:方法详解与操作指南
在当今的数字化时代,网络IP地址作为设备在网络中的唯一标识,扮演着至关重要的角色。对于手机用户而言,了解如何切换网络IP地址不仅有助于提升网络体验,还能在一定程度上保护个人隐私。本文将详细介绍手机切换网络IP地…...
南通网站建设手机版网页
随着移动互联网的迅猛发展,越来越多的人通过手机浏览网页,进行在线购物、信息查询和社交互动。因此,建立一个适合移动端访问的网站已成为企业和个人不可忽视的重要任务。在南通,网站建设手机版网页的需求逐渐增加,如何…...

macos系统内置php文件列表 系统自带php卸载方法
在macos系统中, 自带已经安装了php, 根据不同的macos版本php的版本号可能不同, 我们可以通过 which php 命令来查看mac自带的默认php安装路径, 不过注意这个只是php的执行文件路径. 系统自带php文件列表 一下就是macos默认安装的php文件列表. macos 10.15内置PHP文件列表配置…...

微信小程序认证和备案
小程序备案的流程一般包括以下步骤: 准备备案所需材料:通常需要提供营业执照、法人的身份证、两个手机号和一个邮箱等资料。 1 登录微信公众平台:作为第一次开发微信小程序的服务商,需要通过微信公众平台申请…...

C++复习day05
类和对象 1. 面向对象和面向过程的区别是什么?(开放性问题) 1. **抽象级别**:- **面向对象**:以对象(数据和方法的集合)为中心,强调的是数据和行为的封装。- **面向过程**…...

python数值误差
最近在用fenics框架跑有限元代码,其中有一个部分是把在矩阵里定义的初始值,赋值到有限元空间里,这就涉及到了初始矩阵和有限元空间坐标的转化,部分代码如下 for i in range(len(dof_coordinates)):# x, y dof_coordinates[i…...

基于FPGA的OV5640摄像头图像采集
1.OV5640简介 OV5640是OV(OmniVision)公司推出的一款CMOS图像传感器,实际感光阵列为:2592 x 1944(即500w像素),该传感器内部集成了图像出炉的电路,包括自动曝光控制(AEC…...

CDN ❀ Http协议标准缓存字段梳理
文章目录 1. 背景介绍2. 测试环境搭建3. 缓存字段3.1 Expires3.2 Cache-Control3.3 协商缓存 1. 背景介绍 Http协议标准有RFC定义好的请求和响应头部字段用于进行缓存设置,本文主要进行介绍缓存功能相关的头部字段及其使用方法。在使用CDN功能是,协议标…...

浅谈NODE的NPM命令和合约测试开发工具HARDHAT
$ npm install yarn -g # 将模块yarn全局安装 $ npm install moduleName # 安装模块到项目目录下 默认跟加参数 --save 一样 会在package文件的dependencies节点写入依赖。 $ npm install -g moduleName # -g 的意思是将模块安装到全局,具体安装到磁盘哪个位置&…...
)
k8s-pod 实战六 (如何在不同的部署环境中调整startupprobe的参数?)
在不同的部署环境中(如开发、测试、生产环境),你可能希望对 startupProbe 的参数进行调整,以适应不同的需求和条件。以下是几种常见的方法和实践: 方法一:使用 Kustomize 1. 目录结构 假设你的项目目录结构如下: my-app/ ├── base/ │ └── deployment.yaml …...

和服务端系统的通信
首先web网站 前端浏览器 和 后端系统 是通过HTTP协议进行通信的 同步请求&异步请求: 同步请求:可以从浏览器中直接获取的(HTML/CSS/JS这样的静态文件资源),这种获取请求的http称为同步请求 异步请求:js代码需要到服…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...
