力扣接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5] 输出:9
提示:
n == height.length1 <= n <= 2 * 1040 <= height[i] <= 105
动态规划:
class Solution {public int trap(int[] height) {int len = height.length;// 如果数组长度为0,返回0if(len == 0){return 0;}// 创建一个数组用于存储每个位置左侧的最大高度int[] leftMax = new int[len];for(int i = 1; i < len; i++){// 更新当前点的左侧最大高度leftMax[i] = Math.max(height[i-1], height[i]);}// 创建一个数组用于存储每个位置右侧的最大高度int[] rightMax = new int[len];for(int i = len-2; i >= 0; i--){// 更新当前点的右侧最大高度rightMax[i] = Math.max(height[i], height[i+1]);}int ans = 0;// 计算每个位置能够存储的水量for(int i = 0; i < len; i++){ans += Math.min(leftMax[i], rightMax[i]) - height[i];}// 返回能够存储的总水量return ans;}
}
单调栈解决
import java.util.Stack;class Solution {public int trap(int[] height) {// 初始化总雨水量为0int totalWater = 0;// 创建一个栈用于存储数组索引Stack<Integer> stack = new Stack<>();// 遍历每个高度for (int i = 0; i < height.length; i++) {// 当栈非空且当前高度大于栈顶所指的高度时while (!stack.isEmpty() && height[i] > height[stack.peek()]) {// 取出栈顶的高度索引int top = stack.pop();// 如果栈为空,跳出循环if (stack.isEmpty()) {break;}// 计算当前柱子的宽度int distance = i - stack.peek() - 1;// 计算能形成的水位高度差int boundedHeight = Math.min(height[i], height[stack.peek()]) - height[top];// 计算当前能积的水量并加到总水量中totalWater += distance * boundedHeight;}// 将当前索引入栈stack.push(i);}// 返回总雨水量return totalWater;}
}
工作原理
- 单调递减栈:栈中存储的是高度数组的索引。栈内元素对应的高度从栈底到栈顶是非递增的。
- 遍历高度数组:对于每一个高度,若其大于栈顶元素所指的高度(即找到一个可能的凹槽),则计算当前凹槽的水量。
- 水量计算:
- 宽度:凹槽宽度为当前索引
i与栈顶下一个元素的索引之差再减去 1。 - 高度:水位高度差为
min(当前高度, 栈顶下一个高度) - 栈顶高度。
- 宽度:凹槽宽度为当前索引
- 累加水量:将计算出的水量累加到总水量中。
在计算接雨水的过程中,水的高度取决于柱子之间的最低高度。具体来说,水只能被较矮的柱子挡住。因此,关键在于找到最低的柱子,并根据它来计算可能存储的水量。
class Solution {public int trap(int[] height) {int len=height.length;int left=0,right=len-1;int leftMax=0,rightMax=0;int ans=0;while(left<=right){leftMax=Math.max(leftMax,height[left]);rightMax=Math.max(rightMax,height[right]);if(height[left]<height[right]){ans+=leftMax-height[left];left++;}else{ans +=rightMax-height[right];right--;}}return ans;}
}判断逻辑
-
水量计算基础:
- 对于
height[left] < height[right]的情况,由于leftMax是从左侧移动过程中遇到的最大高度,而rightMax是从右侧移动过程中遇到的最大高度,因此:- 当前柱子
height[left]左侧的最大高度leftMax是可靠的。 - 但是,右侧的最大高度
rightMax还可能会更新。因此,此时计算left位置的积水量是安全的。
- 当前柱子
- 对于
-
为什么选择较小的高度:
- 如果
height[left] < height[right],意味着在当前位置left,其右侧有更高的柱子。这个较高的柱子可以帮助挡住雨水。因此可以确定leftMax是最小的限制条件,用它来计算当前位置可能存储的水量是安全的。 - 如果
height[left] >= height[right],那么右侧柱子在此时成为决定因素,左侧的leftMax没有影响,应该通过rightMax计算右侧的水量。
- 如果
例子说明
假设 height[left] = 2,height[right] = 5:
-
当
left侧低于right侧:可以确定在左侧left柱子能容纳的水量只取决于leftMax。因此,将left向右移动并计算leftMax - height[left]。 -
如果反过来:如果左侧高于或等于右侧,则右侧可能会积水,因此移动
right向左并计算rightMax - height[right]。
总结
这一判断的核心在于:
- 小于:左侧可能有积水,计算左侧。
- 大于等于:右侧可能有积水,计算右侧。
初始状态下的 right 指针
right指针初始位置:它从数组的最右端开始。left指针初始位置:它从数组的最左端开始。
初始比较:height[left] < height[right]
在算法的开始阶段,我们用 height[left] < height[right] 来判断接下来的行动。虽然 right 一开始位于数组的最右边,但这并不影响算法的正确性,原因如下:
-
rightMax的初始化:- 初始时,
rightMax会等于height[right]。因为right指针在最右端,所以rightMax一开始就是数组最右边的那个高度。 - 随着
right指针向左移动,rightMax会逐渐更新为更大的值,直到遍历完所有右边的柱子。
- 初始时,
-
初始状态的判断:
- 在开始时,算法将
left和right的柱子高度进行比较。 - 如果
height[left] < height[right],说明左边的柱子比右边矮。在这种情况下,右边更高的柱子可以“挡住”水,因此左边柱子上方可能会有积水,这时候左边的积水高度是可以确定的,所以移动left指针并计算水量。 - 如果
height[left] >= height[right],算法会移动right指针。此时,不会计算left指针位置的积水,而是继续查看右边的柱子是否可能形成积水。
- 在开始时,算法将
-
意义在于确定安全的水量:
- 通过比较
height[left]和height[right],算法确保了在当前位置计算水量时,有足够的信息保证水量是准确的。 rightMax和leftMax在算法执行过程中不断更新,确保算法总是在安全的条件下进行计算。
- 通过比较
实际意义
即使 right 指针最开始位于最右边,这个初始比较也有意义,因为它为整个算法奠定了基础。我们可以通过这个初始比较,确保在移动 left 或 right 指针时,计算的积水量是正确且安全的。
举个例子
假设 height 数组为 [1, 0, 2, 1, 0, 1, 3],left 和 right 初始分别在位置 0 和 6:
left开始为1,right开始为3。- 第一次比较时,
height[left] = 1,height[right] = 3,显然1 < 3,我们可以放心地移动left指针,因为左边的积水高度确定不会超过leftMax。
总之,这一步比较对于算法的正确性和水量计算至关重要,即使 right 指针最初处于最右边,也依然有效且必要。
相关文章:

力扣接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表…...

bug“医典”
温馨提示:本篇文章主要用于收藏博主所遇到的各种bug,并且不定期更新 目录 未初始化 “病状” “处方” 数组越界 “病状” “处方” 未创建对象 “病状” 编辑 “处方” 未初始化 “病状” 这种是处在链表中的一种情况,通常是没有处理哨兵位…...

Track 06:量子计算机概述
量子计算机概述 量子计算机是基于量子力学原理的一种计算机,它与传统的经典计算机在处理信息的方式上有根本性的区别。量子计算机的设计和实现依赖于量子比特(qubits)和量子计算的核心概念,如叠加态和纠缠态,这些特性使其在解决某些复杂问题时具备传统计算机无法比拟的优…...

论文解读 | KDD2024 演化图上的森林矩阵快速计算
点击蓝字 关注我们 AI TIME欢迎每一位AI爱好者的加入! 点击 阅读原文 观看作者直播讲解回放! 作者简介 孙浩鑫,复旦大学博士生,主要研究方向为大规模图上快速算法设计。 概述 森林矩阵在网络科学、观点动力学和机器学习相关应用中…...
7.统一网关-Gateway
文章目录 1.统一网关介绍2.网关开发3.predicate4.Route Predicate Factories(路由断言工厂)4.1Path 路由断言工厂4.2.Method 路由断言工厂4.3 Header 路由断言工厂4.4 Query 路由断言工厂4.5 Host 路由断言工厂4.6 After 路由断言工厂4.7 Before 路由断言工厂4.8 Between 路由断…...

QT:QWidget 控件属性的介绍
控件属性介绍 🌴enabled 状态属性🌴geometry 几何属性示例一:改变控件尺寸示例二:更变控件位置window frame 的影响 🌴windowTitle 窗口标题🌴windowIcon 窗口图标🌴 qrc机制🌴windo…...

ctfshow-nodejs
什么是nodejs Node.js 是一个基于 Chrome V8 引擎的 Javascript 运行环境。可以说nodejs是一个运行环境,或者说是一个 JS 语言解释器 Nodejs 是基于 Chrome 的 V8 引擎开发的一个 C 程序,目的是提供一个 JS 的运行环境。最早 Nodejs 主要是安装在服务器…...

Linux 大文件和大量小文件的复制策略
在Linux上复制大文件或大量小文件时,可以根据文件的类型、数量以及硬件配置(如硬盘类型、CPU、内存)选择不同的复制策略,以提高复制效率。以下是一些常见的策略和工具,可以根据具体情况使用: 1. 大文件复制…...

0.3 学习Stm32经历过的磨难
文章目录 用库函数传参 能否按位或STM32库函数XXX_GetFlagStatus和XXX_GetITStatus的区别关于MDK导入文件后报错 Browse information of one files is not available用exti中断读取按键 忘记消抖 (更离谱的是,我忘记开启afio的时钟了 Damn!)D…...
9、Django Admin优化查询
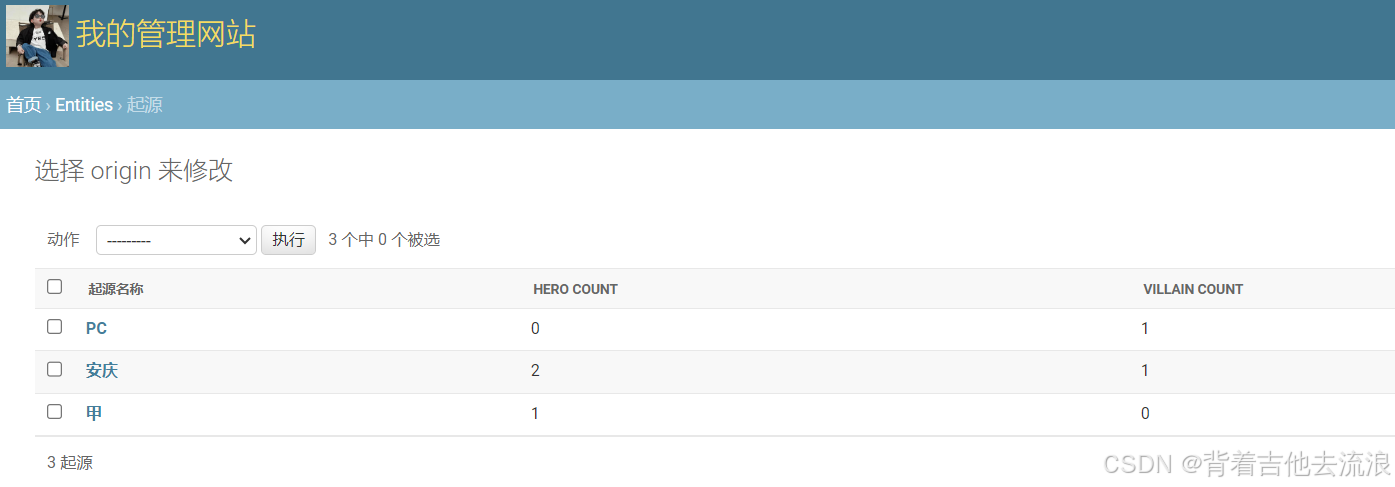
如果你的Admin后台中有很多计算字段,那么你需要对每个对象运行多个查询,这会使你的Admin后台变得非常慢。要解决此问题,你可以重写管理模型中的get_queryset方法使用annotate聚合函数来计算相关的字段。 以下示例为Origin模型的中ModelAdmin…...
—二分法》)
数据结构基础之《(3)—二分法》
一、认识二分法 1、经常见到的类型是在一个有序数组上,开展二分搜索 2、但有序真的是所有问题求解时使用二分的必要条件吗?不 3、只要能正确构建左右两侧的淘汰逻辑,你就可以二分 二、二分法怎么用 1、在一个有序数组中,找某个…...
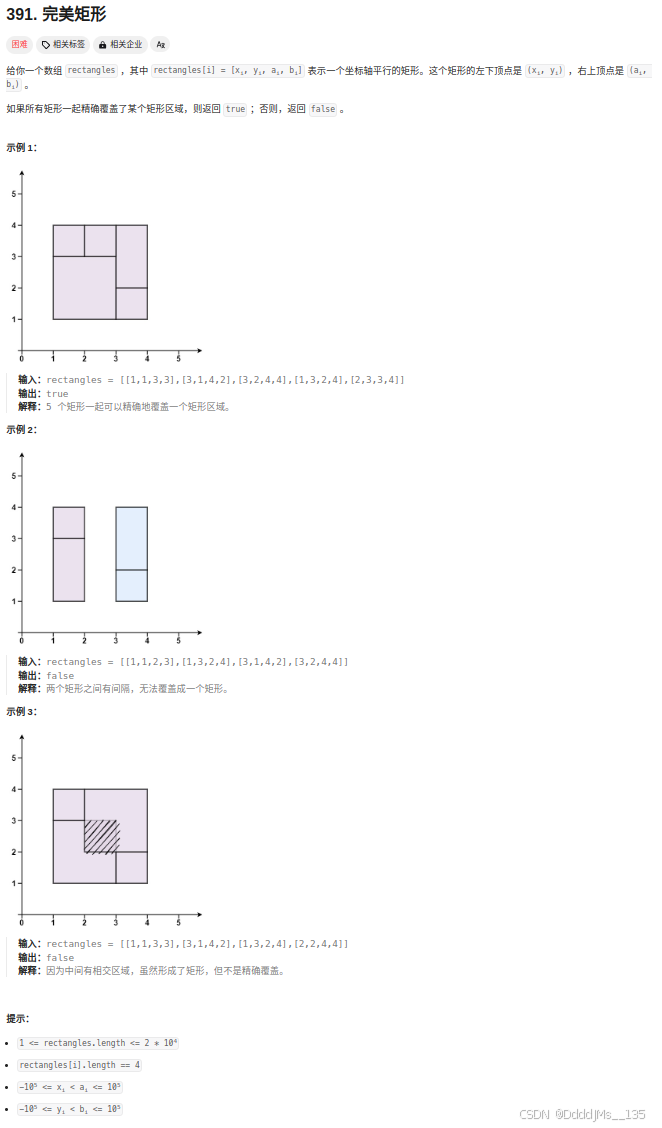
C语言 | Leetcode C语言题解之第391题完美矩形
题目: 题解: bool isSubsequence(char* s, char* t) {int mstrlen(s); int nstrlen(t);int k0; int j0;if(mn&&m0) return true;for(int i0;i<n;i){if(s[j]t[i]){j;}if(jm) return true;}return false; }...
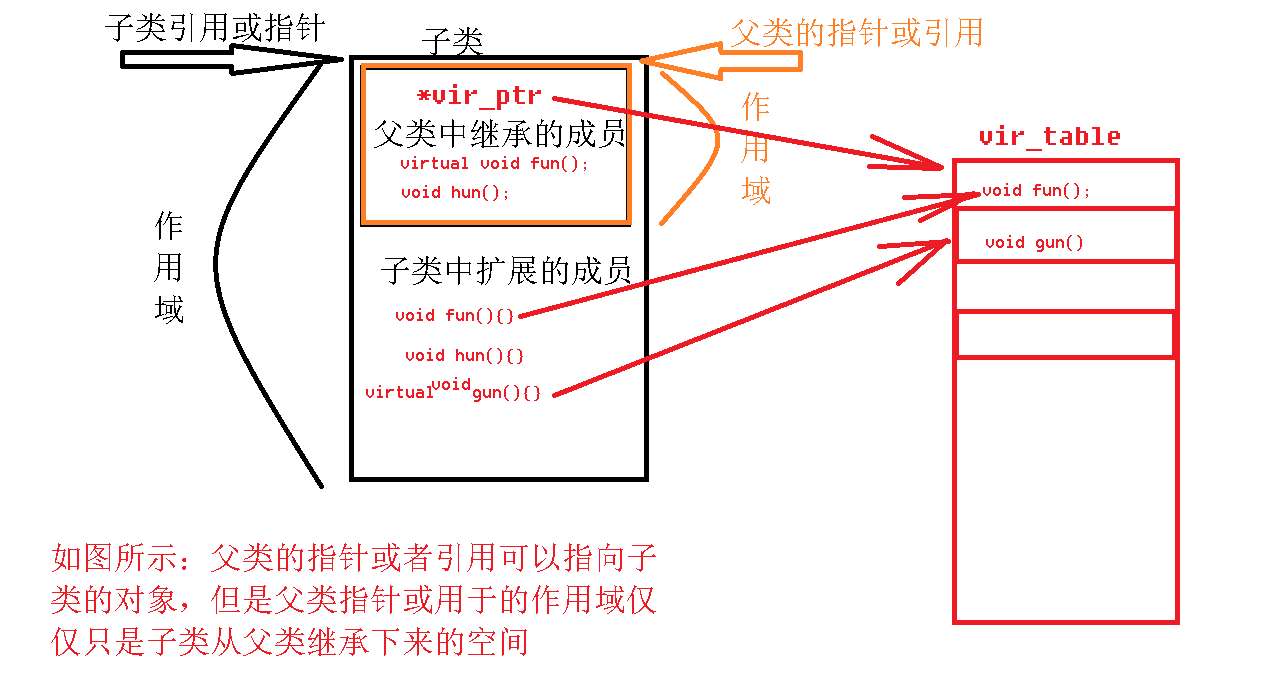
day47——面向对象特征之继承
一、继承(inhert) 面向对象三大特征:封装、继承、多态 继承:所谓继承,是类与类之间的关系。就是基于一个已有的类,来创建出一个新类的过程叫做继承。主要提高代码的复用性。 1.1 继承的作用 1> 实现…...

启动 Spring Boot 项目时指定特定的 application.yml 文件位置
java -jar your-spring-boot-app.jar --spring.config.locationfile:/path/to/your/config/application.yml your-spring-boot-app.jar 是你的 Spring Boot 应用的 JAR 文件名。file:/path/to/your/config/application.yml 是配置文件的绝对路径。 如果你有多个配置文件&#…...
Hive 本地启动时报错 Persistence Manager has been closed
Hive 本地启动时报错 Persistence Manager has been closed 2024-09-07 17:21:45 ERROR RetryingHMSHandler:215 - Retrying HMSHandler after 2000 ms (attempt 2 of 10) with error: javax.jdo.JDOFatalUserException: Persistence Manager has been closedat org.datanucle…...

多模态在京东内容算法上的应用
多模态在京东内容算法上的应用 作者:京东零售技术 2024-09-04 北京 本文字数:5226 字 阅读完需:约 17 分钟 本文作者唐烨参与 DataFunsummit2024:推荐系统架构峰会,在专题【多模态推荐论坛】中分享了多模态算法在京…...

SSM+Ajax实现广告系统
文章目录 1.案例需求2.编程思路3.案例源码(这里只给出新增部分的Handler和ajax部分,需要详情的可以私信我)4.小结 1.案例需求 使用SSMAjax实现广告系统,包括登录、查询所有、搜索、新增、删除、修改等功能,具体实现的效果图如下:…...
---UI 结构及与service互动)
项目实战 ---- 商用落地视频搜索系统(6)---UI 结构及与service互动
目录 背景 技术问题 描述 Jinja2 概述 特性 问题解决手段 问题1 问题2 问题3 代码实现 前端代码 python代码 解释 页面展示 home 上传视频 搜索视频 背景 通过1-5 我们已经搭建好完整的后台功能,service,及准备与UI 交互的路由及接口。下面就是UI 部分的搭…...

双头BFS
牛客月赛100 D题,过了80%数据,调了一下午。。。烦死了。。。 还是没调试出来,别人的代码用5维的距离的更新有滞后性,要在遍历之前要去重。。。 #include<bits/stdc.h> using namespace std; const int N2e310; char g[N][…...

使用Spring Boot拦截器实现时间戳校验以防止接口被恶意刷
使用Spring Boot拦截器实现时间戳校验以防止接口被恶意刷 在开发Web应用程序时,接口被恶意刷请求(例如DDoS攻击或暴力破解)是一个常见的安全问题。为了提高接口的安全性,我们可以在服务端实现时间戳校验,以确保请求的…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...
