数据结构基础之《(3)—二分法》
一、认识二分法
1、经常见到的类型是在一个有序数组上,开展二分搜索
2、但有序真的是所有问题求解时使用二分的必要条件吗?不
3、只要能正确构建左右两侧的淘汰逻辑,你就可以二分
二、二分法怎么用
1、在一个有序数组中,找某个数是否存在
public static boolean exist(int[] sortedArr, int num) {if (sortedArr == null || sortedArr.length == 0) {return false;}int L = 0;int R = sortedArr.length - 1;int mid = 0;while (L < R) {// 左移就是乘以二,右移就是除以二的意思// L 10亿 R 18亿,mid是整数,会溢出// N / 2,一个数除2,就等于这个数二进制形式带符号右移一位 N >> 1mid = L + ((R - L) >> 1); // 等于mid = (L + R) / 2if (sortedArr[mid] == num) {return true;} else if (sortedArr[mid] > num) {R = mid - 1;} else {L = mid + 1;}}return sortedArr[L] == num;}2、在一个有序数组中,找>=某个数最左侧的位置
例子
12222222333333333344444444444
要找>=2最左侧的位置
// 在arr上,找满足>=value的最左位置public static int nearestIndex(int[] arr, int value) {int L = 0;int R = arr.length - 1;int index = -1; // 记录最左的对号while (L <= R) {int mid = L + ((R - L) >> 1);if (arr[mid] >= value) {index = mid;R = mid - 1;} else {L = mid + 1;}}return index;}3、在一个有序数组中,找<=某个数最右侧的位置
4、局部最小值问题
(1)0位置的数比1位置的数小,就是局部最小
(2)N位置的数比N-1位置的数小,就是局部最小
(3)i位置的数,既比i-1位置的数小,也比i+1位置的数小,就是局部最小
5、局部最小问题详解
arr无序数组,任意两个相邻的数都不相等,返回一个局部最小的位置
理解:把值连成一个线,总有高峰低谷
逻辑二分思想:
满足一个条件把另一侧全部排除掉的选项,就可以二分
public static int getLessIndex(int[] arr) {if (arr == null || arr.length == 0) {return -1; // no exist}if (arr.length == 1 || arr[0] < arr[1]) {return 0;}if (arr[arr.length - 1] < arr[arr.length - 2]) {return arr.length - 1;}int left = 1;int right = arr.length - 2;int mid = 0;while (left < right) {mid = (left + right) / 2;if (arr[mid] > arr[mid - 1]) {right = mid - 1;} else if (arr[mid] > arr[mid + 1]) {left = mid + 1;} else {return mid;}}return left;}三、二分法时间复杂度
1、二分法查找的时间复杂度是依赖于2的几次方,所以O是log2(N),以2为底可以直接写成logN
相关文章:
—二分法》)
数据结构基础之《(3)—二分法》
一、认识二分法 1、经常见到的类型是在一个有序数组上,开展二分搜索 2、但有序真的是所有问题求解时使用二分的必要条件吗?不 3、只要能正确构建左右两侧的淘汰逻辑,你就可以二分 二、二分法怎么用 1、在一个有序数组中,找某个…...
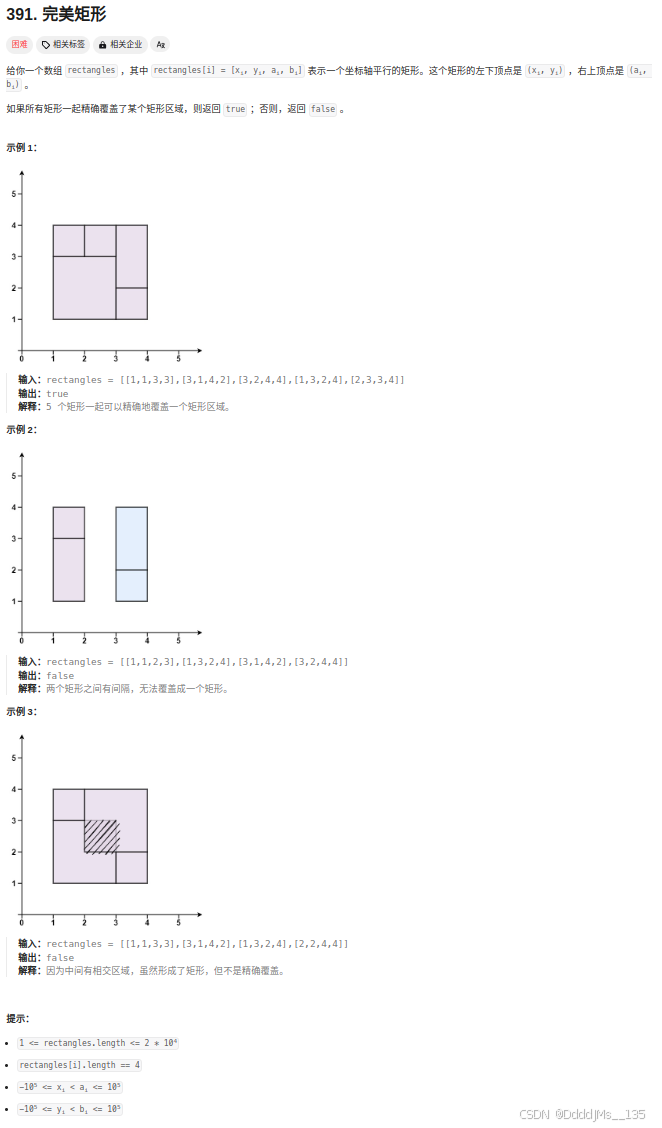
C语言 | Leetcode C语言题解之第391题完美矩形
题目: 题解: bool isSubsequence(char* s, char* t) {int mstrlen(s); int nstrlen(t);int k0; int j0;if(mn&&m0) return true;for(int i0;i<n;i){if(s[j]t[i]){j;}if(jm) return true;}return false; }...
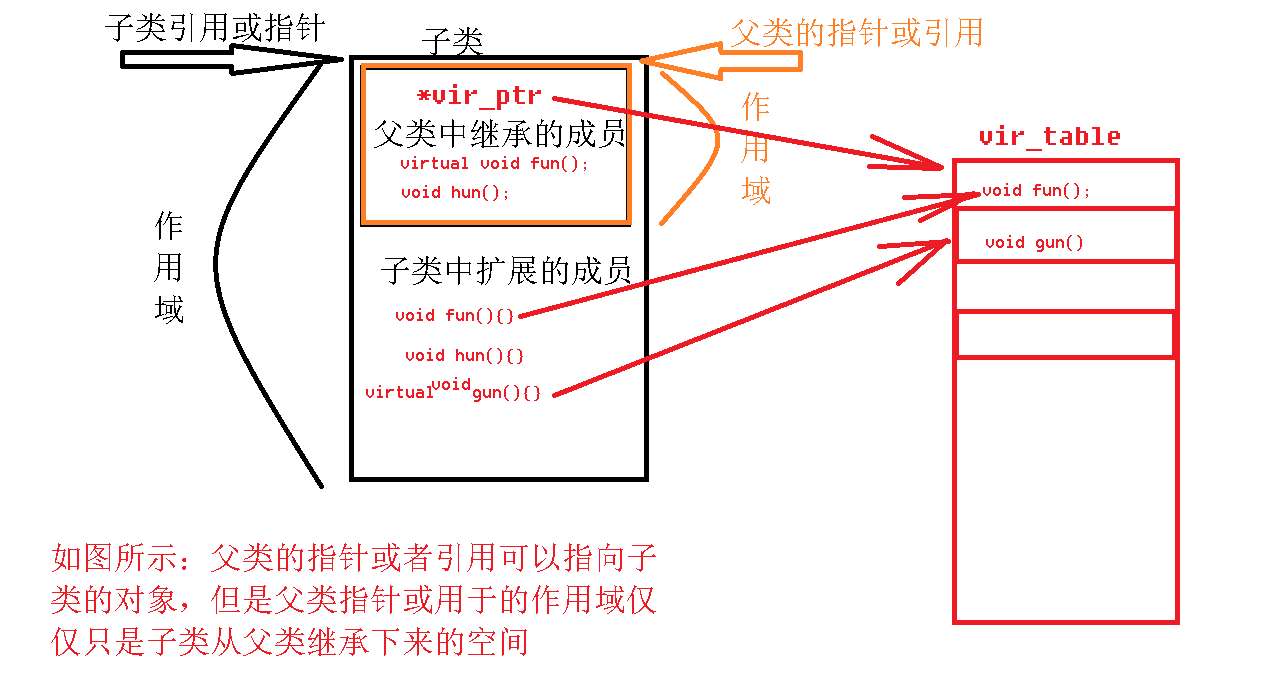
day47——面向对象特征之继承
一、继承(inhert) 面向对象三大特征:封装、继承、多态 继承:所谓继承,是类与类之间的关系。就是基于一个已有的类,来创建出一个新类的过程叫做继承。主要提高代码的复用性。 1.1 继承的作用 1> 实现…...

启动 Spring Boot 项目时指定特定的 application.yml 文件位置
java -jar your-spring-boot-app.jar --spring.config.locationfile:/path/to/your/config/application.yml your-spring-boot-app.jar 是你的 Spring Boot 应用的 JAR 文件名。file:/path/to/your/config/application.yml 是配置文件的绝对路径。 如果你有多个配置文件&#…...
Hive 本地启动时报错 Persistence Manager has been closed
Hive 本地启动时报错 Persistence Manager has been closed 2024-09-07 17:21:45 ERROR RetryingHMSHandler:215 - Retrying HMSHandler after 2000 ms (attempt 2 of 10) with error: javax.jdo.JDOFatalUserException: Persistence Manager has been closedat org.datanucle…...

多模态在京东内容算法上的应用
多模态在京东内容算法上的应用 作者:京东零售技术 2024-09-04 北京 本文字数:5226 字 阅读完需:约 17 分钟 本文作者唐烨参与 DataFunsummit2024:推荐系统架构峰会,在专题【多模态推荐论坛】中分享了多模态算法在京…...

SSM+Ajax实现广告系统
文章目录 1.案例需求2.编程思路3.案例源码(这里只给出新增部分的Handler和ajax部分,需要详情的可以私信我)4.小结 1.案例需求 使用SSMAjax实现广告系统,包括登录、查询所有、搜索、新增、删除、修改等功能,具体实现的效果图如下:…...
---UI 结构及与service互动)
项目实战 ---- 商用落地视频搜索系统(6)---UI 结构及与service互动
目录 背景 技术问题 描述 Jinja2 概述 特性 问题解决手段 问题1 问题2 问题3 代码实现 前端代码 python代码 解释 页面展示 home 上传视频 搜索视频 背景 通过1-5 我们已经搭建好完整的后台功能,service,及准备与UI 交互的路由及接口。下面就是UI 部分的搭…...

双头BFS
牛客月赛100 D题,过了80%数据,调了一下午。。。烦死了。。。 还是没调试出来,别人的代码用5维的距离的更新有滞后性,要在遍历之前要去重。。。 #include<bits/stdc.h> using namespace std; const int N2e310; char g[N][…...

使用Spring Boot拦截器实现时间戳校验以防止接口被恶意刷
使用Spring Boot拦截器实现时间戳校验以防止接口被恶意刷 在开发Web应用程序时,接口被恶意刷请求(例如DDoS攻击或暴力破解)是一个常见的安全问题。为了提高接口的安全性,我们可以在服务端实现时间戳校验,以确保请求的…...
第10讲 后端2
主要目标:理解滑动窗口法、位姿图优化、带IMU紧耦合的优化、掌握g2o位姿图。 第9讲介绍了以为BA为主的图优化。BA能精确优化每个相机位姿与特征点位置。不过在更大的场景中,大量特征点的存在会严重降低计算效率,导致计算量越来越大࿰…...

统计学习方法与实战——统计学习方法概论
统计学习方法概论 文章目录 统计学习方法概论前言章节目录导读 实现统计学习方法的步骤统计学习方法三要素模型模型是什么? 策略损失函数与风险函数常用损失函数ERM与SRM 算法 模型评估与模型选择过拟合与模型选择 正则化与交叉验证泛化能力生成模型与判别模型生成方法判别方法…...

人体红外传感器简介
人体红外传感器的工作原理是利用热释电效应,将人体发出的特定波长的红外线转化为电信号,从而实现对人体的检测和感知。 具体来说,人体红外传感器主要由滤光片、热释电探测元和前置放大器组成。滤光片的作用是使特定波长的红外辐…...

【JAVA入门】Day35 - 方法引用
【JAVA入门】Day35 - 方法引用 文章目录 【JAVA入门】Day35 - 方法引用一、方法引用的分类1.引用静态方法2.引用成员方法2.1 引用其他类的成员方法2.2 引用本类和父类的成员方法2.3 引用构造方法2.4 使用类名引用成员方法2.5 引用数组的构造方法 二、方法引用的例题 方法引用就…...
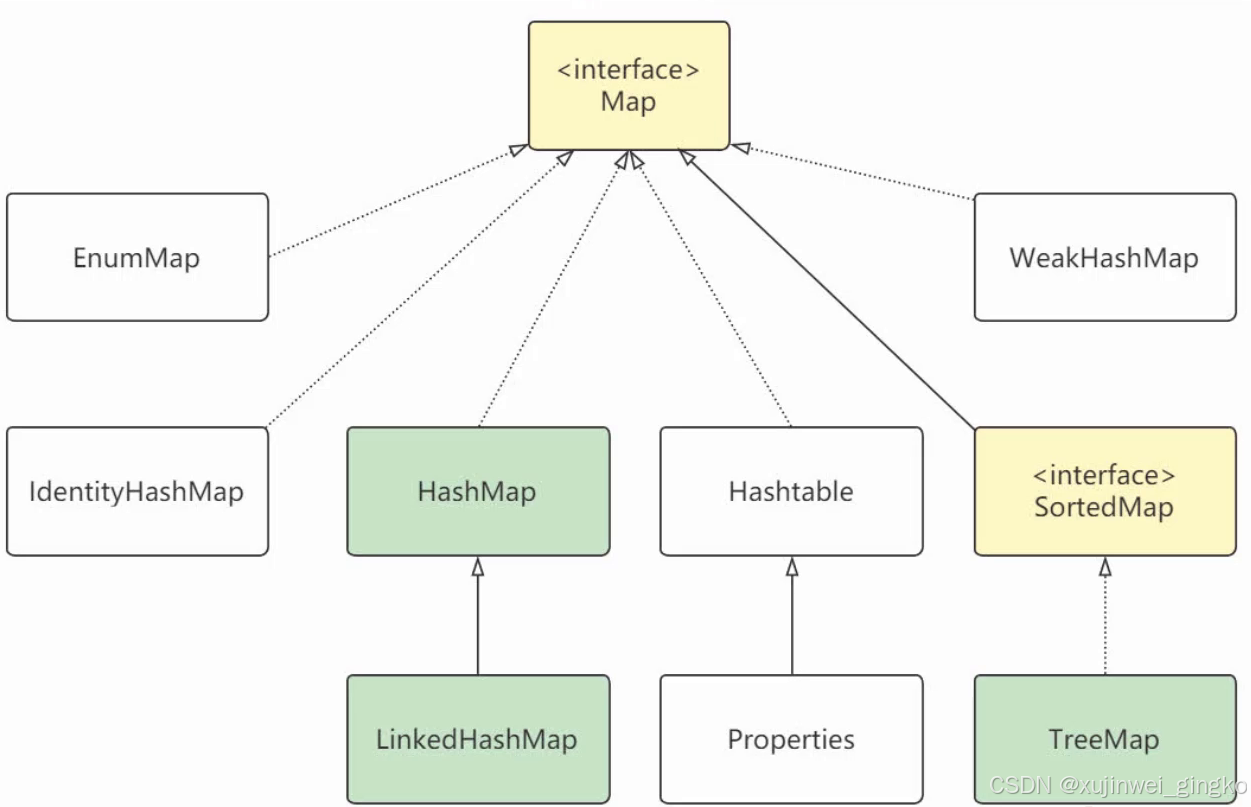
集合及映射
1、集合类图 1)ArrayList与LinkedList 区别 LinkedList 实现了双向队列的接口,对于数据的插入速度较快,只需要修改前后的指向即可;ArrayList对于特定位置插入数据,需要移动特定位置后面的数据,有额外开销 …...

软考基础知识之计算机网络
目录 前言 网络架构与协议 网络互联模型 1、OSI/RM 各层的功能 2、TCP/IP 结构模型 常见的网络协议 1、应用层协议 2、传输层协议 3、网络层协议 IPv6 前言 从古代的驿站、 八百里快马, 到近代的电报、 电话, 人类对于通信的追求从未间断&…...

云手机怎样简化海外社媒平台运营
随着越来越多的卖家希望拓展海外市场,运营TikTok、Facebook等社交媒体平台已经成为吸引流量和促进销售的重要手段。然而,在管理海外社媒账号的过程中,许多人会面临网络连接的问题。这时,使用一款高效便捷的云手机工具就显得尤为便…...

创业者必读!选择拍卖源码还是自建开发,哪种方案更安全?
在当今数字化时代,拍卖平台作为一种独特的电子商务模式,正逐渐成为人们关注的焦点。随着互联网技术的发展,网络安全问题变得越来越突出。如何保障用户数据安全,防止信息泄露及攻击事件的发生,已经成为拍卖软件开发者面…...

Spring Cloud Gateway整合基于STOMP协议的WebSocket实战及遇到问题解决
本实例介绍了Spring Cloud Gateway整合基于STOMP协议的WebSocket的实现。开发了聊天功能,和用户在线状态。解决了协议gateway整合websocket出现的问题 技术点 Spring Cloud GatewayNacosWebSocketSTOMPWebSocket与STOMP协议详解 1. WebSocket WebSocket 是一种通信协议,提…...

软考高级:系统架构设计师——软件架构设计 Chapter 笔记
软考高级:系统架构设计师——软件架构设计 1 软件架构设计—基本概念架构所处的位置架构发展历程架构的“41”视图例题 架构描述语言(ADL)例题 2软件架构设计—架构风格数据流风格调用/返回 风格独立构件风格虚拟机风格仓库风格(以…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
