统计学习方法与实战——统计学习方法概论
统计学习方法概论
文章目录
- 统计学习方法概论
- 前言
- 章节目录
- 导读
- 实现统计学习方法的步骤
- 统计学习方法三要素
- 模型
- 模型是什么?
- 策略
- 损失函数与风险函数
- 常用损失函数
- ERM与SRM
- 算法
- 模型评估与模型选择
- 过拟合与模型选择
- 正则化与交叉验证
- 泛化能力
- 生成模型与判别模型
- 生成方法
- 判别方法
- 分类问题、标注问题、回归问题
- 1. 分类问题
- 2. 标注问题(序列标注问题)
- 3. 回归问题
- 总结
前言
章节目录
- 统计学习
- 监督学习
- 基本概念
- 问题的形式化
- 统计学习三要素
- 模型
- 策略
- 算法
- 模型评估与模型选择
- 训练误差与测试误差
- 过拟合与模型选择
- 正则化与交叉验证
- 正则化
- 交叉验证
- 泛化能力
- 泛化误差
- 泛化误差上界
- 生成模型与判别模型
- 分类问题
- 标注问题
- 回归问题
导读
- 统计学习三要素对理解统计学习方法起到提纲挈领的作用
- 主要讨论监督学习
- 分类问题、标注问题和回归问题都是监督学习的重要问题
- 本书中介绍的统计学习方法包括…。这些方法是主要的分类、标注以及回归方法。他们又可归类为生成方法与判别方法。
-
输入和输出对称为样本
-
注意在介绍输入空间,输出空间等概念的时候,以及这一章的很多部分都会有个帽子,
监督学习中,监督学习可以概括如下:从给定有限的训练数据出发,假设数据是独立同分布的,而且假设模型属于某个假设空间,应用某一评价准则,从假设空间中选取一个最优的模型,使它对已给的训练数据以及未知测试数据在给定评价标准意义下有最准确的预测。,理解下这里的假设。
实现统计学习方法的步骤
统计学习方法三要素:模型,策略,算法
- 得到一个有限的训练数据集合
- 确定包含所有可能的模型的假设空间,即学习模型的集合
- 确定模型选择的准则,即学习的策略
- 实现求解最优模型的算法,即学习的算法
- 通过学习方法选择最优的模型
- 利用学习的最优模型对新数据进行预测或分析
统计学习方法三要素
模型
模型是什么?
在监督学习过程中,模型就是所要学习的条件概率分布或者决策函数。
策略
损失函数与风险函数
损失函数度量模型一次预测的好坏,风险函数度量平均意义下模型预测的好坏。
损失函数:衡量模型的推理结果与我们实际标签的差距
-
损失函数(loss function)或代价函数(cost function)
损失函数定义为给定输入 X X X的预测值 f ( X ) f(X) f(X)和真实值 Y Y Y之间的非负实值函数,记作 L ( Y , f ( X ) ) L(Y,f(X)) L(Y,f(X)) -
风险函数(risk function)或期望损失(expected loss)
这个和模型的泛化误差的形式是一样的
R e x p ( f ) = E p [ L ( Y , f ( X ) ) ] = ∫ X × Y L ( y , f ( x ) ) P ( x , y ) d x d y R_{exp}(f)=E_p[L(Y, f(X))]=\int_{\mathcal X\times\mathcal Y}L(y,f(x))P(x,y)\, {\rm d}x{\rm d}y Rexp(f)=Ep[L(Y,f(X))]=∫X×YL(y,f(x))P(x,y)dxdy
模型 f ( X ) f(X) f(X)关于联合分布 P ( X , Y ) P(X,Y) P(X,Y)的平均意义下的损失(期望损失),但是因为 P ( X , Y ) P(X,Y) P(X,Y)是未知的,所以前面的用词是期望,以及平均意义下的。这个表示其实就是损失的均值,反映了对整个数据的预测效果的好坏,P(x,y)转换成 ν ( X = x , Y = y ) N \frac {\nu(X=x, Y=y)}{N} Nν(X=x,Y=y)更容易直观理解, 但是真实的数据N是无穷的。
-
经验风险(empirical risk)或经验损失(empirical loss)
R e m p ( f ) = 1 N ∑ i = 1 N L ( y i , f ( x i ) ) R_{emp}(f)=\frac{1}{N}\sum^{N}_{i=1}L(y_i,f(x_i)) Remp(f)=N1∑i=1NL(yi,f(xi))
模型 f f f关于训练样本集的平均mean损失
根据大数定律,当样本容量N趋于无穷大时,经验风险趋于期望风险 -
结构风险(structural risk)
R s r m ( f ) = 1 N ∑ i = 1 N L ( y i , f ( x i ) ) + λ J ( f ) R_{srm}(f)=\frac{1}{N}\sum_{i=1}^{N}L(y_i,f(x_i))+\lambda J(f) Rsrm(f)=N1∑i=1NL(yi,f(xi))+λJ(f)
J ( f ) J(f) J(f)为模型复杂度, λ ⩾ 0 \lambda \geqslant 0 λ⩾0是系数,用以权衡经验风险和模型复杂度。
常用损失函数
损失函数数值越小,模型就越好
L ( Y , f ( X ) ) L(Y,f(X)) L(Y,f(X))
- 0-1损失
L = { 1 , Y ≠ f ( X ) 0 , Y = f ( X ) L=\begin{cases}1, Y \neq f(X) \\0, Y=f(X) \end{cases} L={1,Y=f(X)0,Y=f(X) - 平方损失,张量之差的平方
L = ( Y − f ( X ) ) 2 L=(Y-f(X))^2 L=(Y−f(X))2 - 绝对损失,两个值直接相减
L = ∣ Y − f ( X ) ∣ L=|Y-f(X)| L=∣Y−f(X)∣
L ( Y , P ( Y ∣ X ) ) L(Y,P(Y|X)) L(Y,P(Y∣X))
- 对数损失
这里 P ( Y ∣ X ) ⩽ 1 P(Y|X)\leqslant 1 P(Y∣X)⩽1,对应的对数是负值,所以对数损失中包含一个负号,为什么不是绝对值?因为肯定是负的。
L = − log P ( Y ∣ X ) L=-\log P(Y|X) L=−logP(Y∣X)
ERM与SRM
经验风险最小化(ERM)与结构风险最小化(SRM)
- 极大似然估计是经验风险最小化的一个例子
当模型是条件概率分布,损失函数是对数损失函数时,经验风险最小化等价于极大似然估计 - 贝叶斯估计中的最大后验概率估计是结构风险最小化的一个例子
当模型是条件概率分布,损失函数是对数损失函数,模型复杂度由模型的先验概率表示时,结构风险最小化等价于最大后验概率估计
算法
模型评估与模型选择
训练误差和测试误差是模型关于数据集的平均损失。
统计学习方法具体采用的损失函数未必是评估时使用的损失函数`,这句理解下。参考下在数据科学比赛中给出的评分标准,与实际学习采用的损失函数之间的关系。
- 训练时使用的损失函数与测试时的损失函数不一定一样
过拟合与模型选择
这部分讲到了最小二乘法,举例:
这个问题中训练数据为 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\{(x_1, y_1),(x_2,y_2),\cdots,(x_N,y_N)\} T={(x1,y1),(x2,y2),⋯,(xN,yN)}
模型为
f M ( x , w ) = w 0 + w 1 x + w 2 x 2 + ⋯ + w M x M = ∑ j = 0 M w j x j f_M(x,w)=w_0+w_1x+w_2x^2+\cdots+w_Mx^M=\sum\limits_{j=0}^Mw_jx^j fM(x,w)=w0+w1x+w2x2+⋯+wMxM=j=0∑Mwjxj
经验风险最小化策略下
L ( w ) = 1 2 ∑ i = 1 N ( f ( x i , w ) − y i ) 2 L(w)=\frac{1}{2}\sum\limits_{i=1}^N(f(x_i,w)-y_i)^2 L(w)=21i=1∑N(f(xi,w)−yi)2
将模型和训练数据带入到上式得到
L ( w ) = 1 2 ∑ i = 1 N ( ∑ j = 0 M w j x i j − y i ) 2 = 1 2 ∑ i = 1 N ( w ⋅ x i − y i ) 2 L(w)=\frac{1}{2}\sum\limits_{i=1}^N\left(\sum\limits_{j=0}^Mw_jx_i^j-y_i\right)^2=\frac{1}{2}\sum\limits_{i=1}^N(w\cdot x_i-y_i)^2 L(w)=21i=1∑N(j=0∑Mwjxij−yi)2=21i=1∑N(w⋅xi−yi)2
这个问题要求 w = ( w 0 ∗ , w 1 ∗ , ⋯ , w M ∗ ) w=(w_0^*,w_1^*,\cdots,w_M^*) w=(w0∗,w1∗,⋯,wM∗)
对 w w w求偏导令其为零,得到一系列方程,求解可以用梯度下降或者矩阵分解。
求解线性方程组 A x = b Ax=b Ax=b,可以表示为 x = A / b x=A/b x=A/b,问题展开之后可以涉及到矩阵分解。
TODO: 这个例子展开一下
正则化与交叉验证
- 正则化
模型选择的典型方法是正则化 - 交叉验证
另一种常用的模型选择方法是交叉验证- 简单
- S折(K折, K-Fold)[^1]
- 留一法
泛化能力
-
现实中采用最多的方法是通过测试误差来评价学习方法的泛化能力
-
统计学习理论试图从理论上对学习方法的泛化能力进行分析
-
学习方法的泛化能力往往是通过研究泛化误差的概率上界进行的, 简称为泛化误差上界(generalization error bound)
注意泛化误差的定义,书中有说事实上,泛化误差就是所学习到的模型的期望风险
生成模型与判别模型
监督学习方法可分为生成方法(generative approach)与判别方法(discriminative approach)
生成方法
generative approach
- 可以还原出联合概率分布 P ( X , Y ) P(X,Y) P(X,Y)
- 收敛速度快, 当样本容量增加时, 学到的模型可以更快收敛到真实模型
- 当存在隐变量时仍可以用
判别方法
discriminative approach
- 直接学习条件概率 P ( Y ∣ X ) P(Y|X) P(Y∣X)或者决策函数 f ( X ) f(X) f(X)
- 直接面对预测, 往往学习准确率更高
- 可以对数据进行各种程度的抽象, 定义特征并使用特征, 可以简化学习问题
分类问题、标注问题、回归问题
Classification, Tagging, Regression
- 分类系统和标注系统的差异外,没看到其他差异,但实际上这两幅图中对应的输入数据有差异,序列数据的 x i = ( x i ( 1 ) , x i ( 2 ) , … , x i ( n ) ) T x_i = (x_i^{(1)},x_i^{(2)},\dots,x_i^{(n)})^T xi=(xi(1),xi(2),…,xi(n))T对应了
- 回归问题的产出为 Y = f ^ ( X ) Y=\hat f(X) Y=f^(X)
分类和回归其实都是相对而说,分类模型其实也可以用于回归,只是用于任务的不同
在机器学习和深度学习中,问题通常可以分为几种类型,包括分类问题、标注问题和回归问题。以下是对这三种问题的详细解释:
1. 分类问题
定义:分类问题是指将输入数据分配到预定义的类别或标签中。目标是根据输入特征预测离散的输出类别。
特点:
- 输出是离散的,通常是有限个类别。
- 常见的评估指标包括准确率、精确率、召回率和F1-score等。
示例:
- 二分类问题:例如,判断一封电子邮件是否为垃圾邮件(是/否)。
- 多分类问题:例如,识别图像中的物体(如猫、狗、鸟等)。
应用:
- 图像分类(如手写数字识别、物体检测)
- 文本分类(如情感分析、主题分类)
- 医疗诊断(如疾病分类)
2. 标注问题(序列标注问题)
定义:标注问题是指对输入序列中的每个元素进行标注,通常用于处理序列数据。目标是为每个输入元素分配一个标签。
特点:
- 输入是一个序列,输出是与输入序列长度相同的标签序列。
- 常见的评估指标包括准确率、F1-score等。
示例:
- 命名实体识别(NER):在文本中识别出人名、地名、组织名等。
- 词性标注:为句子中的每个单词分配词性标签(如名词、动词、形容词等)。
- 语音识别:将语音信号转换为文本,并为每个音素或词分配标签。
应用:
- 自然语言处理(如文本分析、信息提取)
- 生物信息学(如基因序列标注)
- 计算机视觉(如图像分割)
3. 回归问题
定义:回归问题是指预测一个连续的数值输出。目标是根据输入特征预测一个实数值。
特点:
- 输出是连续的,可以是任意实数。
- 常见的评估指标包括均方误差(MSE)、均绝对误差(MAE)和R²(决定系数)等。
示例:
- 预测房价:根据房屋的特征(如面积、位置、卧室数量等)预测其市场价格。
- 股票价格预测:根据历史数据预测未来的股票价格。
- 温度预测:根据气象数据预测未来的温度。
应用:
- 财务预测(如销售额、利润预测)
- 经济学(如GDP预测)
- 工程(如材料强度预测)
总结
- 分类问题:将输入分配到离散类别中,输出是类别标签。
- 标注问题:对输入序列中的每个元素进行标注,输出是与输入序列长度相同的标签序列。
- 回归问题:预测连续的数值输出,输出是实数值。
这三种问题在机器学习中有着广泛的应用,选择合适的模型和算法来解决这些问题是机器学习实践中的关键。
相关文章:

统计学习方法与实战——统计学习方法概论
统计学习方法概论 文章目录 统计学习方法概论前言章节目录导读 实现统计学习方法的步骤统计学习方法三要素模型模型是什么? 策略损失函数与风险函数常用损失函数ERM与SRM 算法 模型评估与模型选择过拟合与模型选择 正则化与交叉验证泛化能力生成模型与判别模型生成方法判别方法…...

人体红外传感器简介
人体红外传感器的工作原理是利用热释电效应,将人体发出的特定波长的红外线转化为电信号,从而实现对人体的检测和感知。 具体来说,人体红外传感器主要由滤光片、热释电探测元和前置放大器组成。滤光片的作用是使特定波长的红外辐…...

【JAVA入门】Day35 - 方法引用
【JAVA入门】Day35 - 方法引用 文章目录 【JAVA入门】Day35 - 方法引用一、方法引用的分类1.引用静态方法2.引用成员方法2.1 引用其他类的成员方法2.2 引用本类和父类的成员方法2.3 引用构造方法2.4 使用类名引用成员方法2.5 引用数组的构造方法 二、方法引用的例题 方法引用就…...
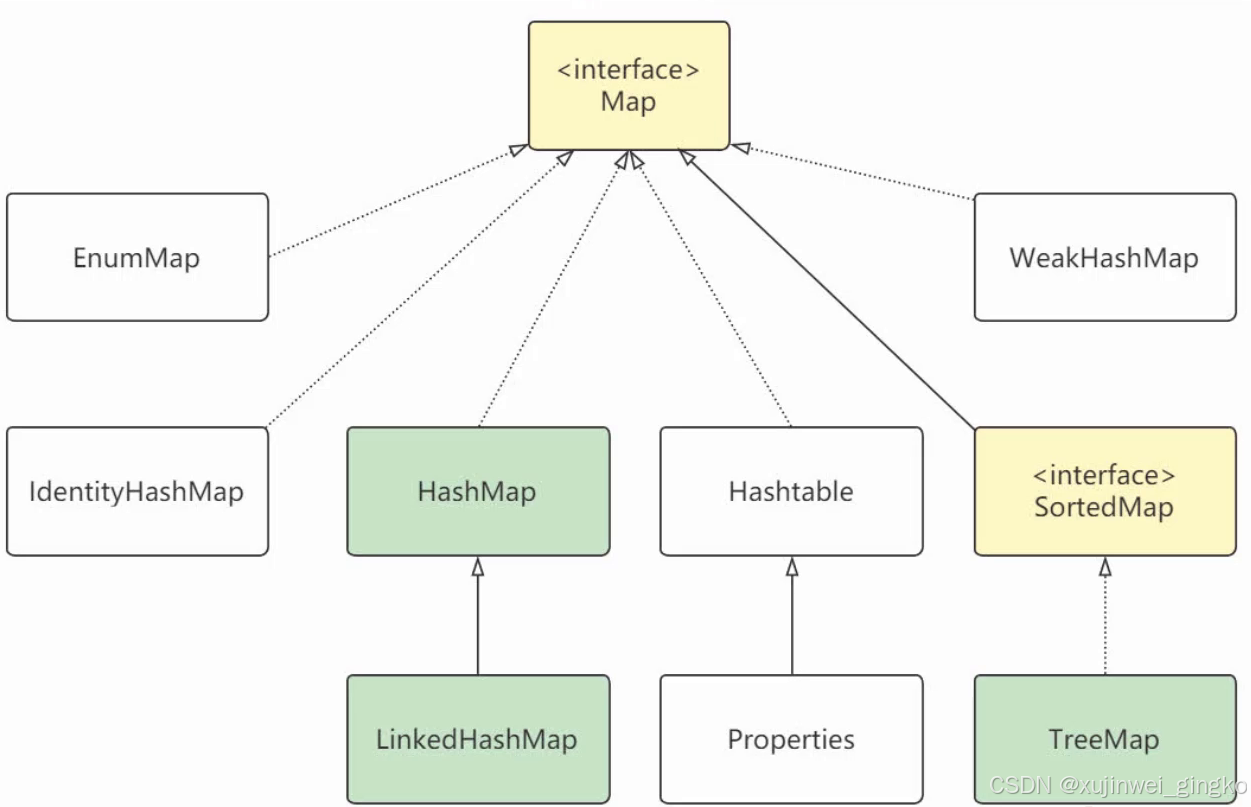
集合及映射
1、集合类图 1)ArrayList与LinkedList 区别 LinkedList 实现了双向队列的接口,对于数据的插入速度较快,只需要修改前后的指向即可;ArrayList对于特定位置插入数据,需要移动特定位置后面的数据,有额外开销 …...

软考基础知识之计算机网络
目录 前言 网络架构与协议 网络互联模型 1、OSI/RM 各层的功能 2、TCP/IP 结构模型 常见的网络协议 1、应用层协议 2、传输层协议 3、网络层协议 IPv6 前言 从古代的驿站、 八百里快马, 到近代的电报、 电话, 人类对于通信的追求从未间断&…...

云手机怎样简化海外社媒平台运营
随着越来越多的卖家希望拓展海外市场,运营TikTok、Facebook等社交媒体平台已经成为吸引流量和促进销售的重要手段。然而,在管理海外社媒账号的过程中,许多人会面临网络连接的问题。这时,使用一款高效便捷的云手机工具就显得尤为便…...

创业者必读!选择拍卖源码还是自建开发,哪种方案更安全?
在当今数字化时代,拍卖平台作为一种独特的电子商务模式,正逐渐成为人们关注的焦点。随着互联网技术的发展,网络安全问题变得越来越突出。如何保障用户数据安全,防止信息泄露及攻击事件的发生,已经成为拍卖软件开发者面…...

Spring Cloud Gateway整合基于STOMP协议的WebSocket实战及遇到问题解决
本实例介绍了Spring Cloud Gateway整合基于STOMP协议的WebSocket的实现。开发了聊天功能,和用户在线状态。解决了协议gateway整合websocket出现的问题 技术点 Spring Cloud GatewayNacosWebSocketSTOMPWebSocket与STOMP协议详解 1. WebSocket WebSocket 是一种通信协议,提…...

软考高级:系统架构设计师——软件架构设计 Chapter 笔记
软考高级:系统架构设计师——软件架构设计 1 软件架构设计—基本概念架构所处的位置架构发展历程架构的“41”视图例题 架构描述语言(ADL)例题 2软件架构设计—架构风格数据流风格调用/返回 风格独立构件风格虚拟机风格仓库风格(以…...

PageHelper组件 实现前端分页查询功能
Hi~!这里是一颗小谷粒,很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~~💥💥个人主页:一颗小谷粒💥💥所属专栏:Web前端开发 💥💥博主…...

线性回归与逻辑回归在模型参数优化上的比较
概述 线性回归和逻辑回归是两种基础且广泛应用的预测模型。尽管它们在很多方面有相似之处,如都使用梯度下降算法来优化模型参数,但在优化目标和方法上存在一些关键差异。本文将探讨这两种模型在参数优化上的差异,并提供相应的代码示例。 线…...

JavaWeb JavaScript 10.日程管理 第一期
自我消耗,敏感是我, 明媚是我, 我横跳在不同的情绪中 —— 24.8.31 一、登录页及校验 1.校验账号格式 // 校验账号格式function checkUsername(){// 定义正则表达式表示字符串规则var usernameReg /^[a-zA-Z0-9]{5,10}$/;// 获取用户名输入…...

redis为什么快
春内存访问,相比数据库访问磁盘要快单线程,避免上下文切换带来的cpu开销渐进式Rehash。减少阻塞网络模型多路复用,reactor模型 常用基本数据类型 5个基本数据类型2个高级数据结构(bitmaps、hyperlog) redis高级功能…...
 部署SpringBoot3.0)
十分钟学会Kubernetes(K8S) 部署SpringBoot3.0
1、十分钟学会Kubernetes(K8S) 部署SpringBoot3.0 本课程以 Java 后端开发的视角,带着大家从零基础入门 k8s 实战,掌握企业级容器化管理平台的各种实战应用,以及 Prometheus 监控告警、ELK 日志收集、DevOps 等众多实战课程内容,大…...

顺序表的插入与删除
一.插入:插入前先移动后面的元素 1.图解: 在b和d之间插入c,此时就需要把d,e,f都向后移一位,腾出一个位置后插入c。 2.代码实现: #include<stdio.h> #define MaxSize 10 //定义最大长度…...

FFMPEG -- 音频开发
1:前言 在进行音频开发之前需要先知道一些基础知识,一些有必要的指导的概念。 1.1 声音的产生、获取和转换 声音的产生的本质是靠震动,声音的传播需要借助媒介,比如空气、液体、固体等媒介。在自然界中声音的可视化为音波的形式&…...
翻译)
lxml官方入门教程(The lxml.etree Tutorial)翻译
lxml官方入门教程(The lxml.etree Tutorial)翻译 说明: 首次发表日期:2024-09-05官方教程链接: https://lxml.de/tutorial.html使用KIMI和豆包机翻水平有限,如有错误请不吝指出 这是一个关于使用lxml.et…...

string详解
Golang详解string 文章目录 Golang详解stringGolang中为什么string是只读的?stirng和[]byte的转化原理[]byte转string一定需要内存拷贝吗?字符串拼接性能测试 Golang中为什么string是只读的? 在Go语言中,string其实就是一个结构体…...

基于约束大于规范的想法,封装缓存组件
架构?何谓架构?好像并没有一个准确的概念。以前我觉得架构就是搭出一套完美的框架,可以让其他开发人员减少不必要的代码开发量;可以完美地实现高内聚低耦合的准则;可以尽可能地实现用最少的硬件资源,实现最高的程序效率…...

自动化测试面试真题(附答案)
一、编程语法题 1 、 python 有哪些数据类型 python 数据类型有很多,基本数据类型有整型(数字)、字符串、元组、列表、字典和布尔类型等 2 、怎么将两个字典合并 调用字典的 update 方法,合并 2 个字典。 3 、 json.l python …...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...
