顺序表的插入与删除
一.插入:插入前先移动后面的元素
1.图解:

在b和d之间插入c,此时就需要把d,e,f都向后移一位,腾出一个位置后插入c。
2.代码实现:
#include<stdio.h>
#define MaxSize 10 //定义最大长度typedef struct
{int data[MaxSize]; //用静态的"数组"存放数据元素int length; //顺序表的当前长度
}SqList; //顺序表的类型定义
//基本操作 - 初始化一个顺序表
void InitList(SqList &L)
{for(int i=0;i<MaxSize;i++){L.data[i]=0; //将所有数据元素设置为默认初始值 }L.length=0; //顺序表初始长度为0 ,因为一开始没存元素
}
//插入
void ListInsert(SqList &L,int i,int e) //i必须在1到Length+1上才有效,/*比如长度为5,要加在第6个位置上,往后移动一个位置就长度为6,此时可添加在第6个位置上,如果仍长度为5,要加在第7个位置上,往后移动一个位置就长度为6,没有第7个位置,添加失败*///元素存满时也不能继续插入数据
{for(int j=L.length ; j>=i ; j--) //将第i个元素及之后的元素后移 {L.data[j]=L.data[j-1];}L.data[i-1]=e; //在位置i处放入eL.length++; //长度加1,因为多了一个元素
}
int main()
{SqList L; //声明一个顺序表InitList(L); //初始化顺序表//...此处省略一些代码,插入几个元素ListInsert(L,3,3); return 0;
}
/*位序从1开始,数组索引从0开始 */ 
代码优化:
#include<stdio.h>
#include<stdbool.h>
#define MaxSize 10 //定义最大长度typedef struct
{int data[MaxSize]; //用静态的"数组"存放数据元素int length; //顺序表的当前长度
}SqList; //顺序表的类型定义
//基本操作 - 初始化一个顺序表
void InitList(SqList &L)
{for(int i=0;i<MaxSize;i++){L.data[i]=0; //将所有数据元素设置为默认初始值 }L.length=0; //顺序表初始长度为0 ,因为一开始没存元素
}
//插入
bool ListInsert(SqList &L,int i,int e) //i必须在1到Length+1上才有效,/*比如长度为5,要加在第6个位置上,往后移动一个位置就长度为6,此时可添加在第6个位置上,如果仍长度为5,要加在第7个位置上,往后移动一个位置就长度为6,没有第7个位置,添加失败*///元素存满时也不能继续插入数据
{if(i<1||i>L.length+1) //判断i的范围是否有效 {return false;}if(L.length>=MaxSize) //判断当前存储空间是否已满,以决定能否继续插入 {return false;}//走到这儿说明能插入数据 for(int j=L.length ; j>=i ; j--) //将第i个元素及之后的元素后移 {L.data[j]=L.data[j-1];}L.data[i-1]=e; //在位置i处放入eL.length++; //长度加1,因为多了一个元素 return true;
}
int main()
{SqList L; //声明一个顺序表InitList(L); //初始化顺序表//...此处省略一些代码,插入几个元素ListInsert(L,3,3); return 0;
}
/*位序从1开始,数组索引从0开始 */ 
3.时间复杂度:
问题规模n=L.length(表长),当添加一个元素后,长度为n+1,
所以在第一个位置添加元素时,要把前n个元素后移,空出第一个位置,此时长度为n+1。

二.删除:删除后先移动前面的元素
1.图解:

删除c后,后面的d,e,f都要前移一个,数组长度减一。


2.代码实现:
#include<stdio.h>
#include<stdbool.h>
#define MaxSize 10 //定义最大长度
typedef struct
{int data[MaxSize]; //用静态的"数组"存放数据元素int length; //顺序表的当前长度
}SqList; //顺序表的类型定义
//基本操作 - 初始化一个顺序表
void InitList(SqList &L)
{for(int i=0;i<MaxSize;i++){L.data[i]=0; //将所有数据元素设置为默认初始值 }L.length=0; //顺序表初始长度为0 ,因为一开始没存元素
}
//删除
bool ListDelete(SqList &L,int i,int &e)
/*参数&L:代表要删除的顺序表;参数i:代表要删除的第i个元素;参数&e:代表把删除的元素返回*/
{if(i<1||i>L.length) //判断i的范围是否有效 (判断语句为或:全假才假->才不走if;只要有一个是真就是真->就走if)//本例i为3,L.length为0,所以i>L.length为真,走if {return false;}//走到这儿说明i有效,能删除数据e=L.data[i-1]; //将被删除的元素赋值给efor(int j=i;j<L.length;j++) //将第i个位置后的元素前移 {L.data[j-1]=L.data[j];} L.length--; //线性表长度减一return true;
}
int main()
{SqList L; //声明一个顺序表InitList(L); //初始化顺序表//...此处省略一些代码,插入几个元素int e=-1; //用变量e把删除的元素"带回来"if( ListDelete(L,3,e) ){printf("已删除第3个元素,删除的元素的值为=%d \n",e);}else{printf("位序i不合法,删除失败 \n");} return 0;
}ListDelete第三个参数有个&,这样就使得main函数里的e和ListDelete函数里的e是同一个e,
不加&,main函数里的e和ListDelete函数里的e就不是同一个e了,执行完ListDelete函数后,main函数里的e的值没发生改变。
3.时间复杂度:

例如i为2时,剩下n-2个,然后剩下的n-2个依次循环。
三.总结:

相关文章:

顺序表的插入与删除
一.插入:插入前先移动后面的元素 1.图解: 在b和d之间插入c,此时就需要把d,e,f都向后移一位,腾出一个位置后插入c。 2.代码实现: #include<stdio.h> #define MaxSize 10 //定义最大长度…...

FFMPEG -- 音频开发
1:前言 在进行音频开发之前需要先知道一些基础知识,一些有必要的指导的概念。 1.1 声音的产生、获取和转换 声音的产生的本质是靠震动,声音的传播需要借助媒介,比如空气、液体、固体等媒介。在自然界中声音的可视化为音波的形式&…...
翻译)
lxml官方入门教程(The lxml.etree Tutorial)翻译
lxml官方入门教程(The lxml.etree Tutorial)翻译 说明: 首次发表日期:2024-09-05官方教程链接: https://lxml.de/tutorial.html使用KIMI和豆包机翻水平有限,如有错误请不吝指出 这是一个关于使用lxml.et…...

string详解
Golang详解string 文章目录 Golang详解stringGolang中为什么string是只读的?stirng和[]byte的转化原理[]byte转string一定需要内存拷贝吗?字符串拼接性能测试 Golang中为什么string是只读的? 在Go语言中,string其实就是一个结构体…...

基于约束大于规范的想法,封装缓存组件
架构?何谓架构?好像并没有一个准确的概念。以前我觉得架构就是搭出一套完美的框架,可以让其他开发人员减少不必要的代码开发量;可以完美地实现高内聚低耦合的准则;可以尽可能地实现用最少的硬件资源,实现最高的程序效率…...

自动化测试面试真题(附答案)
一、编程语法题 1 、 python 有哪些数据类型 python 数据类型有很多,基本数据类型有整型(数字)、字符串、元组、列表、字典和布尔类型等 2 、怎么将两个字典合并 调用字典的 update 方法,合并 2 个字典。 3 、 json.l python …...

云原生架构概念
云原生架构概念 云原生架构(Cloud Native Architechtrue)作为一种现代软件开发的革新力量,正在逐渐改变企业构建、部署和管理应用程序的方式。它的核心优势在于支持微服务架构,使得应用程序能够分解为独立、松耦合的服务…...

85、 探针
一、pod的进阶 pod的进阶: 1.1、pod的生命周期当中的状态: 1、Running运行中,pod已经分配到节点上且pod内的容器正常运行。正常状态(ready 1/1)。 2、complete:完成之后退出,容器内的返回码…...
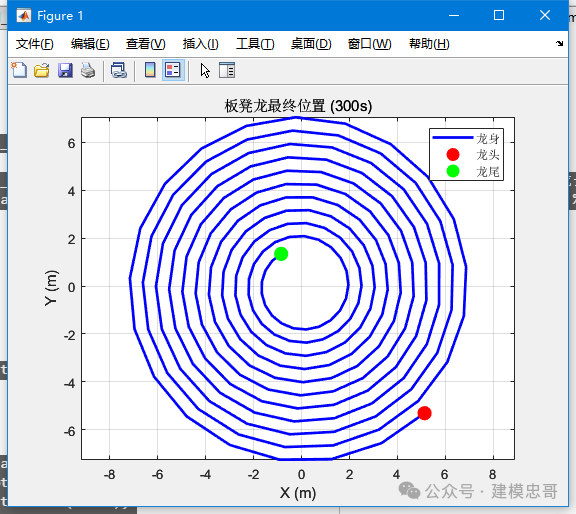
2024全国大学省数学建模竞赛A题-原创参考论文(部分+第一问代码)
一问题重述 1.1 问题背景 "板凳龙",又称"盘龙",是浙闽地区的传统地方民俗文化活动。这种独特的表演艺术形式融合了中国传统龙舞的精髓和地方特色,展现了人们对美好生活的向往和对传统文化的传承。 在板凳龙表演中&am…...

在VScode上写网页(html)
一、首先点进VScode,下载3个插件。 VScode安装:VScode 教程 | 菜鸟教程 二、新建 HTML 文件 作者运行的代码来自:http://t.csdnimg.cn/vIAQi 把代码复制粘贴进去,然后点击文件→另存为→选择html格式。 三、运行代码...

C#中LINQ的Cast<T>与OfType<T>
在C#中,Cast() 方法是LINQ(Language Integrated Query)的一部分,它位于 System.Linq 命名空间中。这个方法用于将 IEnumerable 集合(或任何实现了 IEnumerable 接口的集合)的元素转换为指定类型 T 的集合。…...

小阿轩yx-Kubernertes日志收集
小阿轩yx-Kubernertes日志收集 前言 在 Kubernetes 集群中如何通过不同的技术栈收集容器的日志,包括程序直接输出到控制台日志、自定义文件日志等 有哪些日志需要收集 日志收集与分析很重要,为了更加方便的处理异常 简单总结一些比较重要的需要收集…...

0to1使用Redis实现“登录验证”次数限制
1 引言 系统为了避免密码遭到暴力破解,通常情况下需要在登录时,限制用户验证账号密码的次数,当达到一定的验证次数后,在一段时间内锁定该账号,不再验证。本章将用几行代码实现该功能,完整代码链接在文章最…...

ARM----时钟
时钟频率可以是由晶振提供的,我们需要高频率,但是外部接高的晶振会不稳定,所有使用PLL(锁相环)来放大频率。接下来就让我们学习用外部晶振提供的频率来配置时钟频率。 一.时钟源的选择 在这里我们选择外部晶振作为时钟…...

NISP 一级 —— 考证笔记合集
该笔记为导航目录,在接下来一段事件内,我会每天发布我关于考取该证书的相关笔记。 当更新完成后,此条注释会被删除。 第一章 信息安全概述 1.1 信息与信息安全1.2 信息安全威胁1.3 信息安全发展阶段与形式1.4 信息安全保障1.5 信息系统安全保…...

C++三位状态比较排序
数组相同元素个数及按序 void 交换3个数升(int& A, int& B, int& C, bool& k) {int J 0;if (B > A&&A > C)J C, C B, B A, A J, k true;//231else if (C > A&&A > B)J A, A B, B J, k true;//213else if (A > B&a…...

麒麟系统安装GPU驱动
1.nvidia 1.1显卡驱动 本机显卡型号:nvidia rtx 3090 1.1.1下载驱动 打开 https://www.nvidia.cn/geforce/drivers/ 也可以直接使用下面这个地址下载 https://www.nvidia.com/download/driverResults.aspx/205464/en-us/ 1.1.3安装驱动 右击,为run文件添加可…...

IDEA 安装lombok插件不兼容的问题及解决方法
解决:IDEA 安装lombok插件不兼容问题,plugin xxxx is incompatible 一、去官网下载最新的2024版本 地址传送通道: lombok插件官网地址https://plugins.jetbrains.com/plugin/6317-lombok/versions/stable 二、修改参数的配置 在压缩包路径…...

聊聊说话的习惯
1 在日常生活中,每个人都有固定的说话习惯。心理学研究表明,通过一个人的说话习惯,也可以分析出他的性格特点。对于每一个人来讲,说话习惯已经融为他们生活中的一部分。在社交活动中,一些不良的说话习惯很可能会给他们带来麻烦。…...

当水泵遇上物联网:智能水务新时代的浪漫交响
在当代科技的宏伟乐章中,物联网(IoT)技术宛如一位技艺高超的指挥家,引领着各行各业迈向智能化的新纪元。当这股创新浪潮涌向古老的水务行业时,一场前所未有的“智能水务”革命便悄然上演,而水泵——这一传统…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
