线性回归与逻辑回归在模型参数优化上的比较
概述
线性回归和逻辑回归是两种基础且广泛应用的预测模型。尽管它们在很多方面有相似之处,如都使用梯度下降算法来优化模型参数,但在优化目标和方法上存在一些关键差异。本文将探讨这两种模型在参数优化上的差异,并提供相应的代码示例。
线性回归的参数优化
线性回归的目标是找到一组参数,使得预测值与实际值之间的均方误差最小。其优化目标是损失函数,即均方误差(MSE)。
损失函数
线性回归的损失函数定义为:
[ J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y{(i)})2 ]
其中,( h_\theta(x) = \theta^T x )是模型的预测函数,( m )是样本数量,( \theta )是模型参数。
梯度下降
为了最小化损失函数,线性回归使用梯度下降算法来更新参数:
[ \theta := \theta - \alpha \cdot \nabla_\theta J(\theta) ]
梯度计算如下:
[ \nabla_\theta J(\theta) = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) x^{(i)} ]
代码示例
以下是使用Python的scikit-learn库实现线性回归的示例代码:
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error# 示例数据
X = np.array([[1], [2], [3], [4]])
y = np.array([2, 4, 6, 8])# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建线性回归模型
lin_reg = LinearRegression()# 训练模型
lin_reg.fit(X_train, y_train)# 预测测试集
y_pred = lin_reg.predict(X_test)# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse:.2f}")
逻辑回归的参数优化
逻辑回归的目标是找到一组参数,使得模型能够正确分类样本。其优化目标是损失函数,即交叉熵损失。
损失函数
逻辑回归的损失函数定义为:
[ J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} [y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)}))] ]
其中,( h_\theta(x) = \frac{1}{1 + e{-\thetaT x}} )是模型的预测函数,( m )是样本数量,( \theta )是模型参数。
梯度下降
为了最小化损失函数,逻辑回归同样使用梯度下降算法来更新参数:
[ \theta := \theta - \alpha \cdot \nabla_\theta J(\theta) ]
梯度计算如下:
[ \nabla_\theta J(\theta) = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) x^{(i)} ]
代码示例
以下是使用Python的scikit-learn库实现逻辑回归的示例代码:
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 示例数据
X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]])
y = np.array([0, 0, 1, 1])# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建逻辑回归模型
log_reg = LogisticRegression()# 训练模型
log_reg.fit(X_train, y_train)# 预测测试集
y_pred = log_reg.predict(X_test)# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"Accuracy: {accuracy:.2f}")
比较
优化目标
- 线性回归:优化目标是最小化预测值与实际值之间的均方误差。
- 逻辑回归:优化目标是最小化模型预测概率与实际标签之间的交叉熵损失。
梯度计算
- 线性回归:梯度是预测值与实际值之差的线性组合。
- 逻辑回归:梯度是预测概率与实际标签之差的线性组合。
应用场景
- 线性回归:适用于预测连续数值,如房价、温度等。
- 逻辑回归:适用于二分类问题,如垃圾邮件检测、疾病诊断等。
结论
线性回归和逻辑回归在模型参数优化上的主要差异在于它们的优化目标和梯度计算方式。线性回归通过最小化均方误差来预测连续数值,而逻辑回归通过最小化交叉熵损失来进行分类。理解这些差异有助于我们选择合适的模型和优化策略,以解决特定的预测问题。通过掌握这两种回归模型的参数优化方法,我们可以更有效地应用机器学习算法解决实际问题。
✅作者简介:热爱科研的人工智能开发者,修心和技术同步精进
❤欢迎关注我的知乎:对error视而不见
代码获取、问题探讨及文章转载可私信。
☁ 愿你的生命中有够多的云翳,来造就一个美丽的黄昏。
🍎获取更多人工智能资料可点击链接进群领取,谢谢支持!👇
点击领取更多详细资料
相关文章:

线性回归与逻辑回归在模型参数优化上的比较
概述 线性回归和逻辑回归是两种基础且广泛应用的预测模型。尽管它们在很多方面有相似之处,如都使用梯度下降算法来优化模型参数,但在优化目标和方法上存在一些关键差异。本文将探讨这两种模型在参数优化上的差异,并提供相应的代码示例。 线…...

JavaWeb JavaScript 10.日程管理 第一期
自我消耗,敏感是我, 明媚是我, 我横跳在不同的情绪中 —— 24.8.31 一、登录页及校验 1.校验账号格式 // 校验账号格式function checkUsername(){// 定义正则表达式表示字符串规则var usernameReg /^[a-zA-Z0-9]{5,10}$/;// 获取用户名输入…...

redis为什么快
春内存访问,相比数据库访问磁盘要快单线程,避免上下文切换带来的cpu开销渐进式Rehash。减少阻塞网络模型多路复用,reactor模型 常用基本数据类型 5个基本数据类型2个高级数据结构(bitmaps、hyperlog) redis高级功能…...
 部署SpringBoot3.0)
十分钟学会Kubernetes(K8S) 部署SpringBoot3.0
1、十分钟学会Kubernetes(K8S) 部署SpringBoot3.0 本课程以 Java 后端开发的视角,带着大家从零基础入门 k8s 实战,掌握企业级容器化管理平台的各种实战应用,以及 Prometheus 监控告警、ELK 日志收集、DevOps 等众多实战课程内容,大…...

顺序表的插入与删除
一.插入:插入前先移动后面的元素 1.图解: 在b和d之间插入c,此时就需要把d,e,f都向后移一位,腾出一个位置后插入c。 2.代码实现: #include<stdio.h> #define MaxSize 10 //定义最大长度…...

FFMPEG -- 音频开发
1:前言 在进行音频开发之前需要先知道一些基础知识,一些有必要的指导的概念。 1.1 声音的产生、获取和转换 声音的产生的本质是靠震动,声音的传播需要借助媒介,比如空气、液体、固体等媒介。在自然界中声音的可视化为音波的形式&…...
翻译)
lxml官方入门教程(The lxml.etree Tutorial)翻译
lxml官方入门教程(The lxml.etree Tutorial)翻译 说明: 首次发表日期:2024-09-05官方教程链接: https://lxml.de/tutorial.html使用KIMI和豆包机翻水平有限,如有错误请不吝指出 这是一个关于使用lxml.et…...

string详解
Golang详解string 文章目录 Golang详解stringGolang中为什么string是只读的?stirng和[]byte的转化原理[]byte转string一定需要内存拷贝吗?字符串拼接性能测试 Golang中为什么string是只读的? 在Go语言中,string其实就是一个结构体…...

基于约束大于规范的想法,封装缓存组件
架构?何谓架构?好像并没有一个准确的概念。以前我觉得架构就是搭出一套完美的框架,可以让其他开发人员减少不必要的代码开发量;可以完美地实现高内聚低耦合的准则;可以尽可能地实现用最少的硬件资源,实现最高的程序效率…...

自动化测试面试真题(附答案)
一、编程语法题 1 、 python 有哪些数据类型 python 数据类型有很多,基本数据类型有整型(数字)、字符串、元组、列表、字典和布尔类型等 2 、怎么将两个字典合并 调用字典的 update 方法,合并 2 个字典。 3 、 json.l python …...

云原生架构概念
云原生架构概念 云原生架构(Cloud Native Architechtrue)作为一种现代软件开发的革新力量,正在逐渐改变企业构建、部署和管理应用程序的方式。它的核心优势在于支持微服务架构,使得应用程序能够分解为独立、松耦合的服务…...

85、 探针
一、pod的进阶 pod的进阶: 1.1、pod的生命周期当中的状态: 1、Running运行中,pod已经分配到节点上且pod内的容器正常运行。正常状态(ready 1/1)。 2、complete:完成之后退出,容器内的返回码…...
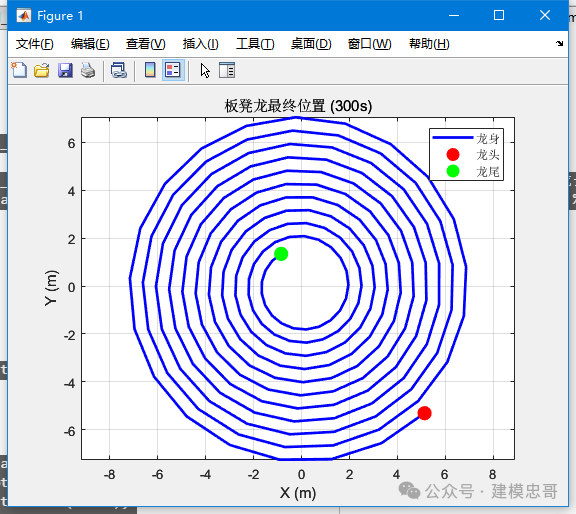
2024全国大学省数学建模竞赛A题-原创参考论文(部分+第一问代码)
一问题重述 1.1 问题背景 "板凳龙",又称"盘龙",是浙闽地区的传统地方民俗文化活动。这种独特的表演艺术形式融合了中国传统龙舞的精髓和地方特色,展现了人们对美好生活的向往和对传统文化的传承。 在板凳龙表演中&am…...

在VScode上写网页(html)
一、首先点进VScode,下载3个插件。 VScode安装:VScode 教程 | 菜鸟教程 二、新建 HTML 文件 作者运行的代码来自:http://t.csdnimg.cn/vIAQi 把代码复制粘贴进去,然后点击文件→另存为→选择html格式。 三、运行代码...

C#中LINQ的Cast<T>与OfType<T>
在C#中,Cast() 方法是LINQ(Language Integrated Query)的一部分,它位于 System.Linq 命名空间中。这个方法用于将 IEnumerable 集合(或任何实现了 IEnumerable 接口的集合)的元素转换为指定类型 T 的集合。…...

小阿轩yx-Kubernertes日志收集
小阿轩yx-Kubernertes日志收集 前言 在 Kubernetes 集群中如何通过不同的技术栈收集容器的日志,包括程序直接输出到控制台日志、自定义文件日志等 有哪些日志需要收集 日志收集与分析很重要,为了更加方便的处理异常 简单总结一些比较重要的需要收集…...

0to1使用Redis实现“登录验证”次数限制
1 引言 系统为了避免密码遭到暴力破解,通常情况下需要在登录时,限制用户验证账号密码的次数,当达到一定的验证次数后,在一段时间内锁定该账号,不再验证。本章将用几行代码实现该功能,完整代码链接在文章最…...

ARM----时钟
时钟频率可以是由晶振提供的,我们需要高频率,但是外部接高的晶振会不稳定,所有使用PLL(锁相环)来放大频率。接下来就让我们学习用外部晶振提供的频率来配置时钟频率。 一.时钟源的选择 在这里我们选择外部晶振作为时钟…...

NISP 一级 —— 考证笔记合集
该笔记为导航目录,在接下来一段事件内,我会每天发布我关于考取该证书的相关笔记。 当更新完成后,此条注释会被删除。 第一章 信息安全概述 1.1 信息与信息安全1.2 信息安全威胁1.3 信息安全发展阶段与形式1.4 信息安全保障1.5 信息系统安全保…...

C++三位状态比较排序
数组相同元素个数及按序 void 交换3个数升(int& A, int& B, int& C, bool& k) {int J 0;if (B > A&&A > C)J C, C B, B A, A J, k true;//231else if (C > A&&A > B)J A, A B, B J, k true;//213else if (A > B&a…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...
