python科学计算:NumPy 线性代数与矩阵操作
1 NumPy 中的矩阵与数组
在 NumPy 中,矩阵实际上是一种特殊的二维数组,因此几乎所有数组的操作都可以应用到矩阵上。不过,矩阵运算与一般的数组运算存在一定的区别,尤其是在点积、乘法等操作中。
1.1 创建矩阵
矩阵可以通过 NumPy 的 array() 函数创建。矩阵的形状可以通过 shape 属性来访问。
import numpy as np# 创建一个 2x3 矩阵
matrix = np.array([[1, 2, 3], [4, 5, 6]])print("矩阵:\n", matrix)
print("矩阵的形状:", matrix.shape)
1.2 矩阵与标量的运算
矩阵与标量的加法、减法、乘法和除法等运算会作用于矩阵的每个元素,类似于数组的广播机制。
# 矩阵与标量的运算
result = matrix * 2
print("矩阵与标量相乘的结果:\n", result)
2 矩阵的基本运算
2.1 矩阵加法与减法
矩阵加法和减法是元素对应的操作,只有当两个矩阵的形状相同时,才能进行加法或减法。
# 创建两个矩阵
matrix1 = np.array([[1, 2], [3, 4]])
matrix2 = np.array([[5, 6], [7, 8]])# 矩阵加法
sum_matrix = matrix1 + matrix2
print("矩阵加法结果:\n", sum_matrix)# 矩阵减法
diff_matrix = matrix1 - matrix2
print("矩阵减法结果:\n", diff_matrix)
2.2 矩阵乘法
NumPy 中的 dot() 函数用于执行矩阵乘法,或称为矩阵的点积操作。矩阵乘法的前提是第一个矩阵的列数必须等于第二个矩阵的行数。
# 矩阵乘法
product_matrix = np.dot(matrix1, matrix2)
print("矩阵乘法结果:\n", product_matrix)
注意: 矩阵的元素对应乘法使用
*操作符即可,但这不是矩阵乘法。
2.3 矩阵转置
transpose() 函数用于矩阵的转置操作,即将矩阵的行和列互换。
# 矩阵转置
transposed_matrix = matrix1.transpose()
print("转置后的矩阵:\n", transposed_matrix)
2.4 单位矩阵与对角矩阵
- 单位矩阵: 单位矩阵是主对角线元素全为 1,其余元素全为 0 的矩阵,可以使用
np.eye()创建。 - 对角矩阵: 对角矩阵是除了对角线外,其余元素均为 0 的矩阵,可以使用
np.diag()创建。
# 创建单位矩阵
identity_matrix = np.eye(3)
print("单位矩阵:\n", identity_matrix)# 创建对角矩阵
diag_matrix = np.diag([1, 2, 3])
print("对角矩阵:\n", diag_matrix)
3 矩阵的逆与行列式
3.1 矩阵的逆
可逆矩阵(即非奇异矩阵)是指其行列式不为 0 的矩阵。NumPy 提供了 inv() 函数用于计算矩阵的逆。只有方阵(行数等于列数的矩阵)才能求逆。
from numpy.linalg import inv# 计算矩阵的逆
inverse_matrix = inv(matrix1)
print("矩阵的逆:\n", inverse_matrix)
3.2 矩阵的行列式
矩阵的行列式是一个标量值,用来描述矩阵的某些性质。det() 函数用于计算方阵的行列式。如果矩阵的行列式为 0,则该矩阵不可逆。
from numpy.linalg import det# 计算矩阵的行列式
determinant = det(matrix1)
print("矩阵的行列式:", determinant)
4 特征值与特征向量
在线性代数中,特征值和特征向量是非常重要的概念。对于一个方阵,特征向量是非零向量,当该向量与矩阵相乘时,结果是原向量的一个倍数,该倍数称为特征值。
4.1 计算特征值和特征向量
eig() 函数可以用于计算方阵的特征值和特征向量。返回的结果是一个包含两个数组的元组:第一个数组是特征值,第二个数组是对应的特征向量。
from numpy.linalg import eig# 计算特征值与特征向量
eigenvalues, eigenvectors = eig(matrix1)
print("特征值:", eigenvalues)
print("特征向量:\n", eigenvectors)
4.2 特征值分解的应用
特征值分解在很多领域都有广泛的应用,例如主成分分析(PCA)、图像压缩等。通过特征值分解,可以将矩阵分解成多个简单的矩阵形式,简化后续计算。
5 奇异值分解(SVD)
奇异值分解(Singular Value Decomposition, SVD)是一种矩阵分解技术,用于将矩阵分解为三个矩阵的乘积。它在数据压缩、降维等领域非常有用。
5.1 svd() 函数
svd() 函数可以将矩阵分解为三个矩阵:U、S 和 V。其中 U 和 V 是正交矩阵,S 是一个对角矩阵。
from numpy.linalg import svd# 进行奇异值分解
U, S, V = svd(matrix1)
print("U 矩阵:\n", U)
print("S 矩阵:\n", S)
print("V 矩阵:\n", V)
5.2 SVD 的应用
SVD 被广泛应用于信号处理、图像压缩和数据降维等领域。例如,在推荐系统中,SVD 可用于分解用户-物品评分矩阵,从而提取出用户和物品的潜在特征。
6 矩阵的分解
除了奇异值分解,NumPy 还支持其他几种矩阵分解方法,比如 LU 分解和 QR 分解。
1 LU 分解
LU 分解将一个矩阵分解为一个下三角矩阵和一个上三角矩阵。NumPy 提供了 lu() 函数来进行 LU 分解。
from scipy.linalg import lu# LU 分解
P, L, U = lu(matrix1)
print("P 矩阵:\n", P)
print("L 矩阵:\n", L)
print("U 矩阵:\n", U)
2 QR 分解
QR 分解将矩阵分解为一个正交矩阵和一个上三角矩阵。NumPy 提供了 qr() 函数来进行 QR 分解。
# QR 分解
Q, R = np.linalg.qr(matrix1)
print("Q 矩阵:\n", Q)
print("R 矩阵:\n", R)
相关文章:

python科学计算:NumPy 线性代数与矩阵操作
1 NumPy 中的矩阵与数组 在 NumPy 中,矩阵实际上是一种特殊的二维数组,因此几乎所有数组的操作都可以应用到矩阵上。不过,矩阵运算与一般的数组运算存在一定的区别,尤其是在点积、乘法等操作中。 1.1 创建矩阵 矩阵可以通过 Nu…...

Unity面向对象补全计划 之 List<T>与class(非基础)
C# & Unity 面向对象补全计划 泛型-CSDN博客 关于List,其本质就是C#封装好的一个数组,是一个很好用的轮子,所以并不需要什么特别说明 问题描述 假设我们有一个表示学生的类 Student,每个学生有姓名和年龄两个属性。我们需要创…...

ant design vue+vue3+ts+xlsx实现表格导出问excel文件(带自定义表头)~
1、首先默认你已安装ant design vue、xlsx 库、及file-saver。 2、导入: import * as XLSX from xlsx; import { saveAs } from file-saver; 注:这里的xlsx导入不能这么写,否则会报错,原因是版本不一致,语法向上兼容…...
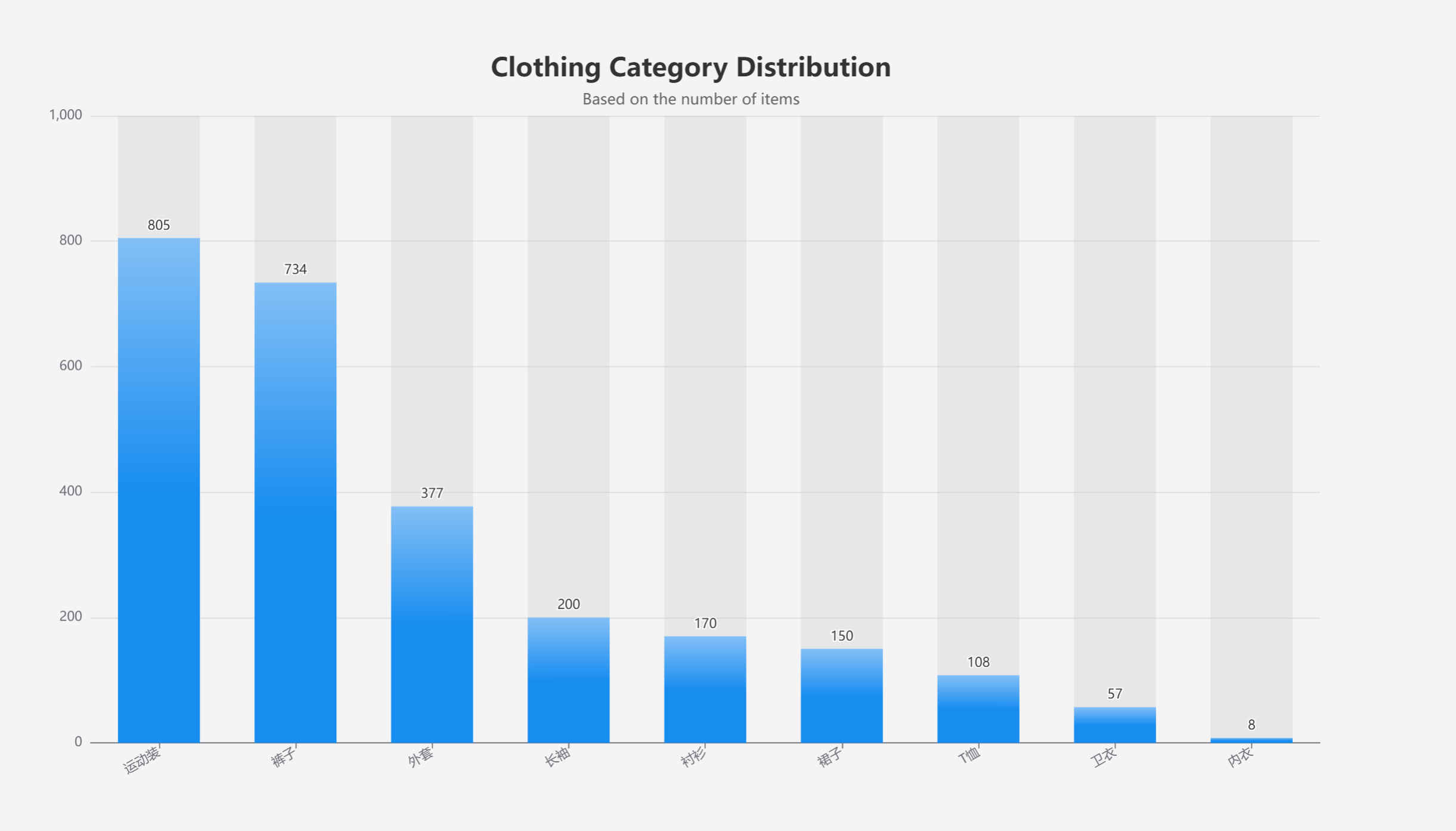
基于Python爬虫的淘宝服装数据分析项目
文章目录 一.项目介绍二.爬虫代码代码分析 三. 数据处理四. 数据可视化 一.项目介绍 该项目是基于Python爬虫的淘宝服装数据分析项目,以致于帮助商家了解当前服装市场的需求,制定更加精确的营销策略。首先,需要爬取淘宝中关于服装的大量数据…...

Tomcat控制台乱码问题已解决(2024/9/7
步骤很详细,直接上教程 问题复现: 情景一 情景二 原因简述 这是由于编码不一致引起的,Tomcat启动后默认编码UTF-8,而Windows的默认编码是GBK。因此你想让其不乱码,只需配置conf\logging.properties的编码格式即可 解决…...

vue通过html2canvas+jspdf生成PDF问题全解(水印,分页,截断,多页,黑屏,空白,附源码)
前端导出PDF的方法不多,常见的就是利用canvas画布渲染,再结合jspdf导出PDF文件,代码也不复杂,网上的代码基本都可以拿来即用。 如果不是特别追求完美的情况下,或者导出PDF内容单页的话,那么基本上也就满足业…...

服务器数据恢复—Raid磁盘阵列故障类型和常见故障原因
出于尽可能避免数据灾难的设计初衷,RAID解决了3个问题:容量问题、IO性能问题、存储安全(冗余)问题。从数据恢复的角度讨论RAID的存储安全问题。 常见的起到存储安全作用的RAID方案有RAID1、RAID5及其变形。基本设计思路是相似的:当部分数据异…...

C++字符串中的string类操作
愿我如星君如月,夜夜流光相皎洁。 ——《车逍遥篇》【宋】范成大 目录 正文: 主要特点: 基本操作: 代码演示: 总结: 今天我们接着上次的章节继续,这次我们来说一个为解决上个方法的缺陷而诞…...

axios设置responseType: ‘blob‘,获取接口返回的错误信息
在axios的请求中当后端接口返回的是文件流的情况下,我们需要在请求参数里面设置responseType: blob,如果接口报错,默认前端无法获取后端返回的错误信息。 解决方法:通过FileReader获取错误信息 async handleFetch() {const res aw…...

【C++】:模板初阶—函数模板|类模板
✨ Blog’s 主页: 白乐天_ξ( ✿>◡❛) 🌈 个人Motto:他强任他强,清风拂山岗! 💫 欢迎来到我的学习笔记! 本文参考博客:一同感受C模版的所带来的魅力 一、泛型编程思想 首先…...

Java 远程执行服务器上的命令
在Java中使用JSch库执行远程服务器上的命令是一种常见的做法,特别是在需要自动化运维任务或者进行远程文件操作时。以下是基于Codekru网站提供的示例,展示如何使用JSch库在远程服务器上执行单个或多个命令。 准备工作 首先,确保您的项目中已…...

3DMax基础- 创建基础模型
目录 零.软件简介 一. 标准基本型 长方体 圆锥体 球体 圆柱体 管状体 圆环 四棱锥 茶壶 平面编辑 加强型文本 二. 扩展基本体 三.复合对象 变形 散布 一致 连接 图形合并 布尔 并集 合并 交集 差集 四.门和窗 门 窗 植物,栏杆,墙 零.软件简介 3…...

JavaScript 知识点(从基础到进阶)
🌏个人博客主页:心.c 前言:JavaScript已经学完了,和大家分享一下我的笔记,希望大家可以有所收获,花不多说,开干!!! 🔥🔥ǵ…...

计算机网络知识点复习——TCP协议的三次握手与四次挥手(连接与释放)
TCP协议的三次握手与四次挥手(连接与释放) 一、前言二、简单的知识准备1. TCP协议的主要特点2. TCP报文段 三、TCP连接的建立(三次握手)四、TCP连接的释放(四次挥手)五、TCP连接与释放的总结六、结束语 一、…...

SpringDataJPA系列(7)Jackson注解在实体中应用
SpringDataJPA系列(7)Jackson注解在实体中应用 常用的Jackson注解 Springboot中默认集成的是Jackson,我们可以在jackson依赖包下看到Jackson有多个注解 一般常用的有下面这些: 一个实体的示例 测试方法如下: 按照上述图片中的序号做个简…...

【Spring Boot 3】【Web】统一封装 HTTP 响应体
【Spring Boot 3】【Web】统一封装 HTTP 响应体 背景介绍开发环境开发步骤及源码工程目录结构总结背景 软件开发是一门实践性科学,对大多数人来说,学习一种新技术不是一开始就去深究其原理,而是先从做出一个可工作的DEMO入手。但在我个人学习和工作经历中,每次学习新技术总…...

Linux如何做ssh反向代理
SSH反向代理是一种通过SSH协议实现的安全远程访问方式,它允许客户端通过SSH连接到一台具有公网IP的代理服务器,然后这台代理服务器再将请求转发给内部网络中的目标主机。以下是实现SSH反向代理的步骤: 一、准备工作 确保服务器配置ÿ…...

Verilog语法+:和-:有什么用?
Verilog语法:和-:主要用于位选择,可以让代码更简洁。 一、位选择基础 在Verilog中,位选择可以通过直接索引来实现,例如: reg [7:0] data; wire select_a; wire [2:0] select_b; assign select_a data[3]; assign select_b …...

stm32F103 串口2 中断 无法接收指定字符串 [已解决]
stm32F103 串口2中断接收指定字符串 USART 初始化和中断配置示例中断处理函数示例关键点总结 确保在串口配置中正确使能空闲中断 ( USART_IT_IDLE) 是关键。这个中断可以帮助你在串口接收一帧数据完成后,进行相应的处理和分析。 为了确保你在串口配置时能避免类似问…...

Matlab/Simulink和AMEsim联合仿真(以PSO-PID算法为例)
目录 安装软件和配置环境变量 Matlab/Simulink和AMEsim联合仿真详细流程 非常重要的一点 Simulink模型和AMEsim模型用S-Function建立连接 从AMEsim软件打开Matlab Matlab里的设置 Matlab的.m文件修改(对于PSO-PID算法) 运行程序 我印象中好像做过…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

从数据报表到决策大脑:AI重构电商决策链条
在传统电商运营中,决策链条往往止步于“数据报表层”:BI工具整合历史数据,生成滞后一周甚至更久的销售分析,运营团队凭经验预判需求。当爆款突然断货、促销库存积压时,企业才惊觉标准化BI的决策时差正成为增长瓶颈。 一…...

MCP和Function Calling
MCP MCP(Model Context Protocol,模型上下文协议) ,2024年11月底,由 Anthropic 推出的一种开放标准,旨在统一大模型与外部数据源和工具之间的通信协议。MCP 的主要目的在于解决当前 AI 模型因数据孤岛限制而…...
