MapSet之二叉搜索树
系列文章:
1. 先导片--Map&Set之二叉搜索树
2. Map&Set之相关概念
目录
前言
1.二叉搜索树
1.1 定义
1.2 操作-查找
1.3 操作-新增
1.4 操作-删除(难点)
1.5 总体实现代码
1.6 性能分析
前言
1.二叉搜索树
1.1 定义
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值若它的右子树不为空,则右子树上所有节点的值都大于根节点的值它的左右子树也分别为二叉搜索树

1.2 操作-查找
如果根节点不为空:
如果根节点key == 查看key 返回true
如果根节点key > 查看key 在其左子树查找
如果根节点key < 查看key 在其右子树查找
否则返回false
实现代码:
class BinarySearchTree {public static class Node {int key;Node left;Node right;public Node(int key) {this.key = key;}}private Node root = null;/*** 搜索* @param key* @return*/public Node search(int key) {Node cur = root;while (cur != null){if(cur.key == key){return cur;}else if (key < cur.key){cur = cur.left;}else{cur = cur.right;}}return null;}
}1.3 操作-新增
1.如果树为空树,即根 == null,直接插入
2.如果树不是空树,按照查找逻辑查找位置,插入新结点
实现代码:
class BinarySearchTree {public static class Node {int key;Node left;Node right;public Node(int key) {this.key = key;}}private Node root = null;/*** 插入** @param key* @return*/public boolean insert(int key) {Node cur = root;if (cur == null) {cur = new Node(key);return true;}Node parent = null;while (cur != null) {if (key == cur.key) {return false;} else if (key < cur.key) {parent = cur;cur = cur.left;} else {parent = cur;cur = cur.right;}}Node node = new Node(key);if (key < parent.key) {parent.right = node;} else {parent.left = node;}return true;}
}1.4 操作-删除(难点)
设待删除结点为cur,待删除结点的双亲结点为parent
1.cur.left == null;
1. cur 是 root ,则 root = cur.right2. cur 不是 root , cur 是 parent.left ,则 parent.left = cur.right3. cur 不是 root , cur 是 parent.right ,则 parent.right = cur.right

2.cur.right == null;
1. cur 是 root ,则 root = cur.left2. cur 不是 root , cur 是 parent.left ,则 parent.left = cur.left3. cur 不是 root , cur 是 parent.right ,则 parent.right = cur.left

3.cur.left != null && cur.right != null;
需要使用替换法进行删除,即在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题。

实现代码:
class BinarySearchTree {public static class Node {int key;Node left;Node right;public Node(int key) {this.key = key;}}private Node root = null;/*** 删除** @param key* @return*/public boolean delete(int key) {Node cur = root;Node parent = null;while (cur != null) {if (key == cur.key) {deleteValue(cur, parent);return true;} else if (key < cur.key) {parent = cur;cur = cur.left;} else {parent = cur;cur = cur.right;}}return false;}public void deleteValue(Node cur, Node parent) {//cur左右孩子都不在if (cur.left == null && cur.right == null) {if (parent.right == cur) {parent.right = null;} else {parent.left = null;}//cur左孩子不在}else if (cur.left == null) {if (cur == root) {root = root.right;} else if (cur == parent.right) {parent.right = cur.right;} else {parent.left = cur.right;}//cur右孩子不在}else if (cur.right == null) {if (cur == root) {root = root.left;} else if (cur == parent.right) {parent.right = cur.left;} else {parent.left = cur.left;}//左右均在}else{//为删除节点的右节点Node target = cur.right;Node targetParent = cur;//找右树最左节点while (target.left != null){targetParent = target;target = target.left;}cur.key = target.key;if(targetParent.left == target){targetParent.left = target.right;}else{targetParent.right = target.right;}}}
}1.5 总体实现代码
class BinarySearchTree {public static class Node {int key;Node left;Node right;public Node(int key) {this.key = key;}}private Node root = null;/*** 搜索** @param key* @return*/public Node search(int key) {Node cur = root;while (cur != null) {if (cur.key == key) {return cur;} else if (key < cur.key) {cur = cur.left;} else {cur = cur.right;}}return null;}/*** 插入** @param key* @return*/public boolean insert(int key) {Node cur = root;if (cur == null) {cur = new Node(key);return true;}Node parent = null;while (cur != null) {if (key == cur.key) {return false;} else if (key < cur.key) {parent = cur;cur = cur.left;} else {parent = cur;cur = cur.right;}}Node node = new Node(key);if (key < parent.key) {parent.right = node;} else {parent.left = node;}return true;}/*** 删除** @param key* @return*/public boolean delete(int key) {Node cur = root;Node parent = null;while (cur != null) {if (key == cur.key) {deleteValue(cur, parent);return true;} else if (key < cur.key) {parent = cur;cur = cur.left;} else {parent = cur;cur = cur.right;}}return false;}public void deleteValue(Node cur, Node parent) {//cur左右孩子都不在if (cur.left == null && cur.right == null) {if (parent.right == cur) {parent.right = null;} else {parent.left = null;}//cur左孩子不在}else if (cur.left == null) {if (cur == root) {root = root.right;} else if (cur == parent.right) {parent.right = cur.right;} else {parent.left = cur.right;}//cur右孩子不在}else if (cur.right == null) {if (cur == root) {root = root.left;} else if (cur == parent.right) {parent.right = cur.left;} else {parent.left = cur.left;}//左右均在}else{//为删除节点的右节点Node target = cur.right;Node targetParent = cur;//找右树最左节点while (target.left != null){targetParent = target;target = target.left;}cur.key = target.key;if(targetParent.left == target){targetParent.left = target.right;}else{targetParent.right = target.right;}}}
}1.6 性能分析
在二叉搜索树中,插入和删除操作都需要先进行查找。查找的效率直接影响了这些操作的性能。对于一个有n个节点的二叉搜索树,如果每个元素被查找的概率相等,那么平均查找长度将取决于节点在二叉搜索树中的深度。换句话说,节点越深,需要进行的比较次数就越多。
然而,对于相同的关键码集合,如果插入关键码的顺序不同,可能会得到不同结构的二叉搜索树。这是因为二叉搜索树的性质要求左子树的所有节点的值小于根节点的值,右子树的所有节点的值大于根节点的值。因此,不同的插入顺序可能会导致树的结构有所不同,从而影响查找效率。


相关文章:

MapSet之二叉搜索树
系列文章: 1. 先导片--Map&Set之二叉搜索树 2. Map&Set之相关概念 目录 前言 1.二叉搜索树 1.1 定义 1.2 操作-查找 1.3 操作-新增 1.4 操作-删除(难点) 1.5 总体实现代码 1.6 性能分析 前言 TreeMap 和 TreeSet 是 Java 中基于搜索树实现的 M…...

OpenCV图像分割教程
OpenCV 图像分割教程 OpenCV 是一个非常强大的计算机视觉库,支持各种图像处理任务。图像分割是 OpenCV 支持的一个重要功能,它用于将图像划分为不同的区域,识别感兴趣的部分。我们将通过介绍 OpenCV 中的图像分割方法,包括基础功…...

python科学计算:NumPy 线性代数与矩阵操作
1 NumPy 中的矩阵与数组 在 NumPy 中,矩阵实际上是一种特殊的二维数组,因此几乎所有数组的操作都可以应用到矩阵上。不过,矩阵运算与一般的数组运算存在一定的区别,尤其是在点积、乘法等操作中。 1.1 创建矩阵 矩阵可以通过 Nu…...

Unity面向对象补全计划 之 List<T>与class(非基础)
C# & Unity 面向对象补全计划 泛型-CSDN博客 关于List,其本质就是C#封装好的一个数组,是一个很好用的轮子,所以并不需要什么特别说明 问题描述 假设我们有一个表示学生的类 Student,每个学生有姓名和年龄两个属性。我们需要创…...

ant design vue+vue3+ts+xlsx实现表格导出问excel文件(带自定义表头)~
1、首先默认你已安装ant design vue、xlsx 库、及file-saver。 2、导入: import * as XLSX from xlsx; import { saveAs } from file-saver; 注:这里的xlsx导入不能这么写,否则会报错,原因是版本不一致,语法向上兼容…...
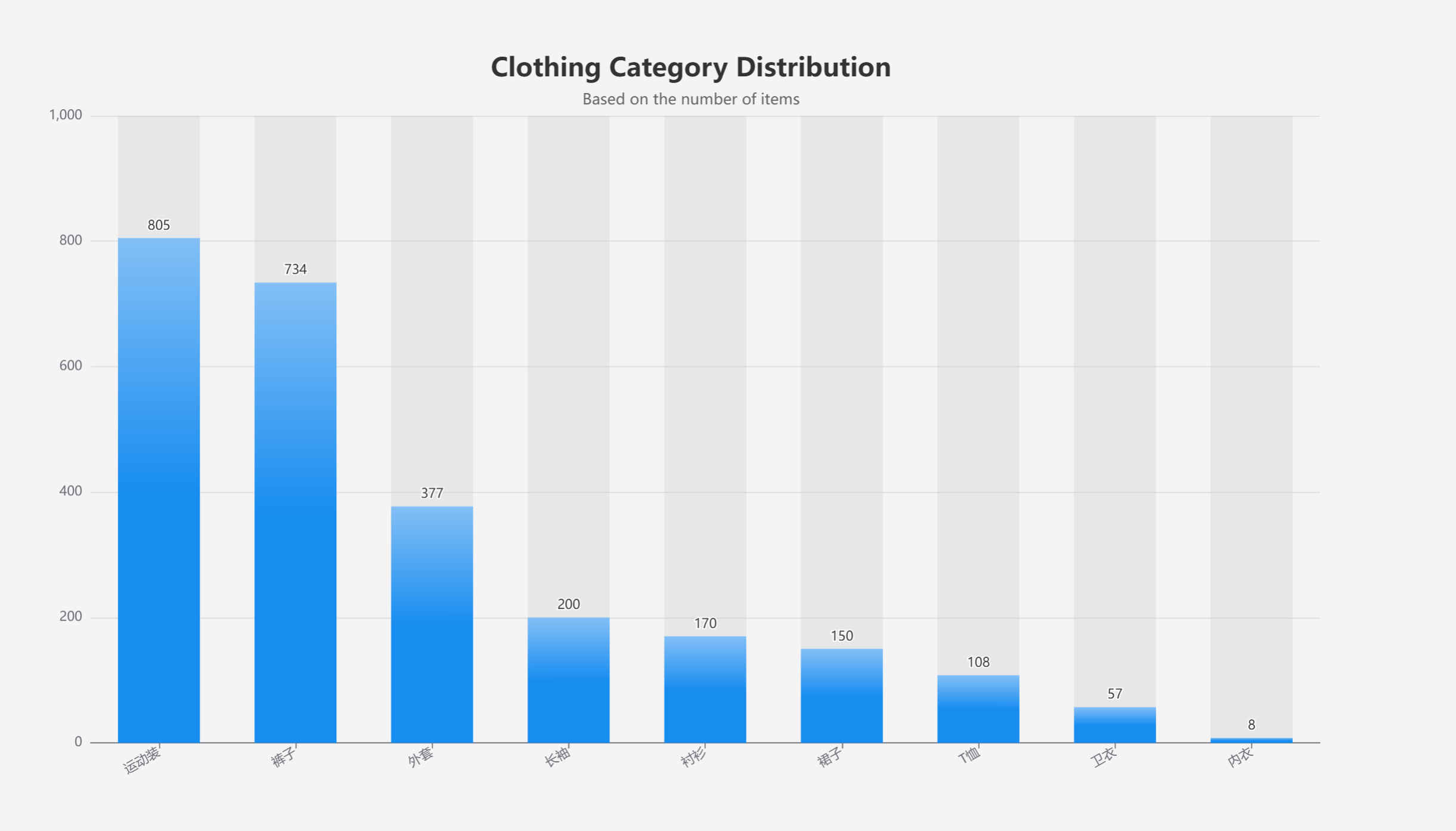
基于Python爬虫的淘宝服装数据分析项目
文章目录 一.项目介绍二.爬虫代码代码分析 三. 数据处理四. 数据可视化 一.项目介绍 该项目是基于Python爬虫的淘宝服装数据分析项目,以致于帮助商家了解当前服装市场的需求,制定更加精确的营销策略。首先,需要爬取淘宝中关于服装的大量数据…...

Tomcat控制台乱码问题已解决(2024/9/7
步骤很详细,直接上教程 问题复现: 情景一 情景二 原因简述 这是由于编码不一致引起的,Tomcat启动后默认编码UTF-8,而Windows的默认编码是GBK。因此你想让其不乱码,只需配置conf\logging.properties的编码格式即可 解决…...

vue通过html2canvas+jspdf生成PDF问题全解(水印,分页,截断,多页,黑屏,空白,附源码)
前端导出PDF的方法不多,常见的就是利用canvas画布渲染,再结合jspdf导出PDF文件,代码也不复杂,网上的代码基本都可以拿来即用。 如果不是特别追求完美的情况下,或者导出PDF内容单页的话,那么基本上也就满足业…...

服务器数据恢复—Raid磁盘阵列故障类型和常见故障原因
出于尽可能避免数据灾难的设计初衷,RAID解决了3个问题:容量问题、IO性能问题、存储安全(冗余)问题。从数据恢复的角度讨论RAID的存储安全问题。 常见的起到存储安全作用的RAID方案有RAID1、RAID5及其变形。基本设计思路是相似的:当部分数据异…...

C++字符串中的string类操作
愿我如星君如月,夜夜流光相皎洁。 ——《车逍遥篇》【宋】范成大 目录 正文: 主要特点: 基本操作: 代码演示: 总结: 今天我们接着上次的章节继续,这次我们来说一个为解决上个方法的缺陷而诞…...

axios设置responseType: ‘blob‘,获取接口返回的错误信息
在axios的请求中当后端接口返回的是文件流的情况下,我们需要在请求参数里面设置responseType: blob,如果接口报错,默认前端无法获取后端返回的错误信息。 解决方法:通过FileReader获取错误信息 async handleFetch() {const res aw…...

【C++】:模板初阶—函数模板|类模板
✨ Blog’s 主页: 白乐天_ξ( ✿>◡❛) 🌈 个人Motto:他强任他强,清风拂山岗! 💫 欢迎来到我的学习笔记! 本文参考博客:一同感受C模版的所带来的魅力 一、泛型编程思想 首先…...

Java 远程执行服务器上的命令
在Java中使用JSch库执行远程服务器上的命令是一种常见的做法,特别是在需要自动化运维任务或者进行远程文件操作时。以下是基于Codekru网站提供的示例,展示如何使用JSch库在远程服务器上执行单个或多个命令。 准备工作 首先,确保您的项目中已…...

3DMax基础- 创建基础模型
目录 零.软件简介 一. 标准基本型 长方体 圆锥体 球体 圆柱体 管状体 圆环 四棱锥 茶壶 平面编辑 加强型文本 二. 扩展基本体 三.复合对象 变形 散布 一致 连接 图形合并 布尔 并集 合并 交集 差集 四.门和窗 门 窗 植物,栏杆,墙 零.软件简介 3…...

JavaScript 知识点(从基础到进阶)
🌏个人博客主页:心.c 前言:JavaScript已经学完了,和大家分享一下我的笔记,希望大家可以有所收获,花不多说,开干!!! 🔥🔥ǵ…...

计算机网络知识点复习——TCP协议的三次握手与四次挥手(连接与释放)
TCP协议的三次握手与四次挥手(连接与释放) 一、前言二、简单的知识准备1. TCP协议的主要特点2. TCP报文段 三、TCP连接的建立(三次握手)四、TCP连接的释放(四次挥手)五、TCP连接与释放的总结六、结束语 一、…...

SpringDataJPA系列(7)Jackson注解在实体中应用
SpringDataJPA系列(7)Jackson注解在实体中应用 常用的Jackson注解 Springboot中默认集成的是Jackson,我们可以在jackson依赖包下看到Jackson有多个注解 一般常用的有下面这些: 一个实体的示例 测试方法如下: 按照上述图片中的序号做个简…...

【Spring Boot 3】【Web】统一封装 HTTP 响应体
【Spring Boot 3】【Web】统一封装 HTTP 响应体 背景介绍开发环境开发步骤及源码工程目录结构总结背景 软件开发是一门实践性科学,对大多数人来说,学习一种新技术不是一开始就去深究其原理,而是先从做出一个可工作的DEMO入手。但在我个人学习和工作经历中,每次学习新技术总…...

Linux如何做ssh反向代理
SSH反向代理是一种通过SSH协议实现的安全远程访问方式,它允许客户端通过SSH连接到一台具有公网IP的代理服务器,然后这台代理服务器再将请求转发给内部网络中的目标主机。以下是实现SSH反向代理的步骤: 一、准备工作 确保服务器配置ÿ…...

Verilog语法+:和-:有什么用?
Verilog语法:和-:主要用于位选择,可以让代码更简洁。 一、位选择基础 在Verilog中,位选择可以通过直接索引来实现,例如: reg [7:0] data; wire select_a; wire [2:0] select_b; assign select_a data[3]; assign select_b …...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...
