前缀和 — 利用前缀信息解决子数组问题
【前缀和的核心思想是预先处理数组来快速计算任意子数组的和,基本上用于数组和序列问题。】
前缀和算法具体步骤
-
构造前缀和数组:
- 给定一个数组
nums,其前缀和数组prex定义为prex[i]表示为数组nums从起始位置到第i个位置的元素累加和。 - 构建前缀和公式:
p r e x [ i ] = n u m s [ i ] ( i = = 0 ) p r e x [ i ] = p r e x [ i − 1 ] + n u m s [ i ] ( i > 0 ) prex[i] = nums[i] \quad (i == 0) \\ \\ prex[i] = prex[i-1] + nums[i] \quad (i > 0) prex[i]=nums[i](i==0)prex[i]=prex[i−1]+nums[i](i>0)
- 给定一个数组
-
快速计算子数组和:
- 一旦前缀和数组构建完成,就可以快速计算任意子数组
nums[i...j]的元素累加和。
s u m ( n u m s [ i . . . j ] ) = p r e x [ j ] − p r e x [ i − 1 ] ( i > 0 ) sum(nums[i...j]) = prex[j] - prex[i-1] \quad(i > 0) sum(nums[i...j])=prex[j]−prex[i−1](i>0)
- 当
i == 0时,子数组和也就是nums[0]。
- 一旦前缀和数组构建完成,就可以快速计算任意子数组
我们前面介绍过【滑动窗口算法】,滑动窗口算法也是基本用于数组和序列问题的,所以我们把【前缀和算法】与【滑动窗口算法】放在一起研究,也当作对滑动窗口算法的复习。
简要复习一下滑动窗口算法的步骤
【滑动窗口算法的核心思想就是维护一个固定长度的窗口,在数组或序列上滑动以满足某些条件。通常用于解决最大子数组和、最小子数组和等问题。】
-
初始化窗口:
设置窗口的起始和结束指针。
-
滑动窗口:
移动窗口的起始和结束指针,依据问题的要求调整窗口的大小,维护窗口的状态(例如窗口内元素的和,最大值,最小值等)。
[!TIP]
之前我们分析滑动窗口算法的时候就提到过,选择哪种数据结构来存储数据需要根据【窗口内的数据以及数据的处理形式】来考虑。
比如:
- 如果需要记录窗口中各字符以及各字符出现的次数,就用哈希表。
我们通过一个例子看深入了解一下前缀和算法:
LeetCode560 和为 K 的子数组
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。
子数组是数组中元素的连续非空序列。
示例 1:
输入:nums = [1,1,1], k = 2
输出:2
示例 2:
输入:nums = [1,2,3], k = 3
输出:2
提示:
1 <= nums.length <= 2 * 104-1000 <= nums[i] <= 1000-107 <= k <= 107
暴力解法
既然是找满足条件的子数组个数,那我们可以枚举所有的子数组,然后选出符合条件的子数组就行了。
int subarraySum(vector<int> &nums, int k) {int size = nums.size();int result = 0;for (int left = 0; left < size; left++) {for (int right = left; right < size; right++) {//这个时候窗口为 nums[left...right]int sum = 0;int cur = left;while (cur <= right) {sum += nums[cur];cur++;}if (sum == k)result++;}}return result;
}
暴力解法就是这么通俗易懂,找出每个子串,然后对每个子串单独进行分析就行了。但是暴力解法找子串的时间复杂度是 O ( N 2 ) O(N^2) O(N2),时间复杂度太高了,所以我们需要思考另一种解法。
前缀和分析思路:
联想刚刚学到的前缀和表示子数组,我们知道,子数组nums[i...j]之和不就是prex[j] - prex[i-1]嘛。也就是说,和为 K 的子数组满足等式
p r e x [ j ] − p r e x [ i − 1 ] = = K prex[j] - prex[i-1] == K prex[j]−prex[i−1]==K
但是按照这个等式思路,我们只是利用了前缀和来方便找出各个子串的和罢了,还是要变动i,j两个变量来查找和为 K 的子数组,时间复杂度还是 O ( N 2 ) O(N^2) O(N2),我们得到目标是什么?是要降低时间复杂度。很容易想到,既然变动两个变量的时间复杂度为 O ( N 2 ) O(N^2) O(N2),那我们就试试只变动一个变量,我们对上面公式进行变换:
p r e x [ i − 1 ] = = p r e x [ j ] − K prex[i-1] == prex[j] - K prex[i−1]==prex[j]−K
从这个公式,我们清楚,如果子串最右边字符的位置j确定,那么要想找到【和为 K 的子数组】的个数,只需找到前缀和数组中0,1,...j-1这些位置对应的值中有几个值等于 K − p r e x [ j ] K-prex[j] K−prex[j], 如果我们把这个查找的实践复杂度降为 O ( 1 ) O(1) O(1),那么总体的时间复杂度只消耗在j的变动上了嘛,也就降为了 O ( N ) O(N) O(N)。
怎么实现这个查找呢?和滑动窗口算法一样,面对不同的数据组织和变动情况,我们要选择合适的数据结构来帮助我们存储和查找数据。在这个题目中,因为要存储0,1,...,j-1的前缀和以及前缀和出现的次数,所以我们使用哈希表来存储数据,键代表j之前的各个前缀和,值代表此前缀和对应的数组出现的次数。
分析了这么多,最后我们只要移动j就行了,只需要对数组遍历一次。
我们给出前缀和解法:
int subarraySum(vector<int> &nums, int k) {//计数器,存储j之前数组和以及数组和出现的次数unordered_map<int,int> mp;mp[0]++; //数组为空,和自然为0int prex[nums.size()];int result = 0;for(int j = 0; j < nums.size(); j++){if(j == 0){prex[j] += nums[j];//查找j之前的数组和有几个满足条件if(mp.count(prex[j] - K)){result += mp[prex[j] - K];}mp[prex[j]]++;continue;}prex[j] = prex[j-1] + nums[j];if(mp.count(prex[j] - K)){result += mp[prex[j] - K];}mp[prex[j]]++;}return result;
}
这段代码便是我们利用【前缀和】和【哈希表】得到的解法,时间复杂度是降低了,空间复杂度能降低吗?
复盘这段代码,我们发现,在循环里,第'j'次循环只用到了prex[j]并不会用到前面的prex[0...j-1],所以我们不用再花费 O ( N ) O(N) O(N)的空间复杂度去维护前缀和数组prex[],直接用一个变量prex表示prex[j]即可。
改造后的代码:
int subarraySum(vector<int> &nums, int k) {//计数器,存储j之前数组和以及数组和出现的次数unordered_map<int,int> mp;mp[0]++; //数组为空,和自然为0int prex = 0;int result = 0;for(int num : nums){prex += num;if(mp.count(prex - K)){result += mp[prex - K];}mp[prex]++;}return result;
}
到这里,你基本上掌握了前缀和的思想了,但是要注意的是:
[!IMPORTANT]
前缀和只是我们用来表示子数组的一种方法而已,遇到具体问题,我们要找出问题的本质,子数组间有什么关系?最好能找出具体公式出来,比如这道【和为 K 的子数组】题目,我们就是找出了公式
p r e x [ j ] − p r e x [ i − 1 ] = = K prex[j] - prex[i-1] == K prex[j]−prex[i−1]==K
之后对这个公式进行分析,进行合适的变换。
1248 454
【我们再看两道题来巩固一下【前缀和】与其他数据结构结合的算法思想】
LeetCode523 连续的子数组
一个 好的子数组 是:
- 长度 至少为 2 ,且
- 子数组元素总和为
k的倍数。
注意:
- 子数组 是数组中 连续 的部分。
- 如果存在一个整数
n,令整数x符合x = n * k,则称x是k的一个倍数。0始终 视为k的一个倍数。
示例 1:
输入:nums = [23,2,4,6,7], k = 6
输出:true
解释:[2,4] 是一个大小为 2 的子数组,并且和为 6 。
示例 2:
输入:nums = [23,2,6,4,7], k = 6
输出:true
解释:[23, 2, 6, 4, 7] 是大小为 5 的子数组,并且和为 42 。
42 是 6 的倍数,因为 42 = 7 * 6 且 7 是一个整数。
示例 3:
输入:nums = [23,2,6,4,7], k = 13
输出:false
提示:
1 <= nums.length <= 1050 <= nums[i] <= 1^090 <= sum(nums[i]) <= 2^31 - 11 <= k <= 2^31 - 1
分析过程:
这道题算是【和为 K 的子数组】的变式,求【和为 K 的整数倍的子数组】,我们先考虑迁移【和为 K 的子数组的解法】。
得出公式:
p r e x [ j ] − p r e x [ i − 1 ] = = λ ∗ K p r e x [ i − 1 ] = = p r e x [ j ] − λ ∗ K prex[j] - prex[i-1] == λ*K \\ prex[i-1] ==prex[j] - λ*K prex[j]−prex[i−1]==λ∗Kprex[i−1]==prex[j]−λ∗K
解法框架如下:
bool checkSubarraySum(vector<int> &nums, int k) {//计数器,存储j之前数组和以及数组和出现的次数unordered_map<int,int> mp;mp[0]++; //数组为空,和自然为0int prex = 0;int result = 0;for(int num : nums){prex += num;if(mp.count(prex - lamda*K)){result += mp[prex - lamda*K];}mp[prex]++;}return result > 0;
}
我们怎么确定这个 l a m d a lamda lamda呢?要枚举 l a m d a lamda lamda的取值并代入吗? l a m d a lamda lamda取值为 0 , . . . , [ p r e x / X ] 0,...,[prex/X] 0,...,[prex/X]。或者遍历mp里的每个键,查看prex是否能整除X。
上面的分析只分析了子数组的数组和可能为 K 的倍数,子数组的长度至少为 2,这个要求我们并没有考虑。和子数组长度有关的话,哈希表存储前缀和以及前缀和出现的次数就不能用了,因为哈希表里的前缀和nums[0...i]并不能确定是i是什么,我们只是将前缀和的值一股脑放进哈希表里而已。
所以我们现在要改变数据存储形式,要么使用别的数据结构,要么将哈希表里的键值对对应的数据改为其他数据。所以现在,我们要体现出【前缀和】,以及【前缀和对应的位置nums[0...i](i)】和【出现的次数】。怎么体现呢?按照之前思路,我们是在遍历prex[j],在遍历的同时,将{前缀和:{位置,出现次数}}存入哈希表中。
解法如下:
bool checkSubarraySum(vector<int> &nums, int k) {//计数器,存储j之前数组和以及数组和出现的次数unordered_map<int,pair<int,int>> mp;mp[0] = {-1,1}; //数组为空,和自然为0int prex = 0;int result = 0;for(int j = 0;j < nums.size();j++){prex += nums[j];//遍历哈希表,查看是否存在这样一个前缀和,使得prex与这个前缀和之差是K的倍数,且满足长度大于等于2for(const auto& element : mp){if((prex - element.first)% k == 0){if(element.second.first < j - 1){result += element.second.second;}}}mp[prex] = {j,mp[prex]+1}; //?}return result > 0;
}
接下来看看二维以及多维的前缀和是如何使用的
二维前缀和
【二维前缀和】和【一维前缀和】一样,也是记录前面数组元素的累加和。对于一维而言,就是前 0 , 1 , . . . , i − 1 0,1,...,i-1 0,1,...,i−1这些位置对应的元素的累加和,二维也是一样,前 0 < = m < i , 0 < = n < j , ( m , n ) 0 <= m < i, 0 <= n < j,(m,n) 0<=m<i,0<=n<j,(m,n) 这些位置对应的元素累加和,其实也就是以 ( i , j ) (i,j) (i,j) 为右下角的正方形左上方的所有元素之和。同样,我们给出二维前缀和数组以及递推公式:
二维前缀和具体步骤
-
构建二维前缀和数组
- 给定一个二维数组
matrix,其前缀和数组定义为preSum[i][j]表示以(0,0)为左上角,(i,j)为右下角的矩形内所有元素之和。 - 构建二维前缀和公式:
p r e S u m [ 0 ] [ 0 ] = m a t r i x [ 0 ] [ 0 ] p r e S u m [ 0 ] [ j ] = p r e S u m [ 0 ] [ j − 1 ] + m a t r i x [ 0 ] [ j ] ( i = = 0 , j > 0 ) p r e S u m [ i ] [ 0 ] = p r e S u m [ i − 1 ] [ 0 ] + m a t r i x [ i ] [ 0 ] ( i > 0 , j = = 0 ) p r e S u m [ i ] [ j ] = p r e S u m [ i − 1 ] [ j ] + p r e S u m [ i ] [ j − 1 ] − p r e S u m [ i − 1 ] [ j − 1 ] + m a t r i x [ i ] [ j ] ( i > 0 , j > 0 ) preSum[0][0] = matrix[0][0] \\ preSum[0][j] = preSum[0][j-1] + matrix[0][j]\quad(i == 0, j > 0)\\ preSum[i][0] = preSum[i-1][0] + matrix[i][0]\quad(i>0,j==0)\\ preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] - preSum[i-1][j-1] + matrix[i][j]\quad(i>0,j>0) preSum[0][0]=matrix[0][0]preSum[0][j]=preSum[0][j−1]+matrix[0][j](i==0,j>0)preSum[i][0]=preSum[i−1][0]+matrix[i][0](i>0,j==0)preSum[i][j]=preSum[i−1][j]+preSum[i][j−1]−preSum[i−1][j−1]+matrix[i][j](i>0,j>0)
- 给定一个二维数组
-
优化后的二维前缀和数组
我们发现,上面的二维前缀和公式过于麻烦,需要分类讨论四种情况,这四种情况都是边界处的情况。所以我们现在弱化边界,在边界之外再套一层,在原来的二维数组左上方套一层,套上的每一个元素都是 0,这样就不会影响前缀和数组的数值。
- 优化后的数组定义:
preSum[i][j]表示以(0,0)为左上角,(i-1,j-1)为右下角的矩形内所有元素之和。preSum[0][0...n],preSum[0...n][0]这些元素都赋值 0,这也就是我们上面说的套上一层辅助数据,这些数据都是 0。 - 二维前缀和公式:
p r e S u m [ i ] [ j ] = p r e S u m [ i − 1 ] [ j ] + p r e S u m [ i ] [ j − 1 ] − p r e S u m [ i − 1 ] [ j − 1 ] + m a t r i x [ i − 1 ] [ j − 1 ] ( i > = 1 , j > = 1 ) preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] - preSum[i-1][j-1] + matrix[i-1][j-1]\quad(i>=1,j>=1) preSum[i][j]=preSum[i−1][j]+preSum[i][j−1]−preSum[i−1][j−1]+matrix[i−1][j−1](i>=1,j>=1)
优化后的数组,
preSum[i][j]对应matrix[i-1][j-1]为右下角的矩形元素累加和。 - 优化后的数组定义:
-
快速计算区域子矩阵和(多维数组叫着有点别扭,后面都会用矩阵代替多维数组)
得出前缀和矩阵后,我们可以利用前缀和矩阵快速计算出子矩阵中元素累加和。如果子矩阵的左上角为
(m,n),右下角为(i,j),那么我们可以直接利用公式:S u b M a t r i x S u m = p r e S u m [ i ] [ j ] − p r e S u m [ i ] [ n − 1 ] − p r e S u m [ m − 1 ] [ j ] + p r e S u m [ m − 1 ] [ n − 1 ] SubMatrixSum = preSum[i][j] - preSum[i][n-1] - preSum[m-1][j] + preSum[m-1][n-1] SubMatrixSum=preSum[i][j]−preSum[i][n−1]−preSum[m−1][j]+preSum[m−1][n−1]
这里是利用了优化后的前缀和数组来进行分析,
i,j的取值为 1... n 1...n 1...n。
我们来看一道题目,充分理解二维前缀和
LeetCode1314 矩阵区域和
给你一个 m x n 的矩阵 mat 和一个整数 k ,请你返回一个矩阵 answer ,其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和:
i - k <= r <= i + k,j - k <= c <= j + k且(r, c)在矩阵内。
示例 1:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出:[[12,21,16],[27,45,33],[24,39,28]]
示例 2:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2
输出:[[45,45,45],[45,45,45],[45,45,45]]
提示:
m == mat.lengthn == mat[i].length1 <= m, n, k <= 1001 <= mat[i][j] <= 100
问题分析:
我们很容易看出,answer[i][j]表示的就是以[i][j]为中心,边长为 2 ∗ k + 1 2*k+1 2∗k+1的正方形内的所有元素之和。对照刚刚讲的二维前缀矩阵,这个正方形可以由什么表示呢?
int start_i = std::max(i-k,0);
int start_j = std::max(j-k,0);
int end_i = std::min(m-1,i+k);
int end_j = std::min(n-1,j+k);
其实这个“正方形”中的元素就是以start_i,start_j为左上角,end_i,end_j为右下角的矩形中的所有元素。answer[i][j]存的就是这个矩形中所有元素的累加和嘛。这个累加和我们直接用递推公式就可以得出来:
S u b M a t r i x S u m = p r e S u m [ e n d i + 1 ] [ e n d j + 1 ] − p r e S u m [ e n d i + 1 ] [ s t a r t j − 1 + 1 ] − p r e S u m [ s t a r t i − 1 + 1 ] [ e n d j + 1 ] + p r e S u m [ s t a r t i − 1 + 1 ] [ s t a r t j − 1 + 1 ] SubMatrixSum = preSum[end_i+1][end_j+1] - preSum[end_i+1][start_j-1+1] \\ - preSum[start_i-1+1][end_j+1] + preSum[start_i-1+1][start_j-1+1] SubMatrixSum=preSum[endi+1][endj+1]−preSum[endi+1][startj−1+1]−preSum[starti−1+1][endj+1]+preSum[starti−1+1][startj−1+1]
这里的(i,j)是基于原矩阵matrix的。
现在我们给出最终代码:
vector <vector<int>> matrixBlockSum(vector <vector<int>> &mat, int k) {int m = mat.size();int n = mat[0].size();vector <vector<int>> answer(m, vector<int>(n));//创建前缀和矩阵int preSum[m + 1][n + 1];for (int j = 0; j <= n; j++) {preSum[0][j] = 0;}for (int i = 0; i <= m; i++) {preSum[i][0] = 0;}//为前缀和矩阵赋值for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {preSum[i + 1][j + 1] = preSum[i][j + 1] + preSum[i + 1][j]- preSum[i][j] + mat[i][j];}}//为answer矩阵赋值for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {int start_i = std::max(i-k,0);int start_j = std::max(j-k,0);int end_i = std::min(m-1,i+k);int end_j = std::min(n-1,j+k);answer[i][j] = preSum[end_i + 1][end_j + 1] - preSum[end_i + 1][start_j]- preSum[start_i][end_j + 1] + preSum[start_i][start_j];}}return answer;
}
注意!!!,前缀和只是一种求子数组和子矩阵的方法而已,当遇到需要求解子数组或者子矩阵的问题时,如果需要用到子数组或者子矩阵中的元素,可以使用前缀和来表示子数组或者子矩阵。
相关文章:

前缀和 — 利用前缀信息解决子数组问题
【前缀和的核心思想是预先处理数组来快速计算任意子数组的和,基本上用于数组和序列问题。】 前缀和算法具体步骤 构造前缀和数组: 给定一个数组nums,其前缀和数组prex定义为prex[i]表示为数组nums从起始位置到第i个位置的元素累加和。构建前…...
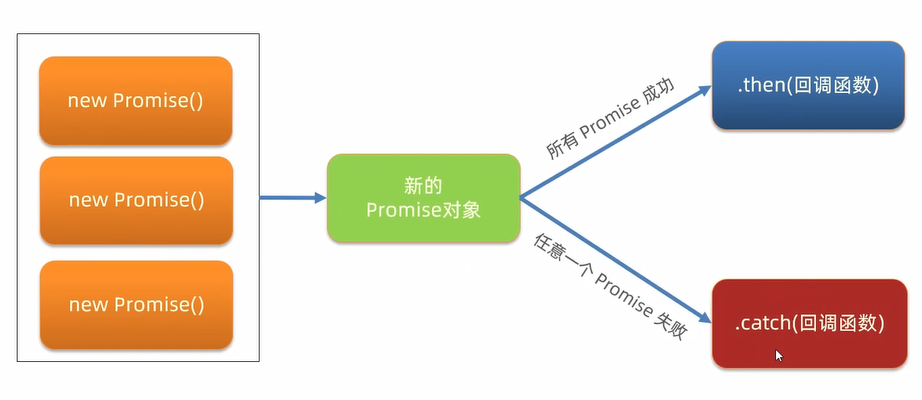
2024年最新版Ajax+Axios 学习【包含原理、Promise、报文、接口等...】
基础知识 AJAX概念 AJAX概念:是浏览器与服务器进行数据通信的技术。 认识URL 定义:统一资源定位符,简称网址,用于访问网络上的资源。 组成: http协议:超文本传输协议,规定浏览器和服务器之…...

【Qt线程】—— Qt线程详解
目录 (一)多线程的概述 (二)Qt线程的使用条件 (三)创建线程的方法 3.1 继承QTread,重写run()函数 3.1.1 为什么要重写 3.2 继承QObject 3.3 核心API介绍 3.4 关闭线程的使用方法 &…...

Golang | Leetcode Golang题解之第391题完美矩形
题目: 题解: func isRectangleCover(rectangles [][]int) bool {type point struct{ x, y int }area, minX, minY, maxX, maxY : 0, rectangles[0][0], rectangles[0][1], rectangles[0][2], rectangles[0][3]cnt : map[point]int{}for _, rect : range…...

〖open-mmlab: MMDetection〗解析文件:mmdet/models/detectors/two_stage.py
目录 MMDetection中的两阶段检测器:深入解析two_stage.py源码两阶段检测器概述two_stage.py的关键组件类定义和初始化构造函数Neck头配置RPN头配置RoI头配置_load_from_state_dict方法概述参数解释代码解析 特征提取方法签名文档字符串(Docstring&#x…...

【最新华为OD机试E卷-支持在线评测】机器人活动区域(100分)多语言题解-(Python/C/JavaScript/Java/Cpp)
🍭 大家好这里是春秋招笔试突围 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-E/D卷的三语言AC题解 💻 ACM金牌🏅️团队| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 🍿 最新华为OD机试D卷目录,全、新、准,题目覆盖率达 95% 以上,…...

C语言:刷题日志(1)
一.阶乘计算升级版 本题要求实现一个打印非负整数阶乘的函数。 其中n是用户传入的参数,其值不超过1000。如果n是非负整数,则该函数必须在一行中打印出n!的值,否则打印“Invalid input”。 首先,知道阶乘是所有小于及等于该数的…...
导入失败,Windows OpenSSl 1.1.1 下载)
ios私钥证书(p12)导入失败,Windows OpenSSl 1.1.1 下载
ios私钥证书(p12)导入失败 如果你用的OpenSSL版本是v3那么恭喜你V3必然报这个错,解决办法将OpenSSL 3降低成 v1。 Windows OpenSSl 1.1.1 下载 阿里云网盘下载地址:OpenSSL V1...

嵌入式面试经典30问:二
1. 嵌入式系统中,如何选择合适的微控制器或微处理器? 在嵌入式系统中选择合适的微控制器(MCU)或微处理器(MPU)时,需要考虑多个因素以确保所选组件能够满足项目的具体需求。以下是一些关键步骤和…...

目标检测-YOLOv1
YOLOv1介绍 YOLOv1(You Only Look Once version 1)是一种用于目标检测的深度学习算法,由Joseph Redmon等人于2016年提出。它基于单个卷积神经网络,将目标检测任务转化为一个回归问题,通过在图像上划分网格并预测每个网…...

python基础语法八-异常
书接上回: python基础语法一-基本数据类型 python基础语法二-多维数据类型 python基础语法三-类 python基础语法四-数据可视化 python基础语法五-函数 python基础语法六-正则匹配 python基础语法七-openpyxl操作excel 1. 异常简介 (1)异常:遇到…...

【堆的应用--C语言版】
前面一节我们都已将堆的结构(顺序存储)已经实现,对树的相关概念以及知识做了一定的了解。其中我们在实现删除操作和插入操作的时候,我们还同时实现了建大堆(小堆)的向上(下)调整算法…...

【微信小程序】搭建项目步骤 + 引入Tdesign UI
目录 创建1个空文件夹,选择下图基础模板 开启/支持sass 创建公共style文件并引入 引入Tdesign UI: 1. 初始化: 2. 安装后,开发工具进行构建: 3. 修改 app.json 4. 使用 5. 自定义主题色 创建1个空文件夹,选择下…...

android系统源码12 修改默认桌面壁纸--SRO方式
1、aosp12修改默认桌面壁纸 代码路径 :frameworks\base\core\res\res\drawable-nodpi 替换成自己的图片即可,不过需要覆盖所有目录下的图片。 由于是静态修改,则需要make一下,重新编译。 2、方法二Overlay方式 由于上述方法有…...

Echarts可视化
echarts是一个基于javascripts的开源可视化图表库 画图步骤: 1.引入echarts.js文件 <script src" https://cdn.jsdelivr.net/npm/echarts5.5.1/dist/echarts.min.js"></script> 也可将文件下载到本地通过src引入。 2. 准备一个呈现图表的…...

验证linux gpu是否可用
通过torch验证 import torchprint(torch.__version__) # 查看torch当前版本号 print(torch.version.cuda) # 编译当前版本的torch使用的cuda版本号 print(torch.cuda.is_available()) # 查看当前cuda是否可用于当前版本的Torch,如果输出True,则表示可…...

JavaScript( 简介)
目录 含义 实例 js代码位置 1 外部引入js文件 2 在 HTML 中,JavaScript 代码必须位于 标签之间。 小结 含义 js是一门脚本语言,能够改变HTML内容 实例 getElementById() 是多个 JavaScript HTML 方法之一。 本例使用该方法来“查找” id"d…...

Linux中的编译器gcc/g++
目录 一、gcc与g的区别 1.gcc编译器使用 2.g编译器使用 二、gcc/g编译器编译源文件过程 1.预处理 2.编译 3.汇编 4.链接 三、静态库和动态库 1.库中的头文件作用 2.静态库 3.动态库 四、gcc编译器的一些选项命令 一、gcc与g的区别 gcc用于编译C语言代码ÿ…...

RK3568安装部署Docker容器
设置华为镜像源 sudo sed -i s/huaweicloud.com/ustc.edu.cn/g /etc/apt/sources.list更新索引 rootok3568:/home/forlinx# sudo apt-get update Hit:1 http://ports.ubuntu.com/ubuntu-ports focal InRelease Hit:2 http://ports.ubuntu.com/ubuntu-ports focal-updates InR…...

Ubuntu 常用指令和作用解析
Ubuntu 常用指令和作用解析 Ubuntu 是一种常见的 Linux 发行版,它利用了 Unix 的力量和开源软件的精神。掌握常用指令可以提高我们在使用 Ubuntu 时的效率。本文将介绍一些常见的指令及其用途。 目录 更新与安装软件文件与目录操作系统信息与资源监控用户与权限管…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...
