当前位置：首页 > news >正文

一些数学经验总结——关于将原一元二次函数增加一些限制条件后最优结果的对比（主要针对公平关切相关的建模）

news 2026/2/9 20:39:34

1.没有分段的情况

原函数为一元二次凹函数（开口向下），如下：

$f_0(x)=(ax-b)(d-cx), where\ a>0,b>0,c>0, d>0, and\ \frac{b}{a} < \frac{d}{c}.$

因为要使得其存在正解，必须满足 $\frac{b}{a} < x < \frac{d}{c}$ ，那么 $\frac{b}{a} < \frac{d}{c}$ 。

上述函数的最优结果为： $x^*=\frac{a d+b c}{2 a c}$ ， $f(x^*)=\frac{a^2 d^2-2 a b c d+b^2 c^2}{4 a c}$ 。

对应的mathematica代码如下：

Clear["Global`*"]
f0[x_, a_, b_, c_, d_] := (a*x - b)*(d - c*x);(*(b c+a d)/(2 a c)*)
Maximize[{f1[x, a, b, c, d], a > 0 && b > 0 && c > 0 && d > 0}, x]

对应的mathematica结果如下：

2. 两个分段的情况

其中，

（1）第一个分段的函数为原函数；

（2）第二分段的函数为原函数的变体，即：
（i）第一因式与原函数的第一因式一样，即都为 $ax-b$ ;

（ii）第二因式在原函数的第二因式基础上减去一部分（即 $ex-f$ ），即为 $(d-cx)-(ex-f)$ ；

（3）其中分段点为减去部分为零时候的x值（即 $ex-f=0\Rightarrow x=\frac{f}{e}$ ）

$\begin{array}{l} F(x) = \left\{ {\begin{array}{*{20}{c}} {{f_0}(x)}&{x \le \frac{{{f_1}}}{{{e_1}}}}\\ {{f_{1}}(x)}&{x > \frac{{{f_1}}}{{{e_1}}}} \end{array}} \right. = \left\{ {\begin{array}{*{20}{c}} {(ax - b)(d - cx)}&{x \le \frac{{{f_1}}}{{{e_1}}}}\\ {(ax - b)[(d - cx) - ({e_1}x - {f_1})]}&{x > \frac{{{f_1}}}{{{e_1}}}} \end{array}} \right.\\ = \left\{ {\begin{array}{*{20}{c}} {(ax - b)(d - cx)}&{x \le \frac{{{f_1}}}{{{e_1}}}}\\ {(ax - b)[(d + {f_1}) - (c + {e_1})x]}&{x > \frac{{{f_1}}}{{{e_1}}}.} \end{array}} \right. \end{array}$

$where\ a>0,b>0,c>0, d>0, \frac{b}{a} < \frac{d}{c}, e_1>0, f_1>0, and\ \frac{b}{a} < \frac{{d + {f_1}}}{{c + {e_1}}}.$

针对第一分段 $f_0(x)$ ，在无限制条件情况下，最优结果为： $x^*=\frac{a d+b c}{2 a c}$ ， $f_0(x^*)=\frac{a^2 d^2-2 a b c d+b^2 c^2}{4 a c}$ 。

针对第二分段 $f_1(x)$ ，在无限制条件情况下，最优结果为： ${x^*} = \frac{{(ad + bc) + (a{f_1} + b{e_1})}}{{2(ac + a{e_1})}}$ ， $f_1(x^*)={\frac{{{{(b(c + e_1) - a(d + f_1))}^2}}}{{4a(c + e_1)}}}$ 。

外生参数的大小关系（可以利用mathematica验证）：

（1）成立的一些：

（i） $\frac{b}{a}<\frac{a d+b c}{2 a c}<\frac{d}{c}$ ；

（ii） $\frac{b}{a} < \frac{{\left( {bc + ad} \right) + \left( {b{e_1} + af_1} \right)}}{{2\left( {ac + a{e_1}} \right)}} < \frac{{d + {f_1}}}{{c + {e_1}}}$ 。

（2）不成立的一些：

（i） $\frac{{ad + bc}}{{2ac}} < \frac{{{f_1}}}{{{e_1}}} < \frac{{(ad + bc) + (a{f_1} + b{e_1})}}{{2(ac + a{e_1})}}$ ；

（ii） $\frac{{{f_1}}}{{{e_1}}} < \frac{{ad + bc}}{{2ac}} < \frac{{(ad + bc) + (a{f_1} + b{e_1})}}{{2(ac + a{e_1})}}$ 。

mathematica的代码如下：

Clear["Global`*"]
f0[x_, a_, b_, c_, d_] := (a*x - b)*(d - c*x);(*(b c+a d)/(2 a c)*)
f1[x_, a_, b_, c_, d_, e1_, f1_] := (a*x - b)*((d - c*x) - (e1*x - f1));(*((b c+a d)+(b e+a f))/(2 (a c+a e) )*)
(*f1[x_,a_,b_,c_,d_,e1_,f1_]:=(a*x-b)*((d+f1)-(c+e1)*x);*)Fx[x_, a_, b_, c_, d_, e1_, f1_] := Piecewise[{{f0[x, a, b, c, d], x <= f1/e1}, {f1[x, a, b, c, d, e1, f1], x > f1/e1}}];Reduce[a > 0 && b > 0 && c > 0 && d > 0 && e1 > 0 && f1 > 0 && b/a < d/c && b/a < (d + f1)/(c + e1)]Reduce[a > 0 && b > 0 && c > 0 && d > 0 && e1 > 0 && f1 > 0 && b/a < d/c && b/a < (d + f1)/(c + e1) && b/a < (b c + a d)/(2 a c) < d/c]
Reduce[a > 0 && b > 0 && c > 0 && d > 0 && e1 > 0 && f1 > 0 && b/a < d/c && b/a < (d + f1)/(c + e1) && b/a < ((b c + a d) + (b e1 + a f1))/(2 (a c + a e1) ) < (d + f1)/(c + e1)]
Reduce[a > 0 && b > 0 && c > 0 && d > 0 && e1 > 0 && f1 > 0 && b/a < d/c && b/a < (d + f1)/(c + e1) && (b c + a d)/(2 a c) < f1/e1 < ((b c + a d) + (b e1 + a f1))/(2 (a c + a e1) )]
Reduce[a > 0 && b > 0 && c > 0 && d > 0 && e1 > 0 && f1 > 0 && b/a < d/c && b/a < (d + f1)/(c + e1) && f1/e1 < (b c + a d)/(2 a c) < ((b c + a d) + (b e1 + a f1))/(2 (a c + a e1) )](*Reduce[a>0&&b>0&&c>0&&d>0&&e1>0&&f1>0&&b/a<d/c&&b/a<(d+f1)/(c+e1)&&(\
b c+a d)/(2 a c)>f1/e1&&f1/e1<((b c+a d)+(b e1+a f1))/(2 (a c+a e1) \
)&&f1[((b c+a d)+(b e1+a f1))/(2 (a c+a e1) ),a,b,c,d,e1,f1]>f0[(b \
c+a d)/(2 a c),a,b,c,d]]*)

比较重要的结论：

（1）当 $\frac{{ad + bc}}{{2ac}} \le \frac{{{f_1}}}{{{e_1}}}$ ，那么最优的结果为 ${x^*} = \frac{{ad + bc}}{{2ac}}$ 。

（2）当 $\frac{{ad + bc}}{{2ac}} > \frac{{{f_1}}}{{{e_1}}}$ ，

（2.1）当 $\frac{{(ad + bc) + (a{f_1} + b{e_1})}}{{2(ac + a{e_1})}} \le \frac{{{f_1}}}{{{e_1}}}$ ，那么最优的结果为 ${x^*} = \frac{{{f_1}}}{{{e_1}}}$ ，注意 ${f_0}(\frac{{ad + bc}}{{2ac}}) > {f_0}(\frac{{{f_1}}}{{{e_1}}})$ ；

（2.2）当 $\frac{{(ad + bc) + (a{f_1} + b{e_1})}}{{2(ac + a{e_1})}} > \frac{{{f_1}}}{{{e_1}}}$ ，那么最优的结果为 ${x^*} = \frac{{(ad + bc) + (a{f_1} + b{e_1})}}{{2(ac + a{e_1})}}$ ，注意 ${f_0}(\frac{{ad + bc}}{{2ac}}) > {f_1}(\frac{{(ad + bc) + (a{f_1} + b{e_1})}}{{2(ac + a{e_1})}})$ （可以利用mathematica验证）。

那么，总而言之，我们可以得出 $F(x)\leq f_0(x)$ ，当且仅当 ${x^*} = \frac{{ad + bc}}{{2ac}}$ 时，等号取到，即 $F(x)= f_0(x)$ 。

mathematica的代码如下：

Clear["Global`*"]
f0[x_, a_, b_, c_, d_] := (a*x - b)*(d - c*x);(*(b c+a d)/(2 a c)*)
f1[x_, a_, b_, c_, d_, e1_, f1_] := (a*x - b)*((d - c*x) - (e1*x - f1));(*((b c+a d)+(b e+a f))/(2 (a c+a e) )*)
(*f1[x_,a_,b_,c_,d_,e1_,f1_]:=(a*x-b)*((d+f1)-(c+e1)*x);*)Fx[x_, a_, b_, c_, d_, e1_, f1_] := Piecewise[{{f0[x, a, b, c, d], x <= f1/e1}, {f1[x, a, b, c, d, e1, f1], x > f1/e1}}];(*Reduce[a>0&&b>0&&c>0&&d>0&&e1>0&&f1>0&&b/a<d/c&&b/a<(d+f1)/(c+e1)]Reduce[a>0&&b>0&&c>0&&d>0&&e1>0&&f1>0&&b/a<d/c&&b/a<(d+f1)/(c+e1)&&b/\
a<(b c+a d)/(2 a c)<d/c]
Reduce[a>0&&b>0&&c>0&&d>0&&e1>0&&f1>0&&b/a<d/c&&b/a<(d+f1)/(c+e1)&&b/\
a<((b c+a d)+(b e1+a f1))/(2 (a c+a e1) )<(d+f1)/(c+e1)]
Reduce[a>0&&b>0&&c>0&&d>0&&e1>0&&f1>0&&b/a<d/c&&b/a<(d+f1)/(c+e1)&&(b \
c+a d)/(2 a c)<f1/e1<((b c+a d)+(b e1+a f1))/(2 (a c+a e1) )]
Reduce[a>0&&b>0&&c>0&&d>0&&e1>0&&f1>0&&b/a<d/c&&b/a<(d+f1)/(c+e1)&&f1/\
e1<(b c+a d)/(2 a c)<((b c+a d)+(b e1+a f1))/(2 (a c+a e1) )]*)Reduce[a > 0 && b > 0 && c > 0 && d > 0 && e1 > 0 && f1 > 0 && b/a < d/c && b/a < (d + f1)/(c + e1) && (b c + a d)/(2 a c) > f1/e1 && f1/e1 < ((b c + a d) + (b e1 + a f1))/(2 (a c + a e1) ) && f1[((b c + a d) + (b e1 + a f1))/(2 (a c + a e1) ), a, b, c, d, e1, f1] > f0[(b c + a d)/(2 a c), a, b, c, d]]

3. 三个分段的情况

其中，

（1）第一个分段的函数为原函数；

（2）第二分段的函数为原函数的变体，即：
（i）第一因式与原函数的第一因式一样，即都为 $ax-b$ ;

（ii）第二因式在原函数的第二因式基础上减去一部分（即 $ex-f$ ），即为 $(d-cx)-(e_1x-f_1)$ ；

（3）其中第二分段点为减去部分为零时候的x值（即 $e_1x-f_1=0\Rightarrow x=\frac{f_1}{e_1}$ ）

（4）第三分段的函数为原函数的变体，即：
（i）第一因式与原函数的第一因式一样，即都为 $ax-b$ ;

（ii）第二因式在原函数的第二因式基础上减去一部分（即 $e_2x - f_2$ ），即为 $(d-cx)-(e_2x-f_2)$ ；

（5）其中第三分段点为减去部分为零时候的x值（即 $e_2x-f_2=0\Rightarrow x=\frac{f_2}{e_2}$ ）

$\begin{array}{l} G(x) = \left\{ {\begin{array}{*{20}{c}} {{f_0}(x)}&{x \le \frac{{{f_1}}}{{{e_1}}}}\\ {{f_1}(x)}&{\frac{{{f_1}}}{{{e_1}}} < x \le \frac{{{f_2}}}{{{e_2}}}}\\ {{f_2}(x)}&{x > \frac{{{f_2}}}{{{e_2}}}} \end{array}} \right. = \left\{ {\begin{array}{*{20}{c}} {(ax - b)(d - cx)}&{x \le \frac{{{f_1}}}{{{e_1}}}}\\ {(ax - b)[(d - cx) - ({e_1}x - {f_1})]}&{\frac{{{f_1}}}{{{e_1}}} < x \le \frac{{{f_2}}}{{{e_2}}}}\\ {(ax - b)[(d - cx) - ({e_2}x - {f_2})]}&{x > \frac{{{f_2}}}{{{e_2}}}} \end{array}} \right.\\ = \left\{ {\begin{array}{*{20}{c}} {(ax - b)(d - cx)}&{x \le \frac{{{f_1}}}{{{e_1}}}}\\ {(ax - b)[(d + {f_1}) - (c + {e_1})x]}&{\frac{{{f_1}}}{{{e_1}}} < x \le \frac{{{f_2}}}{{{e_2}}}}\\ {(ax - b)[(d + {f_2}) - (c + {e_2})x]}&{x > \frac{{{f_2}}}{{{e_2}}}.} \end{array}} \right. \end{array}$

$where\ a>0,b>0,c>0, d>0, \frac{b}{a} < \frac{d}{c}, e_1>0, f_1>0, \frac{b}{a} < \frac{{d + {f_1}}}{{c + {e_1}}}, e_2>0, f_2>0, \frac{b}{a} < \frac{{d + {f_2}}}{{c + {e_2}}}, and\ \frac{{{f_1}}}{{{e_1}}} < \frac{{{f_2}}}{{{e_2}}}.$

针对第一分段 $f_0(x)$ ，在无限制条件情况下，最优结果为： $x^*=\frac{a d+b c}{2 a c}$ ， $f_0(x^*)=\frac{a^2 d^2-2 a b c d+b^2 c^2}{4 a c}$ ；

针对第二分段 $f_1(x)$ ，在无限制条件情况下，最优结果为： ${x^*} = \frac{{(ad + bc) + (a{f_1} + b{e_1})}}{{2(ac + a{e_1})}}$ ， $f_1(x^*)={\frac{{{{(b(c + e_1) - a(d + f_1))}^2}}}{{4a(c + e_1)}}}$ ；

针对第三分段 $f_2(x)$ ，在无限制条件情况下，最优结果为： ${x^*} = \frac{{(ad + bc) + (a{f_2} + b{e_2})}}{{2(ac + a{e_2})}}$ ， $f_2(x^*)={\frac{{{{(b(c + e_2) - a(d + f_2))}^2}}}{{4a(c + e_2)}}}$ 。

外生参数的大小关系（可以利用mathematica验证）：

（1）成立的一些：

（i） $\frac{b}{a}<\frac{a d+b c}{2 a c}<\frac{d}{c}$ ；

（ii） $\frac{b}{a} < \frac{{\left( {bc + ad} \right) + \left( {b{e_1} + af_1} \right)}}{{2\left( {ac + a{e_1}} \right)}} < \frac{{d + {f_1}}}{{c + {e_1}}}$ ；

（iii） $\frac{b}{a} < \frac{{\left( {bc + ad} \right) + \left( {b{e_2} + af_2} \right)}}{{2\left( {ac + a{e_2}} \right)}} < \frac{{d + {f_2}}}{{c + {e_2}}}$ 。

（2）不成立的一些：

（i） $\frac{{ad + bc}}{{2ac}} < \frac{{{f_1}}}{{{e_1}}} < \frac{{(ad + bc) + (a{f_1} + b{e_1})}}{{2(ac + a{e_1})}}$ ；

（ii） $\frac{{{f_1}}}{{{e_1}}} < \frac{{ad + bc}}{{2ac}} < \frac{{(ad + bc) + (a{f_1} + b{e_1})}}{{2(ac + a{e_1})}}$ ；

（i） $\frac{{ad + bc}}{{2ac}} < \frac{{{f_2}}}{{{e_2}}} < \frac{{(ad + bc) + (a{f_2} + b{e_2})}}{{2(ac + a{e_2})}}$ ；

（ii） $\frac{{{f_2}}}{{{e_2}}} < \frac{{ad + bc}}{{2ac}} < \frac{{(ad + bc) + (a{f_2} + b{e_2})}}{{2(ac + a{e_2})}}$ 。

比较重要的结论：

（1）当 $\frac{{ad + bc}}{{2ac}} \le \frac{{{f_1}}}{{{e_1}}}$ ，那么最优的结果为 ${x^*} = \frac{{ad + bc}}{{2ac}}$ 。

（2）当 $\frac{{ad + bc}}{{2ac}} > \frac{{{f_1}}}{{{e_1}}}$ ，

（2.1）当 $\frac{{(ad + bc) + (a{f_1} + b{e_1})}}{{2(ac + a{e_1})}} \le \frac{{{f_1}}}{{{e_1}}}$ ，那么第一分段与第二分段对比下最优的结果为 ${x^*} = \frac{{{f_1}}}{{{e_1}}}$ ，注意 ${f_0}(\frac{{ad + bc}}{{2ac}}) > {f_0}(\frac{{{f_1}}}{{{e_1}}})$ ；

（2.2）当 $\frac{{(ad + bc) + (a{f_1} + b{e_1})}}{{2(ac + a{e_1})}} > \frac{{{f_1}}}{{{e_1}}}$ ，那么第一分段与第二分段对比下最优的结果为 ${x^*} = \frac{{(ad + bc) + (a{f_1} + b{e_1})}}{{2(ac + a{e_1})}}$ ，注意 ${f_0}(\frac{{ad + bc}}{{2ac}}) > {f_1}(\frac{{(ad + bc) + (a{f_1} + b{e_1})}}{{2(ac + a{e_1})}})$ （可以利用mathematica验证）；

（3）当 $\frac{{ad + bc}}{{2ac}} > \frac{{{f_2}}}{{{e_2}}}$ ，

（3.1）当 $\frac{{(ad + bc) + (a{f_2} + b{e_2})}}{{2(ac + a{e_2})}} \le \frac{{{f_2}}}{{{e_2}}}$ ，那么第一分段与第三分段对比下最优的结果为 ${x^*} = \frac{{{f_2}}}{{{e_2}}}$ ，注意 ${f_0}(\frac{{ad + bc}}{{2ac}}) > {f_0}(\frac{{{f_1}}}{{{e_1}}})$ ；

（3.2）当 $\frac{{(ad + bc) + (a{f_2} + b{e_2})}}{{2(ac + a{e_2})}} > \frac{{{f_2}}}{{{e_2}}}$ ，那么第一分段与第三分段对比下最优的结果为 ${x^*} = \frac{{(ad + bc) + (a{f_2} + b{e_2})}}{{2(ac + a{e_2})}}$ ，注意 ${f_0}(\frac{{ad + bc}}{{2ac}}) > {f_2}(\frac{{(ad + bc) + (a{f_2} + b{e_2})}}{{2(ac + a{e_2})}})$ （可以利用mathematica验证）。

那么，总而言之，我们可以得出 $G(x)\leq f_0(x)$ ，当且仅当 ${x^*} = \frac{{ad + bc}}{{2ac}}$ 时，等号取到，即 $G(x)= f_0(x)$ 。

该结论可以扩展到N个分段的情况下，也就是N个分段的函数的最优结果不会优于原函数 $f_0(x)$ 的最优结果。

一些数学经验总结——关于将原一元二次函数增加一些限制条件后最优结果的对比（主要针对公平关切相关的建模）

1.没有分段的情况

2. 两个分段的情况

3. 三个分段的情况

相关文章：

一些数学经验总结——关于将原一元二次函数增加一些限制条件后最优结果的对比（主要针对公平关切相关的建模）

C++ | Leetcode C++题解之第394题字符串解码

getLocation:fail, the permission value is offline verifying

【数据分享】《中国城市统计年鉴》（1985-2023）全PDF版本第一次补档

什么是LED智能会议一体机?COB超微小间距LED会议一体机大势所趋

两种在wordpress网站首页调用woocommerce产品的方法

新一代交互模式：LUICUIVUI

chapter06 面向对象基础知识点Note

【Nginx系列】Nginx中rewrite模块

codesys进行控制虚拟轴运动时出现的一些奇怪bug的解释

前端框架有哪些

illusionX——一个从理解情感到改变学习、创新教育体验集成情感计算的混合现实系统

《黑暗之魂2:原罪学者》是什么类型的游戏《黑暗之魂》可以在苹果Mac电脑上玩吗？

使用C++20协程实现异步I/O操作：实战指南

MySQL之UDF提权复现

html记账本改写：保存数据 localStorage。

frida检测绕过-libmsaoaidsec.so

Splasthop 安全远程访问帮助企业对抗 Cobalt Strike 载荷网络攻击

Rust：Restful API 服务程序开发详述

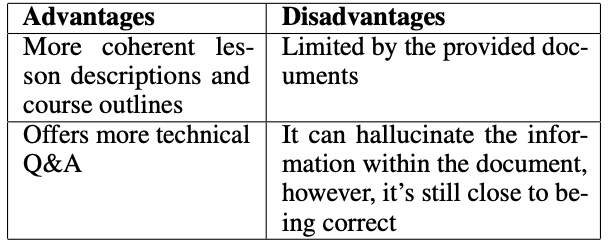
《Cloud Native Data Center Networking》（云原生数据中心网络设计）读书笔记 -- 09部署OSPF

AI-调查研究-01-正念冥想有用吗？对健康的影响及科学指南

渲染学进阶内容——模型

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力

Springcloud：Eureka 高可用集群搭建实战（服务注册与发现的底层原理与避坑指南）

ios苹果系统，js 滑动屏幕、锚定无效

重启Eureka集群中的节点，对已经注册的服务有什么影响

AGain DB和倍数增益的关系

Java毕业设计：WML信息查询与后端信息发布系统开发

【Linux】自动化构建-Make/Makefile

深度剖析 DeepSeek 开源模型部署与应用：策略、权衡与未来走向