6.3图的遍历
图的遍历是指从某点出发,按照某种搜索方式沿着边访问图中所有节点
图的遍历算法主要有两种:广度优先,深度优先
都需要辅助数组visited[]来记录节点是否被访问过
6.3.1广度优先搜索
like层次遍历,需要辅助队列
代码实现
#include<stdio.h>
#define maxnum 15
bool visited[maxnum];//定义辅助数组
void BFSTraverse(Graph G) {for (int i = 0; i < G.vexnum; i++){visited[i] = false;}//初始化数组initQueue(Q);//初始化队列for (int i = 0; i < G.vexnum; i++)//从0号顶点开始遍历{if (!visited[i]) {BFS(G,i);//广度优先遍历}}
}
void BFS(Graph G,int i){visit(i);//访问visited[i] = true;//改为tEnQueue(Q,i);//入队while (!isEmpty(Q)) {//判断队列是否为空DeQueue(Q,i);//输出队列第一个元素for ( p = FirstNeghbor(G,i); p >0; p=NextNeighbor(G,i,w)){if (!visited[p]) {visit(p);visited[p] = true;EnQueue(Q, p);}}}}广度优先遍历过程

从顶点1出发:12563748
从顶点3出发:34678215
性能分析
邻接表和邻接矩阵空间复杂度![]()
邻接表时间复杂度![]()
邻接矩阵的时间复杂度
广度优先生成树
在广度遍历中可以得到一颗遍历树,为广度优先生成树
邻接矩阵唯一,生成树唯一
邻接表不唯一,生成树不唯一

6.3.2深度优先搜索
belike树的先序遍历
代码实现
#include<stdio.h>
#define maxnum 15
bool visited[maxnum];//定义辅助数组
void DFSTraverse(Graph G) {for (int i = 0; i < G.vexnum; i++){visited[i] = false;}//初始化数组for (int i = 0; i < G.vexnum; i++)//从0号顶点开始遍历{if (!visited[i]) {DFS(G, i);//深度优先遍历}}
}
void DFS(Graph G, int i) {visit(i);//访问visited[i] = true;//改为tfor (p = FirstNeghbor(G, i); p > 0; p = NextNeighbor(G, i, w)){if (!visited[p]) {DFS(G, p);}
}深度优先遍历过程

从2出发:21563478
从3出发:34762158
性能分析

深度优先生成树和生成森林
非连通图可通过深度优先产生n棵生产树
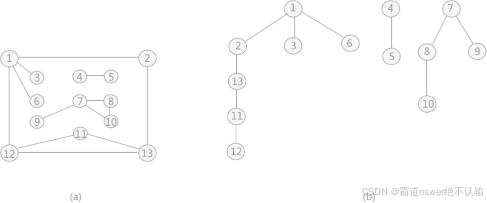
6.3.3图的遍历与图的连通性
to无向图:调用DFS/BFS的次数=连通分量数
to有向图:强连通分量只调用一次DFS/BFS;
若从起始节点到其他节点都有路径,则只需调用一次
相关文章:

6.3图的遍历
图的遍历是指从某点出发,按照某种搜索方式沿着边访问图中所有节点 图的遍历算法主要有两种:广度优先,深度优先 都需要辅助数组visited[]来记录节点是否被访问过 6.3.1广度优先搜索 like层次遍历,需要辅助队列 代码实现 #include<stdio.h> #define maxnum 15 bool vi…...

2024数学建模国赛选题建议+团队助攻资料(已更新完毕)
目录 一、题目特点和选题建议 二、模型选择 1、评价模型 2、预测模型 3、分类模型 4、优化模型 5、统计分析模型 三、white学长团队助攻资料 1、助攻代码 2、成品论文PDF版 3、成品论文word版 9月5日晚18:00就要公布题目了,根据历年竞赛题目…...

大学课程-人机交互期末复习
绪论 什么是人机交互技术?⭐⭐ 是指关于设计、评价和实现供人们使用的交互式计算机系统,并围绕相关的主要现象进行研究的学。狭 义的讲,人机交互技术主要是研究人与计算机之间的信息交换,它主要包括人到计算机和计算机到人的 信息…...

畅游5G高速网络:联发科集成Wi-Fi6E与蓝牙5.2的系统级单芯片MT7922
这周末,除非外面下钞票,否则谁也拦不住我玩《黑神话悟空》(附:两款可以玩转悟空的显卡推荐) IPBrain平台君 集成电路大数据平台 2024年09月03日 17:28 北京 联发科一直以创新技术追赶市场需求…… “不努力向前游就会被海浪拍回岸边…” 芯片设计公司产品层出不穷,想要站…...

SpringSecurity原理解析(一)
一、SpringSecurity 核心组件 在SpringSecurity中的jar包有4个,作用分别为: spring-security-coreSpringSecurity的核心jar包,认证和授权的核心代码都在这里面spring-security-config如果使用Spring Security XML名称空间进行配置或Spring S…...

在Ubuntu 20.04上安装Nginx的方法
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 简介 Nginx 是世界上最流行的 Web 服务器之一,负责托管互联网上一些最大和流量最高的网站。它是一个轻量级选择,…...

基于苹果Vision Pro的AI NeRF方案:MetalSplatter
随着苹果Vision Pro的发布,混合现实(Mixed Reality, MR)技术迎来了一个新的发展阶段。为了充分利用Vision Pro的潜力,一款名为MetalSplatter的Swift/Metal库应运而生,它允许开发者在Vision Pro上以全立体的方式体验捕捉内容。本文将详细介绍MetalSplatter的特点及其如何为…...

linux系统中,计算两个文件的相对路径
realpath --relative-to/home/itheima/smartnic/smartinc/blocks/ruby/seanet_diamond/tb/parser/test_parser_top /home/itheima/smartnic/smartinc/corundum/fpga/lib/eth/lib/axis/rtl/axis_fifo.v 检验方式就是直接在当前路径下,把输出的路径复制一份࿰…...

[数据集][目标检测]抽烟检测数据集VOC+YOLO格式22559张2类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):22559 标注数量(xml文件个数):22559 标注数量(txt文件个数):22559 标…...
C和指针:结构体(struct)和联合(union)
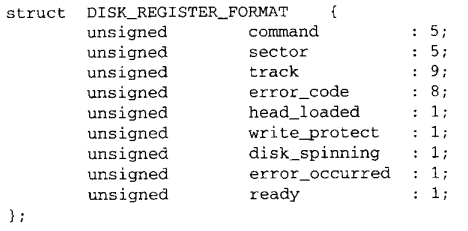
结构体和联合 结构体 结构体包含一些数据成员,每个成员可能具有不同的类型。 数组的元素长度相同,可以通过下标访问(转换为指针)。但是结构体的成员可能长度不同,所以不能用下标来访问它们。成员有自己的名字,可以通过名字访问…...

[数据集][目标检测]电动车头盔佩戴检测数据集VOC+YOLO格式4235张5类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):4235 标注数量(xml文件个数):4235 标注数量(txt文件个数):4235 标注…...

软件工程知识点总结(2):需求分析(一)——用例建模
1 软件项目开发流程: 需求分析→概要设计→详细设计→编码实施→测试→产品提 交→维护 2 系统必须做什么? 获取用户需求,从用户角度考虑,用户需要系统必须完成哪些工作,也就是对目 标系统提出完整、准确、清晰、具体…...

2024 年高教社杯全国大学生数学建模竞赛C题—农作物的种植策略(讲解+代码+成品论文助攻,均已更新完毕)
2024数学建模国赛选题建议团队助攻资料-CSDN博客文章浏览阅读1k次,点赞20次,收藏24次。通过分析5个题目的特点,可知数学建模常用的模型大概可以分为五大类——https://blog.csdn.net/qq_41489047/article/details/141925859 本次国赛white学长…...

?.操作符是什么
?.操作符在不同的编程语言和上下文中可能有不同的含义和用途,但一般来说,它并不是一个广泛存在于所有编程语言中的标准操作符。不过,基于一些编程语言的特性和习惯,我们可以对?.操作符进行一些推测和解释。 1. 可选链操作符&am…...

ArcGIS出图格网小数位数设置
1、比如要去掉格网后面的小数点,如何设置呢? 2、如下图设置。...
)
数学建模_缺失值处理_拉格朗日、牛顿插值(全)
- 缺失值处理 1. 识别缺失值 在处理缺失值之前,首先需要识别数据中的缺失值。 1.1 使用 isna() 和 isnull() Pandas 提供了 isna() 和 isnull() 方法来检测缺失值,二者功能相同。 import pandas as pddf pd.DataFrame({A: [1, 2, None, 4],B: [None, 2,…...
算法题之水壶问题
水壶问题 有两个水壶,容量分别为 x 和 y 升。水的供应是无限的。确定是否有可能使用这两个壶准确得到 target 升。 你可以: 装满任意一个水壶清空任意一个水壶将水从一个水壶倒入另一个水壶,直到接水壶已满,或倒水壶已空。 示…...

Java项目: 基于SpringBoot+mysql蜗牛兼职网兼职平台管理系统(含源码+数据库+答辩PPT+毕业论文)
一、项目简介 本项目是一套基于SpringBootmysql蜗牛兼职网兼职平台管理系统 包含:项目源码、数据库脚本等,该项目附带全部源码可作为毕设使用。 项目都经过严格调试,eclipse或者idea 确保可以运行! 该系统功能完善、界面美观、操…...
, GetLength())
C#数组中的Rank,GetUpperBound(), GetLength()
Rank-数组的秩,一维数组的Rank1;二维数组的Rank2; GetUpperBound()--获取每一维的索引的上限, 比如int[4,5], 那么GetUpperBound(0) 3; GetUpperBound(1) 4 ; 所以 对于二维数组来说 GetUpperBound(0)1行数; G…...

Android应用开发项目式教程——序
文章目录 Android技术本书特点本书内容本书参考 Android技术 Android是重要的客户端技术,因其开源开放的特点,Android在其初期就迅速成长为智能手机的主流操作系统,近年来更进一步成为智能电视、智能车载终端等智能设备的主流操作系统&#…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
