蓝桥杯 - 求组合数【C(a,b)】+ 卡特兰数
文章目录
- 💬前言
- 885. 求组合数 I C(m,n) 【dp】
- 886 求组合数 II 【数据大小10万级别】 【费马小定理+快速幂+逆元】
- 887. 求组合数 III 【le18级别】 【卢卡斯定理 + 逆元 + 快速幂 】
- 888.求组合数 IV 【没有%p -- 高精度算出准确结果】 【分解质因数 + 高精度乘法 --只用一次高精度提高运行效率】
- 889.满足条件的01序列 【卡特兰数-用法极多!】
💬前言
💡本文以组合数多种写法,按不同数据范围结合不同数论知识的组合数末班
组合数是高频的数论考点,掌握组合数是必要的!
如果对您有帮助的话还请动动小手 点赞👍,收藏⭐️,关注❤️
组合数公式:百度文库链接

885. 求组合数 I C(m,n) 【dp】
题目描述 :
给定 n 组询问,每组询问给定两个整数 a,b,请你输出 C(b,a) mod (109+7) 的值。
数据范围 :
1 ≤ n≤10000,
1 ≤ b ≤ a ≤ 2000 【审题C(b,a) a >= b】
输入输出格式 :
输入
第一行包含整数 n。
接下来 n 行,每行包含一组 a 和 b。
输出
共 n 行,每行输出一个询问的解。
输入输出样例 :
输入
3
3 1
5 3
2 2
输出
3
10
1
思路:DP递推式预处理 C(a,b)
C(a,b) = C(a-1,b) + C(a-1,b-1)
选苹果 - 分类 – 每个包含/不包含
【到a的情况对一个未选择的苹果有两种结果,第a个选它,或不选它,选其他的(那么就要从它之外的再选一个)】
[离散数学-接近实际问题-离散-高等代数 - 数学分析 - 均需三学期 !!!]
const int N = 2010 , mod = 1e9 + 7;
int c[N][N];void init()
{for(int i = 0;i < N;i ++)for(int j = 0;j <= i;j ++)if(!j) c[i][j] = 1; //定义: C(a,0) = 1 else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1] % mod); //DP 选/不选
} int main()
{init();int n;scanf("%d",&n);while(n --){int a,b;scanf("%d%d",&a,&b);printf("%d\n",c[a][b]);}return 0;
}886 求组合数 II 【数据大小10万级别】 【费马小定理+快速幂+逆元】
题目描述:
给定n组询问,每组询问给定两个整数a,b,请你输出C(a,b) mod (10^9+7)的值。
输入格式
第一行包含整数n。接下来n行,每行包含一组a和b。
输出格式
共n行,每行输出一个询问的解。
数据范围
1≤n≤100000,1≤b≤a≤105
输入样例:
3
3 1
5 3
2 2
输出样例:
3
10
1
思路: 【即C(a,b)[a>=b]组合公式展开 —> C(a-1,b) * C(a-1,b-1) ,分别求分母和分子】
结合代码:
fact[i] = i! % p;
infact[i] = (i!)的逆元 % p 【除 ==> 乘逆元(快速幂 – 费马小定理)】 【分母 】
C( a , b ) % p = fact[a % p] % p * infact[b - a] % p * infact[b] % p
Cab=a!b!(a−b)!C^b_a = \dfrac{a!}{b!(a-b)!} Cab=b!(a−b)!a!
typedef long long LL;
const int N = 100010,mod = 1e9 + 7;int fact[N],infact[N]; //i! :阶乘 , i阶乘的逆元 : infact[i]int qmi(int a,int k,int p) //数值大就LL 一般都是!!!
{int res = 1; //乘除法的初始值 while(k){if(k % 2) res = (LL)res * a % p; //强转 也可以k & 1 表示奇数就行 a = (LL)a * a % p;k >>= 1;}return res;
}int main()
{fact[0] = infact[0] = 1; //乘除法的初始值 for(int i = 1;i < N;i++){fact[i] = (LL)fact[i - 1] * i % mod;//i的阶乘 infact[i] = (LL)infact[i - 1] * qmi(i,mod - 2,mod) % mod; //a % p 的逆元 的幂 = p-2 ,a逆为a^p-2^ }int n;scanf("%d",&n);while(n --){int a,b;scanf("%d%d",&a,&b);printf("%d\n",(LL)fact[a] * infact[b] % mod * infact[a - b] % mod); //%f等于0原因分母求解过程中0,后一直为0,最后相乘结果为0 }return 0;
}887. 求组合数 III 【le18级别】 【卢卡斯定理 + 逆元 + 快速幂 】
给定n组询问,每组询问给定三个整数a,b,p,其中p是质数,请你输出C b上a下 mod p的值。
输入格式
第一行包含整数n。
接下来n行,每行包含一组a,b,p。
输出格式
共n行,每行输出一个询问的解。
数据范围
1≤n≤20,
1≤b≤a≤1e18,
1≤p≤105,
输入样例:
3
5 3 7
3 1 5
6 4 13
输出样例:
3
3
2
解题思路:
a和b的取值到了1018 改用:
卢卡斯定理: C ( a , b ) % p = C( a%p , b%p ) * C( a/p , b/p ) % p ; (p为质数)
#include<algorithm>typedef long long LL;
int p;int qmi(int a,int k) //p是全局变量不用传进来,直接用
{int res = 1;while(k){if(k % 2) res = (LL)res * a % p;a = (LL)a * a % p; k >>= 1;}return res;
}
//特别注意题目给定输入的a,b顺序
int C(int a,int b) //组合数 C(a,b) == b! / (a-b)! * a! ********
{int res = 1;for(int i = 1,j = a ;i <= b;i++,j--) // i为b! ,j = a! ,qmi求i逆元 为 {res = (LL)res * j % p; //除 , 乘上i的逆元 res = (LL)res * qmi(i,p-2) % p; }return res;
}int lucas(LL a,LL b) //递归 //传进的数是LL类型
{if(a < p && b < p) return C(a,b);return (LL)C(a % p,b % p) * lucas(a / p, b / p) % p;
}int main()
{int n;cin >> n;while(n --){LL a, b;cin >> a >> b >> p ;cout << lucas(a,b) << endl; }
}
888.求组合数 IV 【没有%p – 高精度算出准确结果】 【分解质因数 + 高精度乘法 --只用一次高精度提高运行效率】
较难
题目描述:
输入a,b,求C(a,b)的值。注意结果可能很大,需要使用高精度计算。 【a >= b】
输入格式
共一行,包含两个整数a和b。
输出格式
共一行,输出C(a,b)的值。
数据范围
1≤b≤a≤5000
输入样例:
5 3
输出样例:
10
*公式:C(a,b) = a! / ( b! (a - b)! ) 【a >= b】
一般的处理方式:先把C(a,b)分解质因数,变成只有乘法的形式 --只要高精度乘法 -优化运算速度
质因子p个数运算: 分母里面的有多少个p, - 分子里的多少个p ,差值就是个数
阶乘当中包含p的个数 a! = 向下取整a/p1 [p1为p的倍数] +向下取整a/p2 [p2为p2的倍数] +向下取整a/p3 + …
质数的次数【p的各种倍数中拿出一个p 得出所有含有p的项中,p的总个数】【如p的k次方被加k次,不重复不漏算 】
#include<vector>
const int N = 5010;int primes[N],cnt;
bool st[N];
int sum[N];void get_primes(int n) //线性筛法
{for(int i = 2;i <= n;i++){if(!st[i]) primes[cnt ++] = i;//没有标记,需遍历i的质数的倍数 ,筛除 [第一次i为2,是质数先放入,后面3,5同理,4就被筛掉了]for(int j = 0 ;primes[j] <= n / i;j++) //遍历到 i == sqrt(n) {st[primes[j] * i] = true; //筛除i的质数的倍数, if(i % primes[j] == 0) break; // i是pj 的倍数时,后面已经筛选完了,都是倍数,就不用继续了,结束 }}
}int get(int n,int p) //质因数n的个数
{int res = 0;while(n){res += n / p;n /= p;}return res;
}vector<int> mul(vector<int> a,int b)
{vector<int> c;int t = 0;for(int i = 0;i < a.size();i++){t += a[i] * b;c.push_back(t % 10);t /= 10;}while(t)//t == 0结束 {c.push_back( t % 10);t /= 10; } return c;
}int main()
{int a,b;cin >> a >> b;get_primes(a);for(int i = 0;i < cnt;i++){int p = primes[i];sum[i] = get(a,p) - get(b,p) - get(a - b,p);}vector<int> res;res.push_back(1); for(int i = 0;i < cnt;i++) // 组合数公式== 质因数*对应次幂 for(int j = 0;j < sum[i];j++)res = mul(res,primes[i]); // (res = 1) * primes[i] 的^sum[i]^次方 for(int i = res.size() - 1;i >= 0;i --) printf("%d", res[i]);//vector遍历输出puts("");return 0;
}
889.满足条件的01序列 【卡特兰数-用法极多!】
题目描述:
给定n个0和n个1,它们将按照某种顺序排成长度为2n的序列,求它们能排列成的所有序列中,
能够满足任意前缀序列中0的个数都不少于1的个数的序列有多少个。输出的答案对10^9+7取模。
输出格式
共一行,包含整数n。
输出格式
共一行,包含一个整数,表示答案。
数据范围
1≤n≤105
输入样例:
3
输出样例:
5
思路
路径转换成一个排列 ,如坐标从(0,0)开始走,0向右走,1向上走,到终点得到一个序列
当要求能走的坐标满足x >= y 时,ans = = 即所有不经过y = x + 1这条边的数 = = 所有走法 - 经过y = x + 1这条边的数
如(0,0)- - >(6,6) 必走12步且选6步向上走 y = x + 1等效,即C(12,6) - C(12,5)
扩展推: (0,0) 到 (n,n) 且不经过y = x + 1 即
Cat(n) = C(n+n , n) - C(n+n , n-1) = C(2*n,n) / (n + 1) 【卡特兰数】
【卡特兰数应用:栈的合法序列,括号匹配数量…
简记: qmi(x的逆元) ,在%p条件下可以表示为 1 / x
main :
①②求C(2n,n) ①先求 a! / (a-b)! for(int i = a;i > a - b;i --) res = (LL)res * i % mod; //a! / (a-b)!②再求 1 / b! for(int i = 1;i <= b;i ++) res = (LL)res * qmi(i,mod - 2,mod) % mod; ③最后再乘 1 / (n+1) 【用 n+1 的逆元表示】res = (LL)res * qmi(n + 1,mod - 2,mod) % mod;
#include<bits/stdc++.h>
using namespace std;typedef long long LL;
const int mod = 1e9 + 7;//取模为质数
//因为%p所以都可以int
ll qmi(int a,int k,int p) //如果p不是质数,那么逆元只能用扩展欧几里得定理求!!!
{int res = 1;while(k){if(k % 2) res = (LL)res * a % p;a = (LL)a * a % p;k >>= 1; }return res;
}int main()
{int n;cin >> n;int a = 2 * n , b = n; int res = 1;//求C(2*n,n) = a! / b!(a-b)! 【C(a,a-b) * b!逆元(分母)】for(int i = a;i > a - b;i --) res = (LL)res * i % mod; //a! / (a-b)!for(int i = 1;i <= b;i ++) res = (LL)res * qmi(i,mod - 2,mod) % mod; //C(2*n,n) / (n+1)res = (LL)res * qmi(n + 1,mod - 2,mod) % mod; // 乘(n+1) 逆元 == 1/(n+1) % pcout << res << endl;return 0;
}
一篇不同代码的卡特兰数01序列
【其他代码-dp法参考】
卡特兰数 : Cat(n)=C2nn(n+1)Cat(n) = \frac{C_{2n}^n}{(n + 1)}Cat(n)=(n+1)C2nn
带入试试是否满足样例!
卡特兰数的简单代码实现 【DP】
组合数dp法求卡特兰数
c[a][b]仅能求 1 <= a,b <= 2000
Cat(n)=C2nn−C2nn−1=C2nnn+1Cat(n)= {C_{2n}^n} - {C_{2n}^{n-1}} = \dfrac{C_{2n}^n}{n+1} Cat(n)=C2nn−C2nn−1=n+1C2nn
const int N = 1e4+10;
int c[N][N]; //存组合数 c[a][b] 表示从a个苹果中选b个的方案数 【a >= b】void init() //init数组,组合数
{
for (int i = 0; i < N; i ++ )for (int j = 0; j <= i; j ++ )if (!j) c[i][j] = 1;else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod; //逆推,取第b个时是最后一个还是前面的(最后一个取/不取) }int main()
{cin >> n;cout << c[2*n][n] / (n+1) ;return 0;
}
分解质因数法求组合数 —— 模板题 AcWing 888. 求组合数 IV
当我们需要求出组合数的真实值,而非对某个数的余数时,分解质因数的方式比较好用:
1. 筛法求出范围内的所有质数
2. 通过 C(a, b) = a! / b! / (a - b)! 这个公式求出每个质因子的次数。 n! 中p的次数是 n / p + n / p^2 + n / p^3 + …
3. 用高精度乘法将所有质因子相乘
相关文章:

蓝桥杯 - 求组合数【C(a,b)】+ 卡特兰数
文章目录💬前言885. 求组合数 I C(m,n) 【dp】886 求组合数 II 【数据大小10万级别】 【费马小定理快速幂逆元】887. 求组合数 III 【le18级别】 【卢卡斯定理 逆元 快速幂 】888.求组合数 IV 【没有%p -- 高精度算出准确结果】 【分解质因数 高精度乘法 --只用一…...

膳食真菌在癌症免疫治疗中的作用: 从肠道微生物群的角度
谷禾健康 癌症是一种恶性肿瘤,它可以发生在人体的任何部位,包括肺、乳房、结肠、胃、肝、宫颈等。根据世界卫生组织的数据,全球每年有超过1800万人被诊断出患有癌症,其中约有1000万人死于癌症。癌症已成为全球范围内的主要健康问题…...

怎么将模糊的照片变清晰
怎么将模糊的照片变清晰?珍贵的照片每个人都会有,而遇到珍贵的照片变模糊了,相信会让人很苦恼的。那么有没有办法可以解决呢?答案是有的,我们可以用工具让模糊的照片变得清晰。下面就来分享一些让模糊的照片变清晰的方法,有兴趣…...
【软件测试】基础知识第一篇
文章目录一. 什么是软件测试二. 测试和调试的区别三. 什么是测试用例四. 软件的生命周期五. 软件测试的生命周期一. 什么是软件测试 软件测试就是验证软件产品特性是否满足用户的需求。 那需求又是什么呢?在多数软件公司,会有两种需求,一种…...

【百面成神】java web基础7问,你能坚持到第几问
前 言 🍉 作者简介:半旧518,长跑型选手,立志坚持写10年博客,专注于java后端 ☕专栏简介:纯手打总结面试题,自用备用 🌰 文章简介:java web最基础、重要的8道面试题 文章目…...

Centos7安装、各种环境配置和常见bug解决方案,保姆级教程(更新中)
文章目录前言一、Centos7安装二、各种环境配置与安装2.1 安装net-tools(建议)2.2 配置静态网络(建议)2.1 修改Centos7的时间(建议)2.2 Centos7系统编码问题2.3 vim安装(建议)2.4 解决…...

【C++进阶】智能指针
文章目录为什么需要智能指针?内存泄漏什么是内存泄漏,内存泄漏的危害内存泄漏分类(了解)如何避免内存泄漏智能指针的使用及原理smart_ptrauto_ptrunique_ptrshared_ptr线程安全的解决循环引用weak_ptr删除器为什么需要智能指针&am…...

软件测试面试题 —— 整理与解析(3)
😏作者简介:博主是一位测试管理者,同时也是一名对外企业兼职讲师。 📡主页地址:🌎【Austin_zhai】🌏 🙆目的与景愿:旨在于能帮助更多的测试行业人员提升软硬技能…...

springboot常用的20个注解
Spring Boot方式的项目开发已经逐步成为Java应用开发领域的主流框架,它不仅可以方便地创建生产级的Spring应用程序,还能轻松地通过一些注解配置与目前比较火热的微服务框架SpringCloud集成, 而Spring Boot 之所以能够轻松地实现应的创建及与…...

USB组合设备——带鼠标功能的键盘
文章目录带鼠标功能的键盘一个接口实现报告描述符示例多个接口实现复合设备和组合设备配置描述符集合的实现报告的返回附 STM32 枚举日志复合设备:Compound Device 内嵌 Hub 和多个 Function,每个 Function 都相当于一个独立的 USB 外设,有自…...
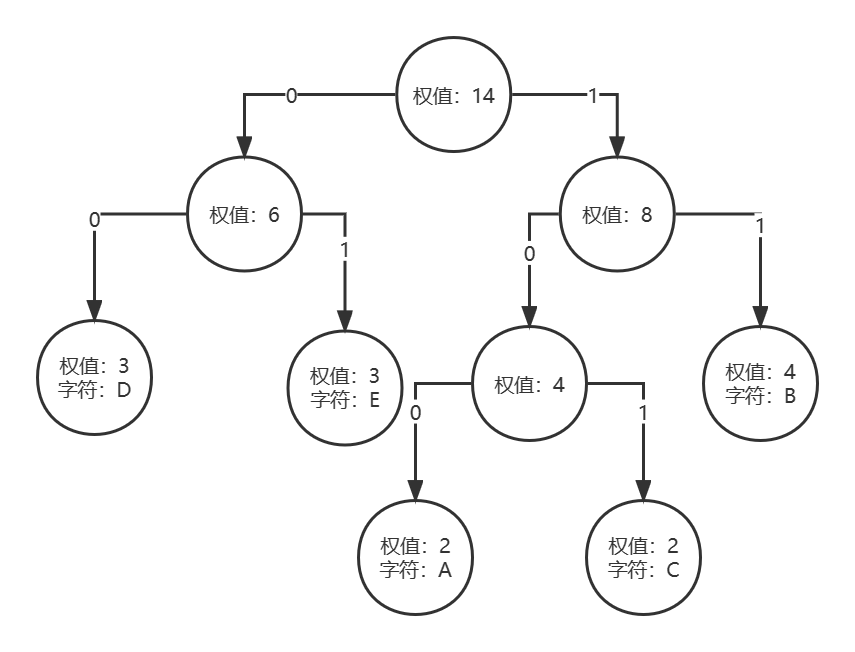
数据结构与算法基础-学习-18-哈夫曼编码
一、个人理解在远程通讯中,需要把字符转成二进制的字符串进行传输,例如我们需要传输ABCD,我们可以用定长的字符串进行表示,例如:A:00B:01C:02D:03这样可能就造成空间的浪费,我们多存储了一个0号位。那用变长呢…...

ZMC408CE | 实现“8通道独立PSO”应用场景
一、ZMC408SCAN产品亮点 1.高性能处理器,提升运算速度、响应时间和扫描周期等; 2.一维/二维/三维、多通道视觉飞拍,高速高精; 3.位置同步输出PSO,连续轨迹加工中对精密点胶胶量控制和激光能量控制等; 4…...

QuickJS中JS_SetClassProto方法把JavaScript对象指定为某个类的原型对象
在 QuickJS 中,JS_SetClassProto 方法用于设置一个类的原型对象。这个方法的作用是将一个 JavaScript 对象指定为该类的原型对象,从而定义该类的属性和方法。 具体来说,JS_SetClassProto 方法的第一个参数是指向 QuickJS 引擎执行上下文的指…...

泰克信号发生器特点
泰克信号发生器是一种用于产生各种类型的电子信号的仪器,可以广泛应用于电子、通信、自动化、医疗等领域。泰克信号发生器具有以下特点:多种信号类型:泰克信号发生器可以产生多种类型的电子信号,包括正弦波、方波、三角波、脉冲等…...

贯穿设计模式第四话--里氏替换原则
🥳🥳🥳 茫茫人海千千万万,感谢这一刻你看到了我的文章,感谢观赏,大家好呀,我是最爱吃鱼罐头,大家可以叫鱼罐头呦~🥳🥳🥳 从今天开始,将…...

6501: 鸡兔同笼
描述 一个笼子里面关了鸡和免子(鸡有两只脚,兔子有4只脚,没有例外)。已经知道了笼子里面脚的总数a,问笼子里面至少有多少只动物,至多有多少只动物。 输入 一个正整数a(a<32768)。 输出 包含两个正整数,第一个是最少的动物数,第二个是最多的…...

Linux项目自动化构建工具-make/makefile 介绍及使用
使用背景 在工程中的源文件不计数,其按类型、功能、模块分别放在若干个目录中,makefile定义一系列 规则来指定什么文件需要先编译,什么文件需要后编译,哪些文件需要重新编译,或者更复杂 的功能操作 makefile带来的好处…...

【云原生|Docker】06-dokcerfile详解
目录 前言 Dockerfile基础示例 Dockerfile简介 1. Dockerfile概念 2. Dokcer镜像分层理解 3. Doker build构建原理 Dockerfile参数解析 1. Dokcerfile组成 2. 指令说明 2.1 FROM引入基础镜像 2.2 LABEL 2.3 ENV 2.4 RUN 2.5 COPY 2.6 ADD 2…...
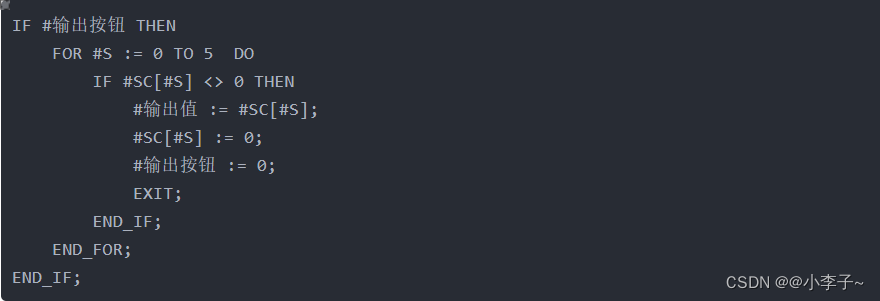
【SCL】博图——先入先出排序法
使用博图SCL语言来实现先入先出排序 前言 使用SCL完成一个先入先出排序 具体要求:最先输入的一个数值,最先输出出来,下面的数自动向前填充; 注:这里可能有两种理解:一是第一个输入的第一个出来ÿ…...
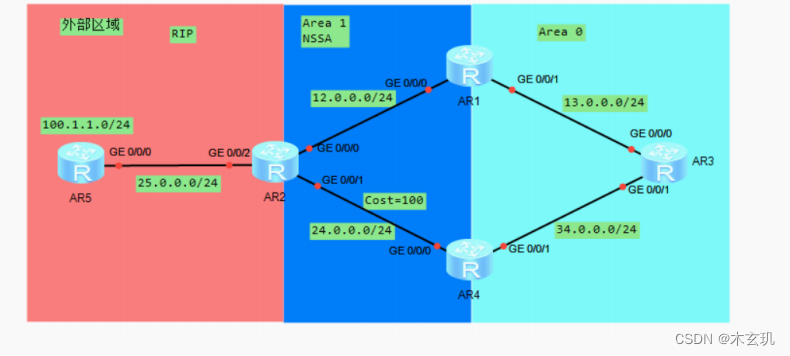
OSPF----特殊区域
目录 OSPF----特殊区域 第一大类----末梢区域(Stub Area) 完全末梢区域((Totally Stub Area) 第二大类特殊区域----非完全末梢区域(NSSA) OSPF----特殊区域 第一大类----末梢区域(Stub Area)…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
