C语言手撕实战代码_二叉排序树(二叉搜索树)_构建_删除_插入操作详解
| 二叉排序树习题 |
|---|
| 1.设计算法构建一棵二叉排序树(又称二叉搜索树BST) |
| 2.查找二叉排序树中结点为x的结点所在的层数 |
| 3.删除二叉排序树T中值为x的结点 |
| 4.查找二叉排序树中所有小于key的关键字 |
| 5.编写算法,将一棵二叉树t分解成两棵二叉排序树t1和t2,使得t1中的所有结点关键字的值都小于x,t2中所有结点关键字的值都大于x |
| 6.已知二叉排序树中每一个结点值为整型,采用二叉链表存储,编写算法删除二叉排序树中所有关键字小于x的结点 |
文章目录
- 1.设计算法构建一棵二叉排序树(又称二叉搜索树BST)
- 2.查找二叉排序树中结点为x的结点所在的层数
- 3.删除二叉排序树T中值为x的结点
- 4.查找二叉排序树中所有小于key的关键字
- 5.编写算法,将一棵二叉树t分解成两棵二叉排序树t1和t2,使得t1中的所有结点关键字的值都小于x,t2中所有结点关键字的值都大于x
- 6.已知二叉排序树中每一个结点值为整型,采用二叉链表存储,编写算法删除二叉排序树中所有关键字小于x的结点
1.设计算法构建一棵二叉排序树(又称二叉搜索树BST)
二叉树搜索树的构建就是多个插入操作的重复使用,下面的代码并用二叉树的前序遍历检验插入结果。
二叉排序树,中序序列序列就变成了有序输出
#include <stdio.h>
#include <stdlib.h>typedef int ElemType;
typedef struct BiTNode
{ElemType data;struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;//二叉排序树的插入操作
void insertKey(BiTree &T,ElemType key)
{//if是根(子树根)节点的操作,else if是左右子树操作 根节点+左右子树的操作=问题的解if(T==NULL){BiTNode * p=(BiTNode *)malloc(sizeof(BiTNode));p->lchild=NULL;p->rchild=NULL;p->data=key;T=p;}else if(key<T->data)//如果key<当前结点{insertKey(T->lchild, key);}else if(key >T->data){insertKey(T->rchild, key);}
}BiTNode * creatBSTree()
{BiTNode *T=NULL;ElemType keyList[]={40,10,45,15};int keyListLength=4;for(int i=0;i<keyListLength;i++){insertKey(T, keyList[i]);}return T;
}void preOreder(BiTree T)
{if(T==NULL) return;printf("%d ",T->data);preOreder(T->lchild);preOreder(T->rchild);
}
int main()
{BiTree T=creatBSTree();preOreder(T);printf("\n");
}2.查找二叉排序树中结点为x的结点所在的层数
我的思考?在上一节中,我们可以用层序遍历来完成这个事,但是那个是全部二叉树可用,这一次有什么区别
答:之前的二叉树要遍历完全部的结点,才能找到x。需要横着找
这次有序的寻找就不同了,是竖着找
int nodelevel=0;
int getNode(BiTree T,int x)
{if(T!=NULL){nodelevel++;if(x== T->data) return nodelevel;else if(x<T->data){getNode(T->lchild, x);}else if(x>T->data){getNode(T->rchild, x);}}else nodelevel=0;//表明没有查到x,返回0return nodelevel;
}
3.删除二叉排序树T中值为x的结点
找到值为x的结点,然后删除该点

我们这里以方法1为例子,右孩子,插入到左孩子的最大结点中
思路提炼:
关于存在两棵子树的时候,
找到左子树的最右子树(最大结点),它肯定没有右孩子,将待删除结点的右孩子变成它的右孩子,删掉待删除结点即可
void deleteopr(BiTree &T)
{//第一种情况,删除结点是根节点,第二种情况,只有一个子树,第三种情况,有两个子树if(T->lchild==NULL&&T->rchild==NULL){T=NULL;}else if(T->lchild!=NULL&&T->rchild!=NULL){BiTNode *pMax=T->lchild;while(pMax->rchild!=NULL){pMax=pMax->rchild;}pMax->rchild=T->rchild;BiTNode *p=T;T=T->lchild;free(p);}else //只有一边有子树{//如果左边有子树if(T->lchild!=NULL){//记录被抛弃的结点的存储空间,用完它之后就给他free掉BiTNode *p=T;T=T->lchild;free(p);}else{BiTNode *p=T;T=T->rchild;free(p);}}
}
void delete_treeNode(BiTree &T,ElemType x)
{if(T->data==x){//删除这个结点,删除操作开始,否则的话,就继续往左右子树里寻找这个结点deleteopr(T);}else if(x<T->data){delete_treeNode(T->lchild, x);}else if(x>T->data){delete_treeNode(T->rchild, x);}
}4.查找二叉排序树中所有小于key的关键字
思路:二叉排序树中序遍历是有序的,所以在中序遍历的过程中就能找到全部小于key的结点,中止中序遍历就行。
简单代码已省略
5.编写算法,将一棵二叉树t分解成两棵二叉排序树t1和t2,使得t1中的所有结点关键字的值都小于x,t2中所有结点关键字的值都大于x
思路:
6.已知二叉排序树中每一个结点值为整型,采用二叉链表存储,编写算法删除二叉排序树中所有关键字小于x的结点
错误思路:是以为找到某点小于x,就把它连同它的左子树全部删除,若它存在右子树,就让它右子树代替它。这种思路就漏解了,漏掉了小于结点的右子树中,仍可能存在小于x的结点。

明确使用哪种遍历?-使用前序遍历,因为根节点是划分区间的依据,只有使用前序遍历,我们才能够先拿到根结点。

void deleteFunc(BiTree &T) //删除一整棵树,先删除左子树,再删除右子树,最后删除根节点,就不用保存根节点的信息了
{if(T!=NULL){deleteFunc(T->lchild);deleteFunc(T->rchild);free(T);T = NULL; // 避免悬空指针,直接将T设为NULL,已经释放掉的指针}
}void preOrderTraversing(ElemType x,BiTree &T)
{//如果树不为空if(T!=NULL){if(T->data==x) //如果当前正正好好,T的左子树小于x,T的右子树大于x,那么删除左子树即可{//deleteFunc(T->lchild); //删除函数,删除了T的左孩子T->lchild=NULL;}else if(x>T->data) //如果当前x大于该结点,那么该结点的左孩子肯定都比x小,需要删除,右孩子中可能存在着小于x的值,所以右孩子要递归{//递归删除右子树preOrderTraversing(x,T->rchild);//删除左子树和根节点,这里注意删除根节点的时候,它可能存在右孩子,所以要让指针指向他的右孩子,我们保存根节点信息,直接让指针指向其右孩子BiTNode* p=T;T=T->rchild;p->rchild=NULL; //右子树置空,为什么要把右子树置空,要切断它指针的联系,因为现在的右子树已经是新的根节点了,如果不把老的根节点的右子树置空,删除操作的时候,会把右子树也删除了//deleteFunc(p); //删除根节点和它的左孩子}else if(x<T->data) //如果当前x小于该结点,那么该结点的右孩子肯定都比x大,左孩子中可能存在着小于x的值,所以左孩子要递归{//右子树不用管,处理它的左子树就行preOrderTraversing(x,T->lchild);}}
}
相关文章:

C语言手撕实战代码_二叉排序树(二叉搜索树)_构建_删除_插入操作详解
二叉排序树习题1.设计算法构建一棵二叉排序树(又称二叉搜索树BST)2.查找二叉排序树中结点为x的结点所在的层数3.删除二叉排序树T中值为x的结点4.查找二叉排序树中所有小于key的关键字5.编写算法,将一棵二叉树t分解成两棵二叉排序树t1和t2,使得t1中的所有…...

YC教父的创始人模式VS职业经理人模式:AI时代的独立开发者崛起
近年来,由风投资助的创始人模式因其相对较低的入门门槛而在创业圈内广受欢迎。然而,真正的挑战在于独立开发者(一人商业)模式。随着AI技术的飞速发展,一人商业模式有望成为未来的主流。本文将探讨独立开发者的工作范围…...

[SUCTF 2019]Pythonginx
给了源码 app.route(/getUrl, methods[GET, POST]) def getUrl():url request.args.get("url")host parse.urlparse(url).hostnameif host suctf.cc:return "我扌 your problem? 111"parts list(urlsplit(url))host parts[1]if host suctf.cc:retu…...

省市县相关校验sql随笔
1.层级校验 要判断一个给定的省、市、区(县)名字是否符合正确的层级关系,假设你的表结构如下: CREATE TABLE regions (id INT PRIMARY KEY,name VARCHAR(255),parent_id INT, -- 指向上一级区域的id,例如市的parent_id指向省的…...
消失问题)
uniapp ios sticky定位,内部 u-tabs(包含scroll-view)消失问题
uniapp中用sticky定位时,元素内部如果有scroll-view,ios在触发bounce机制时,scroll-view的元素会消失,解决方法是页面上包一层高度为100vh的scroll-view <scroll-view style"height: 100vh;" scroll-y scrolltolowe…...

web群集--nginx配置文件location匹配符的优先级顺序详解及验证
文章目录 前言优先级顺序优先级顺序(详解)1. 精确匹配(Exact Match)2. 正则表达式匹配(Regex Match)3. 前缀匹配(Prefix Match) 匹配规则的综合应用验证优先级 前言 location的作用 在 NGINX 中࿰…...

Vivado编译报错黑盒子问题
1 问题描述 “Black Box Instances: Cell **** of type ** has undefined contents and is considered a back box. The contents of this cell must be defined for opt_design to complete successfully.” 检查工程代码提示的模块,该模块为纯手写的Veril…...

【建造者模式】
建造者模式 Builder Pattern 属于创建型模式是将一个复杂对象的构建与它的标识分离,使得同样的构建过程可以创建不同的表示关键点:用户只需要指定需要建造的类型就可以获得对象,建造过程及细节不需要了解 实现 demo 需要构建的对象 Data pu…...
自动化表格处理的革命:智能文档系统技术解析
在当今数据驱动的商业环境中,表格数据的自动化处理成为了企业提高效率、降低成本的关键。企业智能文档系统在智能表格识别方面展现出卓越的性能,通过精准识别和处理各种通用表格,显著提升了企业文档管理的智能化水平。本文将深入探讨该系统在…...

【Hot100】LeetCode—394. 字符串解码
目录 1- 思路栈实现四种情况处理 2- 实现⭐394. 字符串解码——题解思路 3- ACM 实现 原题链接:394. 字符串解码 1- 思路 栈实现四种情况处理 ① 遇到数字,进行倍数相加 、②遇到左括号,压栈之前的元素、③遇到右括号弹出,栈进行…...

12. 如何在MyBatis中进行分页查询?常见的分页实现方式有哪些?
在MyBatis中,分页查询是一种常见的需求,尤其是在处理大数据量的情况下。MyBatis本身不直接提供分页功能,但可以通过以下几种常见的实现方式来实现分页查询。 1. 手动分页 这是最基本的分页方式,直接在SQL语句中添加分页参数。不同…...
)
@[TOC](力扣题目-滑动窗口-qsort排序-二分法查找)
通信 LCR 009. 乘积小于 K 的子数组268. 丢失的数字287. 寻找重复数 LCR 009. 乘积小于 K 的子数组 已解答 滑动窗口 给定一个正整数数组 nums和整数 k ,请找出该数组内乘积小于 k 的连续的子数组的个数。 示例 1: 输入: nums [10,5,2,6], k 100 输出: 8 解释…...

Docker容器相关命令
Docker是一种容器化技术,可以帮助用户更轻松地创建、部署和管理容器。下面是一些常见的Docker容器管理任务: 创建容器:使用Docker镜像创建一个新的容器。 docker run image_name列出容器:查看当前运行的容器列表。 docker ps启动容…...

【老课推荐】基于LangChain和知识图谱的大模型医疗问答机器人项目
在当今数据驱动和人工智能主导的时代,大模型和知识图谱的结合是一个重要的研究和应用方向。大模型实战课程通过48课时,分为六个主要章节,涵盖了从基本概念到高级应用的多方面内容。学员将通过本课程学习如何使用LangChain和OpenAI进行开发&am…...

Adobe Sensei——自动化视频编辑、特效应用和素材增强,通过AI技术快速优化视频内容,自动修复视频质量、自动添加背景音乐或字幕
一、Adobe Sensei介绍 Adobe Sensei 是 Adobe 公司开发的一款基于人工智能和机器学习技术的平台,旨在增强其各种创意、文档和体验管理工具。Adobe Sensei 通过深度学习、计算机视觉、自然语言处理(NLP)等先进技术,帮助用户在 Ado…...

【AIGC数字人】EchoMimic:基于可编辑关键点条件的类人音频驱动肖像动画
GitHub:https://github.com/BadToBest/EchoMimic 论文: https://arxiv.org/pdf/2407.08136 comfyui: https://github.com/smthemex/ComfyUI_EchoMimic 相关工作 Wav2Lip Wav2Lip是一个开创性的工作 ,但输出会出现面部模糊或扭…...

变量数据类型 Day3
1. 变量 1.1 变量的概念 变量是计算机内存中的一块存储单元,是存储数据的基本单元变量的组成包括:数据类型、变量名、值,后文会具体描述变量的本质作用就是去记录数据的,比如说记录一个人的身高、体重、年龄,就需要去…...

SpringBoot2:请求处理原理分析-RESTFUL风格接口
一、RESTFUL简介 Rest风格支持(使用HTTP请求方式,动词来表示对资源的操作) 以前:/getUser 获取用户 /deleteUser 删除用户 /editUser 修改用户 /saveUser 保存用户 现在: /user GET-获取用户 DELETE-删除用户 PUT-修改…...

[Linux][配置]Linux修改history存储的最大记录数
Linux修改History最大记录为20000行 sed -i s/^HISTSIZE1000/HISTSIZE20000/ /etc/profile source /etc/profile 在 Linux 系统中,HISTSIZE 环境变量用于定义历史记录的大小,即在终端中可以回溯的命令数量。默认情况下,这个值通常是 1000&…...
代码随想录 刷题记录-28 图论 (5)最短路径
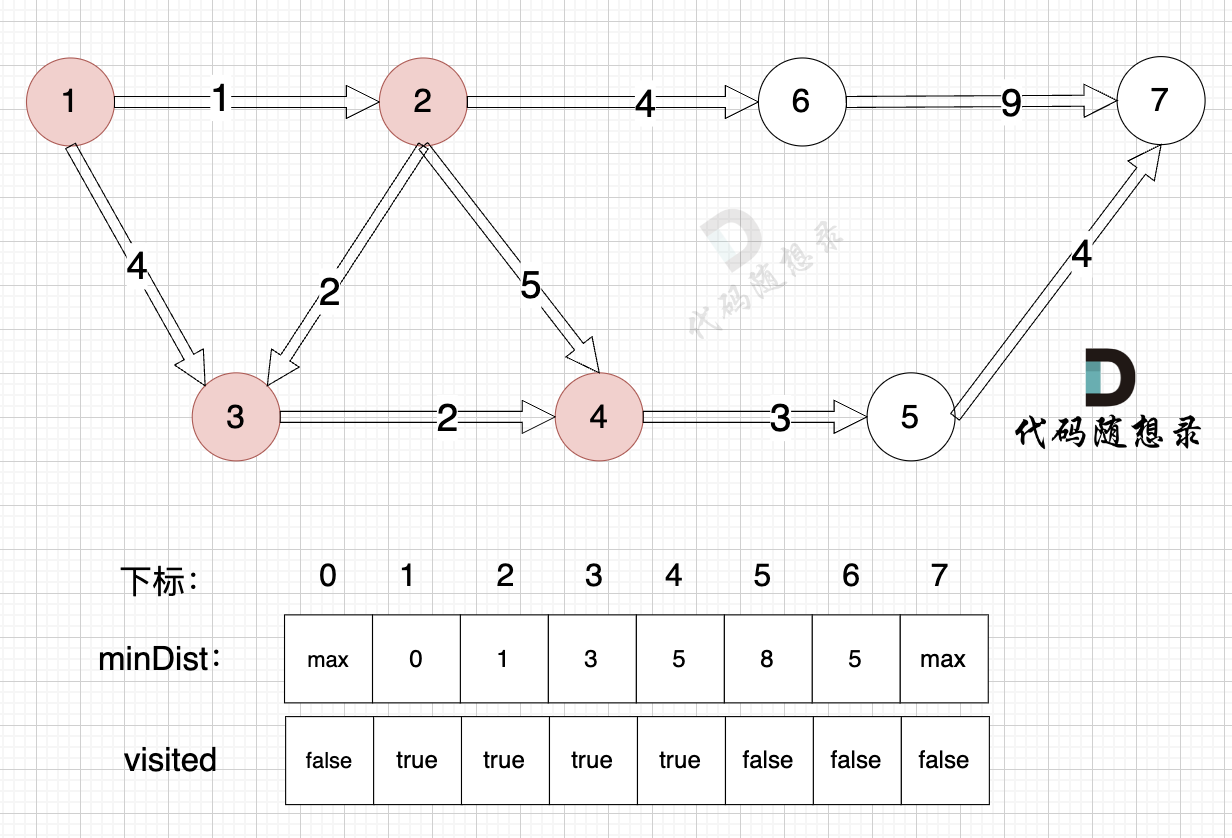
一、dijkstra(朴素版)精讲 47. 参加科学大会 思路 本题就是求最短路,最短路是图论中的经典问题即:给出一个有向图,一个起点,一个终点,问起点到终点的最短路径。 接下来讲解最短路算法中的 d…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...
