MSCKF7讲:特征管理与优化
MSCKF7讲:特征管理与优化
文章目录
- MSCKF7讲:特征管理与优化
- 1 Feature.h
- 2 OptimizationConfig
- 3 initializePosition三角化+LM优化
- 3.1 计算归一化坐标深度初值generateInitialGuess
- ① 理论推导
- ② 代码分析
- 3.2 计算归一化误差cost
- ① 理论推导
- ② 代码分析
- 3.3 计算雅可比jacobian()
- ① 理论推导
- ② 代码分析
- 3.4 计算视差checkMotion—能否三角化
- ① 理论分析
- ② 代码分析
- 3.5 初始化Position
- 4 特征管理总结
- 4.1 特征投影
- 4.2 特征参数
- 4.2.1 基于坐标系划分
- 4.2.2 基于XYZ或者逆深度
- XYZ
- 逆深度1:球坐标逆深度
- 逆深度2:MSCKF逆深度
- 4.3 MSCKF逆深度
- 4.4 VINS逆深度
写在前面,MSCKF里面维度一个feature.hpp,用来管理特征
std::map<StateIDType, Eigen::Vector4d, std::less<StateIDType>,Eigen::aligned_allocator<std::pair<const StateIDType, Eigen::Vector4d>>>observations; // 存放了观测到当前特征(路标点)的所有帧id,以及对应坐标系下的归一化坐标,因为这里是双目相机,所以是Vector4d// 3d postion of the feature in the world frame.
Eigen::Vector3d position;
msckf是一个vio系统,他不会对路标点进行优化更新,也不关注全局map,不会保存地图信息,只会把要删除的点去做更新,所以下面MapServer中只是保存了一段时间的特征(路标点)
// 地图----特征(路标点)管理
typedef Feature::FeatureIDType FeatureIDType; // int
typedef std::map<FeatureIDType, Feature, std::less<int>, // 存储了特征的map容器Eigen::aligned_allocator<std::pair<const FeatureIDType, Feature>>>MapServer;
| 状态量 | 含义 |
|---|---|
MapServer | 存储满足要求的特征点,键-特征id,值-对应特征(路标点) |
FeatureIDType | 长整型long long int |
Feature | 特征结构体,描述一个路标点应该有的东西 |
MSCKF中特征参数使用了逆深度的形式,即 λ = [ α β ρ ] ⊤ \boldsymbol{\lambda}=\begin{bmatrix}\alpha&\beta&\rho\end{bmatrix}^{\top} λ=[αβρ]⊤。(X/Z, Y/Z, 1/Z)
使用逆深度
好处:能够表示无穷远点,当特征点较远时, z 数值比较大,直接估计 z 会存在数值问题
坏处:当z趋于0时,ρ趋于无穷大,存在数值奇异,只能用在相机坐标系中,因为相机系下坐标深度都是大于0的,不会趋于0;特别是在非相机坐标系中,因为在那里点的深度可以是负值或零。
1 Feature.h
记录观测特征(路标点)的类,一个特征对应的一些成员(特征id、三维点坐标)、三角化函数等
/** * @brief Feature Salient part of an image.* 一个特征可以理解为一个三维点,由多帧观测到*/
struct Feature
{EIGEN_MAKE_ALIGNED_OPERATOR_NEWtypedef long long int FeatureIDType;struct OptimizationConfig{}; // 优化参数配置// 构造函数:初始化特征id,空间位置Feature() : id(0), position(Eigen::Vector3d::Zero()),is_initialized(false) {}Feature(const FeatureIDType &new_id): id(new_id),position(Eigen::Vector3d::Zero()),is_initialized(false) {}/*** @brief 计算三维点的重投影误差* @param T_c0_c1 即Tcic0* @param x The current estimation.要投影的三维点* @param z The ith measurement of the feature j in ci frame.观测* @return e The cost of this observation.重投影误差*/inline void cost(const Eigen::Isometry3d &T_c0_ci,const Eigen::Vector3d &x, const Eigen::Vector2d &z,double &e) const;/*** @brief 计算观测z对三维点的雅可比(这里的三维点不是传统意义上的三维点,具体看程序吧)* @param T_c0_c1 即Tcic0* @param x The current estimation.要投影的三维点* @param z 第j个特征在第ci帧中的观测* @return J The computed Jacobian.* @return r The computed residual.残差* @return w Weight induced by huber kernel.高斯核*/inline void jacobian(const Eigen::Isometry3d &T_c0_ci,const Eigen::Vector3d &x, const Eigen::Vector2d &z,Eigen::Matrix<double, 2, 3> &J, Eigen::Vector2d &r,double &w) const;/*** @brief 使用两帧(观测到该点的第一帧(左)核最后一帧(右))去三角化初始的三维点坐标* @param z1: feature observation in c1 frame.* @param z2: feature observation in c2 frame.* @return p: Computed feature position in c1 frame.*/inline void generateInitialGuess(const Eigen::Isometry3d &T_c1_c2, const Eigen::Vector2d &z1,const Eigen::Vector2d &z2, Eigen::Vector3d &p) const;/*** @brief 检验三角化是否合理* @param cam_states : input camera poses.* @return True if the translation between the input camera* poses is sufficient.*/inline bool checkMotion(const CamStateServer &cam_states) const;/*** @brief InitializePosition Intialize the feature position* based on all current available measurements.供外部调用* @param cam_states:std::map<StateIDType, CAMState>* @return The computed 3d position is used to set the position* member variable. Note the resulted position is in world* frame.* @return True if the estimated 3d position of the feature* is valid.*/inline bool initializePosition(const CamStateServer &cam_states);// 特征idFeatureIDType id;// id for next featurestatic FeatureIDType next_id;// 升序排序的map// 键:观测到这个特征点的 帧id// 值:注意这里4表示的是左右相机的特征点对应坐标std::map<StateIDType, Eigen::Vector4d, std::less<StateIDType>,Eigen::aligned_allocator<std::pair<const StateIDType, Eigen::Vector4d>>>observations;// 对应在世界系下的坐标Eigen::Vector3d position;bool is_initialized;// Noise for a normalized feature measurement.static double observation_noise;// Optimization configuration for solving the 3d position.static OptimizationConfig optimization_config;
};
2 OptimizationConfig
主要设置了最小二乘法—列文伯格算法中的参数、平移量阈值等
/** 优化配置* @brief OptimizationConfig Configuration parameters* for 3d feature position optimization.* 优化参数*/
struct OptimizationConfig
{// 位移是否足够,用于判断点是否能做三角化double translation_threshold;// huber参数double huber_epsilon;// 修改量阈值,优化的每次迭代都会有更新量,这个量如果太小则表示与目标值接近double estimation_precision;// LM算法lambda的初始值double initial_damping;// 内外轮最大迭代次数int outer_loop_max_iteration;int inner_loop_max_iteration;OptimizationConfig(): translation_threshold(0.2),huber_epsilon(0.01),estimation_precision(5e-7),initial_damping(1e-3),outer_loop_max_iteration(10),inner_loop_max_iteration(10){return;}
};
3 initializePosition三角化+LM优化
功能:feature主函数,利用观测到的特征点来进行三角化(利用左目不同时刻的帧,第一次观测帧、最后一次观测帧),返回是否三角化成功
/*** @brief initializePosition 三角化+LM优化* @param cam_states 所有参与计算的相机位姿 是一个map容器,键-id 值-相机状态* @return 是否三角化成功*/
bool Feature::initializePosition(const CamStateServer &cam_states)
{// Organize camera poses and feature observations properly.// 存放每个观测以及每个对应相机的pos,注意这块是左右目独立存放std::vector<Eigen::Isometry3d, Eigen::aligned_allocator<Eigen::Isometry3d>> cam_poses(0);std::vector<Eigen::Vector2d, Eigen::aligned_allocator<Eigen::Vector2d>> measurements(0);// 1. 添加每一个观测对应的帧信息(左右双目)for (auto &m : observations){// TODO: This should be handled properly. Normally, the// required camera states should all be available in// the input cam_states buffer.// 找到对应观测到该的特征点的帧auto cam_state_iter = cam_states.find(m.first);if (cam_state_iter == cam_states.end())continue;// Add the measurement.// 1.1 添加归一化坐标measurements.push_back(m.second.head<2>());measurements.push_back(m.second.tail<2>());// This camera pose will take a vector from this camera frame// to the world frame.// TwcEigen::Isometry3d cam0_pose;cam0_pose.linear() =quaternionToRotation(cam_state_iter->second.orientation).transpose();cam0_pose.translation() = cam_state_iter->second.position;Eigen::Isometry3d cam1_pose;cam1_pose = cam0_pose * CAMState::T_cam0_cam1.inverse();// 1.2 添加相机位姿cam_poses.push_back(cam0_pose);cam_poses.push_back(cam1_pose);}// All camera poses should be modified such that it takes a// vector from the first camera frame in the buffer to this// camera frame.// 2. 中心化位姿,提高计算精度---实际上就是把第一帧当基准,找到第一帧到其它帧(包括了右目)的位姿变换Eigen::Isometry3d T_c0_w = cam_poses[0]; // Twc0for (auto &pose : cam_poses) // 注意这里是引用pose = pose.inverse() * T_c0_w; // Tcic0 = Tciw *Twc0// Generate initial guess// 3. 使用首末位姿粗略计算出一个三维点坐标----初始解// 这里计算了一个是第一帧坐标系下的三维坐标点初始解Eigen::Vector3d initial_position(0.0, 0.0, 0.0);generateInitialGuess(cam_poses[cam_poses.size() - 1], measurements[0],measurements[measurements.size() - 1], initial_position);// 弄成逆深度形式---归一化三维点--原则上和measurements[0]的前两维度是同样的值。因为估算的时候也是在最后用measurements[0]*depth,只不过这里第三维变成了深度的倒数,即逆深度形式Eigen::Vector3d solution(initial_position(0) / initial_position(2),initial_position(1) / initial_position(2),1.0 / initial_position(2));// 列文伯格算法的相关参数double lambda = optimization_config.initial_damping;int inner_loop_cntr = 0;int outer_loop_cntr = 0;bool is_cost_reduced = false;double delta_norm = 0;// Compute the initial cost.// 4. 利用初计算的三维点(有深度)计算在各个相机下的误差,作为初始误差double total_cost = 0.0;for (int i = 0; i < cam_poses.size(); ++i){double this_cost = 0.0;// 计算投影误差(归一化坐标)cost(cam_poses[i], solution, measurements[i], this_cost);total_cost += this_cost;}// Outer loop.// 5. LM优化开始, 优化三维点坐标,不优化位姿,比较简单do{// A是 J^t * J B是 J^t * r// 可能有同学疑问自己当初学的时候是 -J^t * r// 这个无所谓,因为这里是负的更新就是正的,而这里是正的,所以更新是负的// 总之就是有一个是负的,总不能误差越来越大吧Eigen::Matrix3d A = Eigen::Matrix3d::Zero();Eigen::Vector3d b = Eigen::Vector3d::Zero();// 5.1 计算AB矩阵for (int i = 0; i < cam_poses.size(); ++i){Eigen::Matrix<double, 2, 3> J;Eigen::Vector2d r;double w;// 计算一目相机观测的雅可比与误差// J 归一化坐标误差相对于三维点的雅可比// r// w 权重,同信息矩阵jacobian(cam_poses[i], solution, measurements[i], J, r, w);// 鲁棒核约束if (w == 1){A += J.transpose() * J;b += J.transpose() * r;}else{double w_square = w * w;A += w_square * J.transpose() * J;b += w_square * J.transpose() * r;}}// Inner loop.// Solve for the delta that can reduce the total cost.// 这层是在同一个雅可比下多次迭代,如果效果不好说明需要调整阻尼因子了,因为线性化不是很好// 如果多次一直误差不下降,退出循环重新计算雅可比do{// LM算法中的lambdaEigen::Matrix3d damper = lambda * Eigen::Matrix3d::Identity();Eigen::Vector3d delta = (A + damper).ldlt().solve(b);// 更新Eigen::Vector3d new_solution = solution - delta;// 统计本次修改量的大小,如果太小表示接近目标值或者陷入局部极小值,那么就没必要继续了delta_norm = delta.norm();// 计算更新后的误差double new_cost = 0.0;for (int i = 0; i < cam_poses.size(); ++i){double this_cost = 0.0;cost(cam_poses[i], new_solution, measurements[i], this_cost);new_cost += this_cost;}// 如果更新后误差比之前小,说明确实是往好方向发展// 我们高斯牛顿的JtJ比较接近真实情况所以减少阻尼,增大步长,delta变大,加快收敛if (new_cost < total_cost){is_cost_reduced = true;solution = new_solution;total_cost = new_cost;lambda = lambda / 10 > 1e-10 ? lambda / 10 : 1e-10;}// 如果不行,那么不要这次迭代的结果// 说明高斯牛顿的JtJ不接近二阶的海森矩阵// 那么增大阻尼,减小步长,delta变小// 并且算法接近一阶的最速下降法else{is_cost_reduced = false;lambda = lambda * 10 < 1e12 ? lambda * 10 : 1e12;}} while (inner_loop_cntr++ <optimization_config.inner_loop_max_iteration &&!is_cost_reduced);inner_loop_cntr = 0;// 直到迭代次数到了或者更新量足够小了} while (outer_loop_cntr++ <optimization_config.outer_loop_max_iteration &&delta_norm > optimization_config.estimation_precision);// Covert the feature position from inverse depth// representation to its 3d coordinate.// 取出最后的结果Eigen::Vector3d final_position(solution(0) / solution(2),solution(1) / solution(2), 1.0 / solution(2));// Check if the solution is valid. Make sure the feature// is in front of every camera frame observing it.// 6. 深度验证bool is_valid_solution = true;for (const auto &pose : cam_poses){Eigen::Vector3d position =pose.linear() * final_position + pose.translation();if (position(2) <= 0){is_valid_solution = false;break;}}// 7. 更新结果// Convert the feature position to the world frame.position = T_c0_w.linear() * final_position + T_c0_w.translation();if (is_valid_solution)is_initialized = true;return is_valid_solution;
}
3.1 计算归一化坐标深度初值generateInitialGuess
这里和常规的三角化并不相同,它只是利用两个归一化坐标的一个旋转变换关系,求取某一个归一化坐标的深度。而不是真正的进行三角化,三角化路标点其中
XYZ位置,需要两个匹配点投影才可以求取。
① 理论推导

② 代码分析
这里计算了一个是第一帧坐标系下的三维坐标点初始解
归一化坐标(非像素坐标)
/*** @brief generateInitialGuess 两帧做一次三角化* @param T_c1_c2 两帧间的相对位姿* @param z1 观测1(坐标系1下归一化坐标(不是像素坐标))* @param z2 观测2 都是归一化坐标* @param p 三位点坐标*/
void Feature::generateInitialGuess(const Eigen::Isometry3d &T_c1_c2, const Eigen::Vector2d &z1,const Eigen::Vector2d &z2, Eigen::Vector3d &p) const
{// 列出方程// P2 = R21 * P1 + t21 下面省略21// 两边左乘P2的反对称矩阵// P2^ * (R * P1 + t) = 0// 其中左右可以除以P2的深度,这样P2就成了z2,且P1可以分成z1(归一化平面) 乘上我们要求的深度d// 令m = R * z1// | 0 -1 z2y | ( | m0 | )// | 1 0 -z2x | * ( | m1 | * d + t ) = 0// |-z2y z2x 0 | ( | m2 | )// 会发现这三行里面两行是线性相关的,所以只取前两行// Construct a least square problem to solve the depth.Eigen::Vector3d m = T_c1_c2.linear() * Eigen::Vector3d(z1(0), z1(1), 1.0);Eigen::Vector2d A(0.0, 0.0);A(0) = m(0) - z2(0) * m(2); // 对应第二行// 按照上面推导这里应该是负的但是不影响,因为我们下边b(1)也给取负了A(1) = m(1) - z2(1) * m(2); // 对应第一行Eigen::Vector2d b(0.0, 0.0);b(0) = z2(0) * T_c1_c2.translation()(2) - T_c1_c2.translation()(0);b(1) = z2(1) * T_c1_c2.translation()(2) - T_c1_c2.translation()(1);// Solve for the depth.// 解方程得出p1的深度值double depth = (A.transpose() * A).inverse() * A.transpose() * b;p(0) = z1(0) * depth;p(1) = z1(1) * depth;p(2) = depth; // 实际返回的是第一帧坐标系下的三维坐标点return;
}
3.2 计算归一化误差cost
函数功能:计算归一化坐标残差
计算
c0系下路标点在每一个ci系下的归一化坐标(预测),并计算归一化坐标z(观测)与预测z_hat的残差e(函数功能参考原作者代码英文注释)
① 理论推导

② 代码分析
/*** @brief cost 计算投影误差(归一化坐标)* @param T_c0_ci 相对位姿,Tcic0 每一个单相机到第一个观测的相机的T* @param x 三维点坐标(x/z, y/z, 1/z)* @param z ci帧下的观测归一化坐标* @param e 误差*/
void Feature::cost(const Eigen::Isometry3d &T_c0_ci,const Eigen::Vector3d &x, const Eigen::Vector2d &z,double &e) const
{// Compute hi1, hi2, and hi3 as Equation (37).const double &alpha = x(0);const double &beta = x(1);const double &rho = x(2);// h 等于 (R * P + t) * 1/Pz// h1 | R11 R12 R13 alpha / rho t1 |// h2 = | R21 R22 R23 * beta / rho + t2 | * rho// h3 | R31 R32 R33 1 / rho t3 |Eigen::Vector3d h =T_c0_ci.linear() * Eigen::Vector3d(alpha, beta, 1.0) + // T_c0_ci.linear()获取旋转矩阵rho * T_c0_ci.translation();double &h1 = h(0);double &h2 = h(1);double &h3 = h(2);// Predict the feature observation in ci frame.// 求出在另一个相机ci下的归一化坐标Eigen::Vector2d z_hat(h1 / h3, h2 / h3);// Compute the residual.// 两个归一化坐标算误差e = (z_hat - z).squaredNorm();return;
}
3.3 计算雅可比jacobian()
上面计算的是残差,而这里计算残差对α、β、ρ的雅可比,即对
(x/z, y/z, 1/z)的雅可比。本质是求解对三维点的雅可比,但不是直接对xyz求雅可比
① 理论推导


② 代码分析
/*** @brief jacobian 求一个观测对应的雅可比* @param T_c0_ci 相对位姿,Tcic0 每一个单相机到第一个观测的相机的T* @param x 三维点坐标(x/z, y/z, 1/z)* @param z 归一化坐标* @param J 雅可比 归一化坐标误差相对于三维点的* @param r 误差* @param w 权重* @return 是否三角化成功*/
void Feature::jacobian(const Eigen::Isometry3d &T_c0_ci,const Eigen::Vector3d &x, const Eigen::Vector2d &z,Eigen::Matrix<double, 2, 3> &J, Eigen::Vector2d &r,double &w) const
{// Compute hi1, hi2, and hi3 as Equation (37).const double &alpha = x(0); // x/zconst double &beta = x(1); // y/zconst double &rho = x(2); // 1/z// h 等于 (R * P + t) * 1/Pz// h1 | R11 R12 R13 alpha / rho t1 |// h2 = | R21 R22 R23 * beta / rho + t2 | * rho// h3 | R31 R32 R33 1 / rho t3 |Eigen::Vector3d h = T_c0_ci.linear() * Eigen::Vector3d(alpha, beta, 1.0) +rho * T_c0_ci.translation();double &h1 = h(0);double &h2 = h(1);double &h3 = h(2);// Compute the Jacobian.// 首先明确一下误差与三维点的关系// 下面的r是误差 r = z_hat - z; Eigen::Vector2d z_hat(h1 / h3, h2 / h3)// 我们要求r对三维点的雅可比,其中z是观测,与三维点坐标无关// 因此相当于求归一化坐标相对于 alpha beta rho的雅可比,首先要求出他们之间的关系// 归一化坐标设为x y// x = h1/h3 y = h2/h3// 先写出h与alpha beta rho的关系,也就是上面写的// 然后求h1 相对于alpha beta rho的导数 再求h2 的 在求 h3 的// R11 R12 t1// R21 R22 t2// R31 R32 t3// 链式求导法则// ∂x/∂alpha = ∂x/∂h1 * ∂h1/∂alpha + ∂x/∂h3 * ∂h3/∂alpha// ∂x/∂h1 = 1/h3 ∂h1/∂alpha = R11// ∂x/∂h3 = -h1/h3^2 ∂h3/∂alpha = R31// 剩下的就好求了Eigen::Matrix3d W;W.leftCols<2>() = T_c0_ci.linear().leftCols<2>();W.rightCols<1>() = T_c0_ci.translation();// h1 / h3 相对于 alpha beta rho的J.row(0) = 1 / h3 * W.row(0) - h1 / (h3 * h3) * W.row(2);// h1 / h3 相对于 alpha beta rho的J.row(1) = 1 / h3 * W.row(1) - h2 / (h3 * h3) * W.row(2);// Compute the residual.// 求取误差Eigen::Vector2d z_hat(h1 / h3, h2 / h3);r = z_hat - z;// Compute the weight based on the residual.// 使用鲁棒核函数约束double e = r.norm();if (e <= optimization_config.huber_epsilon)w = 1.0;// 如果误差大于optimization_config.huber_epsilon但是没超过他的2倍,那么会放大权重w>1// 如果误差大的离谱,超过他的2倍,缩小他的权重elsew = std::sqrt(2.0 * optimization_config.huber_epsilon / e);return;
}
3.4 计算视差checkMotion—能否三角化
checkMotion Check the input camera poses to ensure there is enough translation to triangulate the feature positon
① 理论分析
代码写的很简单,实际上就是说这角度和基线O1O2不能太小,也不能是180°,要不然达不到三角化条件。
注意:下面
feature_direction经过旋转之后还是 O 1 P O_1P O1P方向,所以简单代替,实际转换后,其为世界系下坐标,不再等同 O 1 P O_1P O1P,但方向不变!因为 R w c P c = P w − t w c R_{wc}P_c = P_w - t_{wc} RwcPc=Pw−twc,所以方向还是不变的!(或者说一个空间矢量不会因为在不同坐标系下而改变,改变的只是其在不同系下坐标)。
还有这里为什么 O 1 P O_1P O1P要乘以一个旋转,因为 O 1 O 2 O_1O_2 O1O2也是世界系下的,我们要求的点P是世界系下的,即要求这个三角形矢量也都必须在世界系。

② 代码分析
/*** @brief checkMotion 查看是否有足够视差.供外部调用* @param cam_states 所有参与计算的相机位姿* @return 是否有足够视差*/
bool Feature::checkMotion(const CamStateServer &cam_states) const
{// observations存储了所有观测到该特征的帧id和特征坐标// 1. 取出对应的始末帧idconst StateIDType &first_cam_id = observations.begin()->first;// -- 是递减运算符,用于将迭代器向前移动一个位置。--observations.end() 用于获取容器中倒数第1个元素的迭代器// observations.end()指向了容器的末尾,不是最后一个元素!const StateIDType &last_cam_id = (--observations.end())->first;// 2. 分别赋值位姿Eigen::Isometry3d first_cam_pose;// Rwc---相机状态里面记录的是qcw,所以这里转R后取了转置first_cam_pose.linear() = quaternionToRotation(cam_states.find(first_cam_id)->second.orientation).transpose();// twc---相机状态原本记录即twcfirst_cam_pose.translation() = cam_states.find(first_cam_id)->second.position;Eigen::Isometry3d last_cam_pose;// Rwclast_cam_pose.linear() = quaternionToRotation(cam_states.find(last_cam_id)->second.orientation).transpose();// twclast_cam_pose.translation() = cam_states.find(last_cam_id)->second.position;// Get the direction of the feature when it is first observed.// This direction is represented in the world frame.// 这里的意思应该是:找到第一次观测到这个特征的帧,那么把这一帧作为世界系,然后根据计算求出观测的最后一帧,// 3. 求出投影射线在世界坐标系啊下的方向// 在第一帧的左相机上的归一化坐标Eigen::Vector3d feature_direction(observations.begin()->second(0),observations.begin()->second(1), 1.0);// 归一化保证了模长是1feature_direction = feature_direction / feature_direction.norm();// 转到世界坐标系下,求出了这个射线的方向feature_direction = first_cam_pose.linear() * feature_direction;// Compute the translation between the first frame// and the last frame. We assume the first frame and// the last frame will provide the largest motion to// speed up the checking process.// 4. 求出始末两帧在世界坐标系下的位移----始指向末的向量// -----就是两帧相机光心在世界系向量O1O2 = twc2-twc1Eigen::Vector3d translation = last_cam_pose.translation() - first_cam_pose.translation(); // 这里相当于两个向量点乘 这个结果等于夹角的cos值乘上位移的模// 也相当于translation 在 feature_direction上的投影// 其实就是translation在feature_direction方向上的长度double parallel_translation = translation.transpose() * feature_direction;// 这块直接理解比较抽象,使用带入法,分别带入 0° 180° 跟90°// 当两个向量的方向相同 0°,这个值是0// 两个方向相反时 180°,这个值也是0// 90°时, cos为0,也就是看translation是否足够大,后面项是0,如果translation小于阈值,也不行// 所以这块的判断即考虑了角度,同时考虑了位移。即使90°但是位移不够也不做三角化Eigen::Vector3d orthogonal_translation = translation - parallel_translation * feature_direction;if (orthogonal_translation.norm() > optimization_config.translation_threshold)return true;elsereturn false;
}
3.5 初始化Position
/*** @brief InitializePosition Intialize the feature position* based on all current available measurements.供外部调用* @param cam_states: A map containing the camera poses with its* ID as the associated key value.* @return The computed 3d position is used to set the position* member variable. Note the resulted position is in world* frame.* @return True if the estimated 3d position of the feature* is valid.*/
inline bool initializePosition(const CamStateServer &cam_states);/*** @brief initializePosition 三角化+LM优化* @param cam_states 所有参与计算的相机位姿* @return 是否三角化成功*/
bool Feature::initializePosition(const CamStateServer &cam_states)
{// Organize camera poses and feature observations properly.// 存放每个观测以及每个对应相机的pos,注意这块是左右目独立存放std::vector<Eigen::Isometry3d, Eigen::aligned_allocator<Eigen::Isometry3d>> cam_poses(0);std::vector<Eigen::Vector2d, Eigen::aligned_allocator<Eigen::Vector2d>> measurements(0);// 1. 准备数据for (auto &m : observations){// TODO: This should be handled properly. Normally, the// required camera states should all be available in// the input cam_states buffer.auto cam_state_iter = cam_states.find(m.first);if (cam_state_iter == cam_states.end())continue;// Add the measurement.// 1.1 添加归一化坐标measurements.push_back(m.second.head<2>());measurements.push_back(m.second.tail<2>());// This camera pose will take a vector from this camera frame// to the world frame.// TwcEigen::Isometry3d cam0_pose;cam0_pose.linear() =quaternionToRotation(cam_state_iter->second.orientation).transpose();cam0_pose.translation() = cam_state_iter->second.position;Eigen::Isometry3d cam1_pose;cam1_pose = cam0_pose * CAMState::T_cam0_cam1.inverse();// 1.2 添加相机位姿cam_poses.push_back(cam0_pose);cam_poses.push_back(cam1_pose);}// All camera poses should be modified such that it takes a// vector from the first camera frame in the buffer to this// camera frame.// 2. 中心化位姿,提高计算精度Eigen::Isometry3d T_c0_w = cam_poses[0];for (auto &pose : cam_poses)pose = pose.inverse() * T_c0_w;// Generate initial guess// 3. 使用首末位姿粗略计算出一个三维点坐标Eigen::Vector3d initial_position(0.0, 0.0, 0.0);generateInitialGuess(cam_poses[cam_poses.size() - 1], measurements[0],measurements[measurements.size() - 1], initial_position);// 弄成逆深度形式Eigen::Vector3d solution(initial_position(0) / initial_position(2),initial_position(1) / initial_position(2),1.0 / initial_position(2));// Apply Levenberg-Marquart method to solve for the 3d position.double lambda = optimization_config.initial_damping;int inner_loop_cntr = 0;int outer_loop_cntr = 0;bool is_cost_reduced = false;double delta_norm = 0;// Compute the initial cost.// 4. 利用初计算的点计算在各个相机下的误差,作为初始误差double total_cost = 0.0;for (int i = 0; i < cam_poses.size(); ++i){double this_cost = 0.0;// 计算投影误差(归一化坐标)cost(cam_poses[i], solution, measurements[i], this_cost);total_cost += this_cost;}// Outer loop.// 5. LM优化开始, 优化三维点坐标,不优化位姿,比较简单do{// A是 J^t * J B是 J^t * r// 可能有同学疑问自己当初学的时候是 -J^t * r// 这个无所谓,因为这里是负的更新就是正的,而这里是正的,所以更新是负的// 总之就是有一个是负的,总不能误差越来越大吧Eigen::Matrix3d A = Eigen::Matrix3d::Zero();Eigen::Vector3d b = Eigen::Vector3d::Zero();// 5.1 计算AB矩阵for (int i = 0; i < cam_poses.size(); ++i){Eigen::Matrix<double, 2, 3> J;Eigen::Vector2d r;double w;// 计算一目相机观测的雅可比与误差// J 归一化坐标误差相对于三维点的雅可比// r// w 权重,同信息矩阵jacobian(cam_poses[i], solution, measurements[i], J, r, w);// 鲁棒核约束if (w == 1){A += J.transpose() * J;b += J.transpose() * r;}else{double w_square = w * w;A += w_square * J.transpose() * J;b += w_square * J.transpose() * r;}}// Inner loop.// Solve for the delta that can reduce the total cost.// 这层是在同一个雅可比下多次迭代,如果效果不好说明需要调整阻尼因子了,因为线性化不是很好// 如果多次一直误差不下降,退出循环重新计算雅可比do{// LM算法中的lambdaEigen::Matrix3d damper = lambda * Eigen::Matrix3d::Identity();Eigen::Vector3d delta = (A + damper).ldlt().solve(b);// 更新Eigen::Vector3d new_solution = solution - delta;// 统计本次修改量的大小,如果太小表示接近目标值或者陷入局部极小值,那么就没必要继续了delta_norm = delta.norm();// 计算更新后的误差double new_cost = 0.0;for (int i = 0; i < cam_poses.size(); ++i){double this_cost = 0.0;cost(cam_poses[i], new_solution, measurements[i], this_cost);new_cost += this_cost;}// 如果更新后误差比之前小,说明确实是往好方向发展// 我们高斯牛顿的JtJ比较接近真实情况所以减少阻尼,增大步长,delta变大,加快收敛if (new_cost < total_cost){is_cost_reduced = true;solution = new_solution;total_cost = new_cost;lambda = lambda / 10 > 1e-10 ? lambda / 10 : 1e-10;}// 如果不行,那么不要这次迭代的结果// 说明高斯牛顿的JtJ不接近二阶的海森矩阵// 那么增大阻尼,减小步长,delta变小// 并且算法接近一阶的最速下降法else{is_cost_reduced = false;lambda = lambda * 10 < 1e12 ? lambda * 10 : 1e12;}} while (inner_loop_cntr++ <optimization_config.inner_loop_max_iteration &&!is_cost_reduced);inner_loop_cntr = 0;// 直到迭代次数到了或者更新量足够小了} while (outer_loop_cntr++ <optimization_config.outer_loop_max_iteration &&delta_norm > optimization_config.estimation_precision);// Covert the feature position from inverse depth// representation to its 3d coordinate.// 取出最后的结果Eigen::Vector3d final_position(solution(0) / solution(2),solution(1) / solution(2), 1.0 / solution(2));// Check if the solution is valid. Make sure the feature// is in front of every camera frame observing it.// 6. 深度验证bool is_valid_solution = true;for (const auto &pose : cam_poses){Eigen::Vector3d position =pose.linear() * final_position + pose.translation();if (position(2) <= 0){is_valid_solution = false;break;}}// 7. 更新结果// Convert the feature position to the world frame.position = T_c0_w.linear() * final_position + T_c0_w.translation();if (is_valid_solution)is_initialized = true;return is_valid_solution;
}
4 特征管理总结
4.1 特征投影
z m , k = h ( x k ) + n k = h d ( z n , k , ζ ) + n k = h d ( h p ( C k p f ) , ζ ) + n k = h d ( h p ( h t ( G p f , G C k R , G p C k ) ) , ζ ) + n k = h d ( h p ( h t ( h r ( λ , ⋯ ) , G C k R , G p C k ) ) , ζ ) + n k \begin{aligned} \mathbf{z}_{m,k}& =\mathbf{h}(\mathbf{x}_k)+\mathbf{n}_k \\ &=\mathbf{h}_d(\mathbf{z}_{n,k}, \boldsymbol{\zeta})+\mathbf{n}_k \\ &=\mathbf{h}_d(\mathbf{h}_p(^{C_k}\mathbf{p}_f), \boldsymbol{\zeta})+\mathbf{n}_k \\ &=\mathbf{h}_d(\mathbf{h}_p(\mathbf{h}_t(^G\mathbf{p}_f, _G^{C_k}\mathbf{R}, ^G\mathbf{p}_{C_k})), \boldsymbol{\zeta})+\mathbf{n}_k \\ &=\mathbf{h}_d(\mathbf{h}_p(\mathbf{h}_t(\mathbf{h}_r(\boldsymbol{\lambda},\cdots), _G^{C_k}\mathbf{R}, ^G\mathbf{p}_{C_k})), \boldsymbol{\zeta})+\mathbf{n}_k \end{aligned} zm,k=h(xk)+nk=hd(zn,k,ζ)+nk=hd(hp(Ckpf),ζ)+nk=hd(hp(ht(Gpf,GCkR,GpCk)),ζ)+nk=hd(hp(ht(hr(λ,⋯),GCkR,GpCk)),ζ)+nk
- 特征参数转换为特征的全局坐标: G p f = h r ( λ ) ^Gp_f=h_r\left(\lambda\right) Gpf=hr(λ)
- 特征的全局坐标转到观测相机坐标系: C k p f = h t ( G p f ) {}^{C_k}p_f=h_t\left({}^Gp_f\right) Ckpf=ht(Gpf)
- 相机坐标系投影到
normalize平面: z n , k = h p ( C k p f ) z_{n,k}=h_p\left({}^{C_k}p_f\right) zn,k=hp(Ckpf) normalize平面转到图像平面: z m , k = h d ( z n , k ) z_{m,k}=h_d\left(z_{n,k}\right) zm,k=hd(zn,k)
链式法则求导:
∂ z m , k ∂ λ = ∂ z m , k ∂ z n , k ∂ z n , k ∂ C k p f ∂ C k p f ∂ G p f ∂ G p f ∂ λ \frac{\partial z_{m,k}}{\partial\lambda}=\frac{\partial z_{m,k}}{\partial z_{n,k}}\frac{\partial z_{n,k}}{\partial^{{C_{k}}}p_{f}}\frac{\partial^{{C_{k}}}p_{f}}{\partial^{G}p_{f}}\frac{\partial^{G}p_{f}}{\partial\lambda} ∂λ∂zm,k=∂zn,k∂zm,k∂Ckpf∂zn,k∂Gpf∂Ckpf∂λ∂Gpf
关于链式法则的详细推导,参考
4.2 特征参数
从上面的特征投影就能够看出,整个过程多了特征参数转换为特征全局坐标的一个步骤
对于不同的特征参数表示 λ \lambda λ,都先将其转换成世界系下的 X Y Z XYZ XYZ,即 G p f = h r ( λ ) ^Gp_f=h_r\left(\lambda\right) Gpf=hr(λ),再投影到图像上。这样做的好处在于 G p f ^{G}p_{f} Gpf到 z m , k z_{m,k} zm,k的转换关系和
Jacobian保持不变,只需要构造不同的 h r ( λ ) h_r\left(\lambda\right) hr(λ)并推导 ∂ G p f ∂ λ \frac{\partial^{G}p_{f}}{\partial\lambda} ∂λ∂Gpf,就能很快得到 ∂ z m , k ∂ λ \frac{\partial z_{m,k}}{\partial\lambda} ∂λ∂zm,k。
特征参数的表示类型由5种(openVINS文档):
① Global XYZ:$^Gp_f=h_r\left(\lambda\right)=\lambda ,推出 ,推出 ,推出\frac{\partial^{G}p_{f}}{\partial\lambda}=I$
② Global Inverse Depth(球坐标):见4.2.2
③ Anchored XYZ: λ = C a p f , G p f = h r ( λ ) = C a G R λ + G p C a \lambda={}^{C_a}p_f,{}^Gp_f=h_r\left(\lambda\right)={}_{C_a}^GR\left.\lambda+{}^Gp_{C_a}\right. λ=Capf,Gpf=hr(λ)=CaGRλ+GpCa,推出 ∂ G p f ∂ λ = C a G R \frac{\partial^{G}p_{f}}{\partial\lambda}=_{{C_{a}}}^{G}R ∂λ∂Gpf=CaGR
④ Anchored Inverse Depth(球坐标):见4.2.2
⑤ Anchored Inverse Depth (MSCKF Version):见4.2.2
注意,只有球坐标逆深度可以用在全局坐标系,因为MSCKF的逆深度当z趋于0时ρ趋于无穷,其只能用在相机坐标系,只有相机系下的特征(路标点)的深度一定大于0!在全局坐标系下,它的深度并不一定大于0。
注意
openvins将世界系中的相机位姿拆分成了IMU位姿以及相机到IMU的外参,这样是为了分别对IMU位姿和相机外参求Jacobian。
4.2.1 基于坐标系划分
Global vs Anchored:特征点的表示是全局坐标系的坐标还是局部相机坐标系的坐标。
Anchored XYZ表示选择某个相机坐标系作为Anbchor坐标系 C a {C_a} Ca。对于MSCKF里面就使用了观测到当前特征的第一帧作为anchored坐标系
4.2.2 基于XYZ或者逆深度
XYZ即直接使用空间三维点坐标进行建模,当特征较远时, Z 数值比较大,直接估计Z会存在数值问题,逆深度优势在于能够建模无穷远点。
XYZ vs Inverse Depth:使用的XYZ还是逆深度
XYZ
对于世界系
G p f = h r ( λ ) = λ ^Gp_f=h_r\left(\lambda\right)=\lambda Gpf=hr(λ)=λ
对于局部相机坐标系
λ = C a p f , G p f = h r ( λ ) = C a G R λ + G p C a \lambda={}^{C_a}p_f,{}^Gp_f=h_r\left(\lambda\right)={}_{C_a}^GR\left.\lambda+{}^Gp_{C_a}\right. λ=Capf,Gpf=hr(λ)=CaGRλ+GpCa
逆深度1:球坐标逆深度
p f = [ x f y f z f ] = 1 ρ [ cos ( θ ) sin ( ϕ ) sin ( θ ) sin ( ϕ ) cos ( ϕ ) ] λ = [ θ ϕ ρ ] = [ arctan ( y f / x f ) arccos ( z f / x f 2 + y f 2 + z f 2 ) 1 / x f 2 + y f 2 + z f 2 ] ∂ p f ∂ λ = [ − 1 ρ s i n ( θ ) sin ( ϕ ) 1 ρ c o s ( θ ) cos ( ϕ ) − 1 ρ 2 c o s ( θ ) sin ( ϕ ) 1 ρ c o s ( θ ) sin ( ϕ ) 1 ρ s i n ( θ ) cos ( ϕ ) − 1 ρ 2 s i n ( θ ) sin ( ϕ ) 0 − 1 ρ s i n ( ϕ ) − 1 ρ 2 c o s ( ϕ ) ] \begin{aligned} &p_{f}=\left[\begin{array}{c}{x_{f}}\\{y_{f}}\\{z_{f}}\end{array}\right]=\frac{1}{\rho}\left[\begin{array}{c}{\cos(\theta)\sin(\phi)}\\{\sin(\theta)\sin(\phi)}\\{\cos(\phi)}\end{array}\right] \\ &\lambda=\begin{bmatrix}\theta\\\phi\\\rho\end{bmatrix}=\begin{bmatrix}\arctan(y_f/x_f)\\\arccos\left(z_f/\sqrt{x_f^2+y_f^2+z_f^2}\right)\\1/\sqrt{x_f^2+y_f^2+z_f^2}\end{bmatrix} \\ &\left.\frac{\partial p_{f}}{\partial\lambda}=\left[\begin{array}{ccc}-\frac{1}{\rho}\mathrm{sin}(\theta)\sin(\phi)&\frac{1}{\rho}\mathrm{cos}(\theta)\cos(\phi)&-\frac{1}{\rho^{2}}\mathrm{cos}(\theta)\sin(\phi)\\\frac{1}{\rho}\mathrm{cos}(\theta)\sin(\phi)&\frac{1}{\rho}\mathrm{sin}(\theta)\cos(\phi)&-\frac{1}{\rho^{2}}\mathrm{sin}(\theta)\sin(\phi)\\0&-\frac{1}{\rho}\mathrm{sin}(\phi)&-\frac{1}{\rho^{2}}\mathrm{cos}(\phi)\end{array}\right.\right] \end{aligned} pf= xfyfzf =ρ1 cos(θ)sin(ϕ)sin(θ)sin(ϕ)cos(ϕ) λ= θϕρ = arctan(yf/xf)arccos(zf/xf2+yf2+zf2)1/xf2+yf2+zf2 ∂λ∂pf= −ρ1sin(θ)sin(ϕ)ρ1cos(θ)sin(ϕ)0ρ1cos(θ)cos(ϕ)ρ1sin(θ)cos(ϕ)−ρ1sin(ϕ)−ρ21cos(θ)sin(ϕ)−ρ21sin(θ)sin(ϕ)−ρ21cos(ϕ)
逆深度2:MSCKF逆深度
对应了
MSCKF中α、β、ρ ----(x/z, y/z, 1/z)
但MSCKF逆深度有个缺点是当z→0时,ρ→∞,存在数值奇异,所以只能用在相机坐标系,因为相机系下特征点的深度都大于0。而球坐标逆深度仅在x,y,z都趋近于0时才存在数值奇异,所以能用在全局坐标系。
p f = [ x f y f z f ] = 1 ρ [ α β 1 ] λ = [ α β ρ ] = [ x f / z f y f / z f 1 / z f ] ∂ p f ∂ λ = [ 1 ρ 0 − α ρ 2 0 1 ρ − β ρ 2 0 0 − 1 ρ 2 ] \begin{gathered}p_f=\begin{bmatrix}x_f\\y_f\\z_f\end{bmatrix}=\frac1\rho\begin{bmatrix}\alpha\\\beta\\1\end{bmatrix}\\\lambda=\begin{bmatrix}\alpha\\\beta\\\rho\end{bmatrix}=\begin{bmatrix}x_f/z_f\\y_f/z_f\\1/z_f\end{bmatrix}\\\frac{\partial p_f}{\partial\lambda}=\begin{bmatrix}\frac1\rho&0&-\frac\alpha{\rho^2}\\0&\frac1\rho&-\frac\beta{\rho^2}\\0&0&-\frac1{\rho^2}\end{bmatrix}\end{gathered} pf= xfyfzf =ρ1 αβ1 λ= αβρ = xf/zfyf/zf1/zf ∂λ∂pf= ρ1000ρ10−ρ2α−ρ2β−ρ21
如果是全局坐标系,那么上面的推到就是 ∂ G p f ∂ λ \frac{\partial^{G}p_{f}}{\partial\lambda} ∂λ∂Gpf;如果是局部相机坐标系,那么我们还需要对构建局部坐标系到世界系的变换,然后进行链式法则求导(即左乘一个旋转矩阵 C a G R ^G_{C_a}R CaGR)。
G p f = h r ( λ ) = C a G R C a p f + G p C a ∂ G p f ∂ λ = ∂ G p f ∂ C a p f ∂ C a p f ∂ λ \begin{aligned} &^Gp_f=h_r\left(\lambda\right)=_{C_a}^GR^{C_a}p_f+^Gp_{C_a} \\ &\frac{\partial^Gp_f}{\partial\lambda}=\frac{\partial^Gp_f}{\partial^{C_a}p_f}\frac{\partial^{C_a}p_f}{\partial\lambda} \end{aligned} Gpf=hr(λ)=CaGRCapf+GpCa∂λ∂Gpf=∂Capf∂Gpf∂λ∂Capf
下面求导参考openvins推导
对球坐标
对
msckf
4.3 MSCKF逆深度
MSCKF中特征参数使用了逆深度的形式,即 λ = [ α β ρ ] ⊤ \boldsymbol{\lambda}=\begin{bmatrix}\alpha&\beta&\rho\end{bmatrix}^{\top} λ=[αβρ]⊤。
使用逆深度
好处:能够表示无穷远点,当特征点较远时, z 数值比较大,直接估计 z 会存在数值问题
坏处:当z趋于0时,ρ趋于无穷大,存在数值奇异,只能用在相机坐标系中,因为相机系下坐标深度都是大于0的,不会趋于0;特别是在非相机坐标系中,因为在那里点的深度可以是负值或零。
4.4 VINS逆深度
对于VINS:仅仅使用了深度的逆作为特征参数,
λ = [ ρ ] \lambda=\begin{bmatrix}\rho\end{bmatrix} λ=[ρ]
这对应了VINS里面的优化量:姿态、外参、逆深度
[ p b i w , q b i w ] , [ p b j w , q b j w ] , [ p c b , q c b ] , λ l ∘ \begin{bmatrix}p_{b_i}^w,q_{b_i}^w\end{bmatrix}, \begin{bmatrix}p_{b_j}^w,q_{b_j}^w\end{bmatrix}, [p_c^b,q_c^b], \lambda_l\circ [pbiw,qbiw],[pbjw,qbjw],[pcb,qcb],λl∘
相关文章:

MSCKF7讲:特征管理与优化
MSCKF7讲:特征管理与优化 文章目录 MSCKF7讲:特征管理与优化1 Feature.h2 OptimizationConfig3 initializePosition三角化LM优化3.1 计算归一化坐标深度初值generateInitialGuess① 理论推导② 代码分析 3.2 计算归一化误差cost① 理论推导② 代码分析 3…...

C# XML 使用教程
C# XML 使用教程 目录 C# XML 使用教程XML 是什么介绍组成XML 与 HTML 的区别 C# 中如何使用 XML序列化根元素子元素序列化方法 反序列化反序列化方法 序列化与反序列化实例 XML 是什么 介绍 可扩展标记语言 (Extensible Markup Language, XML) ,标准通用标记语言的…...

淘宝开放平台交易类API解析以及如何测试?
调用淘宝开放平台的订单接口,主要可以通过以下几种途径进行: 1. 直接使用淘宝开放平台提供的API接口 步骤概述: 注册淘宝开放平台账号:首先,你需要在淘宝开放平台注册一个开发者账号。创建应用:在注册并…...
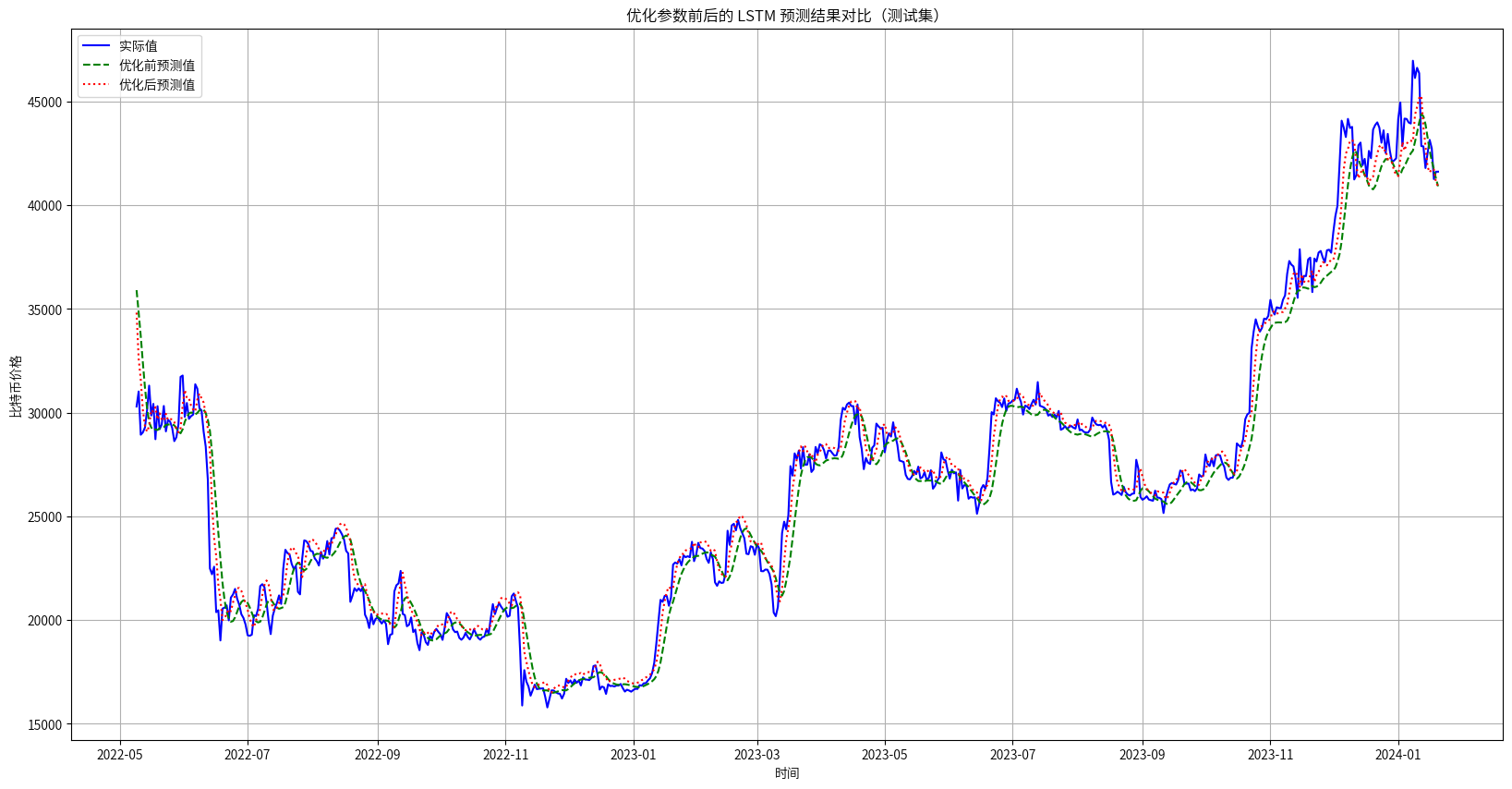
基于聚类与LSTM对比特币价格深度分析与预测
1.项目背景 比特币作为全球最具影响力的加密货币之一,其价格受到多种复杂因素的共同作用,包括市场情绪、政策变化、大型机构的投资行为等,这些因素在不同的市场阶段对比特币价格波动产生直接或间接的影响。通过对比特币市场的深入分析&#…...

YOLOv9改进策略【Neck】| 使用CARAFE轻量级通用上采样算子
一、本文介绍 本文记录的是利用CARAFE上采样对YOLOv9的颈部网络进行改进的方法研究。YOLOv9采用传统的最近邻插值的方法,仅考虑子像素邻域,无法捕获密集预测任务所需的丰富语义信息,从而影响模型在密集预测任务中的性能。CARAFE通过在大感受…...

SpringMVC上
SpringMVC介绍 MVC模型 MVC全称Model View Controller,是一种设计创建Web应用程序的模式。这三个单词分别代表Web应用程序的三个部分: Model(模型):指数据模型。用于存储数据以及处理用户请求的业务逻辑。在Web应用…...

嵌入式软件--51单片机 DAY 2
一、数码管 1.数码管概况 2.设计 (1)硬件设计 我们可以通过阴极控制显示的位置,通过阳极控制显示的内容。两个数码管共有8个阴极引脚和16个阳极引脚,如果所有引脚都直接接入MCU,会造成MCU引脚的极大浪费。 为了节省…...

高精度加法,减法,乘法,除法
加法: 大整数该如何储存? 用数组储存: 把个位放在数下标为0的位置,十位放在数组下标为1的位置(也就是高位放在数组的后面) 因为这样,如果需要增加一位最高位,那我们就可以直接在…...
)
学习计划(大三上)
第二周 总结Java并发编程的艺术 学习JVM(博客文章) 第三周 学习JVM(博客文章) 图解TCP/IP 4章 第四周 完成简历项目 学习JVM(博客文章) 图解TCP/IP 4章 第五周 完成简历项目 深入学习RocketMQ底层…...

【第0006页 · 数组】寻找重复数
【前言】本文以及之后的一些题解都会陆续整理到目录中,若想了解全部题解整理,请看这里: 第0006页 寻找重复数 今天想讨论的一道题在 LeetCode 上评论也是颇为“不错”。有一说一,是道好题,不过我们还是得先理解了它才…...

移情别恋c++ ദ്ദി˶ー̀֊ー́ ) ——10.继承
1.继承的概念及定义 1.1继承的概念 继承(inheritance)机制是面向对象程序设计使代码可以复用的最重要的手段,它允许程序员在保 持原有类特性的基础上进行扩展,增加功能,这样产生新的类,称派生类。继承呈现了面向对象 程序设计的层…...

uniapp+vue3实现双通道透明MP4播放支持小程序和h5
双通道透明MP4视频播放的截图 以下是合成后结果,二个合并在一起进行播放 下载资源,打开运行直接使用看到效果 https://download.csdn.net/download/qq_40039641/89715780...

汇编:嵌入式软件架构学习资源
成为嵌入式软件架构设计师需要掌握多方面的知识,包括嵌入式系统、实时操作系统、硬件接口、软件设计模式等。 以下是一些推荐的博客和网站,可以帮助你深入学习嵌入式软件架构设计: ### 1. **Embedded.com** - **网址**: [Embedded.com](htt…...

python编程知识(实现数据加密和解密)
👨💻个人主页:开发者-曼亿点 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 曼亿点 原创 👨💻 收录于专栏:…...
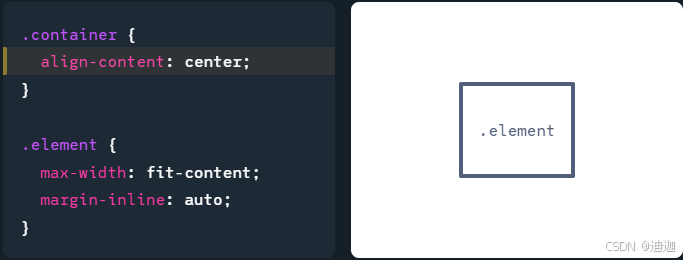
如何使div居中?CSS居中终极指南
前言 长期以来,如何在父元素中居中对齐一个元素,一直是一个让人头疼的问题,随着 CSS 的发展,越来越多的工具可以用来解决这个难题,五花八门的招式一大堆,这篇博客,旨在帮助你理解不同的居中方法…...

Redis 篇-深入了解分布式锁 Redisson 原理(可重入原理、可重试原理、主从一致性原理、解决超时锁失效)
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 本章目录 1.0 基于 Redis 实现的分布式锁存在的问题 2.0 Redisson 功能概述 3.0 Redisson 具体使用 4.0 Redisson 可重入锁原理 5.0 Redisson 锁重试原理 6.0 Redisson WatchDo…...
深入解析)
PostgreSQL中的多版本并发控制(MVCC)深入解析
引言 PostgreSQL作为一款强大的开源关系数据库管理系统,以其高性能、高可靠性和丰富的功能特性而广受欢迎。在并发控制方面,PostgreSQL采用了多版本并发控制(MVCC)机制,该机制为数据库提供了高效的数据访问和更新能力…...

SpringBoot项目-实现简单的CRUD功能和分页查询
背景 本博文主要是创建了一个新的SpringBoot项目,实现基本的增删改查,分页查询,带条件的分页查询功能。是方便初学者学习后端项目的一个比较清晰明了的实践代码,读者可根据博文,从自己动手创建一个新的SpringBoot项目…...

CCF编程能力等级认证GESP—C++2级—20240907
CCF编程能力等级认证GESP—C2级—20240907 单选题(每题 2 分,共 30 分)判断题(每题 2 分,共 20 分)编程题 (每题 25 分,共 50 分)数位之和小杨的矩阵 单选题(每题 2 分,共…...

C语言手撕实战代码_二叉排序树(二叉搜索树)_构建_删除_插入操作详解
二叉排序树习题1.设计算法构建一棵二叉排序树(又称二叉搜索树BST)2.查找二叉排序树中结点为x的结点所在的层数3.删除二叉排序树T中值为x的结点4.查找二叉排序树中所有小于key的关键字5.编写算法,将一棵二叉树t分解成两棵二叉排序树t1和t2,使得t1中的所有…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...

6.9-QT模拟计算器
源码: 头文件: widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMouseEvent>QT_BEGIN_NAMESPACE namespace Ui { class Widget; } QT_END_NAMESPACEclass Widget : public QWidget {Q_OBJECTpublic:Widget(QWidget *parent nullptr);…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...
