数学-快速幂
从一个简单的问题说起:
给出整数m,n和p,要求计算(m ^ n) % p的结果。
#include <iostream>
using namespace std;int main() {long long m, n, p;cin >> m >> n >> p;long long ans = 1;for (long long i = 0; i < n; i++) {ans = ans * m;}cout << ans << "\n";return 0;
}这个程序似乎正确了,但是存在严重问题:
<1>.m或n太大,极容易溢出.
<2>.如果n的值太大,时间消耗O(n)代价较大.
首先解决溢出的问题:
显然:
(a * b) % c = ((a % c) * (b % c)) % c.
这样,就可以把程序改写为如下形式:
但是,如果n的值太大,时间消耗O(n)代价太大,这个问题如何解决呢?
#include <iostream>
using namespace std;int main() {long long m, n, p;cin >> m >> n >> p;long long ans = 1;for (long long i = 0; i < n; i++) {ans = ((ans % p) * (m % p)) % p;}cout << ans << "\n";return 0;
}乘方快速幂:
假设要计算 m^10,m^10 = (m^5) ^ 2 = (m * (m ^ 2) ^ 2) ^ 2.
也就是说,要计算m ^ n,有:

那么,程序就变成了:
#include <iostream>
using namespace std;int main() {long long m, n, p;cin >> m >> n >> p;long long ans = 1;while (n) {if (n % 2 != 0) {ans = ((ans % p) * (m % p)) % p;}n = n / 2;m = ((m % p) * (m % p)) % p;}cout << ans << "\n";return 0;
}但是,对于这个程序,我们仍可以继续对其优化:
首先介绍一下 按位与运算(&) 与 右移运算(>>):
<1>.按位与运算:
对于两个二进制数,它们按位与运算的结果是: 对于每一位,如果两个数的这一位同时为1,那么按位与的结果便是1,否则为0,最后将结果转化为十进制,就是我们想要的答案了。 对于一个整数,如果它是奇数,那么它的二进制表示的最低位为1,否则为0,那么对于奇数而言,其按位与1的结果是1,对于偶数而言,其按位与1的结果是0,由此我们可以通过判断一个整数按位与1的结果来判断其是偶数还是奇数.
<2>.右移运算:
同样是对2进制数进行处理,将所有位置上的数字右移,高位补0:如5:101,右移一位为010,结果是2。则:对于一个整数而言,右移一位,相当于其除以2并向下取整。
我们可以根据这两个运算来初步优化程序:
即将 n % 2 != 0 改为 n & 1 == 1,将 n = n / 2 改为 n = n >> 1.
#include <iostream>
using namespace std;int main() {long long m, n, p;cin >> m >> n >> p;long long ans = 1;while (n) {if (n & 1) {ans = ((ans % p) * (m % p)) % p;}n = n >> 1;m = ((m % p) * (m % p)) % p;}cout << ans << "\n";return 0;
}对于m ^ 0,结果为1,1 % 1 == 0,所以,我们应该要防止这种特殊情况,即在进行乘方运算之前,先将ans % p:
#include <iostream>
using namespace std;int main() {long long m, n, p;cin >> m >> n >> p;long long ans = 1 % p;while (n) {if (n & 1) {ans = ((ans % p) * (m % p)) % p;}n = n >> 1;m = ((m % p) * (m % p)) % p;}cout << ans << "\n";return 0;
}因为C++内置的最高整数类型是64位,若运算 (a ^ b) % p中的三个变量a,b,p都在10^18级别,则不存在一个可供强制转化的128位整数类型,我们需要一些特殊的处理办法:
进行乘方运算之前,先让m对p取模一次:
#include <iostream>
using namespace std;int main() {long long m, n, p;cin >> m >> n >> p;long long ans = 1 % p;m %= p;while (n) {if (n & 1) {ans = ((ans % p) * (m % p)) % p;}n = n >> 1;m = ((m % p) * (m % p)) % p;}cout << ans << "\n";return 0;
}这样就是最优的形式了。
下面给出几道相关的练习题:
Raising Modulo Numbers
我们可以计算每一项a^b的值,然后将其加起来作为结果:
#include <iostream>
#define i64 long longi64 qpow(i64 a, i64 b, i64 p) {i64 ans = 1 % p;a %= p;while (b) {if (b & 1) {ans = ((ans % p) * (a % p)) % p;}b >>= 1;a = ((a % p) * (a % p)) % p;}return ans;
}int main() {int t; std::cin >> t;while (t--) {i64 M;std::cin >> M;i64 H, ans = 0;std::cin >> H;for (int i = 0; i < H; i++) {i64 A, B;std::cin >> A >> B;ans = ((ans % M) + (qpow(A, B, M) % M)) % M;}std::cout << ans << "\n";}return 0;
}Pseudoprime numbers
题意:
输入p 和 a,如果p不是质数,并且a>1并且(a^p) % p == a % p,那么输出yes,否则输出no
参考代码:
#include <iostream>
using namespace std;bool isprime(long long n) {if (n < 2) {return false;}for (int i = 2; i <= n / i; i++) {if (n % i == 0) {return false;}}return true;
}long long qpow(long long m, long long n, long long p) {long long ans = 1 % p;while (n) {if (n & 1) {ans = ((ans % p) * (m % p)) % p;}n = n >> 1;m = ((m % p) * (m % p)) % p;}return ans;
}int main() {long long p, a;while (cin >> p >> a && p && a) {if (isprime(p) == false && qpow(a, p, p) == a % p && a > 1) {cout << "yes\n";} else {cout << "no\n";}}return 0;
}方阵快速幂:

相关文章:

数学-快速幂
从一个简单的问题说起: 给出整数m,n和p,要求计算(m ^ n) % p的结果。 #include <iostream> using namespace std;int main() {long long m, n, p;cin >> m >> n >> p;long long ans 1;for (long long i 0; i < …...

DevEco鸿蒙应用开发-第一个App
目录下载开发环境创建工程登录华为账户测试应用下载开发环境 前往官网下载 DevEco 开发环境:https://developer.harmonyos.com/cn/develop/deveco-studio#download 下载并安装,请记住你选择的 IDE 与 SDK 安装位置,后续可能会用到ÿ…...
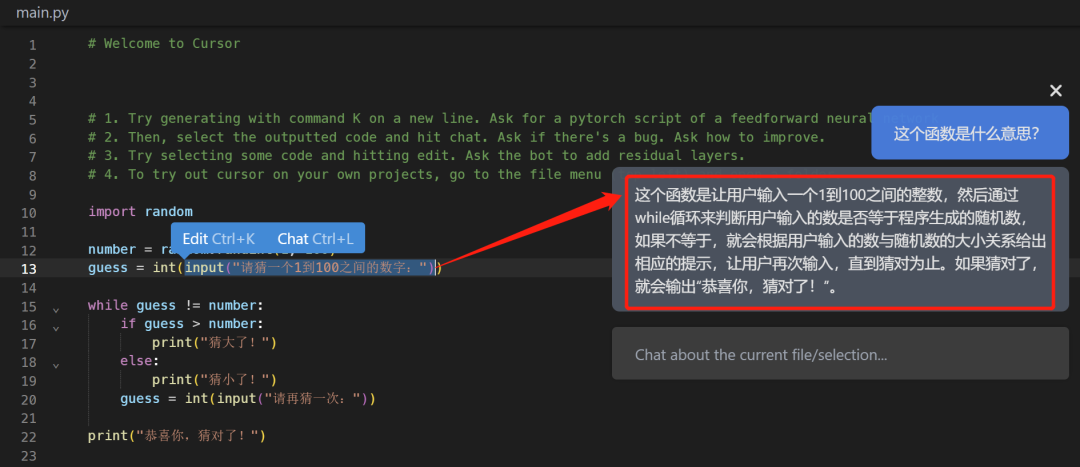
又一款全新的基于 GPT4 的 Python 神器Cursor,关键还免费
chartgpt大火之后,随之而来的就是一大类衍生物了。 然后,今天要给大家介绍的是一款基于GPT4的新一代辅助编程神器——Cursor。 它最值得介绍的地方在于它免费,我们可以直接利用它来辅助我们编程,真正做到事半功倍。 注意&#…...

CSS的浮动(下)
🌟所属专栏:前端只因变凤凰之路🐔作者简介:rchjr——五带信管菜只因一枚😮前言:该系列将持续更新前端的相关学习笔记,欢迎和我一样的小白订阅,一起学习共同进步~👉文章简…...

软件测试-性能测试流程
压测任务具体包含: 0.前期准备 尽量参与业务需求评审,可以对业务有更深入的了解,了解哪些功能是核心功能,哪些可能存在性能瓶颈,以便在性能需求评审的时候能给出有建设性的意见 1.性能需求分析、评审 明确测试范围(哪些业务接口)、目标(tps、rt、成功率) 关于性能需…...

【python实操】年轻人,别用记事本保存数据了,试试数据库吧
为什么用数据库? 数据库比记事本强在哪? 答案很明显,你的文件很多时候都只能被一个人打开,不能被重复打开。当有几百万数据的时候,你如何去查询操作数据,速度上要快,看起来要清晰直接 数据库比我…...
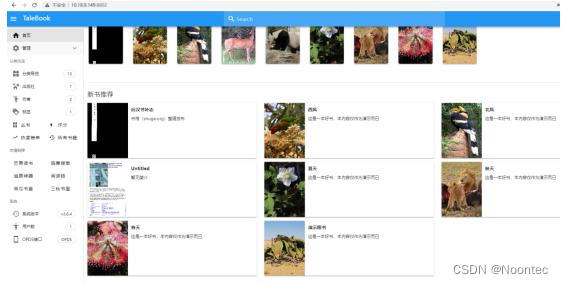
铁威马NAS教程之利用docker快速搭建个人在线书库
这是一个基于Calibre的简单的图书管理系统,支持在线阅读。主要特点是:美观的界面、支持多用户、支持在线阅读、支持邮件推送、支持OPDS、支持一键安装,网页版初始化配置,轻松启动网站等等。 那么,如何利用docker快速搭…...

504. 七进制数——【Leetcode每日一题】
504. 七进制数 给定一个整数 num,将其转化为 7 进制,并以字符串形式输出。 示例 1: 输入: num 100 输出: “202” 示例 2: 输入: num -7 输出: “-10” 提示: −107<num<107-10^7 < num < 10^7−107<num<107 思路&…...
—DefaultMQPushConsumer延迟消息源码)
RocketMQ源码(24)—DefaultMQPushConsumer延迟消息源码
基于RocketMQ release-4.9.3,深入的介绍了DefaultMQPushConsumer延迟消息源码。 文章目录1 load加载延迟消息数据1.1 parseDelayLevel解析延迟等级2 start启动调度消息服务3 DeliverDelayedMessageTimerTask投递延迟消息任务3.1 executeOnTimeup执行延迟消息投递3.2…...
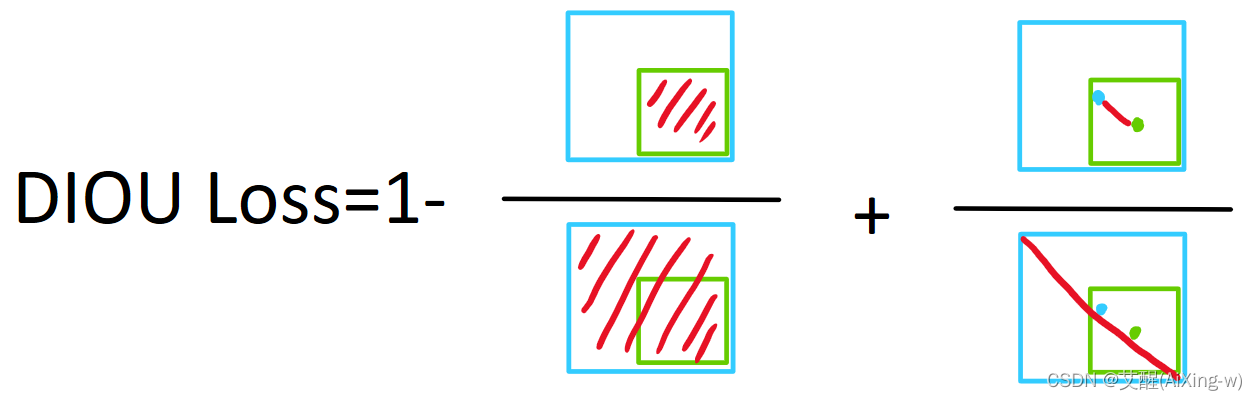
计算机视觉知识点(一)——交并比(IoU)及其若干改进
交并比(IoU)前言IoU公式及示意图IoU Loss缺点GIoU Loss公式及示意图缺点DIoU公式及示意图CIoU前言 目标检测是一个常见的计算机视觉任务,在目标检测任务中,交并比作为评判检测框的标准具有很重要的意义,在实际的应用中…...

一篇文章教你从零到一搭建自动化测试框架(附视频教程+源码)
目录 前言 1. 什么是自动化测试框架? 2. 没有万能的测试框架,适合自己项目的,能提高工作效率的就是好框架。 3. 设计框架的思路: 4.如何开展自动化测试 前言 关于测试框架的好处,比如快速回归提高测试效率&#x…...

【备战蓝桥杯】----01背包问题(动态规划)
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...

Golang1.18新特性介绍——泛型
社区长期高呼的泛型特性在Golang 1.18中终于正式发布,Go泛型实现与传统的C有较大差异,更像Rust的泛型实现。本文详细介绍Golang泛型及其特性,包括泛型语法、类型参数、类型约束、类型近似以及constraints包提供内置类型等。 最近写Dao代码&am…...
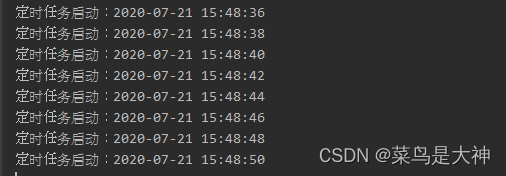
【SpringBoot17】SpringBoot中使用Quartz管理定时任务
定时任务在系统中用到的地方很多,例如每晚凌晨的数据备份,每小时获取第三方平台的 Token 信息等等,之前我们都是在项目中规定这个定时任务什么时候启动,到时间了便会自己启动,那么我们想要停止这个定时任务的时候&…...

杨辉三角形 (蓝桥杯) JAVA
目录题目描述:暴力破解(四成):二分法破解(满分):题目描述: 下面的图形是著名的杨辉三角形: 如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如…...

AI制药 - AlphaFold Multimer 的 MSA Pairing 源码
目前最新版本是v2.3.1,2023.1.12 AlphaFold multimer v1 于 2021 年 7 月发布,同时发表了一篇描述其方法和结果的论文。AlphaFold multimer v1 使用了与 AlphaFold 单体相同的模型结构和训练方法,但增加了一些特征和损失函数来处理多条链。Al…...

TitanIDE:云原生开发到底强在哪里?
原文作者:行云创新技术总监 邓冰寒 引言 是一种新的软件开发方法,旨在构建更可靠、高效、弹性、安全和可扩展的应用程序。与传统的应用程序开发方式不同,云原生是将开发环境完全搬到云端,构建一站式的云原生开发环境。云原生的开…...

单片机常用完整性校验算法
一、前言 单片机在开发过程中经常会遇到大文件传输,或者大量数据传输,在一些工业环境下,数据传输并不是很稳定,如何检验数据的完整性就是个问题,这里简单介绍一下单片机常用的几种数据完整性校验方法。 二、CheckSum校…...
Anaconda 的安装配置及依赖项的内外网配置
在分享anaconda 的安装配置及使用前,我们必须先明白anaconda是什么;Anaconda是一个开源的Python发行版本。两者区别在于前者是一门编程语言,后者相当于编程语言中的工具包。 由于python自身缺少numpy、matplotlib、scipy、scikit-learn等一系…...
p84 CTF夺旗-PHP弱类型异或取反序列化RCE
数据来源 文章参考 本课重点: 案例1:PHP-相关总结知识点-后期复现案例2:PHP-弱类型对比绕过测试-常考点案例3:PHP-正则preg_match绕过-常考点案例4:PHP-命令执行RCE变异绕过-常考点案例5:PHP-反序列化考题…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...
