杨辉三角形 (蓝桥杯) JAVA
目录
- 题目描述:
- 暴力破解(四成):
- 二分法破解(满分):
题目描述:
下面的图形是著名的杨辉三角形:
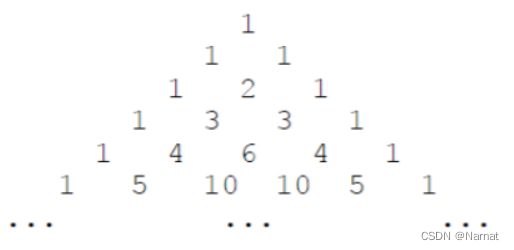
如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如下数列:
1, 1, 1, 1, 2, 1, 1, 3, 3, 1, 1, 4, 6, 4, 1, ...给定一个正整数 N,请你输出数列中第一次出现 N 是在第几个数?
输入格式:
输入一个整数 N。
输出格式:
输出一个整数代表答案。
数据范围:
对于 20% 的评测用例,
1≤N≤10;
对于所有评测用例,1≤N≤10^9。
输入样例:
6
输出样例:
13
暴力破解(四成):
解题思路:
解决本难题的话,如果不是很了解杨辉三角的规律的话,可以用暴力混分。
想要暴力混分,得先明白杨辉三角形的最基本规的律:
1
1 1
1 2 1
1 3 3 1
1 2 6 4 1
1.每行首尾都是1
2.每行数字左右对称
3.第n行的数字有n列
4.每列上的元素值 = 上一行当前列元素值 + 上一行上一列元素值
了解上述基本规律就能将杨辉三角存入二维数组中,再输出。
对于本题我采用的是一维滚动数组来更新杨辉三角的值,因为一维数组最大可以分配 大概1 * 10^9左右的空间,能打印杨辉三角的最大宽度就很大了。而二维数组分配 10000*10000的空间就爆炸了。能打印杨辉三角的最大宽度就缩短了。
值得注意的是,更新一维数组的时候要从后往前更新,由于杨辉三角是具有对称性,所以不影响(从前往后更新的话,数据会被覆盖)。
用一维数组打印杨辉三角的代码如下:
import java.util.*;public class Main{public static long n = 0;public static void main(String[] args){long a[] = new long[1000000 + 1];for(int i = 0; i <= 10; i ++) {for(int j = i; j >= 0; j --) {if(j == 0 || i == j) {a[j] = 1L;System.out.print(a[j] + " ");continue;}a[j] = a[j] + a[j - 1];System.out.print(a[j] + " ");}System.out.println();} }
}
用暴力破解本题,代码如下:
import java.util.*;public class Main{public static long n = 0;public static void main(String[] args){Scanner sc = new Scanner(System.in);n = sc.nextLong();long a[] = new long[1000000 + 1];long sum = 0;out : for(int i = 0; i <= 1000000; i ++) {for(int j = i; j >= 0; j --) {if(j == 0 || i == j) a[j] = 1L;else a[j] = a[j] + a[j - 1];if(a[j] == n) {sum ++;System.out.println(sum);break out;}sum ++;}}}
}
上代码在官方平台能拿四成分数,虽然不多,但如果只会暴力的话这么些代码,得这些分也是可以接受的:

二分法破解(满分):
思路:
要使用二分法破解本题,就要对杨辉三角形,每个位置上的元素规律都有进一步的了解。
下面直接给出结论:

上图可知,左边与右边对称,所以只需要研究左边即可。
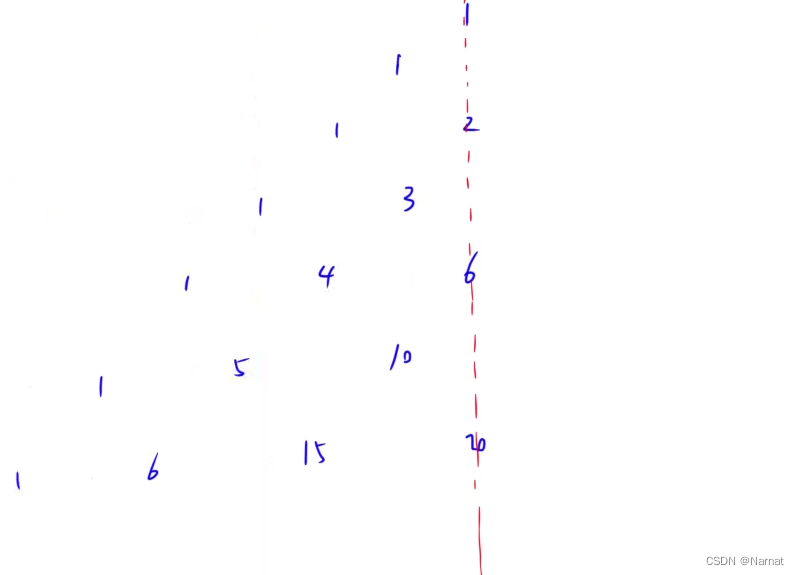
上述的一半可以直接用下方的排列组合式子表示:

加一些标注如下图:
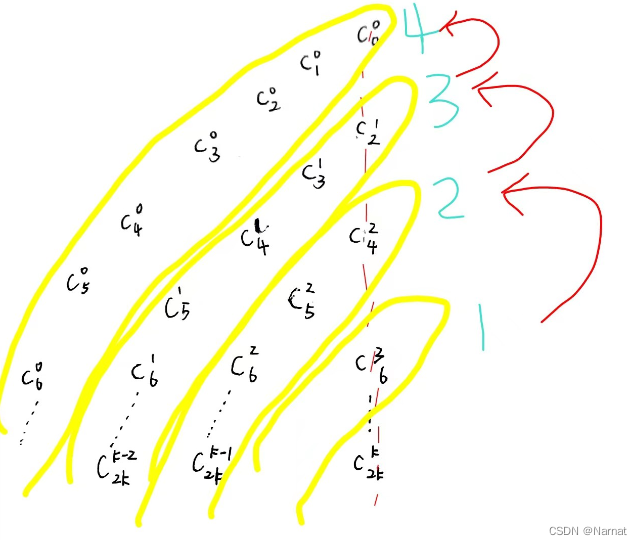
注意要求找到n第一次出现的位置:
很容易可以看到每一层 斜排 内的元素从上往下都是单调递增的,且越靠内扩张越快。所以靠内斜排 上的元素扩张的最快,所以能最快碰到第一个n。所以在二分查找的时候我们从内层往 外层 找(这样找到的 n 就是第一次出现的),由于杨辉三角扩散速度很快,所以 16 斜层 就可以包含10^9的数据。
如上图标记,我们从内往外,先 找 1 层,看是否有一个 C(r , k) = n 如果有的话我们直接退出,否者继续去找 2 层…直到找到一个C(r, k) = n 再通过r, k 找到这个数是第几次出现的(用N表示)。
这里直接给出结论:N = r *(r + 1) + k + 1
(上述公式只要知道:r, k 是从 0 开示的就不难推出N)
还需要注意的是本题用long变量储存数据,出现 long >> 1 + int 类型的式子是很容易让最终结果出错的。
例如:
public class text {public static void main(String[] args) {long a = 2L;System.out.print(a >> 1 + 1);}
}
输出:
修改方法有两种,正确代码:
public class text {public static void main(String[] args) {long a = 2L;long b = 1L;System.out.println((long)(a >> 1) + 1L);System.out.print(a / 2 + 1);}
}
输出:

理论成立本题完整代码如下:
import java.util.*;public class Main{public static int n = 0;public static void main(String[] args){Scanner sc = new Scanner(System.in);n = sc.nextInt();//别写成int nfor(int i = 16; i >= 0; i --) if(check(i)) break;
} public static long C(long a, long b) {//求排列组合C(a,b)的值long res = 1;//不要写成res = 0;for(long i = a, j = 1; j <= b; j ++, i --) {res = res * i / j;if(res > n) return res;//大于n直接退出防止爆long}return res;}public static boolean check(int k) {long L = 2 * k;//C(2*k, k) ~ C(N, k),这个区间内寻找一个C(r, k) = nlong R = n;//左右边界,C(1, n) = n,所以右边界最多是n while(L <= R) {long middle = (L + R) >> 1;//高效 除 2long nt = C(middle, k);if(nt > n) R = middle - 1;//大于查左边部分else if(nt < n) L = middle + 1;else {System.out.print((middle *(middle + 1)) / 2 + k + 1);//输出结果,再退出return true;} }return false;}
}

相关文章:

杨辉三角形 (蓝桥杯) JAVA
目录题目描述:暴力破解(四成):二分法破解(满分):题目描述: 下面的图形是著名的杨辉三角形: 如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如…...

AI制药 - AlphaFold Multimer 的 MSA Pairing 源码
目前最新版本是v2.3.1,2023.1.12 AlphaFold multimer v1 于 2021 年 7 月发布,同时发表了一篇描述其方法和结果的论文。AlphaFold multimer v1 使用了与 AlphaFold 单体相同的模型结构和训练方法,但增加了一些特征和损失函数来处理多条链。Al…...

TitanIDE:云原生开发到底强在哪里?
原文作者:行云创新技术总监 邓冰寒 引言 是一种新的软件开发方法,旨在构建更可靠、高效、弹性、安全和可扩展的应用程序。与传统的应用程序开发方式不同,云原生是将开发环境完全搬到云端,构建一站式的云原生开发环境。云原生的开…...

单片机常用完整性校验算法
一、前言 单片机在开发过程中经常会遇到大文件传输,或者大量数据传输,在一些工业环境下,数据传输并不是很稳定,如何检验数据的完整性就是个问题,这里简单介绍一下单片机常用的几种数据完整性校验方法。 二、CheckSum校…...
Anaconda 的安装配置及依赖项的内外网配置
在分享anaconda 的安装配置及使用前,我们必须先明白anaconda是什么;Anaconda是一个开源的Python发行版本。两者区别在于前者是一门编程语言,后者相当于编程语言中的工具包。 由于python自身缺少numpy、matplotlib、scipy、scikit-learn等一系…...
p84 CTF夺旗-PHP弱类型异或取反序列化RCE
数据来源 文章参考 本课重点: 案例1:PHP-相关总结知识点-后期复现案例2:PHP-弱类型对比绕过测试-常考点案例3:PHP-正则preg_match绕过-常考点案例4:PHP-命令执行RCE变异绕过-常考点案例5:PHP-反序列化考题…...

2022财报逆转,有赞穿透迷雾实现突破
2022年,商家经营面临困难。但在一些第三方服务商的帮助下,也有商家取得了逆势增长。 2023年3月23日,有赞发布2022年业绩报告,它帮助许多商家稳住了一整年的经营。2022年,有赞门店SaaS业务的GMV达到425亿元,…...

蓝桥杯 - 求组合数【C(a,b)】+ 卡特兰数
文章目录💬前言885. 求组合数 I C(m,n) 【dp】886 求组合数 II 【数据大小10万级别】 【费马小定理快速幂逆元】887. 求组合数 III 【le18级别】 【卢卡斯定理 逆元 快速幂 】888.求组合数 IV 【没有%p -- 高精度算出准确结果】 【分解质因数 高精度乘法 --只用一…...

膳食真菌在癌症免疫治疗中的作用: 从肠道微生物群的角度
谷禾健康 癌症是一种恶性肿瘤,它可以发生在人体的任何部位,包括肺、乳房、结肠、胃、肝、宫颈等。根据世界卫生组织的数据,全球每年有超过1800万人被诊断出患有癌症,其中约有1000万人死于癌症。癌症已成为全球范围内的主要健康问题…...

怎么将模糊的照片变清晰
怎么将模糊的照片变清晰?珍贵的照片每个人都会有,而遇到珍贵的照片变模糊了,相信会让人很苦恼的。那么有没有办法可以解决呢?答案是有的,我们可以用工具让模糊的照片变得清晰。下面就来分享一些让模糊的照片变清晰的方法,有兴趣…...
【软件测试】基础知识第一篇
文章目录一. 什么是软件测试二. 测试和调试的区别三. 什么是测试用例四. 软件的生命周期五. 软件测试的生命周期一. 什么是软件测试 软件测试就是验证软件产品特性是否满足用户的需求。 那需求又是什么呢?在多数软件公司,会有两种需求,一种…...

【百面成神】java web基础7问,你能坚持到第几问
前 言 🍉 作者简介:半旧518,长跑型选手,立志坚持写10年博客,专注于java后端 ☕专栏简介:纯手打总结面试题,自用备用 🌰 文章简介:java web最基础、重要的8道面试题 文章目…...

Centos7安装、各种环境配置和常见bug解决方案,保姆级教程(更新中)
文章目录前言一、Centos7安装二、各种环境配置与安装2.1 安装net-tools(建议)2.2 配置静态网络(建议)2.1 修改Centos7的时间(建议)2.2 Centos7系统编码问题2.3 vim安装(建议)2.4 解决…...

【C++进阶】智能指针
文章目录为什么需要智能指针?内存泄漏什么是内存泄漏,内存泄漏的危害内存泄漏分类(了解)如何避免内存泄漏智能指针的使用及原理smart_ptrauto_ptrunique_ptrshared_ptr线程安全的解决循环引用weak_ptr删除器为什么需要智能指针&am…...

软件测试面试题 —— 整理与解析(3)
😏作者简介:博主是一位测试管理者,同时也是一名对外企业兼职讲师。 📡主页地址:🌎【Austin_zhai】🌏 🙆目的与景愿:旨在于能帮助更多的测试行业人员提升软硬技能…...

springboot常用的20个注解
Spring Boot方式的项目开发已经逐步成为Java应用开发领域的主流框架,它不仅可以方便地创建生产级的Spring应用程序,还能轻松地通过一些注解配置与目前比较火热的微服务框架SpringCloud集成, 而Spring Boot 之所以能够轻松地实现应的创建及与…...

USB组合设备——带鼠标功能的键盘
文章目录带鼠标功能的键盘一个接口实现报告描述符示例多个接口实现复合设备和组合设备配置描述符集合的实现报告的返回附 STM32 枚举日志复合设备:Compound Device 内嵌 Hub 和多个 Function,每个 Function 都相当于一个独立的 USB 外设,有自…...
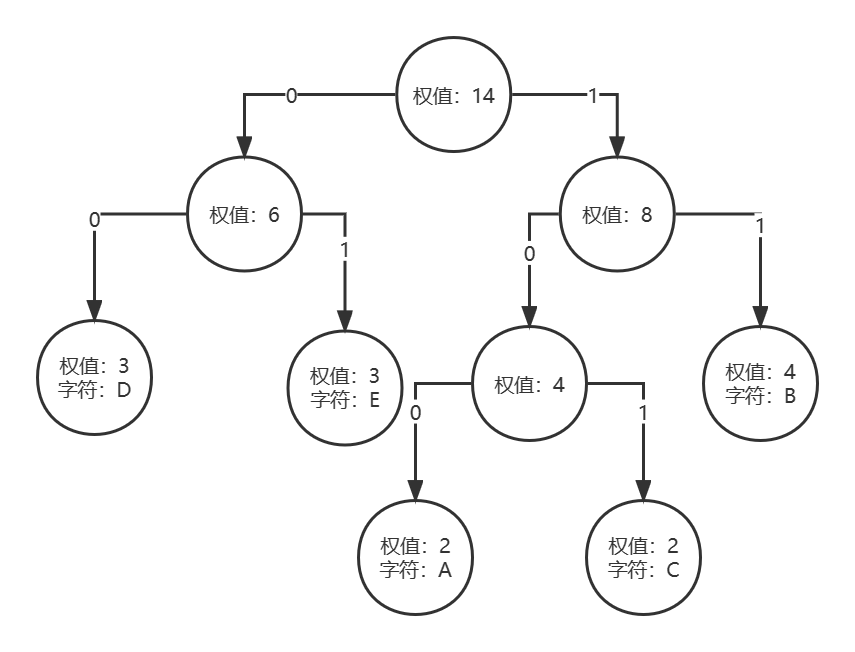
数据结构与算法基础-学习-18-哈夫曼编码
一、个人理解在远程通讯中,需要把字符转成二进制的字符串进行传输,例如我们需要传输ABCD,我们可以用定长的字符串进行表示,例如:A:00B:01C:02D:03这样可能就造成空间的浪费,我们多存储了一个0号位。那用变长呢…...

ZMC408CE | 实现“8通道独立PSO”应用场景
一、ZMC408SCAN产品亮点 1.高性能处理器,提升运算速度、响应时间和扫描周期等; 2.一维/二维/三维、多通道视觉飞拍,高速高精; 3.位置同步输出PSO,连续轨迹加工中对精密点胶胶量控制和激光能量控制等; 4…...

QuickJS中JS_SetClassProto方法把JavaScript对象指定为某个类的原型对象
在 QuickJS 中,JS_SetClassProto 方法用于设置一个类的原型对象。这个方法的作用是将一个 JavaScript 对象指定为该类的原型对象,从而定义该类的属性和方法。 具体来说,JS_SetClassProto 方法的第一个参数是指向 QuickJS 引擎执行上下文的指…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...
