铁威马NAS教程之利用docker快速搭建个人在线书库
这是一个基于Calibre的简单的图书管理系统,支持在线阅读。主要特点是:美观的界面、支持多用户、支持在线阅读、支持邮件推送、支持OPDS、支持一键安装,网页版初始化配置,轻松启动网站等等。
那么,如何利用docker快速搭建个人在线书库,以铁威马F4-423为例。
1.首先创建好TaleBook文件夹。

2.登录铁威马TOS系统后,前往TOS 应用中心,找到Docker应用,然后点击“安装”。
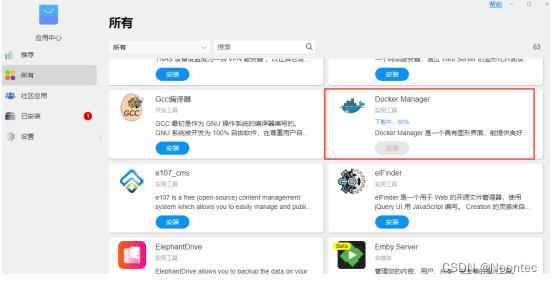
3.单击桌面打开Docker,注册表,在搜索框中输入talebook,点击下载。

4.下载完成后,选中下载好的镜像,点击启动。

5.设置容器名称,设置资源限制,是否开机自动启动,点击下一步。

6.设置卷,路径选择刚刚创建的文件夹,点击下一步。

7.设置端口,点击下一步(本地端口可以自定义,只要不和其他端口冲突就行,如需外网访问,需将这个端口在路由器上做好转发)。

8.一直下一步,确认完成。
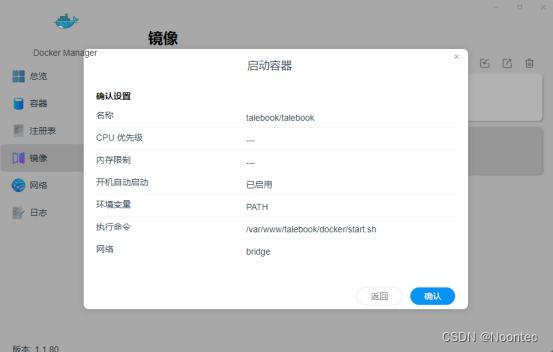
9.可以在容器界面查看。

10.设置完docker镜像后,就可以通过网页来访问媒体服务器了,访问地址是铁威马IP+docker容器的本地端口。
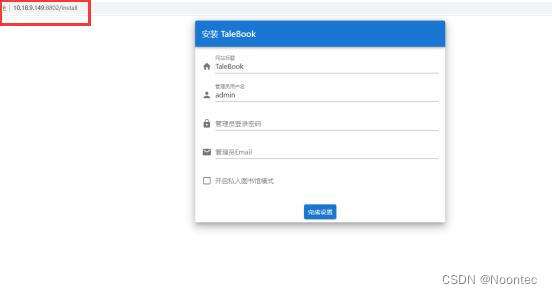
11.设置网站标题、用户名、密码、邮箱,,完成填写后,点击完成设置。
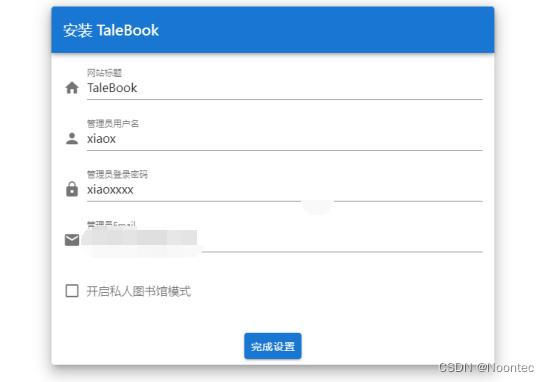
12.右上角登录。

13.进入首页。

14.将你的书箱上传到此前NAS中建立的文件夹Docker/Talebook,找到books/imports目录,上传成功后,在网页左上角找到管理,并进入导入图书页面,点击扫描书籍。
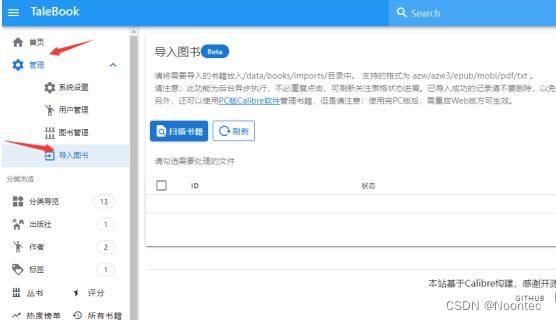
15.勾选需要上传的书籍,导入书架。

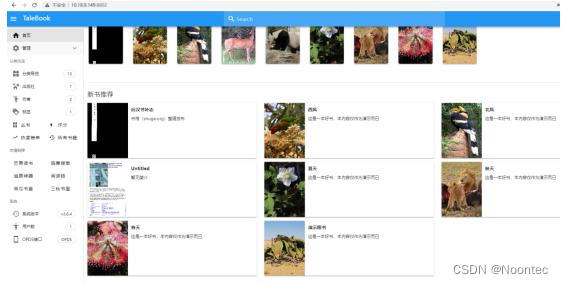
16.回到首页就可以看到了,你可以点击文档上线阅读。
相关文章:

铁威马NAS教程之利用docker快速搭建个人在线书库
这是一个基于Calibre的简单的图书管理系统,支持在线阅读。主要特点是:美观的界面、支持多用户、支持在线阅读、支持邮件推送、支持OPDS、支持一键安装,网页版初始化配置,轻松启动网站等等。 那么,如何利用docker快速搭…...

504. 七进制数——【Leetcode每日一题】
504. 七进制数 给定一个整数 num,将其转化为 7 进制,并以字符串形式输出。 示例 1: 输入: num 100 输出: “202” 示例 2: 输入: num -7 输出: “-10” 提示: −107<num<107-10^7 < num < 10^7−107<num<107 思路&…...
—DefaultMQPushConsumer延迟消息源码)
RocketMQ源码(24)—DefaultMQPushConsumer延迟消息源码
基于RocketMQ release-4.9.3,深入的介绍了DefaultMQPushConsumer延迟消息源码。 文章目录1 load加载延迟消息数据1.1 parseDelayLevel解析延迟等级2 start启动调度消息服务3 DeliverDelayedMessageTimerTask投递延迟消息任务3.1 executeOnTimeup执行延迟消息投递3.2…...
计算机视觉知识点(一)——交并比(IoU)及其若干改进
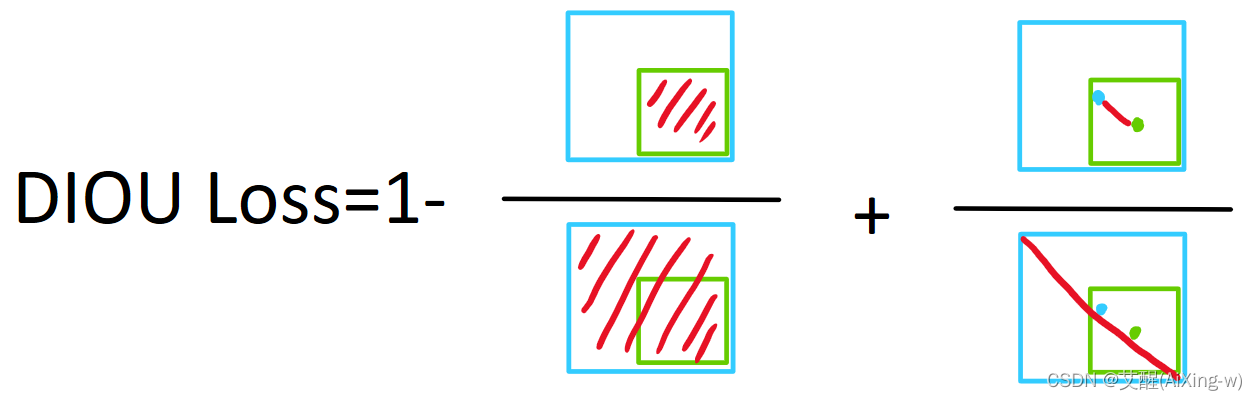
交并比(IoU)前言IoU公式及示意图IoU Loss缺点GIoU Loss公式及示意图缺点DIoU公式及示意图CIoU前言 目标检测是一个常见的计算机视觉任务,在目标检测任务中,交并比作为评判检测框的标准具有很重要的意义,在实际的应用中…...

一篇文章教你从零到一搭建自动化测试框架(附视频教程+源码)
目录 前言 1. 什么是自动化测试框架? 2. 没有万能的测试框架,适合自己项目的,能提高工作效率的就是好框架。 3. 设计框架的思路: 4.如何开展自动化测试 前言 关于测试框架的好处,比如快速回归提高测试效率&#x…...

【备战蓝桥杯】----01背包问题(动态规划)
🌹作者:云小逸 📝个人主页:云小逸的主页 📝Github:云小逸的Github 🤟motto:要敢于一个人默默的面对自己,强大自己才是核心。不要等到什么都没有了,才下定决心去做。种一颗树,最好的时间是十年前…...

Golang1.18新特性介绍——泛型
社区长期高呼的泛型特性在Golang 1.18中终于正式发布,Go泛型实现与传统的C有较大差异,更像Rust的泛型实现。本文详细介绍Golang泛型及其特性,包括泛型语法、类型参数、类型约束、类型近似以及constraints包提供内置类型等。 最近写Dao代码&am…...
【SpringBoot17】SpringBoot中使用Quartz管理定时任务
定时任务在系统中用到的地方很多,例如每晚凌晨的数据备份,每小时获取第三方平台的 Token 信息等等,之前我们都是在项目中规定这个定时任务什么时候启动,到时间了便会自己启动,那么我们想要停止这个定时任务的时候&…...

杨辉三角形 (蓝桥杯) JAVA
目录题目描述:暴力破解(四成):二分法破解(满分):题目描述: 下面的图形是著名的杨辉三角形: 如果我们按从上到下、从左到右的顺序把所有数排成一列,可以得到如…...

AI制药 - AlphaFold Multimer 的 MSA Pairing 源码
目前最新版本是v2.3.1,2023.1.12 AlphaFold multimer v1 于 2021 年 7 月发布,同时发表了一篇描述其方法和结果的论文。AlphaFold multimer v1 使用了与 AlphaFold 单体相同的模型结构和训练方法,但增加了一些特征和损失函数来处理多条链。Al…...

TitanIDE:云原生开发到底强在哪里?
原文作者:行云创新技术总监 邓冰寒 引言 是一种新的软件开发方法,旨在构建更可靠、高效、弹性、安全和可扩展的应用程序。与传统的应用程序开发方式不同,云原生是将开发环境完全搬到云端,构建一站式的云原生开发环境。云原生的开…...

单片机常用完整性校验算法
一、前言 单片机在开发过程中经常会遇到大文件传输,或者大量数据传输,在一些工业环境下,数据传输并不是很稳定,如何检验数据的完整性就是个问题,这里简单介绍一下单片机常用的几种数据完整性校验方法。 二、CheckSum校…...
Anaconda 的安装配置及依赖项的内外网配置
在分享anaconda 的安装配置及使用前,我们必须先明白anaconda是什么;Anaconda是一个开源的Python发行版本。两者区别在于前者是一门编程语言,后者相当于编程语言中的工具包。 由于python自身缺少numpy、matplotlib、scipy、scikit-learn等一系…...
p84 CTF夺旗-PHP弱类型异或取反序列化RCE
数据来源 文章参考 本课重点: 案例1:PHP-相关总结知识点-后期复现案例2:PHP-弱类型对比绕过测试-常考点案例3:PHP-正则preg_match绕过-常考点案例4:PHP-命令执行RCE变异绕过-常考点案例5:PHP-反序列化考题…...

2022财报逆转,有赞穿透迷雾实现突破
2022年,商家经营面临困难。但在一些第三方服务商的帮助下,也有商家取得了逆势增长。 2023年3月23日,有赞发布2022年业绩报告,它帮助许多商家稳住了一整年的经营。2022年,有赞门店SaaS业务的GMV达到425亿元,…...

蓝桥杯 - 求组合数【C(a,b)】+ 卡特兰数
文章目录💬前言885. 求组合数 I C(m,n) 【dp】886 求组合数 II 【数据大小10万级别】 【费马小定理快速幂逆元】887. 求组合数 III 【le18级别】 【卢卡斯定理 逆元 快速幂 】888.求组合数 IV 【没有%p -- 高精度算出准确结果】 【分解质因数 高精度乘法 --只用一…...

膳食真菌在癌症免疫治疗中的作用: 从肠道微生物群的角度
谷禾健康 癌症是一种恶性肿瘤,它可以发生在人体的任何部位,包括肺、乳房、结肠、胃、肝、宫颈等。根据世界卫生组织的数据,全球每年有超过1800万人被诊断出患有癌症,其中约有1000万人死于癌症。癌症已成为全球范围内的主要健康问题…...

怎么将模糊的照片变清晰
怎么将模糊的照片变清晰?珍贵的照片每个人都会有,而遇到珍贵的照片变模糊了,相信会让人很苦恼的。那么有没有办法可以解决呢?答案是有的,我们可以用工具让模糊的照片变得清晰。下面就来分享一些让模糊的照片变清晰的方法,有兴趣…...
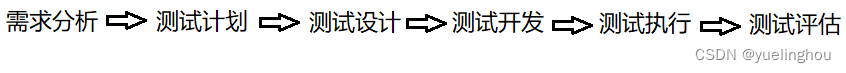
【软件测试】基础知识第一篇
文章目录一. 什么是软件测试二. 测试和调试的区别三. 什么是测试用例四. 软件的生命周期五. 软件测试的生命周期一. 什么是软件测试 软件测试就是验证软件产品特性是否满足用户的需求。 那需求又是什么呢?在多数软件公司,会有两种需求,一种…...

【百面成神】java web基础7问,你能坚持到第几问
前 言 🍉 作者简介:半旧518,长跑型选手,立志坚持写10年博客,专注于java后端 ☕专栏简介:纯手打总结面试题,自用备用 🌰 文章简介:java web最基础、重要的8道面试题 文章目…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...
