AI基础 L9 Local Search II 局部搜索
Local Beam search
对于当前的所有k个状态,生成它们的所有可能后继状态。
检查生成的后继状态中是否有任何状态是解决方案。
如果所有后继状态都不是解决方案,则从所有后继状态中选择k个最佳状态。
当达到预设的迭代次数或满足某个终止条件时,算法停止。
— Choose k successors randomly, biased towards good ones
— Close analogy to natural selection

Genetic Algorithms
遗传算法的一些关键特征:
-
随机局部光束搜索:
- 定义:遗传算法通过随机局部光束搜索来生成解决方案。
- 作用:这有助于算法探索状态空间,并找到更好的解决方案。
-
从状态对生成后继状态:
- 定义:遗传算法通过交叉操作,从两个父代状态生成新的子代状态。
- 作用:这有助于算法在种群中传播有用的信息,并产生新的解决方案。
-
状态表示:
- 定义:每个状态应该是一个字符串,其中字符串的子串应该有意义。
- 作用:这有助于算法有效地表示和操作解决方案。
-
应用示例:
- 定义:n-皇后问题是一个典型的遗传算法应用示例。
- 作用:在这个问题中,每个状态用一个字符串表示,其中第i个字符表示第i个皇后所在的行。
• Population of individuals 一组可能的解决方案
• Mutation — local search N (x) 变异是指对种群中的个体进行小的随机改变。
• cross over — population holds information 交叉是指将两个父代个体的部分基因组合在一起,形成新的子代个体。
• generations — iterations of improvement 代是指遗传算法中迭代的过程。
GA Terminology
• Gene - characters in the string representing the state
• Chromosome - blocks of genes in the string in a state
• Population - neighbours in the search
• Selection, crossover, mutation
1-point crossover
随机选择切点 交换切割后的尾部
Create children by exchanging tails (typically with 0.6 < PC < 0.9)

n-point crossover
随机选择n个切点 交替交换切割后的尾部
• Glue parts, alternating between parents
• Generalisation of 1 point (still some positional bias)
指的是多点交叉相对于单点交叉的推广。虽然多点交叉通过选择多个交叉点来减少位置偏见,但仍然存在一定的位置偏见,因为交叉点的位置会影响子代个体的基因组合。这意味着,尽管多点交叉减少了位置偏见,但仍然不能完全消除位置对交叉结果的影响。

uninform crossover
• Assign ‘heads‘ to one parent, ‘tails‘ to the other
• Flip a coin for each gene of the first child
• Make an inverse copy of the gene for the second child
• Inheritance is independent of position 遗传与位置无关
按照50%概率为每个个体分配切割后的头部和尾部 切割成最小不可分单位

mutation
• Alter each gene independently with a probability Pm
• Pm is called the mutation rate
• Typically between 1/pop_size and 1/chromosome_length
每一个最小不可分部分按突变率发生变化
Selection
• Main idea: better individuals get higher chance
• Chances proportional to fitness
• Implementation: roulette wheel technique
— Assign to each individual a part of the roulette wheel
— Spin the wheel n times to select n individuals
 加权选择
加权选择
Crossover VS. mutation
• Exploration: Discovering promising areas in the search space, i.e. gaining information
on the problem 通常用于探索新的解决方案
• Exploitation: Optimising within a promising area, i.e. using information 用于在当前解决方案的基础上进行微调
• There is co-operation and competition between them
— Crossover is explorative, it makes a big jump to an area somewhere “in between“ two
(parent) areas
— Mutation is exploitative, it creates random small diversions, thereby staying near (in the
area of) the parent
• Only crossover can combine information from two parents crossover合并父级信息
• Only mutation can introduce new information (alleles) mutation 产生新信息
• Crossover does not change the allele frequencies of the population crossover不会改变信息频率
• To hit the optimum you often need a ‘lucky‘ mutation mutation达到最佳需要运气

Continuous state spaces

适用于那些需要找到全局最优解或近似最优解的问题。它的主要优点是能够找到全局最优解或近似最优解,但它的主要缺点是可能需要大量的迭代次数。
相关文章:

AI基础 L9 Local Search II 局部搜索
Local Beam search 对于当前的所有k个状态,生成它们的所有可能后继状态。 检查生成的后继状态中是否有任何状态是解决方案。 如果所有后继状态都不是解决方案,则从所有后继状态中选择k个最佳状态。 当达到预设的迭代次数或满足某个终止条件时&#x…...

828华为云征文|使用sysbench对Mysql应用加速测评
文章目录 ❀前言❀测试环境准备❀测试工具选择❀测试工具安装❀mysql配置❀未开启Mysql加速测试❀开启Mysql加速测试❀总结 ❀前言 大家好,我是早九晚十二。 昨天有梳理一篇关于华为云最新推出的云服务器产品Flexus云服务器X。当时有说过,这次的华为云F…...

2024 年高教社杯全国大学生数学建模竞赛题目——D 题 反潜航空深弹命中概率问题的求解
2024 年高教社杯全国大学生数学建模竞赛题目 (请先阅读“ 全国大学生数学建模竞赛论文格式规范 ”) D 题 反潜航空深弹命中概率问题 应用深水炸弹(简称深弹)反潜,曾是二战时期反潜的重要手段,而随着现代军…...
)
【Kubernetes】常见面试题汇总(一)
目录 1.简述 etcd 及其特点? 2.简述 etcd 适应的场景? 3.简述什么是Kubernetes? 4.简述 Kubernetes和 Docker的关系? 1.简述 etcd 及其特点? (1)etcd 是Core0s 团队发起的开源项目…...

简单实用的php全新实物商城系统
免费开源电商系统,提供灵活的扩展特性、高度自动化与智能化、创新的管理模式和强大的自定义模块,让电商用户零成本拥有安全、高效、专业的移动商城。 代码是全新实物商城系统源码版。 代码下载...

Leetcode面试经典150题-128.最长连续序列-递归版本另解
之前写过一篇这个题的,但是可能代码比较复杂,这回来个简洁版的,这个是递归版本 可以看看之前的版本,两个版本面试用哪个都保过 解法都在代码里,不懂就留言或者私信 class Solution {/**对于之前的解法,我…...

spring security 中的授权使用
一、认证 身份认证,就是判断一个用户是否为合法用户的处理过程。Spring Security 中支持多种不同方式的认证,但是无论开发者使用那种方式认证,都不会影响授权功能使用。因为 SpringSecurity 很好做到了认证和授权解耦。 二、授权 授权&#x…...
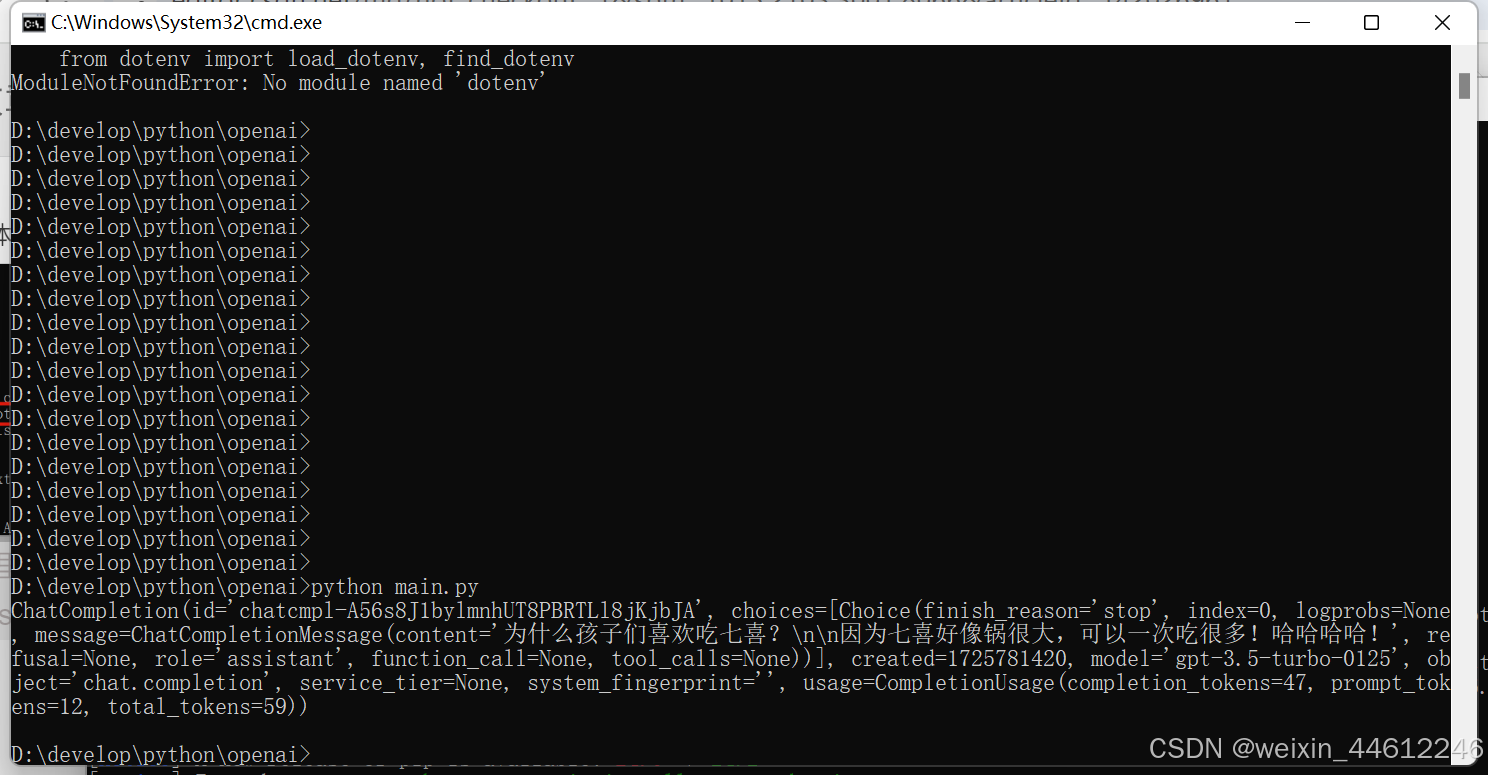
python安装以及访问openAI API
安装python 我是python小白,所以需要一步一步来,先安装。 一口吃不成胖子,记住。 从官网下载python,目前最新版本是3.12,但是据说稳定版3.11更好一点,所以,下载3.11,注意不要下载…...

【Unity小技巧】URP管线遮挡高亮效果
前言 在URP渲染管线环境下实现物体遮挡高亮显示效果,效果如下:Unity URP遮挡高亮 实现步骤 创建层级,为需要显示高亮效果的物体添加层级,比如Player 创建一个材质球,也就是高亮效果显示的材质球找到Universal Render…...
图形设备接口)
C#中的GDI和GDI+(Graphics Device Interface Plus)图形设备接口
GDI的概念 GDI(Graphics Device Interface)是微软Windows操作系统中的一个组件,它提供了一组API,用于在显示器或打印机等图形设备上进行图形绘制和图像处理。GDI 是 Windows 编程中用于二维图形和图像处理的接口。 GDI 的主要功…...

谷粒商城のNginx
文章目录 前言一、Nginx1、安装Nginx2、相关配置2.1、配置host2.2、配置Nginx2.3、配置网关 前言 本篇重点介绍项目中的Nginx配置。 一、Nginx 1、安装Nginx 首先需要在本地虚拟机执行: mkdir -p /mydata/nginx/html /mydata/nginx/logs /mydata/nginx/conf在项目…...

Debug-027-el-tooltip组件的使用及注意事项
前言: 这两天,碰到这个饿了么的el-tooltip比较多。这个组件使用起来也挺简单的,常用于展示鼠标 hover 时的提示信息。但是有一些小点需要注意。这里不再机械化的介绍文档,不熟悉的话可以先看一下: https://element-pl…...

猫眼电影字体破解(图片转码方法)
问题 随便拿一篇电影做样例。我们发现猫眼的页面数据在预览窗口中全是小方框。在当我们拿到源码以后,数据全是加密后的。所以我们需要想办法破解加密,拿到数据。 破解过程 1.源码获取问题与破解 分析 在我们刚刚请求url的时候是可以得到数据的ÿ…...

flink wordcount
Maven配置pom文件 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/P…...
)
组合模式(Composite Pattern)
使用组合模式(Composite Pattern)是一个更优雅的方式来表示菜单和菜单项。组合模式允许我们将单个对象(如菜单项)和组合对象(如菜单)以相同的方式处理。 解决方案: 创建组合结构:我…...
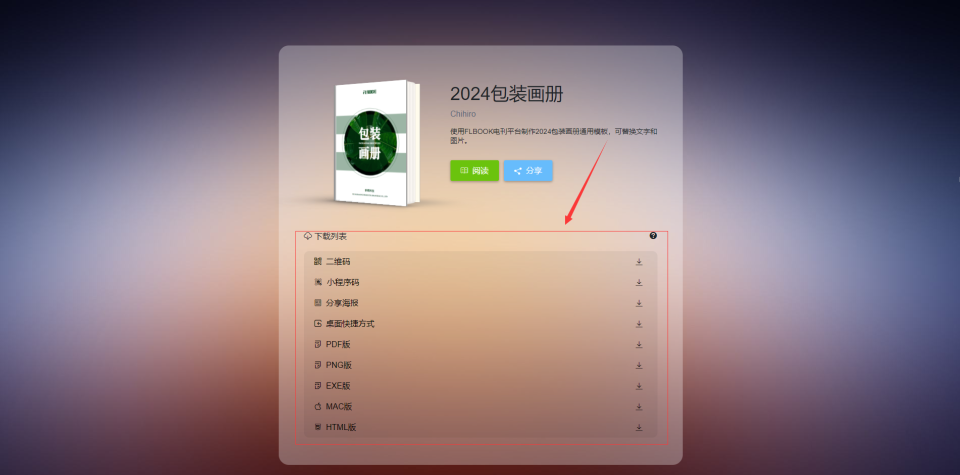
教你制作一本加密的样本册
在这个信息的时代,保护自己的隐私和知识产权变得尤为重要。你有没有想过,如何将自己珍贵的样本资料变成一本只有自己才能查看的加密宝典?今天,我就来教你制作一本加密的样本册 第一步,打开浏览器,搜索FLBOO…...

C语言进阶【1】--字符函数和字符串函数【1】
本章概述 字符分类函数字符转换函数strlen的使用和模拟实现strcpy的使用和模拟实现strcat的使用和模拟实现strcmp的使用和模拟实现彩蛋时刻!!! 字符分类函数 字符: 这个概念,我们在以前的文章中讲过了。我们键盘输入的…...

git提交自动带上 Signed-off-by信息
为了确保在使用 Signed-off-by 签名的同时保留你的提交消息,你需要修改 prepare-commit-msg 钩子脚本,以便它不会丢失原始的提交信息。 增加prepare-commit-msg 钩子以保留提交消息 prepare-commit-msg 钩子的目的是在提交信息文件中插入额外的内容&am…...

图论(2)
一、度 度统计的是一个节点上又多少条边 度出度入度 出度:统计以该节点为起始点箭头指向外面的边的条数 入度:统计箭头指向该节点的边数 度为1的节点为悬挂节点,边为悬挂边 用矩阵计算节点的度 二、握手定理 比如这里第一个集合里面有三…...

ASP.NET Core 入门教学十九 依赖注入ioc
ASP.NET Core内置了对依赖注入(Dependency Injection,简称DI)的支持,这是一种设计模式,用于实现控制反转(Inversion of Control,简称IoC),从而使得应用程序组件之间的耦合…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
