数学建模拓展内容:卡方检验和Fisher精确性检验(附有SPSS使用步骤)
卡方检验和Fisher精确性检验
- 卡方拟合度检验
- 卡方独立性检验
- 卡方检验的前提假设
- Fisher精确性检验
卡方拟合度检验
卡方拟合度检验概要:卡方拟合度检验也被称为单因素卡方检验,用于检验一个分类变量的预期频率和观察到的频率之间是否存在显著差异。
卡方拟合度检验举例分析:例如将一个六个面的骰子投掷36次可以得到不同点数的出现频数。在正常情况下,各个点数的出现频率应该大致相等,如果通过卡方拟合度检验判断实际频率和预期频率确实存在显著差异,那么我们就有理由认为骰子本身存在问题。
卡方独立性检验
卡方独立性检验概要:卡方独立性检验也被称为双因素卡方检验,用于检验两个类别变量之间是否相互独立。
交叉表:
- 交叉表作用:当同一个个体可以被以两种划分方式分为两种类别时,可以通过交叉表进行直观的类别判定。
- 交叉表样例:可以将一个总体人群中的人按照性别分为男性和女性,所有人按照啤酒嗜好又可以分为喜欢淡啤酒、喜欢普通啤酒、喜欢黑啤酒三类。也就是说,对于原始人群,可以分别按照两种方式进行分类,而交叉表就是综合两种分类结果的直观展示,原始数据和对应的交叉表如下所示:(表格中的性别和啤酒嗜好都已经转换为了虚拟变量)
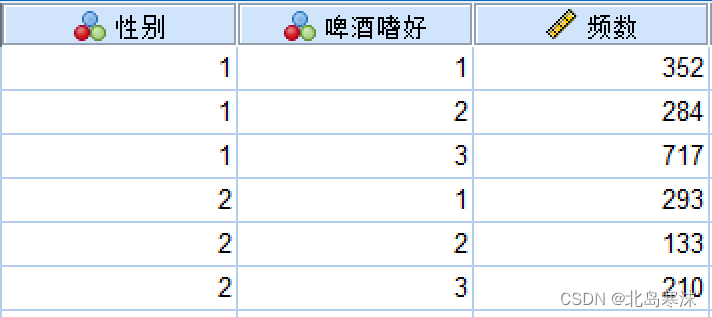
使用SPSS绘制交叉表和进行卡方独立性检验:
-
导入原始数据后依次点击:
数据→个案加权。
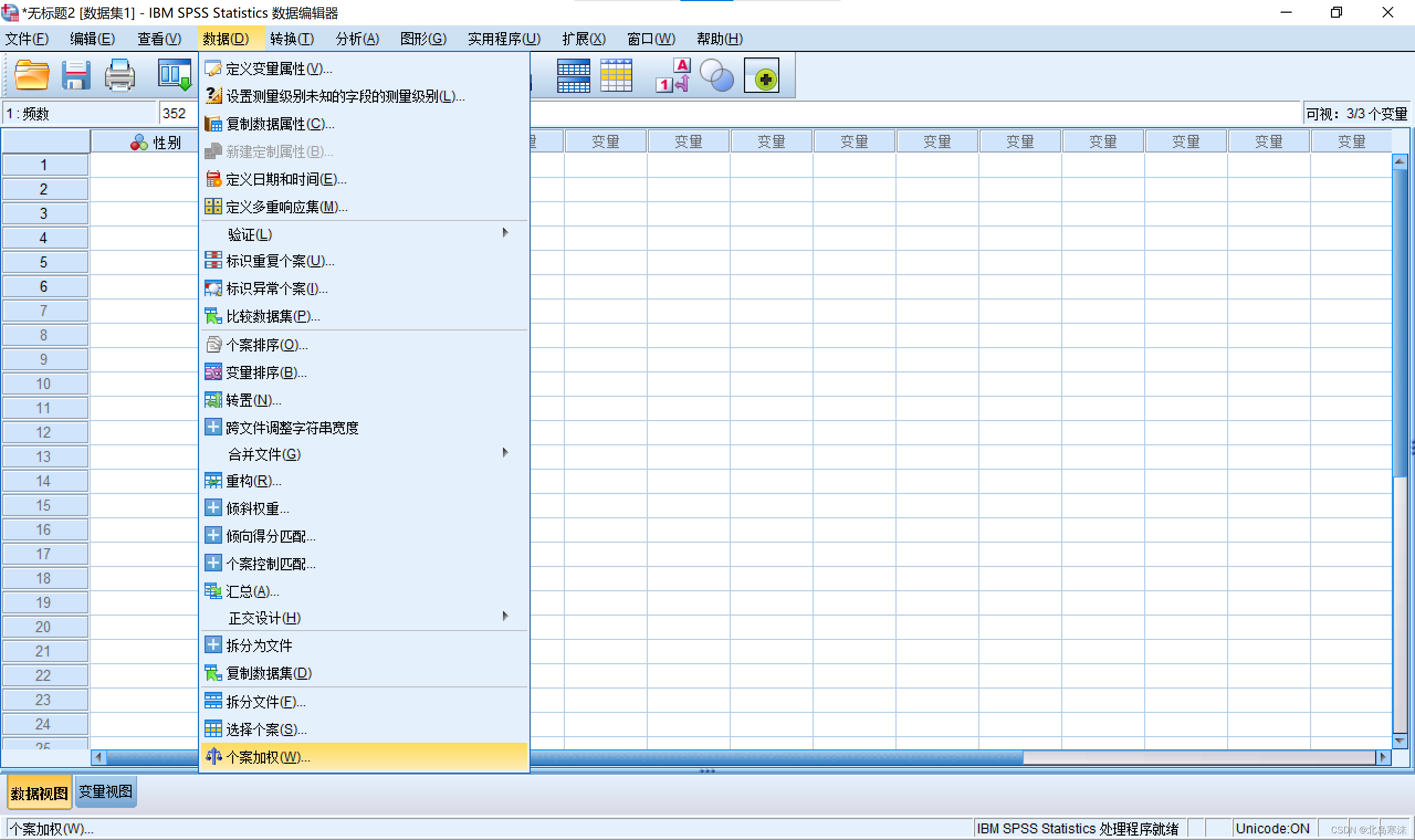
-
选择
个案加权系数,将频数作为个案加权系数后点击确定。
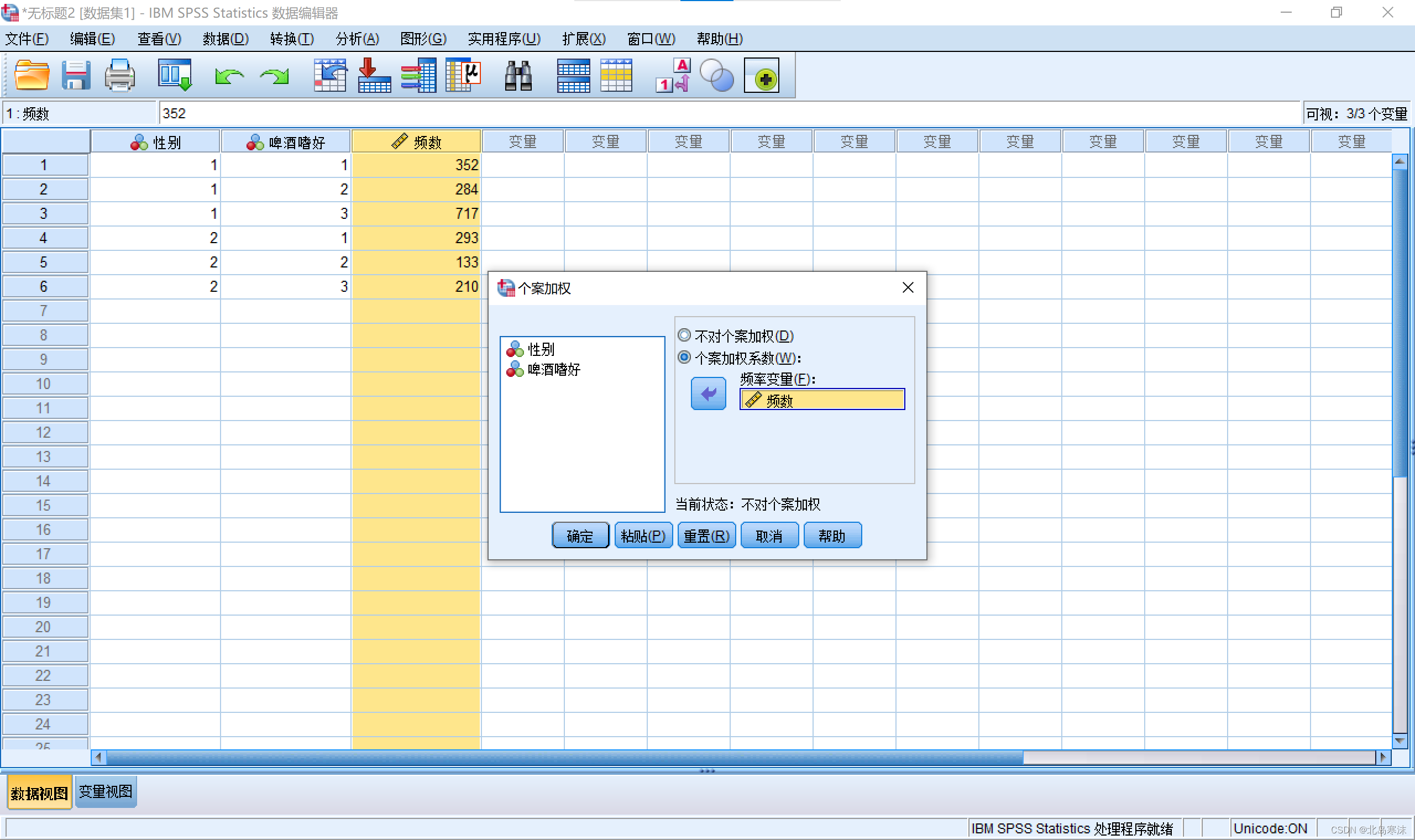
-
依次点击:
分析→描述统计→交叉表。
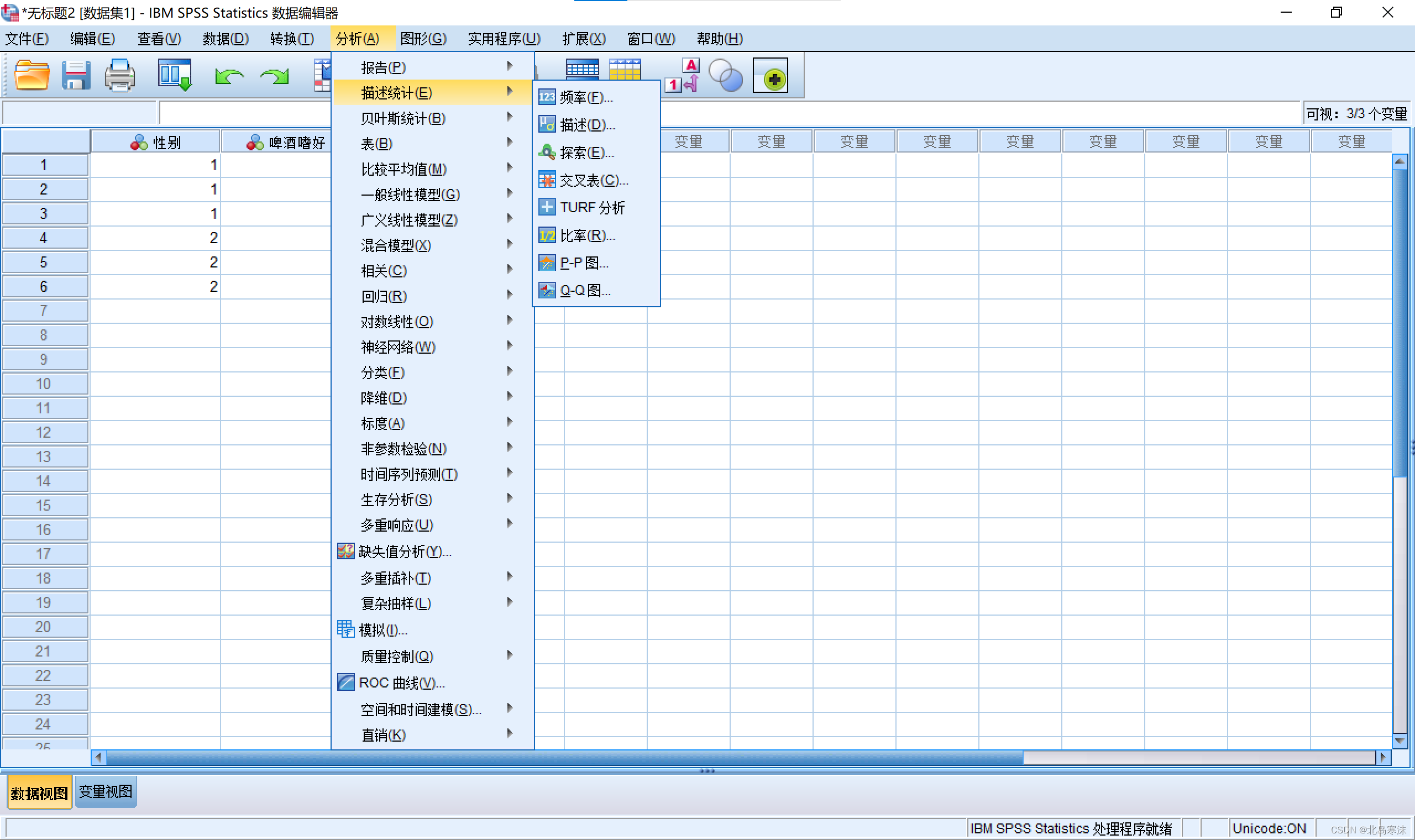
-
选择两个指定的类别变量作为交叉表的行和列,并在窗口左下角勾选
显示簇状条形图。
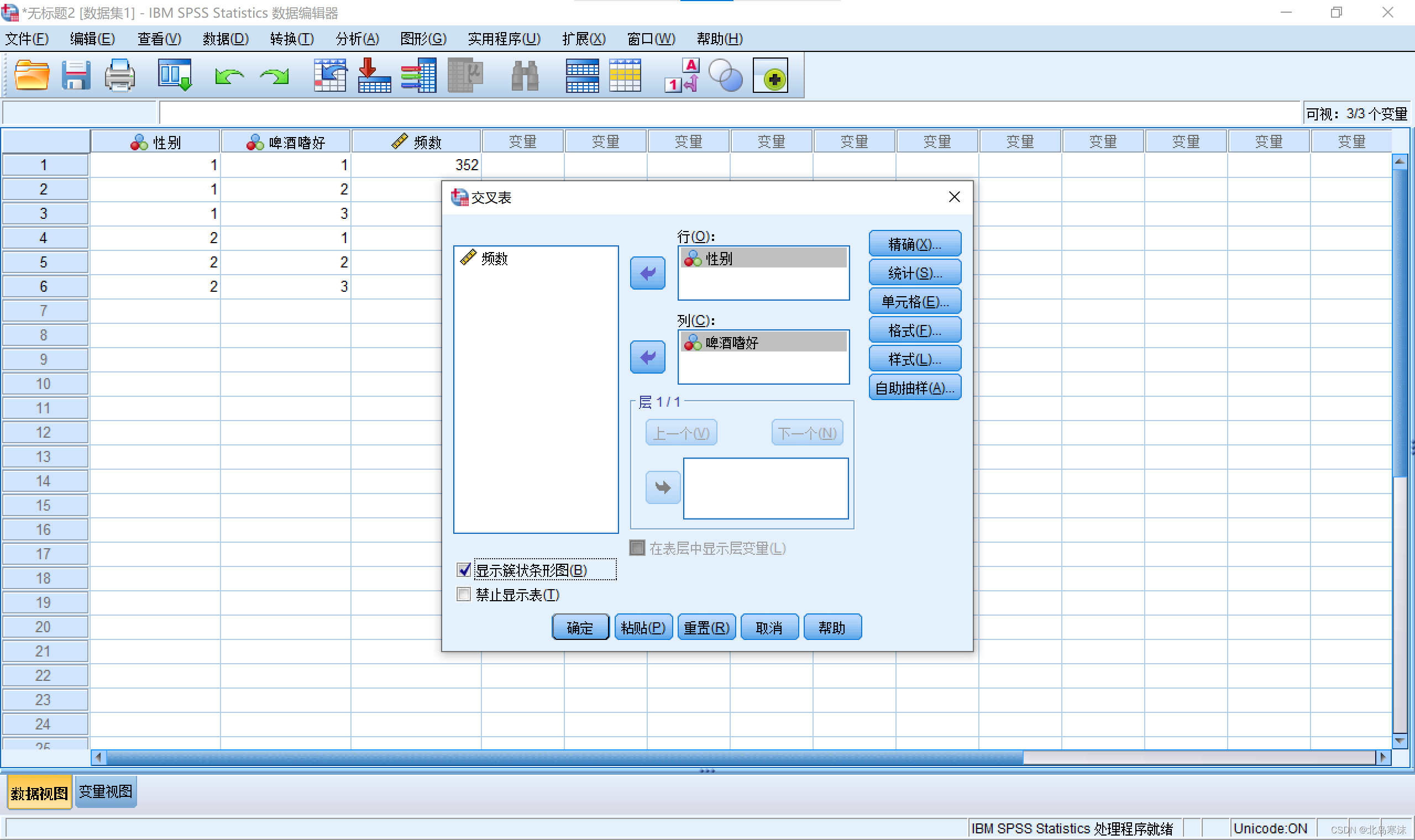
-
打开
精确窗口,选择精确。
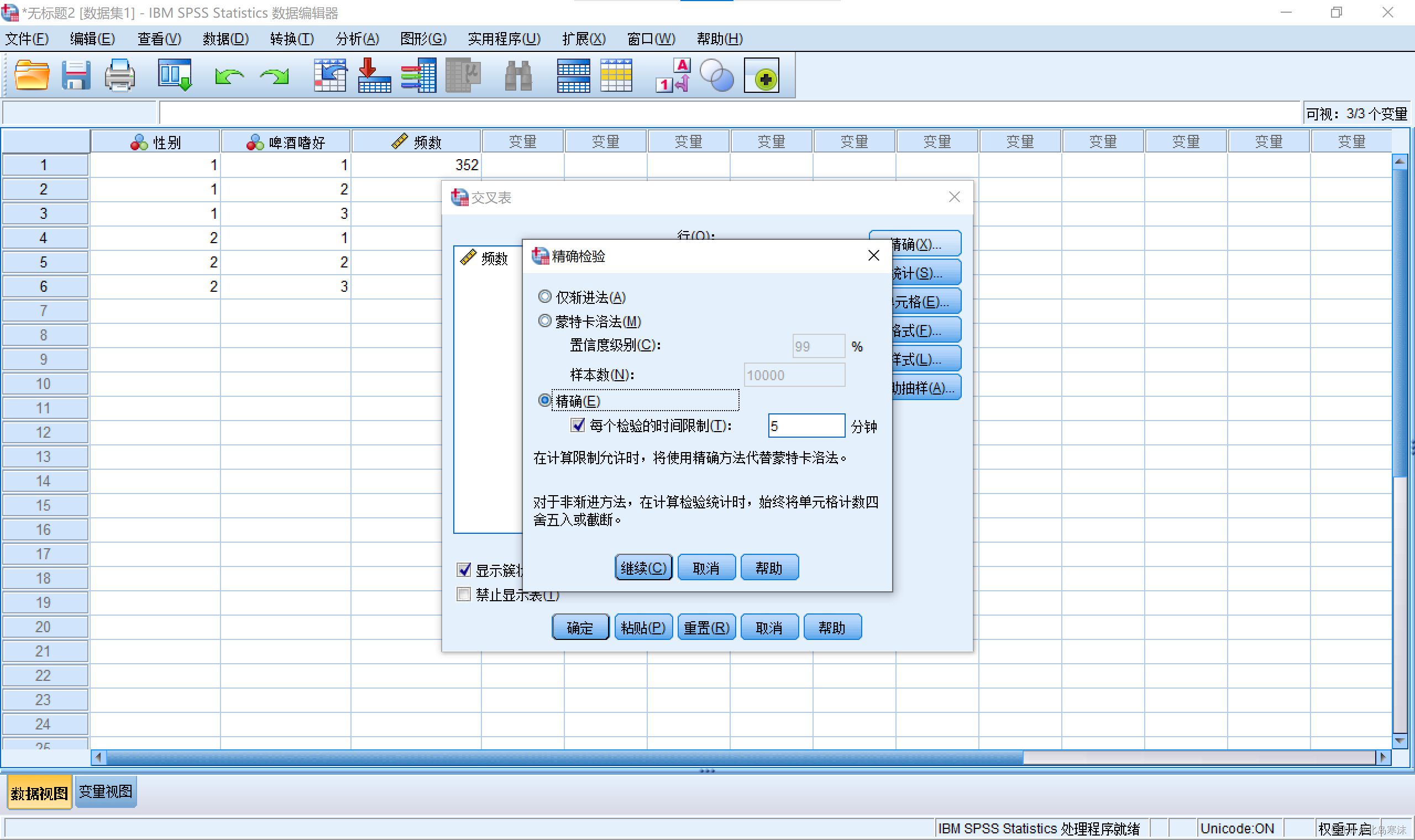
-
打开
统计窗口,选择卡方。
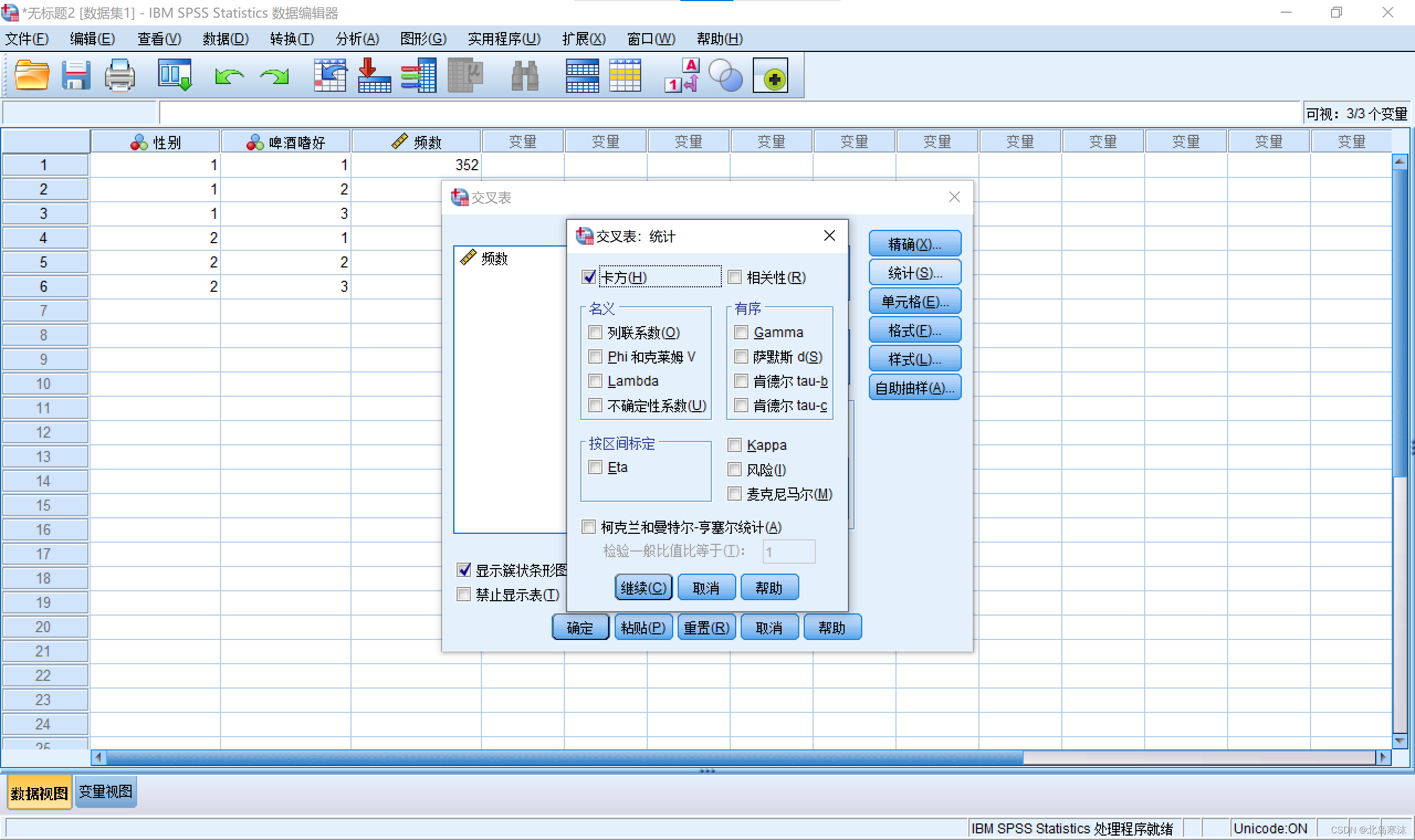
-
单击
确定。
SPSS进行卡方独立性检验的结果分析:
- 交叉表:
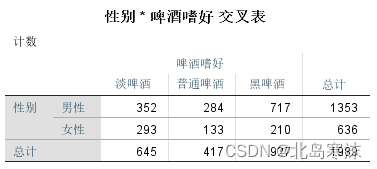
- 卡方独立性检验结果:
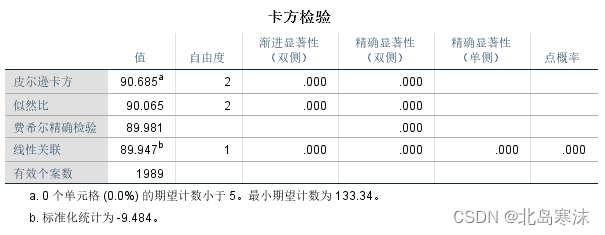
这里的渐近显著性和精确显著性即对应的P值,一般看渐近显著性。如果渐近显著性的值小于给定的显著性水平,那么就认为两个分类变量之间不是相互独立的。
一般只需要判定皮尔逊卡方结果的渐近显著性即可。在大样本情况下,皮尔逊卡方和似然比检验的结果会比较接近。 - 条形图:
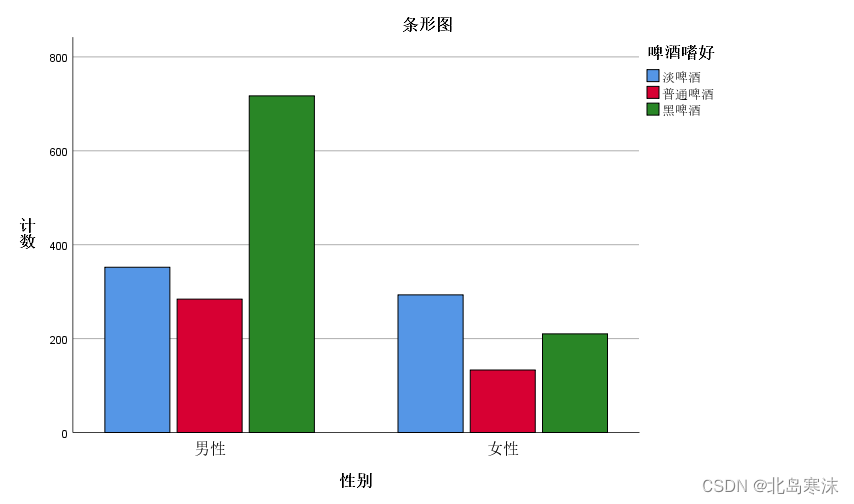
卡方检验的前提假设
- 每个观测值都会落入一个,且只能落入一个类别中。
- 每个观测值之间相互独立。
- 卡方独立性检验的适用情况:最好在样本个数大于40,且每个类别的期望频数都大于等于5时才使用卡方独立性检验。
Fisher精确性检验
Fisher精确性检验概述:Fisher精确性检验的作用与卡方独立性检验类似,但是适用于小样本的情况,在卡方独立性检验不满足适用条件时可以采用Fisher精确性检验。
Fisher精确性检验的适用情况:超过20%的交叉表元素的期望值小于5或者至少存在一个交叉表元素的期望值小于1。
SPSS进行Fisher精确性检验的结果:

Fisher精确性检验的结果也在卡方独立性检验的结果表格中。表格的第三行费希尔精确性检验即为进行Fisher精确性检验的结果。
相关文章:

数学建模拓展内容:卡方检验和Fisher精确性检验(附有SPSS使用步骤)
卡方检验和Fisher精确性检验卡方拟合度检验卡方独立性检验卡方检验的前提假设Fisher精确性检验卡方拟合度检验 卡方拟合度检验概要:卡方拟合度检验也被称为单因素卡方检验,用于检验一个分类变量的预期频率和观察到的频率之间是否存在显著差异。 卡方拟…...

【Python学习笔记之七大数据类型】
Python数据类型:Number数字、Boolean布尔值、String字符串、list列表、tuple元组、set集合、dictionary字典 int整数 a1 print(a,type(a))float浮点数 b1.1 print(b,type(b))complex复数 c100.5j print(c,type(c))bool布尔值:True、False,true和false并非Python…...

Android系统之onFirstRef自动调用原理
前言:抽丝剥茧探究onFirstRef究竟为何在初始化sp<xxx>第一个调用?1.onFirstRef调用位置<1>.system/core/libutils/RefBase.cpp#include <utils/RefBase.h>//1.初始化强指针 void RefBase::incStrong(const void* id) const {weakref_i…...
ipv6上网配置
一般现在的宽带都已经支持ipv6了,但是需要一些配置才能真正用上ipv6。记录一下配置过程。 当前测试环境为移动宽带,光猫下面接了一个路由器,家里所有的设备都挂到这个路由器下面的。 1. 光猫改桥接 光猫在使用路由模式下,ipv6无…...

python实现聚类技术—复杂网络社团检测 附完整代码
实验内容 某跆拳道俱乐部数据由 34 个节点组成,由于管理上的分歧,俱乐部要分解成两个社团。 该实验的任务即:要求我们在给定的复杂网络上检测出两个社团。 分析与设计 实验思路分析如下: 聚类算法通常可以描述为用相似度来衡量两个数据的远近,搜索可能的划分方案,使得目标…...
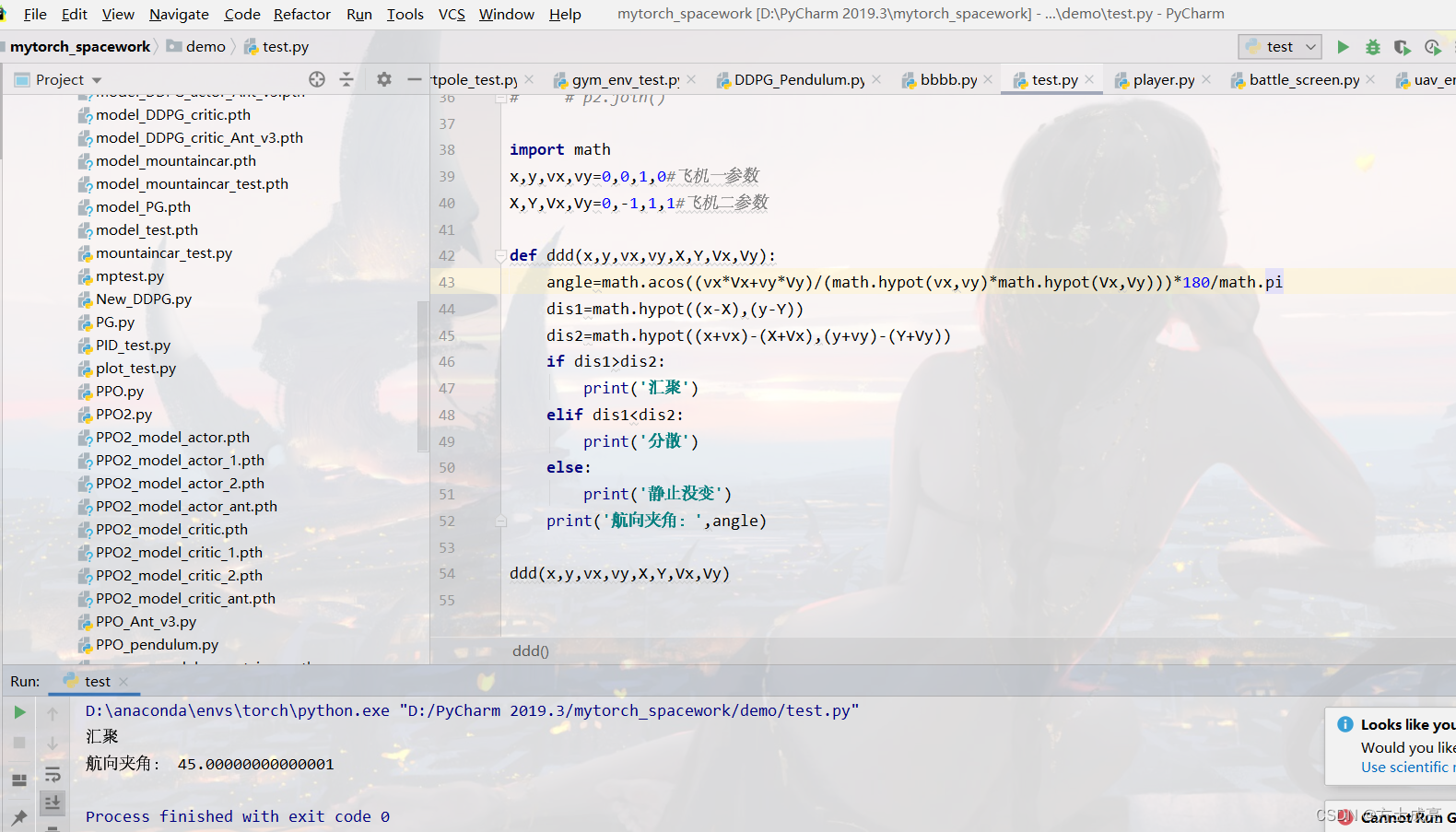
如何判断两架飞机在汇聚飞行?(如何计算两架飞机的航向夹角?)内含程序源码
ok,在开始一切之前,让我先猜一猜,你是不是想百度“二维平面下如何计算两个移动物体的航向夹角?”如果是,那就请继续往下看。 首先,我们要明确一个概念:航向角≠航向夹角!࿰…...

Scipy稀疏矩阵bsr_array
文章目录基本原理初始化内置方法基本原理 bsr,即Block Sparse Row,bsr_array即块稀疏行矩阵,顾名思义就是将稀疏矩阵分割成一个个非0的子块,然后对这些子块进行存储。通过输入维度,可以创建一个空的bsr数组࿰…...

LeetCode笔记:Weekly Contest 332
LeetCode笔记:Weekly Contest 332 1. 题目一 1. 解题思路2. 代码实现 2. 题目二 1. 解题思路2. 代码实现 3. 题目三 1. 解题思路2. 代码实现 4. 题目四 1. 解题思路2. 代码实现 比赛链接:https://leetcode.com/contest/weekly-contest-332/ 1. 题目一…...

autox.js在vscode(win7)与雷神模拟器上的开发环境配置
目录 下载autox.js 安装autox.js? 在电脑上搭建autox.js开发环境 安装vscode 安装autox.js插件 雷神模拟器连接vscode 设置雷神模拟器IP 设置autox.js应用IP地址等 下载autox.js 大体来说,就是一个运行在Android平台上的JavaScript 运行环境 和…...

创建阿里云物联网平台
创建阿里云物联网平台 对云平台设备创建过程做记录,懒得再看视频 文章参考视频:https://www.bilibili.com/video/BV1jP4y1E7TJ?p26&vd_source50694678ae937a743c59db6b5ff46c31 阿里云:https://www.aliyun.com 1.物联网平…...
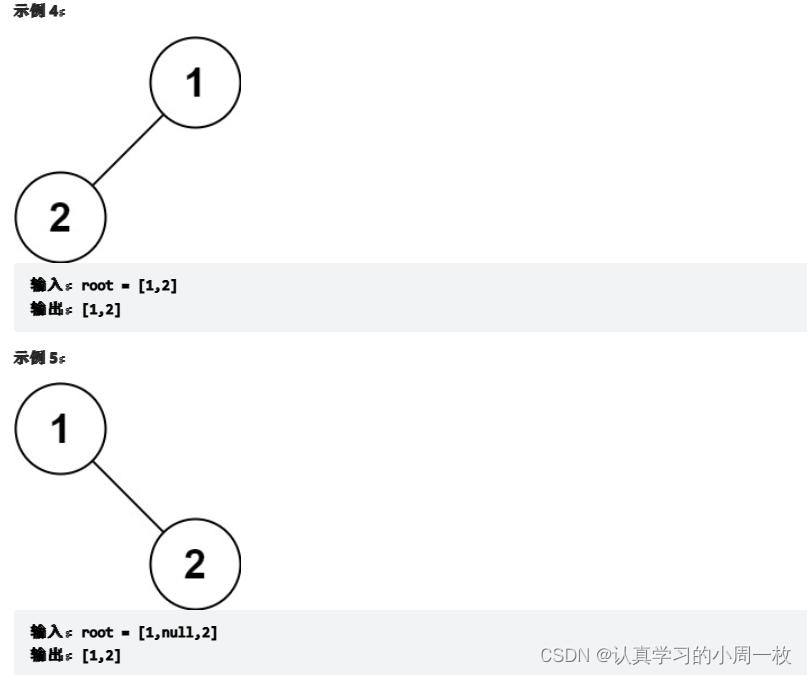
【链式二叉树】数据结构链式二叉树的(万字详解)
前言: 在上一篇博客中,我们已经详解学习了堆的基本知识,今天带大家进入的是二叉树的另外一种存储方式----“链式二叉树”的学习,主要用到的就是“递归思想”!! 本文目录1.链式二叉树的实现1.1前置说明1.2结…...

Koa2篇-简单介绍及使用
一.简介koa2是基于 Node.js 平台的下一代 web 开发框架, 致力于成为一个更小、更富有表现力、更健壮的 Web 框架。 可以避免异步嵌套. express中间件是异步回调,Koa2原生支持async/await二.async/awaitconst { rejects } require("assert"); const { resolve } req…...
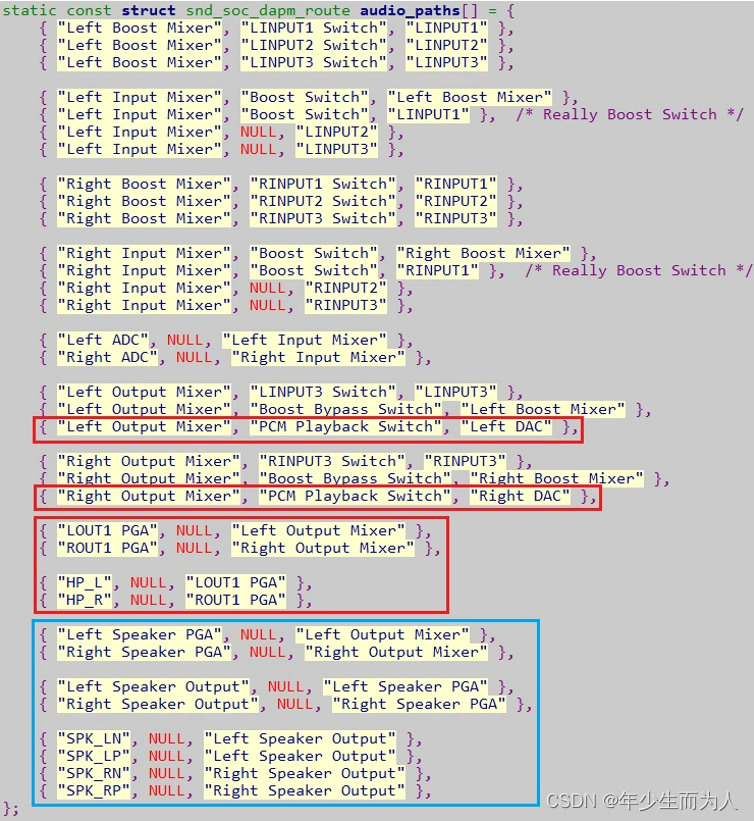
Linux ALSA 之十一:ALSA ASOC Path 完整路径追踪
ALSA ASOC Path 完整路径追踪一、ASoc Path 简介二、ASoc Path 完整路径2.1 tinymix 设置2.2 完整路径 route一、ASoc Path 简介 如前面小节所描述,ASoc 中 Machine Driver 是 platform driver 和 codec driver 的粘合剂,audio path 离不开 FE/BE/DAI l…...

【Spring Cloud总结】1、服务提供者与服务消费者快速上手
目录 文件结构 代码 1、api 1.1实体类(Dept ) 1.2数据库 2、provider 2.1 DeptController 2.2 DeptDao 2.3 DeptService 2.4 DeptServiceImpl 2.5 application.yml 3、consumer 3.1 ConfigBean 3.2 DeptConsumerController 测试 1.启动…...

若依项目学习之登录生成验证码
若依项目学习之登录生成验证码 使用DefaultKaptcha生成验证码 /*** 验证码配置* * author ruoyi*/ Configuration public class CaptchaConfig {/*** 生成字符类型的验证码**/Bean(name "captchaProducer")public DefaultKaptcha getKaptchaBean(){DefaultKaptcha…...
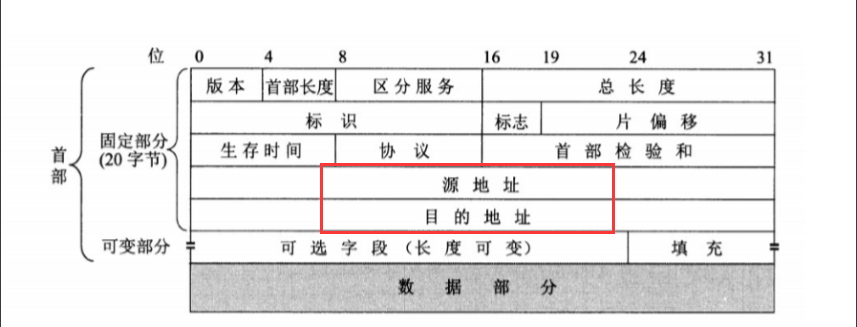
计算机网络5:数据在两台计算机之间是怎样传输的?
数据在两台计算机之间的传输总的来说包括了封装和解封两个过程 封装(5层协议) 以传送一张图片为例 **应用层:**将jpg格式的图片数据转化成计算机可以识别的0101的二进制的比特流 **传输层:**将应用层传输下来的数据进行分段&…...

就现在!为元宇宙和Web3对互联网的改造做准备!
欢迎来到Hubbleverse 🌍 关注我们 关注宇宙新鲜事 📌 预计阅读时长:8分钟 本文仅代表作者个人观点,不代表平台意见,不构成投资建议。 如今,互联网是各种不同的网站、应用程序和平台的集合。由于彼此分离…...
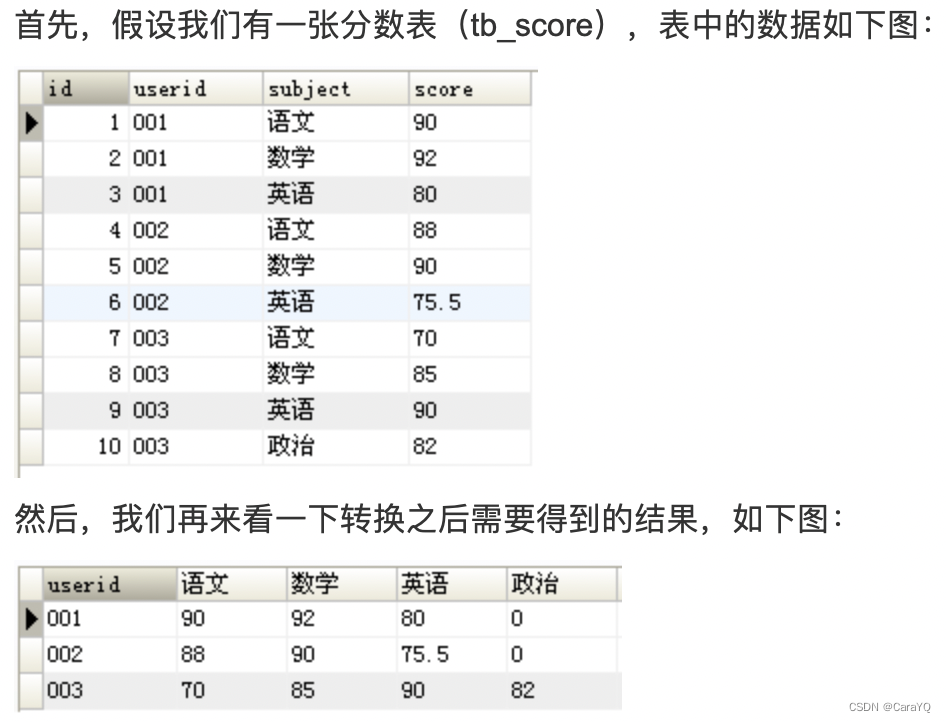
【mysql数据库】
目录SQL数据库分页聚合函数表跟表之间的关联关系SQL中怎么将行转成列SQL注入将一张表的部分数据更新到另一张表WHERE和HAVING的区别索引索引分类如何创建及保存MySQL的索引?怎么判断要不要加索引?索引设计原理只要创建了索引,就一定会走索引吗…...
【测试开发】web 自动化测试 --- selenium4
目录1. 什么是自动化为什么要做自动化2. 为什么选择selenium作为我使用的web自动化工具3. 什么是驱动?驱动的工作原理是什么5. 第一个自动化程序演示6. selenium基本语法6.1 定位元素的方法6.2 操作页面元素6.3 等待6.4 信息打印获取当前页面句柄,窗口切…...
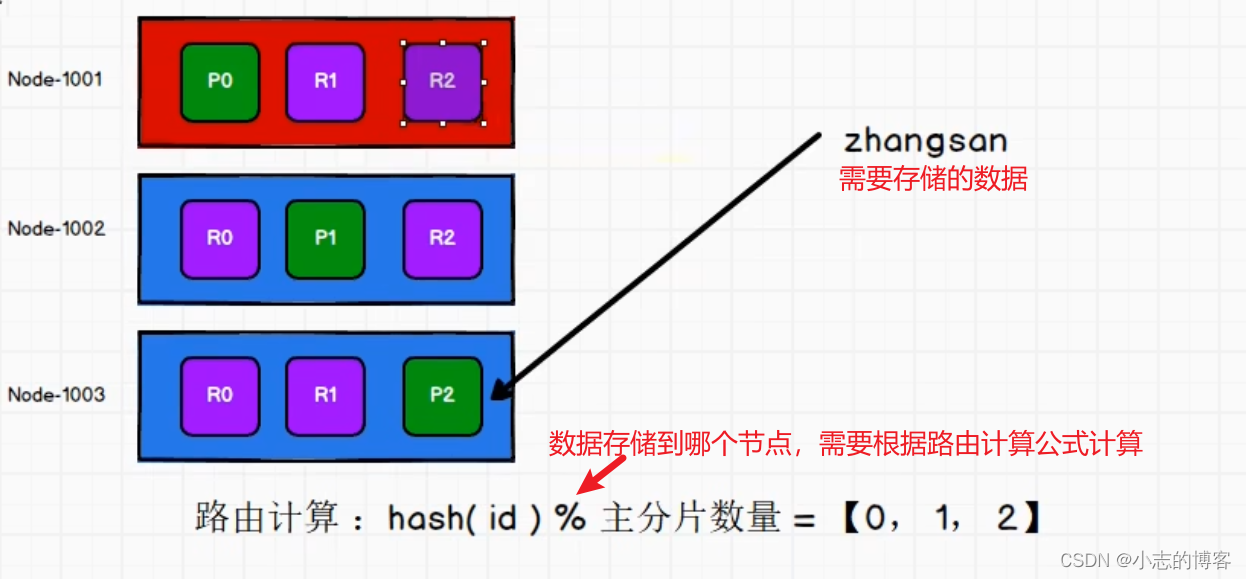
Elasticsearch7.8.0版本进阶——路由计算
目录一、路由计算1.1、路由计算的前提理解1.2、路由计算的概述1.3、路由计算的概述一、路由计算 1.1、路由计算的前提理解 当索引一个文档的时候,文档会被存储到一个主分片中。Elasticsearch 如何知道一个文档应该存放到哪个分片中呢?当我们创建文档时…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...
