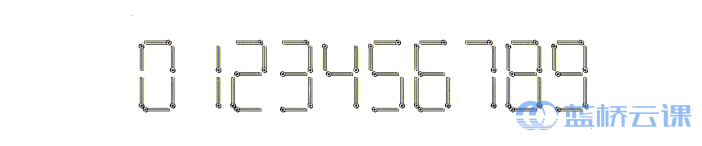蓝桥杯倒计时 | 倒计时17天
作者🕵️♂️:让机器理解语言か
专栏🎇:蓝桥杯倒计时冲刺
描述🎨:蓝桥杯冲刺阶段,一定要沉住气,一步一个脚印,胜利就在前方!
寄语💓:🐾没有白走的路,每一步都算数!🐾
题目一:22年省赛A题——小兰做实验 (难度:★★)
小蓝做实验 - 蓝桥云课 (lanqiao.cn)
问题描述
小蓝很喜欢科研, 他最近做了一个实验得到了一批实验数据, 一共是两百 万个正整数。
如果按照预期, 所有的实验数据 x 都应该满足
。但是做实验都会有一些误差, 会导致出现一些预期外的数据, 这种误差数据 y 的 范围是 1
。由于小蓝做实验很可靠, 所以他所有的实验数据中 99.99% 以上都是符合预期的。小蓝的所有实验数据都在 primes.txt 中, 现 在他想统计这两百万个正整
数中有多少个是质数, 你能告诉他吗?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
【思路】
三个考点:
- 读文件。文件有200万个整数,只能读文件,不能复制到代码中。
- 素数判断。判断x是否为素数,可以把它除以[2, sqrt(x)]内的素数,如果能整除,就不是素数。
- 素数筛,预处理出素数。文件里99.99%的整数都<
,所以只要得到
内的素数即可。约1300个素数。其他0.01%的大于
的数,数量很少,可以单独判断。
计算量:1300×200万。
Python代码实际运行时间:约1分钟。
【代码】
注意:在IDLE运行时,代码和文件必须在同一个文件夹内。
from math import *def E_sieve(n): # 得到10^4以内的素数for i in range (2,int (sqrt (n)+1)):if not vis[i]:for j in range(i*i, n+1,i):vis[j] =1k = 0 for i in range(2,n+1):#存素数if not vis[i]:prime[k] = ik += 1return kdef is_prime(x): # 判断素数:若n是素数,返回trueif x == 1: return False #1不是素数for i in range(k):if x % prime[i] == 0: return False #不是素数return True #是素数cnt = 0
N = int(1e4)
prime =[0]*N
vis =[0]*N
n = int(1e4)
k = E_sieve(n-1)
print(k) #质数个数
with open ('primes.txt','r') as f: # 读取文件for a in f:b=int(a.rstrip()) #去掉末尾的\n,转为整数if b<=int(1e8):if is_prime(b)==True:cnt +=1#else:#单独判断大于1e8的数字
print(cnt)
题目二:22年省赛B题——火柴棒数字 (难度:★★★)
火柴棒数字 - 蓝桥云课 (lanqiao.cn)
问题描述
小蓝最近迷上了用火柴棒拼数字字符, 方法如下图所示:
他只能拼 0 至 9 这十种数字字符, 其中每个数字字符需要的火柴棒的数目 依次是: 6,2,5,5,4,5,6,3,7,6 。他不喜欢重复拼同一个数字字符, 所以对于每个 数字字符他最多拼十个。小蓝会把拼出来的数字字符组合在一起形成一个整数, 例如对于整数 345 , 需要的火柴棒的数目为 5+4+5=14 根。小蓝有 300 根 火柴棒, 他想知道自己能拼出的最大整数是多少? 可以不使用完这 300 根火柴 棒, 可以有多余的火柴棒剩下。
答案提交
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一 个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
【思路】
将数字看成价值为1且各有10个的物品,需要的火柴棒看成重量,这是多重背包问题。因为是填空题,没有用滚动数组优化和二进制优化。
- 为什么每个数字价值都为1?
答:因为位数越大,这个整数就越大,最大的整数肯定是位数最多的。(例如:9999<10000),每个数字都相当于给你增加了一位数, 所以每个数字价值都为1。
- 位数相同(价值相同)时,怎么选择?
数字是从小到大装进dp[ ][ ],为了拼出最大的整数,所以输出最大整数时应该按数字i从大到小考虑。当位数相同的时候就选择装了更多数字i的dp,因为装了更多数字i的dp肯定比装了较少的数字i的dp,最后拼出的整数更大。
-
定义状态dpli][j]:表示把前i个数字装进容量j的背包,能装进背包的最大价值。
【代码】
N = 300 # 背包容量
W =[0,6,2,5,5,4,5,6,3,7,6] # 每种火柴的重量
dp = [[0]*301 for i in range(11)]
for i in range(1,11): # 遍历所有数字:数字0为1,数字1为2,以此类推。for k in range(0,11): # 每个数字最多有10个,每个价值为1for j in range(k * W[i],301): # 枚举背包容量dp[i][j] = max(dp[i-1][j], dp[i - 1][j - k * W[i]] + k) # 不装或装第i个数的两种情况取最大值
j=300
for i in range(10,0,-1): # 遍历所有数字,数字9为10,数字8为9,以此类推k= 0 # 在最大价值下(dp[i][j])最多能装k个数字ifor g in range(0,11): # 遍历每种数字的数量if j-g*W[i]>=0: # 背包放得下if (dp[i][j] == dp[i - 1][j - g * W[i]] + g): # 位数(最大价值)相同时,能否装下g个数字ik = g # 记录最多能装k个j = j - k * W[i] # 背包剩余容量while k > 0: # 装了这个数字k个,就输出k个这个数字k -= 1print(i - 1, end='')
# 答案:9999999999777777777755555555554444444444333333333322222222221111题目三:22年省赛C题——近似GCD (难度:★★★)
问题描述
小蓝有一个长度为 n 的数组 A=(a1,a2,⋯,an), 数组的子数组被定义为从原数组中选出连续的一个或多个元素组成的数组。数组的最大公约数指的是数组中所有元素的最大公约数。如果最多更改数组中的一个元素之后, 数组的最大公约数为 g, 那么称 g 为这个数组的近似 GCD。一个数组的近似 GCD 可能 有多种取值。
具体的, 判断 g 是否为一个子数组的近似 GCD 如下:
如果这个子数组的最大公约数就是 g, 那么说明 g 是其近似 GCD。
在修改这个子数组中的一个元素之后 (可以改成想要的任何值), 子数组的最大公约数为 g, 那么说明 g 是这个子数组的近似 GCD。
小蓝想知道, 数组 A 有多少个长度大于等于 2 的子数组满足近似 GCD 的 值为 g 。
输入格式
输入的第一行包含两个整数 n,g, 用一个空格分隔, 分别表示数组 A 的长 度和 g 的值。
第二行包含 n 个整数 a1,a2,⋯,an, 相邻两个整数之间用一个空格分隔。
输出格式
输出一行包含一个整数表示数组 A 有多少个长度大于等于 2 的子数组的近 似 GCD 的值为 g 。
样例输入
5 3 1 3 6 4 10样例输出
5样例说明
满足条件的子数组有 5 个:
[1,3]: 将 1 修改为 3 后, 这个子数组的最大公约数为 3 , 满足条件。
[1,3,6]: 将 1 修改为 3 后, 这个子数组的最大公约数为 3 , 满足条件。
[3,6]:这个子数组的最大公约数就是 3 , 满足条件。
[3,6,4] : 将 4 修改为 3 后, 这个子数组的最大公约数为 3 , 满足条件。
[6,4] : 将 4 修改为 3 后, 这个子数组的最大公约数为 3 , 满足条件。
评测用例规模与约定
对于 20%20% 的评测用例, 2≤n≤10^2 ;
对于 40%40% 的评测用例, 2≤n≤10^3;
对于所有评测用例, 2≤n≤
1≤g,ai≤10^9 。
n最大是 ,所以最多只能用O(nlogn)的算法。
【思路】
题解
一个子数组a:
- 若a中每一项都是g的倍数,只需要将a中某个元素改为g,满足要求。
- 若a中存在一个不是g的倍数,把它改为g,满足要求。
- 若a中存在至少2个不是g的倍数,无法满足要求。
问题变成:求原数组有多少个子数组满足这个数组里最多只有一个元素不是g的倍数编码
用双指针遍历原数组 双指针复杂度:O(n)
【代码】
技巧1:用last标记当前的不满足g的倍数的点,下次a[i]再次不满足g的倍数时,j直接跳到last往后一点,确保只有一个不是g的倍数
技巧2: 每次i移动一步就记录一下双指针的距离(即满足要求的子数组个数),然后将它们累加起来,就是所有满足要求的子数组个数
n,g=map(int,input().split())
a=[0]+list(map(int,input().split()))
ans=0
last=0
j=1
for i in range(1, n+1): # 前指针往前走if a[i]%g != 0: # 不满足g的倍数j = last+1 # 后指针往前走last = i # last标记不满足点,下次a[i]再次不满足g的倍数,j直接跳到last往后一点if i-j+1 >= 2:ans += i-j # 长度大于2就开始累加
print(ans)相关文章:
蓝桥杯倒计时 | 倒计时17天
作者🕵️♂️:让机器理解语言か 专栏🎇:蓝桥杯倒计时冲刺 描述🎨:蓝桥杯冲刺阶段,一定要沉住气,一步一个脚印,胜利就在前方! 寄语💓:…...
【Spring Cloud Alibaba】7.Sentinel熔断器仪表盘监控
文章目录简介什么是 Sentinel控制台获取源码方式下载jar包方式启动访问服务配置项目,启用Sentinel完整配置测试简介 接下来我们通过Sentinel控制台来实现对服务消费者提供的熔断机制进行监控和控制,本操作先要完成之前的步骤,详情请参照【Sp…...
个人博客系统项目测试报告
项目背景介绍 背景:当在学习一项技能的时候,我们总会习惯通过博客来记录所学的知识点,方便后期遗忘时随时查看和快速复习。本次开发的Web网站程序便是为了更加轻量和方便地记录自己的学习笔记 概述:一个Web网站程序,…...

flutter安装自用笔记
参照文章: 开发环境搭建 Flutter环境配置步骤: 1.系统配置要求 2.Java环境 3.Flutter SDK 4.Android 开发环境一、系统配置要求 操作系统:Windows 7 SP1 或更高的版本(基于 x86-64 的 64 位操作系统) 磁盘空间&…...
tomcat线程池以及在SpringBoot中的启动过程
tomcat两大组件:连接器Connector,容器Container tomcat线程池 Tomcat线程池扩展了ThreadPoolExecutor,行为稍有不同 重写了ThreadPoolExecutor的execute方法 如果总线程数达到maximumPoolSize,不会立刻抛RejectedExecutionExcept…...

第十四届中国大学生创新创业大赛
文章目录比赛官网比赛题目含金量非常高建议参加的学生推荐几个我感兴趣的题目联系比赛官网 官网地址:http://www.fwwb.org.cn/ 实际叫做:中国大学生创新创业大赛 比赛题目 题目公布查看地址:http://www.fwwb.org.cn/topic/index 题目有…...

LeetCode:322. 零钱兑换——动态规划从案例入门
🍎道阻且长,行则将至。🍓 🌻算法,不如说它是一种思考方式🍀算法专栏: 👉🏻123 一、🌱322. 零钱兑换 题目描述:给你一个整数数组coins,…...
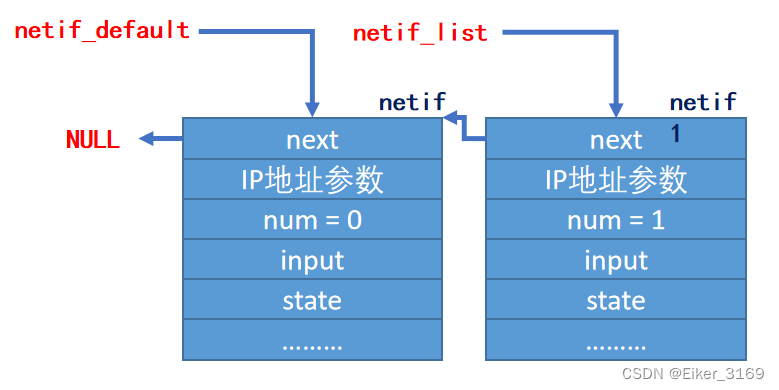
【lwIP(第四章)】网络接口
目录一、lwIP网络接口简介二、lwIP的netif结构三、lwIP的netif相关函数1. lwIP网络接口的全局变量2. netif_add()函数3. netif_remove()函数4. netif_set_default()函数一、lwIP网络接口简介 lwIP协议栈支持多种不同的网络接口(网卡),由于网卡…...

Vue3 pinia入门篇(一)
系列文章目录 主要为了记录如何使用Pinia在Vue3中的使用方式(下面会介绍为什么使用Vue3选型) 文章目录系列文章目录不用Vue2使用Pinia举例子?1.笔者的个人看法:2.总结一、Pinia是什么1.状态管理工具(类比Vuexÿ…...

python面向对象编程解释
python是一个面向对象的编程语言 面向过程的开发语言有C,面向对象除了python还有java等语言 具体来讲: 面向过程 :举个例子,比如说,把大象装进冰箱总共分几步,第一步,把冰箱门打开,…...
ARM(IMX6U)嵌入式软件裸机开发之环境搭建与配置
目录 前沿 Ubuntu 和 Windows 文件互传 Ubuntu 下 NFS 和 SSH 服务开启 Ubuntu 交叉编译工具链安装 Source Insight 软件安装和使用 Visual Studio Code 软件的安装和使用 前沿 为什么我们要学习裸机开发呢? 1、裸机开发是了解所使用的 CPU 最直接、最简单的方…...

Java文件复制多种方法
1、InputStream与OutputStream 创建两个文件 - 源和目标。然后我们从源创建InputStream并使用OutputStream将其写入目标文件进行 java 复制文件操作。 private static void copyFileUsingStream(File source, File dest) throws IOException {InputStream is null;OutputStr…...
Java语言-----封装、继承、抽象、多态、接口
目录 前言 一.封装 1.1封装的定义 1.2访问修饰符的使用 二.继承 2.1继承的定义 2.2继承的方法 2.3继承使用注意点 三.多态 3,1多态的定义 3.2动态绑定 3.3方法重写 3.4向上(向下)转型 四.抽象 4.1抽象的概述和定义 4.2抽象的使用 五…...
基于深度学习的瓶子检测软件(UI界面+YOLOv5+训练数据集)
摘要:基于深度学习的瓶子检测软件用于自动化瓶子检测与识别,对于各种场景下的塑料瓶、玻璃瓶等进行检测并计数,辅助计算机瓶子生产回收等工序。本文详细介绍深度学习的瓶子检测软件,在介绍算法原理的同时,给出Python的…...
仿网易云小程序(一)
目录 一、项目准备 二、项目初始化 1.新建项目 2.封装service请求 三、底部导航栏的设计 四、MV页面的设计 1.将获取到的数据进行渲染 2.播放量数据进行处理转换 3.时长数据进行处理转换 五、MV组件的抽离封装 六、请求的抽离video 七、下拉重新请求新的数据 八、跳转到…...
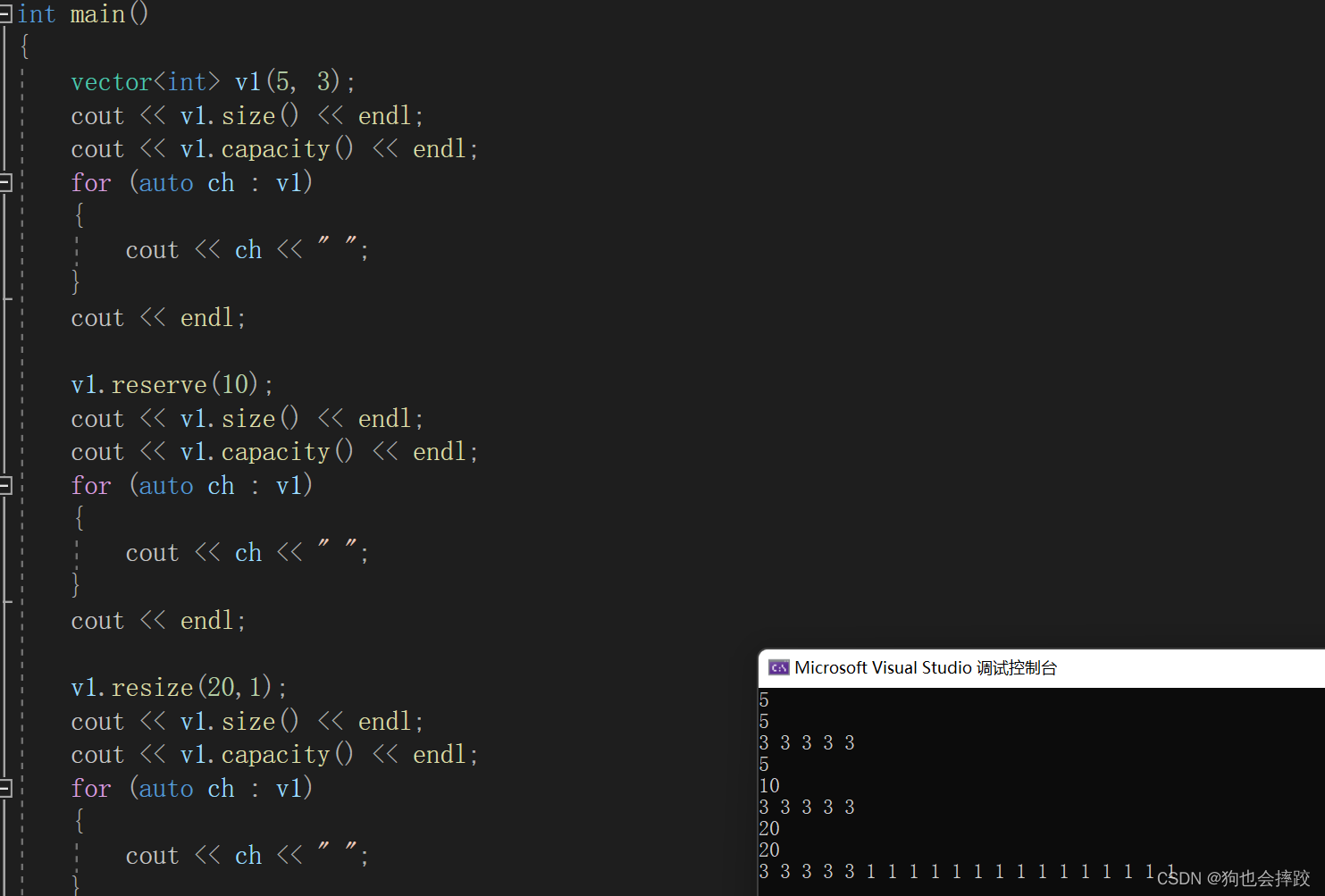
【C++】vector模拟实现及其应用
文章目录vector的介绍vector的使用及其实现vector的定义vector iterator 的使用vector空间增长问题vector的增删查改vector的介绍 vector是表示可变大小数组的序列容器。就像数组一样,vector也采用的连续存储空间来存储元素。也就是意味着可以采用下标对vector的元素…...

JS看这一篇就够啦,JS基础大全,可用于快速回顾知识,面试首选
1 JS简介 更多JS内容可以看MDN:点击传送 浏览器分成两部分:渲染引擎和 JS 引擎 渲染引擎:用来解析HTML与CSS,俗称内核,比如 chrome 浏览器的 blink ,老版本的 webkitJS 引擎:也称为 JS 解释器…...

武汉凯迪正大GB4208外壳防护等级试具
一、IP1X 试验探棒 产品概述: 符合IEC61032图1试具A、GB16842试具A、GB4208IP1、IEC60529IP1、IEC60065 等标准要求。用于防止手背触及的防护检验。 技术参数: 1、探球直径:50mm 2、挡板直径:45mm 3、挡板厚度:…...

Cent OS 从零部署ruoyi-cloud教程
1、java环境安装 https://blog.csdn.net/m0_61035257/article/details/125705400 Java_home设置 https://blog.csdn.net/m0_51104427/article/details/123924893 2、mysql安装 https://blog.csdn.net/ShockChen7/article/details/126965940 若安装的是Mysql8,建议…...

ChatGPT相关核心算法
ChatGPT 的卓越表现得益于其背后多项核心算法的支持和配合。本文将分别介绍作为其实现基础的 Transformer 模型、激发出其所蕴含知识的Prompt/Instruction Tuning 算法、其涌现出的思维链能力、以及确保其与人类意图对齐的基于人类反馈的强化学习算法。 1.基于Transformer的预…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...