数学建模笔记——TOPSIS[优劣解距离]法
数学建模笔记——TOPSIS[优劣解距离法]
- TOPSIS(优劣解距离)法
- 1. 基本概念
- 2. 模型原理
- 3. 基本步骤
- 4. 典型例题
- 4.1 矩阵正向化
- 4.2 正向矩阵标准化
- 4.3 计算得分并归一化
- 4.4 python代码实现
TOPSIS(优劣解距离)法
1. 基本概念
C. L.Hwang和 K.Yoon于1981年首次提出 TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution),可翻译为逼近理想解排序法,国内常简称为优劣解距离法。
TOPSIS法是一种常用的综合评价方法,能充分利用原始数据的信息,其结果能精确地反映各评价方案之间的差距。
TOPSIS法引入了两个基本概念:
- 理想解:设想的最优的解(方案),它的各个属性值都达到各备选方案中的最好的值;
- 负理想解:设想的最劣的解(方案),它的各个属性值都达到各备选方案中的最坏的值。方案排序的规则是把各备选方案与理想解和负理想解做比较,若其中有一个方案最接近理想解,而同时又远离负理想解,则该方案是备选方案中最好的方案。TOPSIS通过最接近理想解且最远离负理想解来确定最优选择。
2. 模型原理
TOPSIS法是一种理想目标相似性的顺序选优技术,在多目标决策分析中是一种非常有效的方法。它通过归一化后(去量纲化)的数据规范化矩阵,找出多个目标中最优目标和最劣目标(分别用理归想一解化和反理想解表示),分别计算各评价目标与理想解和反理想解的距离,获得各目标与理想解的贴近度,按理想解贴近度的大小排序,以此作为评价目标优劣的依据。贴近度取值在0~1之间,该值愈接近1,表示相应的评价目标越接近最优水平;反之,该值愈接近0,表示评价目标越接近最劣水平。
3. 基本步骤
-
将原始矩阵正向化
将原始矩阵正向化,就是要将所有的指标类型统一转化为极大型指标
-
将正向化矩阵标准化
标准化的方法有很多种,其主要目的就是去除量纲的影响,保证不同评价指标在同一数量级,且数据大小排序不
-
计算得分并归一化
S i = D i − D i + + D i − S_{i}=\frac{D_{i}^{-}}{D_{i}^{+}+D_{i}^{-}} Si=Di++Di−Di−,其中 S i S_{i} Si为得分, D i + {D_{i}^{+}} Di+为评价对象与最大值的距离, D i − D_{i}^{-} Di−
为评价对象与最小值的距离。
4. 典型例题
明星Kun想找一个对象,但喜欢他的人太多,不知道怎么选,经过层层考察,留下三个候选人。他认为身高165是最好的,体重在90-100斤是最好的。
候选人 颜值 牌气(争吵次数) 身高 体重 A 9 10 175 120 B 8 7 164 80 C 6 3 157 90
4.1 矩阵正向化
常见的指标类型:
| 指标名称 | 指标特点 | 例子 |
|---|---|---|
| 极大型 (效益型) 指标 | 越大(多)越好 | 成绩、 GDP增速、 企业利润 |
| 极小型 (成本型) 指标 | 越小(少)越好 | 费用、 坏品率、污染程度 |
| 中间型指标 | 越接近某个值越好 | 水质量评估时的PH值 |
| 区间型指标 | 落在某个区间最好 | 体温、 水中植物性营养物量 |
在 TOPSIS 方法中,就是要将所有指标进行统一正向化,即统一转化为极大型指标。 那么就需要极小型、中间型以及区间型的指标进行转化为极大型指标。
| 指标名称 | 公式 |
|---|---|
| 极大型(效益型)指标 | / |
| 极小型(成本型)指标 | x ~ = m a x − x \tilde{x} = max-x x~=max−x, x ~ \tilde{x} x~为指标值, m a x max max为指标最大值, x x x为指标值 |
| 中间型指标 | { x i } \{x_i\} {xi} 是一组中间型序列,最优值是 x b e s t x_{best} xbest,$M = max{ |
| 区间型指标 | x i {x_i} xi是一组区间型序列,最佳区间为 [ a , b ] [a,b] [a,b],正向化公式如下 M = m a x { a − m i n { x i } , m a x { x i } − b } , x ~ i = { 1 − a − x i M , x i < a 1 , a ≤ x i ≤ b 1 − x i − b M , x i > b M=max\{a-min\{x_i\}, max\{x_i\}-b\}, \widetilde{x}_i=\begin{cases}1-\frac{a-x_i}{M}, x_i<a\\1, a\leq x_i\leq b\\1-\frac{x_i-b}{M}, x_i>b\end{cases} M=max{a−min{xi},max{xi}−b},x i=⎩ ⎨ ⎧1−Ma−xi,xi<a1,a≤xi≤b1−Mxi−b,xi>b |
-
颜值为极大型指标
-
脾气为极小型指标
候选人 颜值 m a x max max m a x − x max-x max−x A 10 10 0 B 7 10 3 C 3 10 7 -
身高为中间型指标
候选人 身高 x b e s t x_{best} xbest | x i − x b e s t x_i-x_{best} xi−xbest| x ^ i \hat{x}_i x^i A 175 165 10 1 B 164 165 1 1/10 C 157 165 8 8/10 -
体重为区间型指标
候选人 体重 M M M x ^ i \hat{x}_i x^i A 120 20 0 B 80 20 1/2 C 90 20 1
正向化后的矩阵为
| 候选人 | 颜值 | 牌气(争吵次数) | 身高 | 体重 |
|---|---|---|---|---|
| A | 9 | 0 | 0 | 0 |
| B | 8 | 3 | 0.9 | 0.5 |
| C | 6 | 7 | 0.2 | 1 |
4.2 正向矩阵标准化
标准化的目的是消除不同指标量纲的影响
假设有n个要评价的对象,m个评价指标(已经正向化了)构成的正向化矩阵如下:
X = [ x 11 x 12 ⋯ x 1 m x 21 x 22 ⋯ x 2 m ⋮ ⋮ ⋱ ⋮ x n 1 x n 2 ⋯ x n m ] X=\begin{bmatrix}x_{11}&x_{12}&\cdots&x_{1m}\\x_{21}&x_{22}&\cdots&x_{2m}\\\vdots&\vdots&\ddots&\vdots\\x_{n1}&x_{n2}&\cdots&x_{nm}\end{bmatrix} X= x11x21⋮xn1x12x22⋮xn2⋯⋯⋱⋯x1mx2m⋮xnm
那么对其标准化后的矩阵记为Z,Z的每一个元素:
z i j = x i j ∑ i = 1 n x i j 2 z_{ij}=\frac{x_{ij}}{\sqrt{\sum_{i=1}^nx_{ij}^2}} zij=∑i=1nxij2xij
即(每一个元素/根号下所在列元素的平方和)得到标准化矩阵Z:
Z = [ z 11 z 12 ⋯ z 1 m z 21 z 22 ⋯ z 2 m ⋮ ⋮ ⋱ ⋮ z n 1 z n 2 ⋯ z n m ] Z=\begin{bmatrix}z_{11}&z_{12}&\cdots&z_{1m}\\z_{21}&z_{22}&\cdots&z_{2m}\\\vdots&\vdots&\ddots&\vdots\\z_{n1}&z_{n2}&\cdots&z_{nm}\end{bmatrix} Z= z11z21⋮zn1z12z22⋮zn2⋯⋯⋱⋯z1mz2m⋮znm
标准化后,还需要给不同指标加上权重,采用的权重确定方法有层次分析法、熵权法、Delphi法、对数最小二乘法。这里认为各个指标权重相同。
对上述矩阵进行标准化,得
| 候选人 | 颜值 | 牌气(争吵次数) | 身高 | 体重 |
|---|---|---|---|---|
| A | 0.669 | 0 | 0 | 0 |
| B | 0.595 | 0.394 | 0.976 | 0.447 |
| C | 0.446 | 0.919 | 0.217 | 0.894 |
4.3 计算得分并归一化
定义最大值:
Z + = ( m a x { z 11 , z 21 , ⋯ , z n 1 } , m a x { z 12 , z 22 , ⋯ , z n 2 } , ⋯ , m a x { z 1 m , z 2 m , ⋯ , z n m } ) Z^+=(max\{z_{11},z_{21},\cdots,z_{n1}\},max\{z_{12},z_{22},\cdots,z_{n2}\},\cdots,max\{z_{1m},z_{2m},\cdots,z_{nm}\}) Z+=(max{z11,z21,⋯,zn1},max{z12,z22,⋯,zn2},⋯,max{z1m,z2m,⋯,znm})
定义最小值:
Z − = ( m i n { z 11 , z 21 , ⋯ , z n 1 } , m i n { z 12 , z 22 , ⋯ , z n 2 } , ⋯ , m i n { z 1 m , z 2 m , ⋯ , z n m } ) Z^-=(min\{z_{11},z_{21},\cdots,z_{n1}\},min\{z_{12},z_{22},\cdots,z_{n2}\},\cdots,min\{z_{1m},z_{2m},\cdots,z_{nm}\}) Z−=(min{z11,z21,⋯,zn1},min{z12,z22,⋯,zn2},⋯,min{z1m,z2m,⋯,znm})
定义第i (i=1,2,…,n) 个评价对象与最大值的距离:
D i + = ∑ j = 1 m ( Z j + − z i j ) 2 D_i^+=\sqrt{\sum_{j=1}^m(Z_j^+-z_{ij})^2} Di+=j=1∑m(Zj+−zij)2
定义第i (i=1,2,…,n) 个评价对象与最小值的距离:
D i − = ∑ j = 1 m ( Z j − − z i j ) 2 D_i^-=\sqrt{\sum_{j=1}^m(Z_j^--z_{ij})^2} Di−=j=1∑m(Zj−−zij)2
那么,我们可以计算得出第 i( i=1,2,…,n) 个评价对象未归一化的得分:
S i = D i − D i + + D i − S_i=\frac{D_i^-}{D_i^++D_i^-} Si=Di++Di−Di−
很明显 0≤Si≤1,且 Si 越大 Di+ 越小,即越接近最大值。
我们可以将得分归一化并换成百分制:
S i ~ = S i ∑ i = 1 n S i × 100 \widetilde{S_{\mathrm{i}}}=\frac{S_{\mathrm{i}}}{\sum_{i=1}^{n}S_{\mathrm{i}}}\times100 Si =∑i=1nSiSi×100
4.4 python代码实现
import numpy as np# 从用户输入参评数目和指标数目
print("请输入参评数目:")
n = int(input())
print("请输入指标数目:")
m = int(input())# 接受用户输入的类型矩阵
print("请输入类型矩阵:1. 极大型 2. 极小型 3. 中间型 4.区间型")
kind = input().split(" ")# 接受用户输入的矩阵并转化为向量
print("请输入矩阵:")
A = np.zeros(shape=(n, m))
for i in range(n):A[i] = input().split(" ")A[i] = list(map(float, A[i]))
print("输入矩阵为:\n{}".format(A))# 极小型指标转化为极大型指标的函数def minTomax(maxx, x):x = list(x)ans = [[(maxx-e) for e in x]]return np.array(ans)# 中间型指标转化为极大型指标的函数def midTomax(bestx, x):x = list(x)h = [abs(e-bestx) for e in x]M = max(h)if M == 0:M = 1 # 防止最大差值为0的情况ans = [[1-(e/M) for e in h]]return np.array(ans)# 区间型指标转化为极大型指标的函数def regTomax(lowx, highx, x):x = list(x)M = max(lowx-min(x), max(x)-highx)if M == 0:M = 1 # 防止最大差值为0的情况ans = []for i in range(len(x)):if x[i] < lowx:ans.append(1-(lowx-x[i])/M)elif x[i] > highx:ans.append(1-(x[i]-highx)/M)else:ans.append(1)return np.array([ans])# 同一指标类型,将所有指标转化为极大型指标
X = np.zeros(shape=(n, 1))
for i in range(m):if kind[i] == "1":v = np.array(A[:, i])elif kind[i] == "2":maxA = max(A[:, i])v = minTomax(maxA, A[:, i])elif kind[i] == "3":print("类型三,请输入最优值:")bestA = eval(input())v = midTomax(bestA, A[:, i])elif kind[i] == "4":print("类型四,请输入区间[a,b]值a:")lowA = eval(input())print("类型四,请输入区间[a,b]值b:")highA = eval(input())v = regTomax(lowA, highA, A[:, i])if i == 0:X = v.reshape(-1, 1) # 如果是第一个指标,直接赋值else:X = np.hstack((X, v.reshape(-1, 1))) # 如果不是第一个指标,横向拼接
print("统一指标后矩阵为:\n{}".format(X))# 对统一指标后的矩阵进行标准化处理
X = X.astype(float) # 将X转化为浮点型
for i in range(m):X[:, i] = X[:, i]/np.sqrt(sum(X[:, i]**2)) # 对每一列进行归一化处理,即除以该列的欧几里得范数
print("标准化后矩阵为:\n{}".format(X))# 最大值和最小值距离的计算
x_max = np.max(X, axis=0) # 计算每一列的最大值
x_min = np.min(X, axis=0) # 计算每一列的最小值
# 计算每一个参评对象与最优情况的距离d+
d_z = np.sqrt(np.sum(np.square(X-np.tile(x_max, (n, 1))), axis=1))
# 计算每一个参评对象与最差情况的距离d-
d_f = np.sqrt(np.sum(np.square(X-np.tile(x_min, (n, 1))), axis=1))
print("每个指标的最大值为:{}".format(x_max))
print("每个指标的最小值为:{}".format(x_min))# 计算每一个参评对象的综合得分
s = d_f/(d_f+d_z) # 根据d+和d-计算每一个参评对象的得分,其中s接近1表示越好,接近0表示越差
Score = 100*s/sum(s) # 将得分转换为百分制
for i in range(n):print(f"第{i+1}个参评对象的得分为:{Score[i]}")输入:
请输入参评数目:
3
请输入指标数目:
4
请输入类型矩阵:1. 极大型 2. 极小型 3. 中间型 4.区间型
1 2 3 4
请输入矩阵:
9 10 175 120
8 7 164 80
6 3 157 90
输入矩阵为:
[[ 9. 10. 175. 120.][ 8. 7. 164. 80.][ 6. 3. 157. 90.]]
类型三,请输入最优值:
165
类型四,请输入区间[a,b]值a:
90
类型四,请输入区间[a,b]值b:
100
输出:
统一指标后矩阵为:
[[9. 0. 0. 0. ][8. 3. 0.9 0.5][6. 7. 0.2 1. ]]
标准化后矩阵为:
[[0.66896473 0. 0. 0. ][0.59463532 0.3939193 0.97618706 0.4472136 ][0.44597649 0.91914503 0.21693046 0.89442719]]
每个指标的最大值为:[0.66896473 0.91914503 0.97618706 0.89442719]
每个指标的最小值为:[0.44597649 0. 0. 0. ]
第1个参评对象的得分为:8.886366735657832
第2个参评对象的得分为:45.653341055701134
第3个参评对象的得分为:45.46029220864103
相关文章:

数学建模笔记——TOPSIS[优劣解距离]法
数学建模笔记——TOPSIS[优劣解距离法] TOPSIS(优劣解距离)法1. 基本概念2. 模型原理3. 基本步骤4. 典型例题4.1 矩阵正向化4.2 正向矩阵标准化4.3 计算得分并归一化4.4 python代码实现 TOPSIS(优劣解距离)法 1. 基本概念 C. L.Hwang和 K.Yoon于1981年首次提出 TOPSIS(Techni…...

证书学习(四)X.509数字证书整理
目录 一、X.509证书 介绍1.1 什么是 X.509证书?1.2 什么是 X.509标准?1.3 什么是 PKI?二、X.509证书 工作原理2.1 证书认证机构(CA)2.1 PKI 的基础——加密算法2.2 PKI 证书编码三、X.509证书 结构3.1 证书字段3.2 证书扩展背景: 我们在日常的开发过程中,经常会遇到各种…...

氚云,低代码领风者如何破解行业的“中式焦虑”?
To B生意“难做”,很多公司的苦恼都难以掩盖。 上半年,一个“中国软件行业全军覆没”的帖子引发热烈讨论,评论竟是赞同的居多。那些以实现上市为目标的SaaS公司,或者已经上市的、主营业务为To B的企业,其整体的业绩状…...

“深入解析:MySQL半同步复制的配置指南与实践技巧“
本次配置是在已搭建好主从复制的架构中进行配置 配置环境 操作系统 master节点 slave节点 centos7 8.0.37 8.0.37 配置半同步复制 配置master 安装master半同步复制插件 INSTALL PLUGIN rpl_semi_sync_source SONAME semisync_source.so; 在MySQL的配置文件中添加配置…...

第四届长城杯部分wp
还是太菜了,要经常练了 1.BrickGame 读源码可以看到时间的值是由js设定的,所以控制台将timeleft的时间改成999999 通过游戏就可以得到flag 2.SQLUP 一道文件上传的题目,在登陆页面我用admin和1登陆成功了,但是按照正常的应该是…...
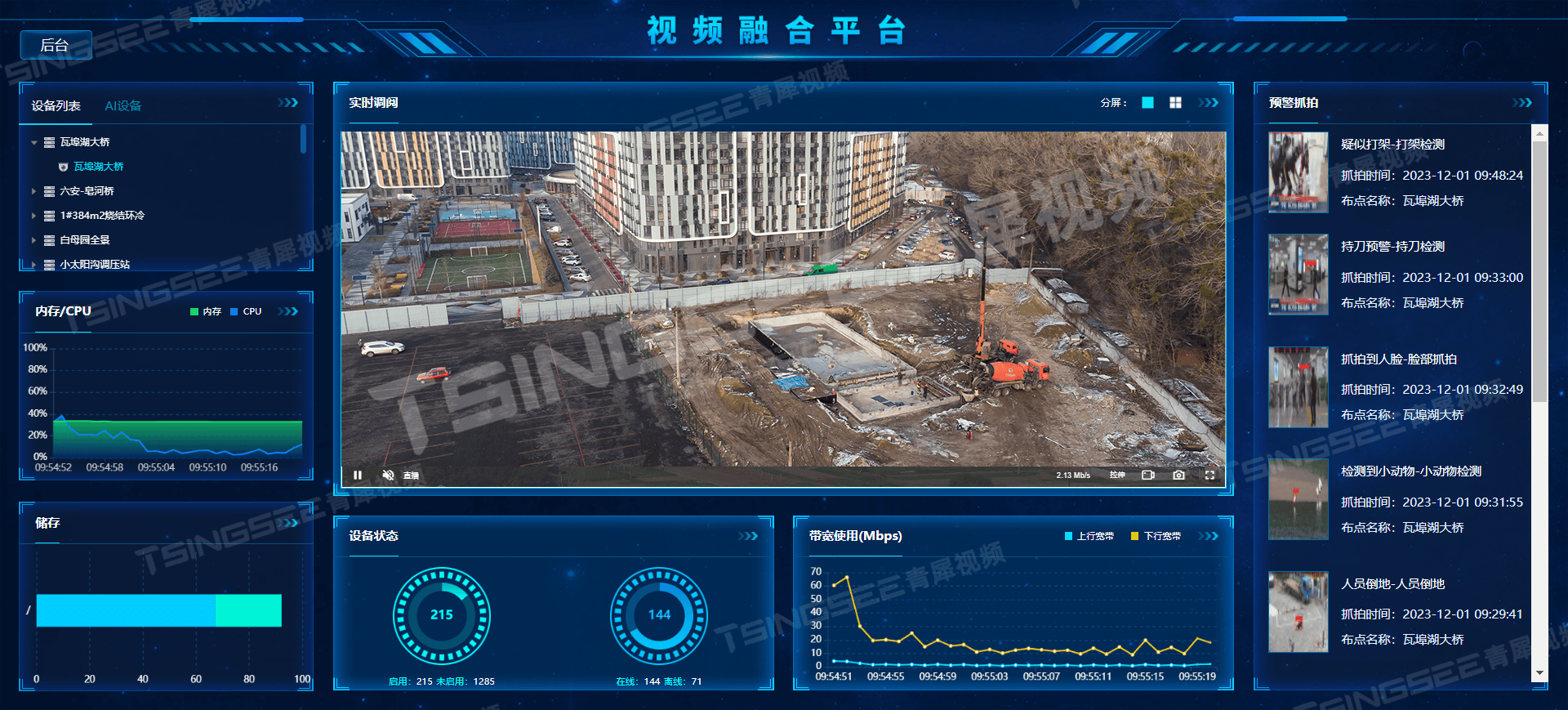
打造无死角安防网:EasyCVR平台如何助力智慧警务实现视频+AI的全面覆盖
一、背景概述 随着科技的飞速发展,智慧城市建设已成为提升社会治理能力、增强公共安全水平的重要途径。在警务领域,智慧警务作为智慧城市的重要组成部分,正通过融合视频监控技术与人工智能(AI)解决方案,实…...

批发订货系统源码怎么弄 门店订货系统小程序价格
上线批发订货系统可以显著提升业务效率和管理水平,它能够帮助企业自动化处理订单、实时跟踪库存、简化订单管理、生成数据报表…这些优势能最终帮助你降低成本、提高效率,提升业务竞争力。今天,小编为您分享批发订货系统源码怎么弄。大家点赞…...

终端安全如何防护?一文为你揭晓答案!
终端安全防护是确保组织内部网络及其连接设备免受威胁的关键措施。 以下是终端安全防护的一些核心方法: 1. 资产管理与识别 摸清家底:识别所有连接到网络的终端设备及其状态,包括硬件和软件配置。 资产分类:确定哪些资产最为关…...
价值流架构指南:构建业务创新与竞争优势的全面方法论
如何通过价值流引领企业数字化转型? 在当前数字化转型的背景下,企业面临的挑战日益复杂化:如何更快响应市场变化?如何优化资源配置提升效率?如何确保客户体验始终处于行业领先?《价值流指南》由The Open G…...

知识蒸馏(Knowledge Distillation)
Distilling the Knowledge in a Neural Network 知识蒸馏原理 1、Summarize 知识蒸馏技术 通过从大型的教师模型向小型的学生模型转移知识来实现模型压缩和优化。 知识蒸馏的核心思想是 利用教师模型在大量数据上积累的丰富知识,通过特定的蒸馏算法,使…...

【zsh】Linux离线安装zsh
首先从GitHub下载源码,然后编译源码后安装。以下是具体的步骤: 1. 下载并解压源码 首先,从GitHub下载了zsh源码的压缩包并解压到某个目录: tar -xvf zsh-<version>.tar.gz cd zsh-<version>2. 安装编译所需的依赖&…...
一款好用的电子样本册转换器
在数字化时代,电子样本册已成为各行各业必备的工具。一款好用的电子样本册转换器,可以让你在繁杂的资料管理中轻松解脱。今天,就为大家推荐一款实用的电子样本册转换神器,让你的工作效率翻倍! 工具推荐:FLB…...
TDesign:腾讯的开源企业级前端框架,能和ant-design一战吗?
TDesign 是一套拥有完整的 设计价值观 和 视觉风格指南 的企业级设计体系,同时提供了丰富的 设计资源。TDesign 在设计体系基础上产出基于 Vue、React、小程序等业界主流技术栈的组件库解决方案。是不是有点晚了? 请大家各抒己见。...

大语言模型LLM权重4bit向量量化(Vector Quantization)/查找表量化基本原理
参考 https://apple.github.io/coremltools/docs-guides/source/opt-palettization-overview.html https://apple.github.io/coremltools/docs-guides/source/opt-palettization-algos.html Apple Intelligence Foundation Language Models 苹果向量量化: DKM:…...

学习threejs,创建立方体,并执行旋转动画
文章目录 一、前言二、代码示例三、总结 一、前言 本文基于threejs,实现立方体的创建,并加入立方体旋转动画 二、代码示例 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>l…...

2024网安周今日开幕,亚信安全亮相30城
2024年国家网络安全宣传周今天在广州拉开帷幕。今年网安周继续以“网络安全为人民,网络安全靠人民”为主题。2024年国家网络安全宣传周涵盖了1场开幕式、1场高峰论坛、5个重要活动、15场分论坛/座谈会/闭门会、6个主题日活动和网络安全“六进”活动。亚信安全出席20…...

Unity Qframework 加载UI的方式
如图所示 : // Resources 加载 UIKit.OpenPanel("Resources/UIPrefab/UIMenuPanel"); // Resources 加载并传递数据 UIKit.OpenPanel<UIMenuPanel>(new UIMenuPanelData() { m_Modle this.m_Modle }, prefabName: "UIPrefab/UIMenuPanel"); …...

使用 Python 创建自动抽奖程序
介绍 自动抽奖程序在各种场景中非常有用,比如社交媒体活动、公司抽奖、在线课程奖励等。在这篇博文中,我们将学习如何使用 Python 创建一个自动抽奖程序。我们将涵盖以下内容: 需求分析环境设置基本抽奖逻辑图形用户界面(GUI&am…...

推荐10款功能强大的电脑监控软
随着工作环境和信息安全要求的不断提高,越来越多的企业和个人开始关注电脑监控软件。电脑监控软件能够帮助管理者监控员工工作效率、保护敏感信息、防止数据泄露等。下面,我们将为大家推荐10款功能强大的电脑监控软件,涵盖国内外的知名产品&a…...

‘“node“‘ �����ڲ����ⲿ���Ҳ���ǿ����еij��� ���������ļ���
错误信息 使用vscode提交前端代码到git时,报下面的错,一直不知道啥原因,后来找到了个临时解决方案。。。 vscode解决方案 package.json文件中,去掉hooks的配置。 Idea解决方案 网上有说idea的解决方案的:就是提…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
