如何在 Kali Linux 上安装 pip3
如何在 Kali Linux 上安装 pip3
在 Kali Linux 上安装 pip3 的过程非常简单。按照以下步骤,你可以轻松完成安装并开始使用 pip3 管理 Python 软件包。
步骤 1:打开终端
首先,打开你的 Kali Linux 终端。
步骤 2:更新软件包列表
为了确保你的软件包列表是最新的,运行以下命令:
sudo apt update
步骤 3:安装 pip3
接下来,安装 pip3 工具及其依赖项。运行以下命令:
sudo apt install python3-pip
安装完成后,你可以通过以下命令验证 pip3 是否成功安装:
pip3 --version
如果一切顺利,你将看到 pip3 的版本信息,这意味着 pip3 已经成功安装。
安装 pip2(可选)
如果你还需要安装 pip2(适用于 Python 2),可以按照以下步骤进行:
-
下载
get-pip.py脚本:curl https://bootstrap.pypa.io/pip/2.7/get-pip.py -o get-pip.py -
使用 Python 2 执行脚本以安装 pip2:
sudo python2 get-pip.py -
验证 pip2 是否成功安装:
pip2 -V
通过这些步骤,你可以在 Kali Linux 上安装并验证 pip3 和 pip2。现在,你可以使用 pip3 管理 Python 3 的软件包和依赖项,或者使用 pip2 来处理 Python 2 的需求。
希望这些信息对你有帮助!如果你有任何问题或需要进一步的帮助,请随时在评论区留言。
相关文章:

如何在 Kali Linux 上安装 pip3
如何在 Kali Linux 上安装 pip3 在 Kali Linux 上安装 pip3 的过程非常简单。按照以下步骤,你可以轻松完成安装并开始使用 pip3 管理 Python 软件包。 步骤 1:打开终端 首先,打开你的 Kali Linux 终端。 步骤 2:更新软件包列表…...

5.2 排列与代数余子式
一、求行列式的方法 计算机是利用主元计算行列式的。本节介绍其它两种计算行列式的方法。一是 “大公式”(big formula),它使用了全部 n ! n! n! 个排列计算;二是 “代数余子式公式”(cofactor formula)&…...

java框架第五课(终极版本)SpringBoot
一.关于SpringBoot (1)回忆Spring 传统的Spring由Spring 框架(ioc,aop)加mybatis加Springweb组成,虽然相比原生的java程序Spring框架帮我们大大减少了代码量,减少了冗余,提高了开发效率但是由于Spring框架下的配置和相关的jar包依赖过多&am…...

聚类案例——汽车是否值得购买
对汽车是否值得购买,进行聚类分析: 1、数据指标解释: buying, 购买费用 maint, 维修费用 doors, 车门数量 person, 乘坐人数 lug_boot, 行李箱容量 safety, 安全性 2、对数据进行转换 将字符串转换映射量化为数字 数据加载:…...

网络编程9.10
使用数据库完成工人管理系统: ubuntuubuntu:DB$ ubuntuubuntu:DB$ cat 2.c #include <myhead.h> #include <sqlite3.h> #include <string.h>typedef struct {int id;char name[20];double salary; } Worker;int do_insert(sqlite3 *ppDb) {Worker work;pri…...
如何在SQL Server中恢复多个数据库?
一次性恢复多个 SQL数据库吗可以吗? "是的,可以一次性恢复多个 SQL 数据库。通常情况下,只要备份文件的名称与相应的数据库匹配,且没有附加的日期或时间信息,就可以通过有效的 T-SQL 脚本来完成恢复。如果你希望…...
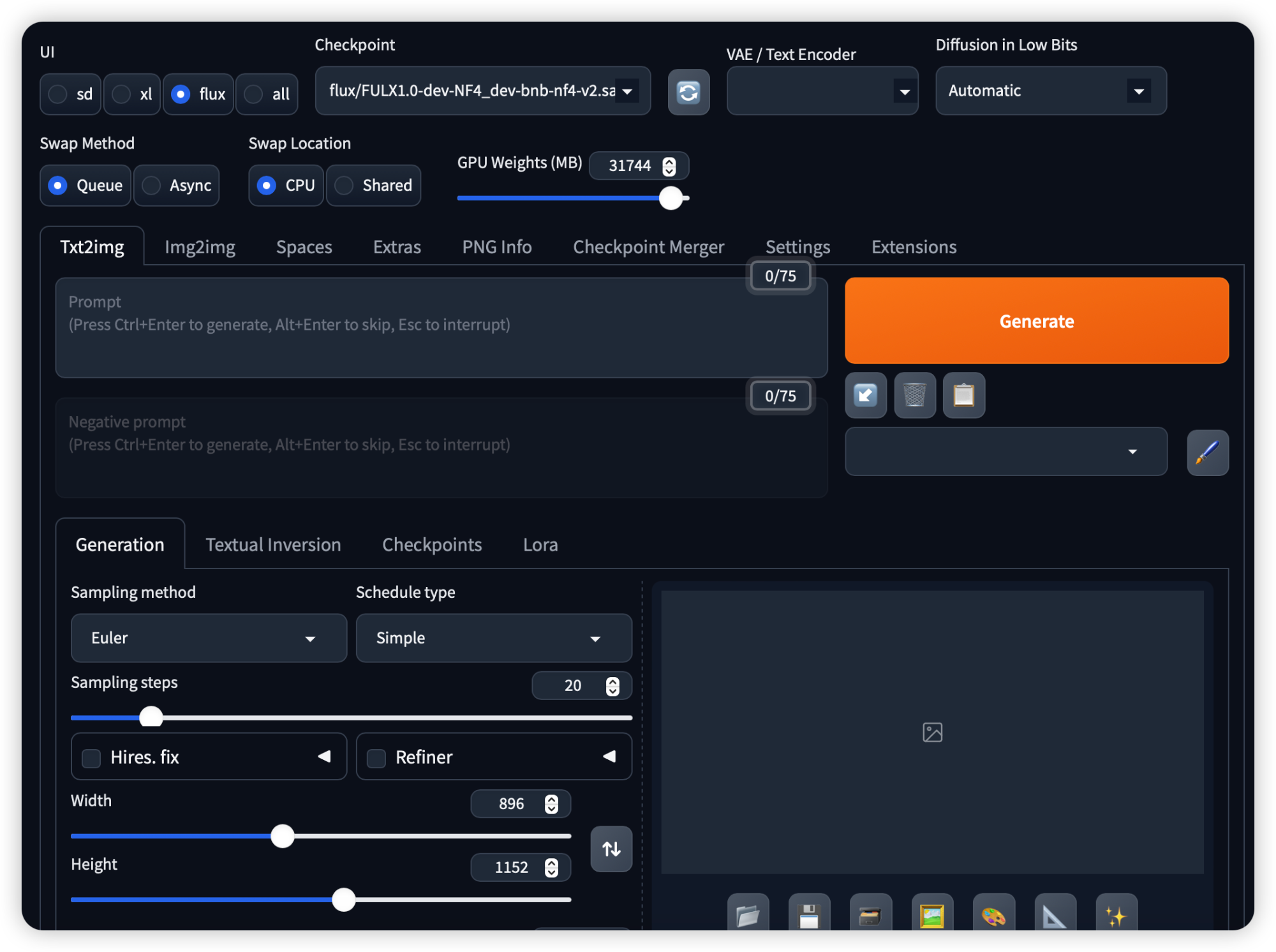
炸裂!新版 SD WebUI Forge 出图速度更快!支持最新Flux 模型!(保姆级安装教程)
大家是不是经常为SD WebUI卡顿、爆显存而苦恼?一启动SD 电脑就开始发烫, 尤其低显存用户屡屡"中招",不得不一遍遍重启。作为AI绘画的必备工具,WebUI却还有这么多"坑",着实让人不爽!😠 好消息是,…...

laserOdometry.cpp源码注释
本博客用于a-loam源码学习,用于和slam初学者一起学习。 #include <cmath>#include <nav_msgs/Odometry.h>#include <nav_msgs/Path.h> //这两行代码是C中包含头文件的指令,它们用于在ROS(Robot Operating System…...

STM32时钟配置图详解
一图概述: 左侧输入时钟源 Input Frequency (LSE/LSI/HSI/HSE) LSE (Low-Speed External):外部32.768 kHz晶体振荡器,通常用于RTC(实时时钟)。LSI (Low-Speed Internal):内部低速时钟,频率为…...

Vscode——调试时,修改变量值
第一步:点击变量,鼠标右键 第二步:点击 设置值...
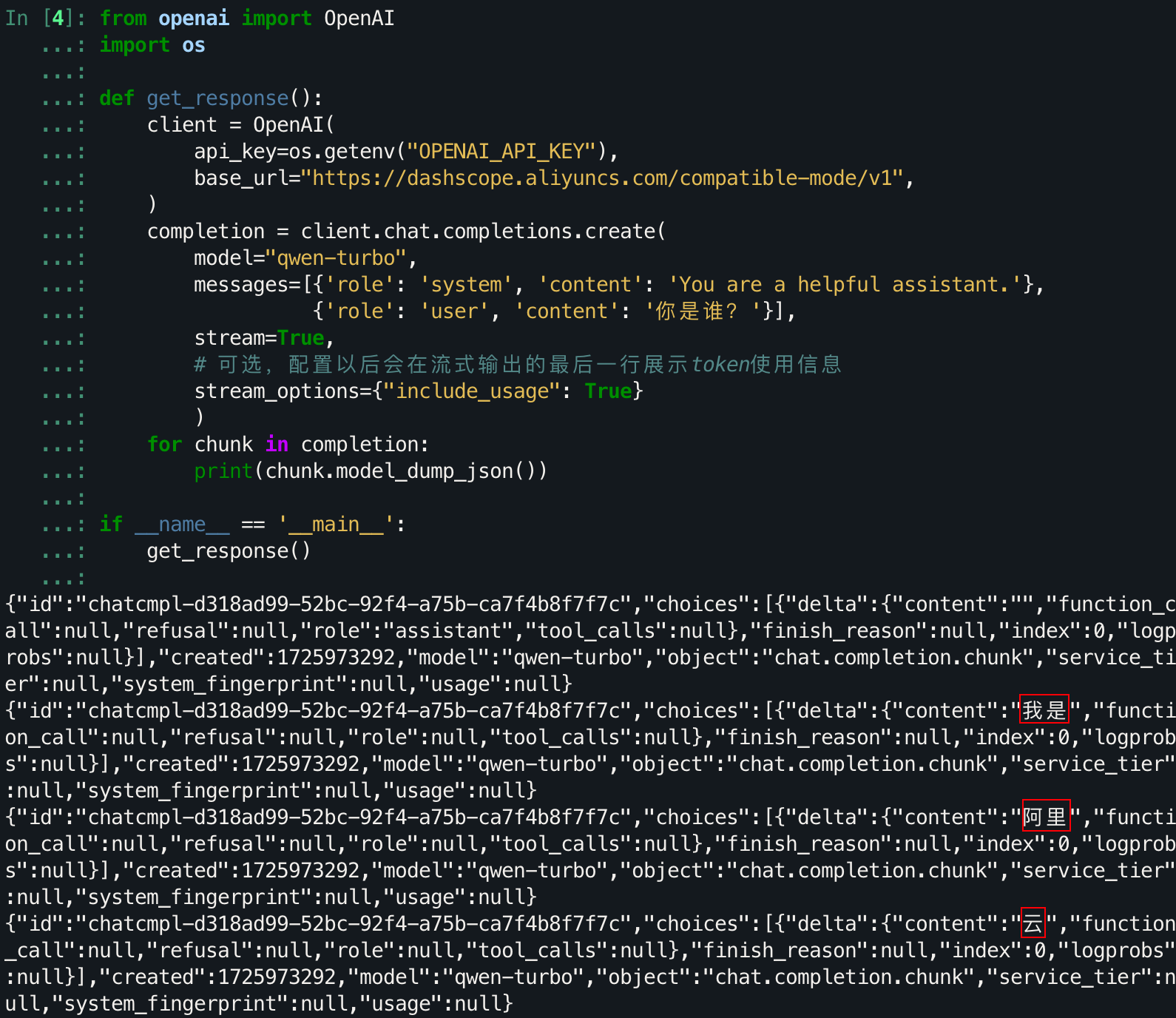
1. 初识LLM API:环境配置与多轮对话演示
其实AI应用并不是一个什么很高大上的东西,你可以将它当作一个文字的“调库”行为,“调库”只需要知道库名就行了,这里实际也是如此。甚至你只需要知道你想问什么,将你的消息作为输入,就能从大模型得到输出。而这个“库…...

【AI编程助手】VsCode插件--通义灵码
目录 摘要 一、插件安装 二、“通义灵码” 使用 三、官网教程 四、总结 五、参考信息 摘要 通义灵码是一款强大的 AI 编程助手。它能够理解编程相关的复杂逻辑,为开发者提供高效、准确的代码生成与优化建议。在编程过程中,它可以辅助处理各种任务&…...

9月10号的学习
//界面1 头文件 signals://界面1的自定义信号void my_signal(); private slots:void on_pushButton_2_clicked();void on_pushButton_clicked(); //界面1 .cpp文件 void Widget::on_pushButton_2_clicked() {QMessageBox msg(QMessageBox::Warning,"警告","是否…...

QtC++截图支持窗口获取
介绍 在截图工具中你会发现,接触到窗口后会自动圈出目标窗口,个别强大一点的还能进行元素识别可以自动圈出元素,那么今天简单分析一下QTc如何获取窗口并圈出当前鼠标下的窗口。 介绍1.如何获取所有窗口2.比较函数3.实现窗口判断 结尾 1.如何获取所有窗口…...

料品档案没有配置主供应商信息
这个问题经常会出现在普通用户的面前。没有合适的工程人员去打理料品档案。信息是缺漏的。用友给出来的提示,也让人摸不着头脑。只能是记下来备用吧。...

springboot属性加载优先级和常见命令行属性
属性加载优先级: 1.SpringApplication:启动的main方法里注入的属性 2.PropertySource:通过注解 加载的数据配置文件 3.Config data file:application.yml/.properties 4.OS environment variable:环境变量 5.Command l…...

Math Reference Notes: 因式定理
文章目录 1. 因式定理的定义2. 因式定理的数学表达:3. 因式定理的推导4. 因式定理的含义5. 因式定理的应用6. 因式定理与余式定理的关系7. 因式定理的应用领域8.因式定理的局限性 因式定理是多项式代数中的一个重要工具,帮助我们通过多项式的根来因式分解…...

Kubernetes------Service
目录 一、属性说明 二、定义和基本配置 1、定义 2、创建Service 2.1、typeClusterIP 2.2、typeNodePort 2.3、固定IP访问 三、Service、EndPoint、Pod之间的关系 四、服务发现 1、基于Service中IP访问外部服务 2、基于Service中域名访问外部服务 五、Ingress的安装和使…...

C#的LINQ语句
在 C# 中,LINQ(Language Integrated Query)是一种强大的查询技术,它允许你使用熟悉的 C# 语法来查询数据集合。LINQ 可以用于查询各种数据源,包括数组、列表、数据集、SQL数据库等。 以下是一些基本的 LINQ 语句示例&…...

项目实战系列三: 家居购项目 第三部分
文章目录 🍃后台分页🍅后台分页导航 🍃首页分页🍅首页分页导航🍅首页搜索🍅两个奇怪的问题🍅会员显示登录名🍅注销登录🍅验证码 🍃后台分页 程序框架图 1.…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

拟合问题处理
在机器学习中,核心任务通常围绕模型训练和性能提升展开,但你提到的 “优化训练数据解决过拟合” 和 “提升泛化性能解决欠拟合” 需要结合更准确的概念进行梳理。以下是对机器学习核心任务的系统复习和修正: 一、机器学习的核心任务框架 机…...

Appium下载安装配置保姆教程(图文详解)
目录 一、Appium软件介绍 1.特点 2.工作原理 3.应用场景 二、环境准备 安装 Node.js 安装 Appium 安装 JDK 安装 Android SDK 安装Python及依赖包 三、安装教程 1.Node.js安装 1.1.下载Node 1.2.安装程序 1.3.配置npm仓储和缓存 1.4. 配置环境 1.5.测试Node.j…...

无需布线的革命:电力载波技术赋能楼宇自控系统-亚川科技
无需布线的革命:电力载波技术赋能楼宇自控系统 在楼宇自动化领域,传统控制系统依赖复杂的专用通信线路,不仅施工成本高昂,后期维护和扩展也极为不便。电力载波技术(PLC)的突破性应用,彻底改变了…...
