数学建模笔记—— 灰色关联分析[GRA]
数学建模笔记—— 灰色关联分析[GRA]
- 灰色关联分析(GRA)
- 1. 相关概念
- 1.1 灰色系统
- 1.2 什么是关联分析?
- 1.3 灰色关联分析
- 2. 关联分析步骤
- 3. 典型例题
- 3.1 关联分析例题
- 3.2 灰色关联综合评价
- 4. python代码实现
- 4.1 关联分析
- 4.2 灰色关联综合评价
灰色关联分析(GRA)
1. 相关概念
1.1 灰色系统
灰色系统理论是1982年由邓聚龙创立的一门边缘性学科(interdisciplinary)。灰色系统用颜色深浅反映信息量的多少。说一个系统是黑色的,就是说这个系统是黑洞洞的,信息量太少;说一个系统是白色的,就是说这个系统是清楚的,信息量充足。而处于黑白之间的系统,或说信息不完全的系统,称为灰色系统或简称灰系统。
“信息不完全”是灰的基本含义,一般指:
- 系统因素不完全明确
- 因素关系不完全清楚
- 系统的结构不完全知道
- 系统的作用原理不完全明了
| 白 | 黑 | 灰 | |
|---|---|---|---|
| 从表象看 | 明朗 | 暗 | 若明若暗 |
| 从过程看 | 新 | 旧 | 新旧交替 |
| 从性质看 | 纯 | 不纯 | 多种成分 |
| 从信息看 | 完全 | 不完全 | 部分完全 |
| 从结果看 | 唯一的解 | 无数的解 | 非唯一性 |
| 从态度看 | 肯定 | 否定 | 扬弃 |
| 从方法看 | 严厉 | 放纵 | 宽容 |
1.2 什么是关联分析?
所谓关联分析,就是系统地分析因素。回答的问题是:某个包含多种因素的系统中,哪些因素是主要的,哪些是次要的;哪些因素影响大,哪些因素影响小;哪些因素是明显,哪些因素是潜在的。哪些是需要发展的;哪些需要抑制。
现有因素分析的量化方法,大都是数理统计法如回归分析、方差分析、主要成分分析等,这些方法都有下述弱点:
- 要求大量数据,数据量少难以找到统计规律
- 要求分布是典型的(线性的、指数的或对数的),即使是典型的并非都能处理
- 计算工作量大,一般需要计算机帮助
- 有时可能出现反常情况,如正相关则断为负相关,以至正确现象受到歪曲和颠倒
1.3 灰色关联分析
灰色关联度分析(Grey Relation Analysis、GRA),是一种多因素统计分析的方法。灰色关联分析方法弥补了采用数理统计方法作系统分析所导致的缺憾。它对样本量的多少和样本有无规律都同样适用,而且计算量小,十分方便,更不会出现量化结果与定性分析结果不符的情况。
灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密。曲线越接近,相应序列之间的关联度就越大,反之就越小。
对一个抽象的系统或现象进行分析,首先要选准反映系统行为特征的数据序列,称为找系统行为的映射量,用映射量来间接地表征系统行为。例如,用国民平均接受教育的年数来反映教育发达程度,用刑事案件的发案率来反映社会治安面貌和社会秩序,用医院挂号次数来反映国民的健康水平等。有了系统行为特征数据和相关因素的数据,即可作出各个序列的图形,从直观上进行分析。
2. 关联分析步骤
-
指标正向化
所谓正向化处理,就是将极小型、中间型以及区间型指标统一转化为极大型指标。
-
确定分析数列
-
母序列(又称参考数列,母指标):能反映系统应为特征的数据序列,其类似于因变量 Y Y Y,记为 Y = [ y 1 , y 2 , ⋯ , y n ] T Y=\left[y_{1},y_{2},\cdots,y_{n}\right]^{T} Y=[y1,y2,⋯,yn]T
-
子序列(又称比较数列,子指标):影响系统行为的因素组成的数据序列,其类似于自变量 X X X,记为
X n m = [ x 11 x 12 ⋯ x 1 m x 21 x 22 ⋯ x 2 m ⋮ ⋮ ⋱ ⋮ x n 1 x n 2 ⋯ x n m ] X_{nm}=\begin{bmatrix}x_{11}&x_{12}&\cdots&x_{1m}\\x_{21}&x_{22}&\cdots&x_{2m}\\\vdots&\vdots&\ddots&\vdots\\x_{n1}&x_{n2}&\cdots&x_{nm}\end{bmatrix} Xnm=⎣⎢⎢⎢⎡x11x21⋮xn1x12x22⋮xn2⋯⋯⋱⋯x1mx2m⋮xnm⎦⎥⎥⎥⎤
-
-
数据预处理
由于不同要素具有不同量纲和数据范围,因此我们要对他们进行预处理去量纲,将他们统一到近似的范围内,先求出每个指标的均值,在用指标中的元素除以其均值
y k ~ = y k y i , y i ‾ = 1 n ∑ k = 1 n y k x k i ~ = x k i x i , x i ‾ = 1 n ∑ k = 1 n x k i ( i = 1 , 2 , ⋯ , m ) \widetilde{y_{k}}=\frac{y_{k}}{y_{i}},\overline{y_{i}}=\frac{1}{n}\sum_{k=1}^{n}y_{k}\quad\widetilde{x_{ki}}=\frac{x_{ki}}{x_{i}},\overline{x_{i}}=\frac{1}{n}\sum_{k=1}^{n}x_{ki}\left(i=1,2,\cdots,m\right) yk =yiyk,yi=n1k=1∑nykxki =xixki,xi=n1k=1∑nxki(i=1,2,⋯,m) -
计算灰色关联系数
计算子序列中各个指标与母序列的关联系数
记 为 : a = min i min k ∣ x 0 ( k ) − x i ( k ) ∣ a=\min_{i}\min_{k}\left | x_{0}\left ( k\right ) - x_{i}\left ( k\right ) \right | a=minimink∣x0(k)−xi(k)∣, b = max i m a x k ∣ x 0 ( k ) − x i ( k ) ∣ b= \max _{i}max_k\left | x_{0}\left ( k\right ) - x_{i}\left ( k\right ) \right | b=maximaxk∣x0(k)−xi(k)∣
为两极最小差和最大差
构造: ξ i ( k ) = y ( x 0 ( k ) , x i ( k ) ) = a + ρ b ∣ x 0 ( k ) − x i ( k ) ∣ + ρ b \xi _i( k) = y\left ( x_{0}\left ( k\right ) , x_{i}\left ( k\right ) \right ) = \frac {a+ \rho b}{\left | x_{0}\left ( k\right ) - x_{i}\left ( k\right ) \right | + \rho b} ξi(k)=y(x0(k),xi(k))=∣x0(k)−xi(k)∣+ρba+ρb 其中 ρ \rho ρ为分辨系数,一般取0.5
-
计算关联度
r i = 1 n ∑ k = 1 n ξ i ( k ) = 1 n ∑ k = 1 n y ( x 0 ( k ) , x i ( k ) ) r_{i}=\frac{1}{n}\sum_{k=1}^{n}\xi_{i}\left(k\right)=\frac{1}{n}\sum_{k=1}^{n}y\Big(x_{0}\left(k\right),x_{i}\left(k\right)\Big) ri=n1k=1∑nξi(k)=n1k=1∑ny(x0(k),xi(k))
3. 典型例题
3.1 关联分析例题
已知某地国民生产总值,工业和农业生产总值,原始数据的形式及来源见下表,分析工业农业哪个对国民生产总值影响大
项目名称 年份 2016 2017 2018 2019 国民生产总值 55 65 75 100 工业产值 24 38 40 50 农业产值 10 22 18 20
-
定义母序列及子序列如下
项目名称 年份 项目代号 2016 2017 2018 2019 国民生产总值 55 65 75 100 X0(母序列) 工业产值 24 38 40 50 X1(子序列) 农业产值 10 22 18 20 X2(子序列) -
数据预处理
对数据进行均值化 y k ~ = y k y i , y i ‾ = 1 n ∑ k = 1 n y k x k i ~ = x k i x i , x i ‾ = 1 n ∑ k = 1 n x k i ( i = 1 , 2 , ⋯ , m ) \widetilde{y_{k}}=\frac{y_{k}}{y_{i}},\overline{y_{i}}=\frac{1}{n}\sum_{k=1}^{n}y_{k}\quad\widetilde{x_{ki}}=\frac{x_{ki}}{x_{i}},\overline{x_{i}}=\frac{1}{n}\sum_{k=1}^{n}x_{ki}\left(i=1,2,\cdots,m\right) yk =yiyk,yi=n1∑k=1nykxki =xixki,xi=n1∑k=1nxki(i=1,2,⋯,m)
项目名称 年份 项目代号 2016 2017 2018 2019 国民生产总值 0.75 0.88 1.02 1.36 (母序列) 工业产值 0.63 1.00 1.05 1.32 (子序列) 农业产值 0.57 1.26 1.03 1.14 (子序列) -
求关联系数
a = min i min k ∣ x 0 ( k ) − x i ( k ) ∣ b = max i m a x k ∣ x 0 ( k ) − x i ( k ) ∣ ξ i ( k ) = y ( x 0 ( k ) , x i ( k ) ) = a + ρ b ∣ x 0 ( k ) − x i ( k ) ∣ + ρ b a= \min _{i}\min _{k}\left | x_{0}\left ( k\right ) - x_{i}\left ( k\right ) \right |\\ b= \max _{i}max_k\left | x_{0}\left ( k\right ) - x_{i}\left ( k\right ) \right |\\ \xi _i( k) = y\left ( x_{0}\left ( k\right ) , x_{i}\left ( k\right ) \right ) = \frac {a+ \rho b}{\left | x_{0}\left ( k\right ) - x_{i}\left ( k\right ) \right | + \rho b} a=iminkmin∣x0(k)−xi(k)∣b=imaxmaxk∣x0(k)−xi(k)∣ξi(k)=y(x0(k),xi(k))=∣x0(k)−xi(k)∣+ρba+ρbk X_0 X_1 X_2 |x_0(k)-x_1(k)| |x_0(k)-x_2(k)| 1 0.75 0.63 0.57 0.12 0.18 2 0.88 1.00 1.26 0.12 0.38 3 1.02 1.05 1.03 0.03 0.01 4 1.36 1.32 1.14 0.04 0.22 得a=0.01,b=0.38
ξ i ( k ) = y ( x 0 ( k ) , x i ( k ) ) = 0.01 + 0.5 × 0.38 ∣ x 0 ( k ) − x i ( k ) ∣ + 0.5 × 0.38 = 0.2 ∣ x 0 ( k ) − x i ( k ) ∣ + 0.19 \begin{aligned} \xi_{i}\left(k\right)=y\left(x_{0}\left(k\right),x_{i}\left(k\right)\right)& =\frac{0.01+0.5\times0.38}{\left|x_{0}\left(k\right)-x_{i}\left(k\right)\right|+0.5\times0.38} \\ &=\frac{0.2}{\left|x_{0}\left(k\right)-x_{i}\left(k\right)\right|+0.19} \end{aligned} ξi(k)=y(x0(k),xi(k))=∣x0(k)−xi(k)∣+0.5×0.380.01+0.5×0.38=∣x0(k)−xi(k)∣+0.190.2k ∥ x 0 ( k ) − x 1 ( k ) ∥ \|x_{0}(k)-x_{1}(k)\| ∥x0(k)−x1(k)∥ ∥ x 0 ( k ) − x 2 ( k ) ∥ \|x_{0}(k)-x_{2}(k)\| ∥x0(k)−x2(k)∥ ξ 1 \xi_1 ξ1 ξ 2 \xi_2 ξ2 1 0.12 0.18 0.645 0.541 2 0.12 0.38 0.645 0.351 3 0.03 0.01 0.909 1.000 4 0.04 0.22 0.870 0.488 -
求关联度
r i = 1 n ∑ k = 1 n ξ i ( k ) = 1 n ∑ k = 1 n y ( x 0 ( k ) , x i ( k ) ) r_{i}=\frac{1}{n}\sum_{k=1}^{n}\xi_{i}\left(k\right)=\frac{1}{n}\sum_{k=1}^{n}y\Big(x_{0}\left(k\right),x_{i}\left(k\right)\Big) ri=n1k=1∑nξi(k)=n1k=1∑ny(x0(k),xi(k))k ξ 1 \xi_1 ξ1 ξ 2 \xi_2 ξ2 1 0.645 0.541 2 0.645 0.351 3 0.909 1.000 4 0.870 0.488 r r r 0.767 0.595 由 r 1 > r 2 r_1>r_2 r1>r2,工业产值关联度更大。
3.2 灰色关联综合评价
换个方法给明星Kun找一个对象,经过层层考察,留下三个候选人。他认为身高165是最好的,体重在90-100斤是最好的。
候选人 颜值 牌气(争吵次数) 身高 体重 A 9 10 175 120 B 8 7 164 80 C 6 3 157 90
-
数据正向化
将原始矩阵正向化,就是要将所有的指标类型统一转化为极大型指标。
X n m = [ x 11 x 12 ⋯ x 1 m x 21 x 22 ⋯ x 2 m ⋮ ⋮ ⋱ ⋮ x n 1 x n 2 ⋯ x n m ] X_{nm}=\begin{bmatrix}x_{11}&x_{12}&\cdots&x_{1m}\\x_{21}&x_{22}&\cdots&x_{2m}\\\vdots&\vdots&\ddots&\vdots\\x_{n1}&x_{n2}&\cdots&x_{nm}\end{bmatrix} Xnm=⎣⎢⎢⎢⎡x11x21⋮xn1x12x22⋮xn2⋯⋯⋱⋯x1mx2m⋮xnm⎦⎥⎥⎥⎤候选人 颜值 牌气(争吵次数) 身高 体重 A 9 0 0 0 B 8 3 0.9 0.5 C 6 7 0.2 1 -
正向化后的数据进行预处理
每个指标的元素除以该指标元素的平均值。
Z n m = [ z 11 z 12 ⋯ z 1 m z 21 z 22 ⋯ z 2 m ⋮ ⋮ ⋱ ⋮ z n 1 z n 2 ⋯ z n m ] Z_{nm}=\begin{bmatrix}z_{11}&z_{12}&\cdots&z_{1m}\\z_{21}&z_{22}&\cdots&z_{2m}\\\vdots&\vdots&\ddots&\vdots\\z_{n1}&z_{n2}&\cdots&z_{nm}\end{bmatrix} Znm=⎣⎢⎢⎢⎡z11z21⋮zn1z12z22⋮zn2⋯⋯⋱⋯z1mz2m⋮znm⎦⎥⎥⎥⎤候选人 颜值 牌气(争吵次数) 身高 体重 A 1.17 0.00 0.00 0.00 B 1.04 0.90 2.45 1.00 C 0.78 2.10 0.55 2.00 -
构造母序列
选取每个指标的最大值作为母序列
Y = [ y 1 , y 2 , ⋯ , y n ] T 其中 y i = m a x ( z i 1 , z i 2 , ⋯ , z i m ) Y=\begin{bmatrix}y_1,y_2,\cdots,y_n\end{bmatrix}^T\quad\text{其中}\quad y_i=max\begin{pmatrix}z_{i1},z_{i2},\cdots,z_{im}\end{pmatrix} Y=[y1,y2,⋯,yn]T其中yi=max(zi1,zi2,⋯,zim)候选人 Y 颜值 牌气(争吵次数) 身高 体重 A 1.17 1.17 0.00 0.00 0.00 B 2.45 1.04 0.90 2.45 1.00 C 2.10 0.78 2.10 0.55 2.00 -
计算关联系数
记差值矩阵为 K K K
K n m = [ k 11 k 12 ⋯ k 1 m k 21 k 22 ⋯ k 2 m ⋮ ⋮ ⋱ ⋮ k n 1 k n 2 ⋯ k n m ] = [ ∣ z 11 − y 11 ∣ ∣ z 2 − y 1 ∣ ⋯ ∣ z 1 m − y 1 ∣ ∣ z 21 − y 2 ∣ ∣ z 22 − y 2 ∣ ⋯ ∣ z 2 m − y 2 ∣ ⋮ ⋮ ⋱ ⋮ ∣ z n 1 − y n ∣ ∣ z n 2 − y n ∣ ⋯ ∣ z n m − y n ∣ ] a = min i min k ∣ x o ( k ) − x i ( k ) ∣ b = max i max k ∣ x o ( k ) − x i ( k ) ∣ \begin{aligned}&K_{nm}=\begin{bmatrix}k_{11}&k_{12}&\cdots&k_{1m}\\k_{21}&k_{22}&\cdots&k_{2m}\\\vdots&\vdots&\ddots&\vdots\\k_{n1}&k_{n2}&\cdots&k_{nm}\end{bmatrix}=\begin{bmatrix}\left|z_{11}-y_{11}\right|&\left|z_{2}-y_{1}\right|&\cdots&\left|z_{1m}-y_{1}\right|\\\left|z_{21}-y_{2}\right|&\left|z_{22}-y_{2}\right|&\cdots&\left|z_{2m}-y_{2}\right|\\\vdots&\vdots&\ddots&\vdots\\\left|z_{n1}-y_{n}\right|&\left|z_{n2}-y_{n}\right|&\cdots&\left|z_{nm}-y_{n}\right|\end{bmatrix}\\&a=\min_{i}\min_{k}\left|x_{o}\left(k\right)-x_{i}\left(k\right)\right|b=\max_{i}\max_{k}\left|x_{o}\left(k\right)-x_{i}\left(k\right)\right|\end{aligned} Knm=⎣⎢⎢⎢⎡k11k21⋮kn1k12k22⋮kn2⋯⋯⋱⋯k1mk2m⋮knm⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡∣z11−y11∣∣z21−y2∣⋮∣zn1−yn∣∣z2−y1∣∣z22−y2∣⋮∣zn2−yn∣⋯⋯⋱⋯∣z1m−y1∣∣z2m−y2∣⋮∣znm−yn∣⎦⎥⎥⎥⎤a=iminkmin∣xo(k)−xi(k)∣b=imaxkmax∣xo(k)−xi(k)∣候选人 Y Y Y Z 1 Z_1 Z1 Z 2 Z_2 Z2 Z 3 Z_3 Z3 Z 4 Z_4 Z4 ∥ z k 1 − y k ∥ \|z_{k1} - y_k\| ∥zk1−yk∥ ∥ z k 2 − y k ∥ \|z_{k2} - y_k\| ∥zk2−yk∥ ∥ z k 3 − y k ∥ \|z_{k3} - y_k\| ∥zk3−yk∥ ∥ z k 4 − y k ∥ \|z_{k4} - y_k\| ∥zk4−yk∥ A A A 1.17 1.17 0.00 0.00 0.00 0.00 1.17 1.17 1.17 B B B 2.45 1.04 0.90 2.45 1.00 1.41 1.55 0.00 1.45 C C C 2.10 0.78 2.10 0.55 2.00 1.32 0.00 1.55 0.10 易得a=0,b=1.55
ξ i ( k ) = y ( x 0 ( k ) , x i ( k ) ) = 0 + 0.5 × 1.55 ∣ x 0 ( k ) − x i ( k ) ∣ + 0.5 × 1.55 = 0.775 ∣ x 0 ( k ) − x i ( k ) ∣ + 0.775 \xi_{i}\left(k\right)=y\left(x_{0}\left(k\right),x_{i}\left(k\right)\right)=\frac{0+0.5\times1.55}{\left|x_{0}\left(k\right)-x_{i}\left(k\right)\right|+0.5\times1.55}=\frac{0.775}{\left|x_{0}\left(k\right)-x_{i}\left(k\right)\right|+0.775} ξi(k)=y(x0(k),xi(k))=∣x0(k)−xi(k)∣+0.5×1.550+0.5×1.55=∣x0(k)−xi(k)∣+0.7750.775候选人 ∥ z k 1 − y k ∥ \|z_{k1}-y_k\| ∥zk1−yk∥ ∥ z k 2 − y k ∥ \|z_{k2}-y_k\| ∥zk2−yk∥ ∥ z k 3 − y k ∥ \|z_{k3}-y_k\| ∥zk3−yk∥ ∥ z k 4 − y k ∥ \|z_{k4}-y_k\| ∥zk4−yk∥ ξ 1 \xi_1 ξ1 ξ 2 \xi_2 ξ2 ξ 3 \xi_3 ξ3 ξ 4 \xi_4 ξ4 A 0.00 1.17 1.17 1.17 1.000 0.398 0.398 0.398 B 1.41 1.55 0.00 1.45 0.355 0.333 1.000 0.348 C 1.32 0.00 1.55 0.10 0.370 1.000 0.333 0.886 -
计算关联度
r i = 1 n ∑ k = 1 n ξ i ( k ) = 1 n ∑ k = 1 n y ( x 0 ( k ) , x i ( k ) ) r_{i}=\frac{1}{n}\sum_{k=1}^{n}\xi_{i}\left(k\right)=\frac{1}{n}\sum_{k=1}^{n}y\Big(x_{0}\left(k\right),x_{i}\left(k\right)\Big) ri=n1k=1∑nξi(k)=n1k=1∑ny(x0(k),xi(k))候选人 ξ 1 \xi_1 ξ1 ξ 2 \xi_2 ξ2 ξ 3 \xi_3 ξ3 ξ 4 \xi_4 ξ4 A 1.000 0.398 0.398 0.398 B 0.355 0.333 1.000 0.348 C 0.370 1.000 0.333 0.886 r 0.575 0.577 0.577 0.544 -
计算指标权重
将关联度归一化即可得到指标权重
w i = r i ∑ k = 1 m r k ( i = 1 , 2 , ⋯ , m ) \begin{aligned}w_{i}&=\frac{r_{i}}{\sum_{k=1}^{m}r_{k}}\big(i=1,2,\cdots,m\big)\end{aligned} wi=∑k=1mrkri(i=1,2,⋯,m)候选人 颜值 脾气(争吵次数) 身高 体重 r 0.575 0.577 0.577 0.544 W 0.253 0.254 0.254 0.239 -
计算得分并归一化
候选人 颜值 脾气(争吵次数) 身高 体重 得分 归一化得分 A 1.17 0.00 0.00 0.00 0.296 0.099 B 1.04 0.90 2.45 1.00 1.353 0.451 C 0.78 2.10 0.55 2.00 1.348 0.450
因此选择B
4. python代码实现
4.1 关联分析
import numpy as npA = np.array(eval(input("请输入初始矩阵:")))# 求出每一列的均值以供后续的数据处理
Mean = np.mean(A, axis=0)# 预处理后的矩阵
A_norm = A/Meanprint("预处理后的矩阵为:\n", A_norm)# 母序列
Y = A_norm[:, 0]# 子序列
X = A_norm[:, 1:]# 计算|x0-xi|矩阵,这里把x0看作是Y
absX0_Xi = np.abs(X-np.tile(Y.reshape(-1, 1), (1, X.shape[1])))# 计算两级最小差a
a = np.min(absX0_Xi)# 计算两级最大差b
b = np.max(absX0_Xi)# 分布系数取0.5
rho = 0.5# 计算子序列各个指标与母序列的关联系数
gamma = (a+rho*b)/(absX0_Xi+rho*b)print("各个指标与母序列的关联系数为:\n", np.mean(gamma, axis=0))
输入:
[[55,24,10],[65,38,22],[75,40,18],[100,50,20]]
输出:
预处理后的矩阵为:[[0.74576271 0.63157895 0.57142857][0.88135593 1. 1.25714286][1.01694915 1.05263158 1.02857143][1.3559322 1.31578947 1.14285714]]
各个指标与母序列的关联系数为:[0.76966578 0.60058464]
4.2 灰色关联综合评价
import numpy as np# 从用户输入参评数目和指标数目
print("请输入参评数目:")
n = int(input())
print("请输入指标数目:")
m = int(input())# 接受用户输入的类型矩阵
print("请输入类型矩阵:1. 极大型 2. 极小型 3. 中间型 4.区间型")
kind = input().split(" ")# 接受用户输入的矩阵并转化为向量
print("请输入矩阵:")
A = np.zeros(shape=(n, m))
for i in range(n):A[i] = input().split(" ")A[i] = list(map(float, A[i]))
print("输入矩阵为:\n{}".format(A))# 极小型指标转化为极大型指标的函数def minTomax(maxx, x):x = list(x)ans = [[(maxx-e) for e in x]]return np.array(ans)# 中间型指标转化为极大型指标的函数def midTomax(bestx, x):x = list(x)h = [abs(e-bestx) for e in x]M = max(h)if M == 0:M = 1 # 防止最大差值为0的情况ans = [[1-(e/M) for e in h]]return np.array(ans)# 区间型指标转化为极大型指标的函数def regTomax(lowx, highx, x):x = list(x)M = max(lowx-min(x), max(x)-highx)if M == 0:M = 1 # 防止最大差值为0的情况ans = []for i in range(len(x)):if x[i] < lowx:ans.append(1-(lowx-x[i])/M)elif x[i] > highx:ans.append(1-(x[i]-highx)/M)else:ans.append(1)return np.array([ans])# 同一指标类型,将所有指标转化为极大型指标
X = np.zeros(shape=(n, 1))
for i in range(m):if kind[i] == "1":v = np.array(A[:, i])elif kind[i] == "2":maxA = max(A[:, i])v = minTomax(maxA, A[:, i])elif kind[i] == "3":print("类型三,请输入最优值:")bestA = eval(input())v = midTomax(bestA, A[:, i])elif kind[i] == "4":print("类型四,请输入区间[a,b]值a:")lowA = eval(input())print("类型四,请输入区间[a,b]值b:")highA = eval(input())v = regTomax(lowA, highA, A[:, i])if i == 0:X = v.reshape(-1, 1) # 如果是第一个指标,直接赋值else:X = np.hstack((X, v.reshape(-1, 1))) # 如果不是第一个指标,横向拼接
print("统一指标后矩阵为:\n{}".format(X))# 对正向化后的矩阵进行预处理
Mean = np.mean(X, axis=0)
Z = X/Mean
print("预处理后的矩阵为:")
print(Z)# 构造母序列和子序列
Y = np.max(Z, axis=1) # 选取每一行最大值构成列向量的母序列
X = Z# 计算得分
absX0_Xi = np.abs(X-np.tile(Y.reshape(-1, 1), (1, X.shape[1])))
a = np.min(absX0_Xi)
b = np.max(absX0_Xi)# 分辨系数
rho = 0.5
gamma = (a+rho*b)/(absX0_Xi+rho*b) # 计算关联系数
weight = np.mean(gamma, axis=0)/np.sum(np.mean(gamma, axis=0)) # 利用子序列中各个指标与母序列的灰色关联度计算权重
score = np.sum(X*np.tile(weight, (X.shape[0], 1)), axis=1) # 未归一化得分
stand_S = score/np.sum(score) # 归一化得分
sorted_S = np.sort(stand_S)[::-1] # 进行降序排序
index = np.argsort(stand_S)[::-1] # 得到排序后的索引print("归一化后的得分及其索引(降序):")
print(sorted_S)
print(index)
输入:
请输入参评数目:
3
请输入指标数目:
4
请输入类型矩阵:1. 极大型 2. 极小型 3. 中间型 4.区间型
1 2 3 4
请输入矩阵:
9 10 175 120
8 7 164 80
6 3 157 90
输入矩阵为:
[[ 9. 10. 175. 120.][ 8. 7. 164. 80.][ 6. 3. 157. 90.]]
类型三,请输入最优值:165
类型四,请输入区间[a,b]值a:
90
类型四,请输入区间[a,b]值b:
100
输出:
统一指标后矩阵为:
[[9. 0. 0. 0. ][8. 3. 0.9 0.5][6. 7. 0.2 1. ]]
预处理后的矩阵为:
[[1.17391304 0. 0. 0. ][1.04347826 0.9 2.45454545 1. ][0.7826087 2.1 0.54545455 2. ]]
归一化后的得分及其索引(降序):
[0.45160804 0.44937917 0.0990128 ]
[1 2 0]
相关文章:

数学建模笔记—— 灰色关联分析[GRA]
数学建模笔记—— 灰色关联分析[GRA] 灰色关联分析(GRA)1. 相关概念1.1 灰色系统1.2 什么是关联分析?1.3 灰色关联分析 2. 关联分析步骤3. 典型例题3.1 关联分析例题3.2 灰色关联综合评价 4. python代码实现4.1 关联分析4.2 灰色关联综合评价 灰色关联分析(GRA) 1.…...

ICM20948 DMP代码详解(13)
接前一篇文章:ICM20948 DMP代码详解(12) 上一回完成了对inv_icm20948_set_chip_to_body_axis_quaternion函数第2步即inv_rotation_to_quaternion函数的解析。回到inv_icm20948_set_chip_to_body_axis_quaternion中来,继续往下进行…...

【论软件需求获取方法及其应用】
摘要 2023 年 3 月,我所在的公司承接了某油企智慧加油站平台的建设工作。该项目旨在帮助加油站提升运营效率、降低运营成本和提高销售额。我在该项目中担任系统架构设计师,负责整个项目的架构设计工作。 本文以该项目为例,详细论述软件需求获…...

使用ESP8266和OLED屏幕实现一个小型电脑性能监控
前言 最近大扫除,发现自己还有几个ESP8266MCU和一个0.96寸的oled小屏幕。又想起最近一直想要买一个屏幕作为性能监控,随机开始自己diy。 硬件: ESP8266 MUColed小屏幕杜邦线可以传输数据的数据线 环境 Windows系统Qt6Arduino Arduino 库…...
Nexpose v6.6.266 for Linux Windows - 漏洞扫描
Nexpose v6.6.266 for Linux & Windows - 漏洞扫描 Rapid7 Vulnerability Management, release Aug 21, 2024 请访问原文链接:https://sysin.org/blog/nexpose-6/,查看最新版。原创作品,转载请保留出处。 作者主页:sysin.o…...

ess6新特性
1、let、const 块级作用域声明变量和常量 2、箭头函数 不能构建函数 不能new 没.prototype属性 没有this指向 this指向是根据上下文的 往上层查找 没有arguments(参数) 3、模板字符串 ${} 字符串中嵌入表达式 4、解构赋值 5、Promise 处理异步操作的标准机制 6、for of 遍历…...

C语言蓝桥杯:语言基础
竞赛常用库函数 最值查询 min_element和max_element在vector(迭代器的使用) nth_element函数的使用 例题lanqiao OJ 497成绩分析 第一种用min_element和max_element函数的写法 第二种用min和max的写法 二分查找 二分查找只能对数组操作 binary_search函数,用于查找…...

axure之变量
一、设置我们的第一个变量 1、点击axure上方设置一个全局变量a 3 2、加入按钮、文本框元件点击按钮文档框展示变量值。 交互选择【单击时】【设置文本】再点击函数。 点击插入变量和函数直接选择刚刚定义的全局变量,也可以直接手动写入函数(注意写入格式。) 这…...

vue缓存用法
Store 临时缓存 特点:需要定义,有初始值、响应式、全局使用、刷新重置 Pinia官方文档 https://pinia.vuejs.org 创建 store 缓存 示例代码 import {defineStore} from pinia import {store} from //storeexport const useMyStore defineStore({// 定义…...

栈入门,括号匹配问题
利用栈这道题应该很轻松可以解决,下面给出常用的代码: public static boolean isValid(String s) {// 创建一个栈来保存左括号Stack<Character> stack new Stack<>();// 遍历字符串中的每个字符for (char c : s.toCharArray()) {// 如果是…...

Vue入门学习笔记-表单
可以使用v-model 指令在表单控件元素上创建双向数据绑定。 引言: Vue采用了MVVM(Model-View-ViewModel)架构模式,通过指令可以快速实现数据和视图的双向绑定 修改视图层时,模型层也会改变;修改模型层&#…...
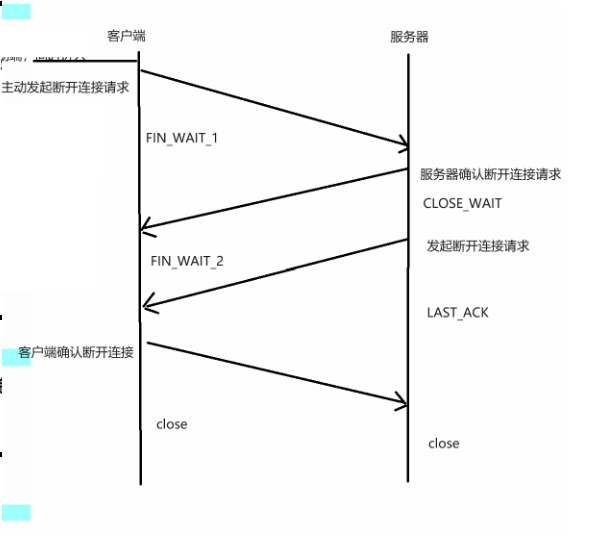
TCP通信三次握手、四次挥手
目录 前言 一、三次握手 TCP三次握手的详细过程 二、四次挥手 四次挥手的详细过程 前言 前面我说到了,UDP通信的实现,但我们经常说UDP通信不可靠,是因为他只会接收和发送,并不会去验证对方收到没有,那么我们说TCP通…...

【实施文档】软件项目实施方案(Doc原件2024实际项目)
软件实施方案 二、 项目介绍 三、 项目实施 四、 项目实施计划 五、 人员培训 六、 项目验收 七、 售后服务 八、 项目保障措施软件开发管理全套资料包清单: 工作安排任务书,可行性分析报告,立项申请审批表,产品需求规格说明书&am…...

BeanFactory vs. ApplicationContext
在Spring框架中,BeanFactory和ApplicationContext都是用于管理Spring容器中的bean的接口,但它们在功能和应用场景上有所不同。下面是它们的主要区别: 1. 基础功能 vs. 扩展功能 BeanFactory: 是Spring框架的最基础的IoC容器,提供…...

JDBC客户端连接Starrocks 2.5
<?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0.0 http://ma…...

004——双向链表和循环链表
目录 双向链表 双向链表的初始化(与单链表类似) 增: Ⅰ)头插法 Ⅱ)尾插法 Ⅲ)中间插入 删 改 查 整体代码示例: 循环链表 循环单链表 编辑 循环双链表 双向链表 不同于单链表&…...

framebuffer帧缓存
framebuffer:帧缓冲,帧缓存 Linux内核为显示提供的一套应用程序接口。(驱动内核支持) framebuffer本质上是一块显示缓存,往显示缓存中写入特定格式的数据就意味着向屏幕输出内容。framebuffer驱动程序控制LCD显示设备࿰…...

24_竞赛中的高效并查集
菜鸟:老鸟,我最近在做一个与社交网络相关的项目,需要频繁地检查两个用户是否属于同一个群组。但我发现每次检查都很耗时,性能很差。你有什么建议吗? 老鸟:你可以试试使用并查集(Union-Find&…...

新手c语言讲解及题目分享(十七)--运算符与表达式专项练习
本文主要讲解c语言的基础部分,运算符与表达式的学习,在这一部分中,往往有许多细节的东西需要去记住。当各种运算符一起用时,就会存在优先级的关系,本文末尾有各种运算符的优先级顺序表。 参考书目和推荐学习书目&#…...

香帅的金融学讲义:深入剖析与解读
香帅的金融学讲义:深入剖析与解读 金融学,这个看似高深复杂的学科,实则与我们的生活息息相关。从个人理财到国家宏观经济政策,金融学无处不在。那么,如何更好地理解金融学呢?今天,我们就来借助…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
