axure之变量
一、设置我们的第一个变量
1、点击axure上方设置一个全局变量a = 3

2、加入按钮、文本框元件点击按钮文档框展示变量值。
交互选择【单击时】【设置文本】再点击函数。

点击插入变量和函数直接选择刚刚定义的全局变量,也可以直接手动写入函数(注意写入格式。)

这样点击按钮时就直接展示刚刚设置的全局变量3了。

2、更改变量值
在新建交互里点击设置变量值。

将a变量设置成等于10.

将新设置的变量值移动到原本的变量值上方,这样在下次调用时方可生效。

二、跨页面调用全局变量
需求:页面A数据用户姓名,用户名输入框命名为【用户名输入框】,页面B提示xx用户注册成功。
这里我们将用户全局变量与局部变量的知识。
页面A先设置好文本框与提交按钮。

页面B展示xx用户已注册成功。

首选我们添加一个全局变量 username,不要给变量值,后续我们通过交互给动态的变量值。

提交按钮设置交互打开【链接】确保点击提交按钮时能跳转到页面B,在交互【设置变量值】这里给的就是动态变量。

目标选择刚刚设置的全局变量名称usernam,设置完后点击函数按钮。

这里我们设置一个局部变量为上方的用户名输入框,上方在应用局部变量名,不然不会生效。

上方的意思就是将当前页面【用户名输入框】的输入信息作为全局变量username的值。

我们再将设置变量值放在打开链接前,这样在页面B引用的时候才会生效。
页面B 提示框的名称为【注册成功提示】
我们在页面B设置载入时设置文本。直接应用username全局变量。

现在就实现了跨页面使用全局变量了。

三、全局变量的运算
现在有这么一个输入框 点击加号时数值+1,点击减号时数值-1,看具体实现方法。
添加一个全局变量value。

页面加入如下元件。点击加号就+1点击减号就-1 中间的命名为【数值】

给加号设置交互【设置变量值】,在原全局变量的基础上+1

再给【数值】设置一个文本。调用刚刚的变量名。

这样就能实现+1,减法也是同理。

相关文章:

axure之变量
一、设置我们的第一个变量 1、点击axure上方设置一个全局变量a 3 2、加入按钮、文本框元件点击按钮文档框展示变量值。 交互选择【单击时】【设置文本】再点击函数。 点击插入变量和函数直接选择刚刚定义的全局变量,也可以直接手动写入函数(注意写入格式。) 这…...

vue缓存用法
Store 临时缓存 特点:需要定义,有初始值、响应式、全局使用、刷新重置 Pinia官方文档 https://pinia.vuejs.org 创建 store 缓存 示例代码 import {defineStore} from pinia import {store} from //storeexport const useMyStore defineStore({// 定义…...

栈入门,括号匹配问题
利用栈这道题应该很轻松可以解决,下面给出常用的代码: public static boolean isValid(String s) {// 创建一个栈来保存左括号Stack<Character> stack new Stack<>();// 遍历字符串中的每个字符for (char c : s.toCharArray()) {// 如果是…...

Vue入门学习笔记-表单
可以使用v-model 指令在表单控件元素上创建双向数据绑定。 引言: Vue采用了MVVM(Model-View-ViewModel)架构模式,通过指令可以快速实现数据和视图的双向绑定 修改视图层时,模型层也会改变;修改模型层&#…...
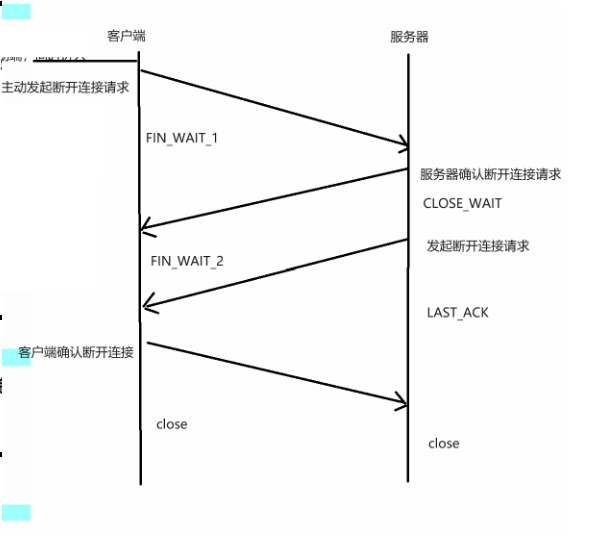
TCP通信三次握手、四次挥手
目录 前言 一、三次握手 TCP三次握手的详细过程 二、四次挥手 四次挥手的详细过程 前言 前面我说到了,UDP通信的实现,但我们经常说UDP通信不可靠,是因为他只会接收和发送,并不会去验证对方收到没有,那么我们说TCP通…...

【实施文档】软件项目实施方案(Doc原件2024实际项目)
软件实施方案 二、 项目介绍 三、 项目实施 四、 项目实施计划 五、 人员培训 六、 项目验收 七、 售后服务 八、 项目保障措施软件开发管理全套资料包清单: 工作安排任务书,可行性分析报告,立项申请审批表,产品需求规格说明书&am…...

BeanFactory vs. ApplicationContext
在Spring框架中,BeanFactory和ApplicationContext都是用于管理Spring容器中的bean的接口,但它们在功能和应用场景上有所不同。下面是它们的主要区别: 1. 基础功能 vs. 扩展功能 BeanFactory: 是Spring框架的最基础的IoC容器,提供…...

JDBC客户端连接Starrocks 2.5
<?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0.0 http://ma…...

004——双向链表和循环链表
目录 双向链表 双向链表的初始化(与单链表类似) 增: Ⅰ)头插法 Ⅱ)尾插法 Ⅲ)中间插入 删 改 查 整体代码示例: 循环链表 循环单链表 编辑 循环双链表 双向链表 不同于单链表&…...

framebuffer帧缓存
framebuffer:帧缓冲,帧缓存 Linux内核为显示提供的一套应用程序接口。(驱动内核支持) framebuffer本质上是一块显示缓存,往显示缓存中写入特定格式的数据就意味着向屏幕输出内容。framebuffer驱动程序控制LCD显示设备࿰…...

24_竞赛中的高效并查集
菜鸟:老鸟,我最近在做一个与社交网络相关的项目,需要频繁地检查两个用户是否属于同一个群组。但我发现每次检查都很耗时,性能很差。你有什么建议吗? 老鸟:你可以试试使用并查集(Union-Find&…...

新手c语言讲解及题目分享(十七)--运算符与表达式专项练习
本文主要讲解c语言的基础部分,运算符与表达式的学习,在这一部分中,往往有许多细节的东西需要去记住。当各种运算符一起用时,就会存在优先级的关系,本文末尾有各种运算符的优先级顺序表。 参考书目和推荐学习书目&#…...

香帅的金融学讲义:深入剖析与解读
香帅的金融学讲义:深入剖析与解读 金融学,这个看似高深复杂的学科,实则与我们的生活息息相关。从个人理财到国家宏观经济政策,金融学无处不在。那么,如何更好地理解金融学呢?今天,我们就来借助…...

java基础-IO(6)转换流InputStreamReader、OutputStreamWriter
引入: 从第一节可知,流分为两类:字节流和字符流,转换流就是在两者之间进行转换。 字节流转换为字符流; 字符流转换为字节流。 字符集 字符集:定义了可用字符及其对应的数字编码的集合。常见的字符集有UT…...

使用Azure Devops Pipeline将Docker应用部署到你的Raspberry Pi上
文章目录 1. 添加树莓派到 Agent Pool1.1 添加pool1.2 添加agent 2. 将树莓派添加到 Deployment Pool2.1 添加pool2.2 添加target 3. 添加编译流水线3.1 添加编译命令3.2 配置触发器 4. 添加发布流水线4.1 添加命令行4.2 配置artifact和触发器 5. 完成 1. 添加树莓派到 Agent P…...

91、K8s之ingress上集
一、Ingress service模式: loadbalance NodePort:每个节点都会有一个指定的端口 30000-32767 内网 clusterip:默认模式,只能pod内部访问 externalName:需要dns提供域名 1.1、对外提供服务的ingress service&…...

NISP 一级 | 2.1 密码学
关注这个证书的其他相关笔记:NISP 一级 —— 考证笔记合集-CSDN博客 通过上一章的学习,我们知道了,网络安全的 CIA 模型,而本期学习的“密码学”,则能为 CIA 模型提供很好的技术支持: 面临的攻击威胁所破坏…...

深度学习速通系列:混淆矩阵是什么
混淆矩阵(Confusion Matrix)是一种评估分类模型性能的工具,尤其在监督学习中用于分析分类结果。它通过一个矩阵的形式,将模型的预测结果与实际标签进行比较,从而可以清晰地看到模型在各个类别上的表现。以下是混淆矩阵…...

综合评价 | 基于熵权-变异系数-博弈组合法的综合评价模型(Matlab)
目录 效果一览基本介绍程序设计参考资料 效果一览 基本介绍 根据信息熵的定义,对于某项指标,可以用熵值来判断某个指标的离散程度,其信息熵值越小,指标的离散程度越大, 该指标对综合评价的影响(即权重&…...
)
模板与泛型编程笔记(一)
1. 推荐书籍 《C新经典 模板与泛型编程》难得的很容易看得懂的好书,作者讲技术不跳跃,娓娓道来,只要花点时间就能看懂。 2. 笔记 模板为什么要用尖括号?因为便于编译器解析,可以将模板和普通函数声明分开。其实尖括…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...

边缘计算网关提升水产养殖尾水处理的远程运维效率
一、项目背景 随着水产养殖行业的快速发展,养殖尾水的处理成为了一个亟待解决的环保问题。传统的尾水处理方式不仅效率低下,而且难以实现精准监控和管理。为了提升尾水处理的效果和效率,同时降低人力成本,某大型水产养殖企业决定…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...

Spring事务传播机制有哪些?
导语: Spring事务传播机制是后端面试中的必考知识点,特别容易出现在“项目细节挖掘”阶段。面试官通过它来判断你是否真正理解事务控制的本质与异常传播机制。本文将从实战与源码角度出发,全面剖析Spring事务传播机制,帮助你答得有…...

前端打包工具简单介绍
前端打包工具简单介绍 一、Webpack 架构与插件机制 1. Webpack 架构核心组成 Entry(入口) 指定应用的起点文件,比如 src/index.js。 Module(模块) Webpack 把项目当作模块图,模块可以是 JS、CSS、图片等…...

短视频时长预估算法调研
weighted LR o d d s T p 1 − p ( 1 − p ) o d d s T p ( T p o d d s ∗ p ) o d d s p o d d s T o d d s odds \frac{Tp}{1-p} \newline (1-p)odds Tp \newline (Tp odds * p) odds \newline p \frac{odds}{T odds} \newline odds1−pTp(1−p)oddsTp(Tpodds…...
