[区间dp]添加括号
题目描述
有一个 n n n 个元素的数组 a a a。不改变序列中每个元素在序列中的位置,把它们相加,并用括号记每次加法所得的和,称为中间和。现在要添上 n − 1 n - 1 n−1 对括号,加法运算依括号顺序进行,得到 n − 1 n - 1 n−1 个中间和,求出使中间和之和最小的添括号方法。
例如:给出序列是 4 , 1 , 2 , 3 4,1,2,3 4,1,2,3 。
第一种添括号方法:
( ( 4 + 1 ) + ( 2 + 3 ) ) = ( ( 5 ) + ( 5 ) ) = ( 10 ) ((4 + 1) + (2 +3)) = ((5) + (5)) = (10) ((4+1)+(2+3))=((5)+(5))=(10)。
有三个中间和是 5 , 5 , 10 5,5,10 5,5,10 ,它们之和为: 5 + 5 + 10 = 20 5 + 5 + 10 = 20 5+5+10=20。
第二种添括号方法:
( 4 + ( ( 1 + 2 ) + 3 ) ) = ( 4 + ( ( 3 ) + 3 ) ) = ( 4 + ( 6 ) ) = ( 10 ) (4 + ((1 + 2) + 3)) = (4 + ((3) + 3)) = (4 + (6)) = (10) (4+((1+2)+3))=(4+((3)+3))=(4+(6))=(10)。
有三个中间和是 3 , 6 , 10 3,6,10 3,6,10 ,它们之和为 3 + 6 + 10 = 19 3 + 6 + 10 = 19 3+6+10=19 。
输入格式
第一行输入一个整数 n n n,表示 a a a 元素个数。
第二行输入 n n n 个整数 a i a_i ai。
输出格式
第一行输出添加括号的方法。
第二行输出最终的中间和之和。
第三行输出 n − 1 n - 1 n−1 个中间和,按照从里到外,从左到右的顺序输出。
样例
样例输入1:
4
4 1 2 3
样例输出1:
(4+((1+2)+3))
19
3 6 10
样例解释见上。
数据范围
1 ≤ n ≤ 20 1 \le n \le 20 1≤n≤20
1 ≤ a i ≤ 100 1 \le a_i \le 100 1≤ai≤100
题解
将 + + + 看成合并左右两个元素, ( ) () () 限定合并顺序。
按照正常的 区间dp ,很容易计算出中间和之和。
那如何输出算式和每个中间和呢?
当把区间 i , k i, k i,k 和 k + 1 , j k + 1, j k+1,j 合并成 i , j i, j i,j 时,记录 k − i k - i k−i 的值(合并位置 d i , j d_{i, j} di,j)。
然后写一个 dfs,传两个参数 l l l 和 r r r,表示 l l l 到 r r r 的区间。
- 如果 l ≥ r l \ge r l≥r,返回。
- 如果 l < r l < r l<r,将 l l l 到 r r r 的区间拆分为两个区间进行
dfs( l l l 到 l + d i , j l + d_{i, j} l+di,j, l + d i , j + 1 l + d_{i, j} + 1 l+di,j+1 到 r r r),并将 l l l 的左括号数( f 1 l f1_l f1l)加 1 1 1, r r r 的右括号数( f 2 r f2_r f2r)加 1 1 1。
接下来从 1 1 1 到 n n n 输出,先输出 f 1 i f1_i f1i 个左括号,再输出 a i a_i ai,然后输出 f 2 i f2_i f2i 个右括号。如果 i ≠ n i \ne n i=n,还要输出 + + +。
这样就能轻松地输出算式了。
输出中间和也是同理,可用前缀和优化。
int f[40][40];//dp
int sum[40];//前缀和
int d[40][40];//从 i 到 j 合并的点
int f1[40], f2[40];//左括号数和右括号数
//算式
void dfs(int x, int y){if(x >= y){return;}dfs(x, x + d[x][y]);dfs(x + d[x][y] + 1, y);f1[x] ++;f2[y] ++;
}
//中间和
void dfs2(int x, int y){if(x >= y){return;}dfs2(x, x + d[x][y]);dfs2(x + d[x][y] + 1, y);printf("%d ", sum[y] - sum[x - 1]);
}
int main(){输入//初始化memset(f, 0x3f, sizeof(f)));memset(d, 0, sizeof(d));for(int i = 1; i <= n; ++ i){f[i][i] = 0;}//前缀和for(int i = 1; i <= n; ++ i){sum[i] = sum[i - 1] + a[i];}for(int k = 1; k < n; ++ k){for(int i = 1; i <= n - k; ++ i){int j = i + k;for(int u = i; u < j; ++ u){//更新 f[i][j]if(f[i][j] > f[i][u] + f[u + 1][j]){f[i][j] = f[i][u] + f[u + 1][j];d[i][j] = u - i;}}f[i][j] += sum[j] - sum[i - 1];}}//输出 dfs(1, n); for(int i = 1; i <= n; ++ i){while(f1[i]){putchar('(');f1[i] --;}printf("%d", a[i]);while(f2[i]){putchar(')');f2[i] --;}if(i != n){putchar('+');}}printf("\n%d\n", f[1][n]);dfs2(1, n);return 0;
}
禁止抄袭!!!
相关文章:

[区间dp]添加括号
题目描述 有一个 n n n 个元素的数组 a a a。不改变序列中每个元素在序列中的位置,把它们相加,并用括号记每次加法所得的和,称为中间和。现在要添上 n − 1 n - 1 n−1 对括号,加法运算依括号顺序进行,得到 n − …...

jenkins流水线+k8s部署springcloud微服务架构项目
文章目录 1.k8s安装2.jenkins安装3.k8s重要知识1.简介2.核心概念3.重要命令1.查看集群消息2.命名空间3.资源创建/更新4.资源查看5.描述某个资源的详细信息6.资源编辑7.资源删除8.资源重启9.查看资源日志10.资源标签 4.k8s控制台1.登录2.界面基本操作1.选择命名空间2.查看命名空…...
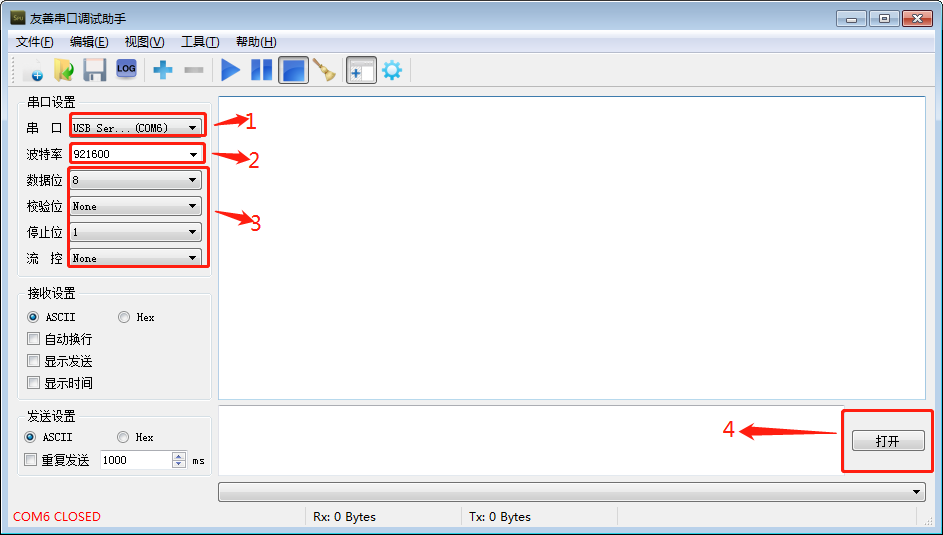
安卓开发板_联发科MTK开发评估套件串口调试
串口调试 如果正在进行lk(little kernel ) 或内核开发,USB 串口适配器( USB 转串口 TTL 适配器的简称)对于检查系统启动日志非常有用,特别是在没有图形桌面显示的情况下。 1.选购适配器 常用的许多 USB 转串口的适配器…...

vue+el-table 可输入表格使用上下键进行input框切换
使用上下键进行完工数量这一列的切换 <el-table :data"form.detailList" selection-change"handleChildSelection" ref"bChangeOrderChild" max-height"500"><!-- <el-table-column type"selection" width&quo…...

中国书法——孙溟㠭浅析碑帖《三希堂法帖》
孙溟㠭浅析碑帖《三希堂法帖》 全称是《三希堂石渠宝笈法帖》,是中国清代宫廷刻帖,一共三十二册。 清朝高宗弘历收藏了晋王羲之《快雪时晴帖》,王献之的《中秋帖》,王珣的《伯远帖》三种王氏原墨迹。故而把所藏法书之所…...
:颠覆传统的AI创作方式)
深入探讨生成对抗网络(GANs):颠覆传统的AI创作方式
在人工智能的快速发展中,生成对抗网络(Generative Adversarial Networks, GANs)无疑是一个引人注目的技术。自2014年由Ian Goodfellow等人首次提出以来,GANs已经在图像生成、文本生成、视频生成等多个领域展现出了惊人的能力。本文…...

vmware Vnet8虚拟网卡丢失的找回问题
vmware Vnet8虚拟网卡丢失的找回问题 1.打开VMware Workstation 2.然后点击Edit --> Virtual Network Edit --> 打开Virtual Network Edit框 , 3.点击最下面的的Restore Default 按钮, 3.恢复默认设置,这会在网络连接那块可以看到丢失…...

Python 从入门到实战13(字符串简介)
我们的目标是:通过这一套资料学习下来,通过熟练掌握python基础,然后结合经典实例、实践相结合,使我们完全掌握python,并做到独立完成项目开发的能力。 上篇文章我们通过举例学习了流程控制语句中的循环语句。今天继续讨…...

Redis_RDB持久化
基于RDB的持久化方式会把当前内存中所有的redis键值对数据以快照的方式写入硬盘文件中,如果需要恢复数据,就把快照文件读到内存中。 RDB快照文件是经压缩的二进制格式的文件,它的储存路径不仅可以在redis服务器启动前通过配置参数来设置&…...

SOP流程制定:vioovi ECRS工时分析软件的智慧引领
在现代制造业中,标准化操作流程(SOP)已成为提升生产效率、确保产品质量、降低运营成本的关键要素。SOP不仅为生产活动提供了明确的指导,还促进了企业管理的规范化和精细化。然而,如何科学、高效地制定SOP流程ÿ…...
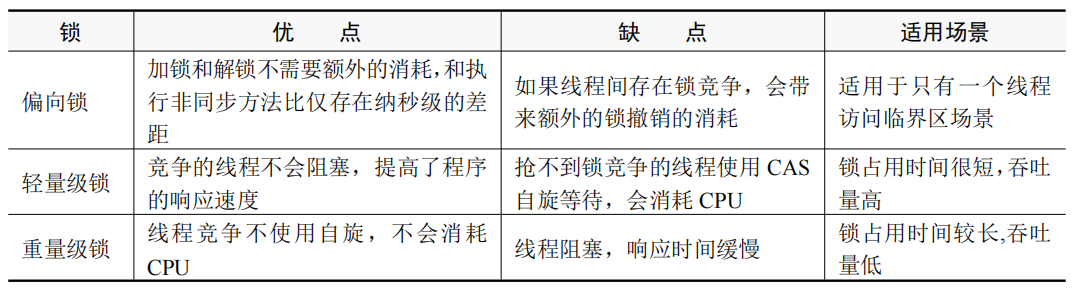
并发编程-synchronized解决原子性问题
并发编程-synchronized解决原子性问题 文章目录 并发编程-synchronized解决原子性问题零、说在前面一、线程安全问题1.1 什么是线程安全问题1.2 自增运算不是线程安全的1.3 临界区资源与临界区代码段 二、synchronized 关键字的使用2.1 synchronized 关键字作用2.2 synchronize…...

CSS之我不会
非常推荐html-css学习视频:尚硅谷html-css 一、选择器 作用:选择页面上的某一个后者某一类元素 基本选择器 1.标签选择器 格式:标签{} <h1>666</h1><style>h1{css语法} </style>2.类选择器 格式:.类…...

AI绘画:SD打光神器!(Stable Diffusion进阶篇:Imposing Consistent Light)
前言 在上一篇笔记中学习了如何简单地下载以及使用IC-Light,今天的内容会稍微有点不一样。 对于学过stable diffusion的小伙伴来说,forge UI和Comfy UI会更加熟悉一些。在IC-Light发布后,Openpose editor的开发者将其制作成了一个Forge UI上…...

QQ频道机器人零基础开发详解(基于QQ官方机器人文档)[第二期]
QQ频道机器人零基础开发详解(基于QQ官方机器人文档)[第二期] 第二期介绍:频道模块之频道管理 目录 QQ频道机器人零基础开发详解(基于QQ官方机器人文档)[第二期]第二期介绍:频道模块之频道管理获取用户详情获取用户频道列表获取频道详情获取子频道列表获…...

参赛心得和思路分享:2021第二届云原生编程挑战赛2: 实现一个柔性集群调度机制
关联比赛: 2021第二届云原生编程挑战赛2:实现一个柔性集群调度机制 参赛心得 历时快两个月的第二届云原生编程挑战赛结束了,作为第一次参赛的萌新,拿下了28名的成绩,与第一名差了19万分,因为赛制时间太长,…...

具体函数的卡诺图填入
目录 用卡诺图表示逻辑函数 基本步骤 例子1 例子2 例子3 用卡诺图表示逻辑函数 基本步骤 例子1 由真值表得卡诺图。 在函数值为1的地方在卡诺图上画上1。 例子2 例子3 非标准与或式,要找到公共部分。 将AB所在的那一行填上1。 将A非D的那个部分也填上1。 再…...
计数型信号量)
STM32 HAL freertos零基础(六)计数型信号量
1、计数型信号量 计数型信号量(Counting Semaphore)是另一种类型的信号量,它可以保持一个大于等于0的整数值,这个值表示可用资源的数量。本质上相当于队列长度大于1得队列。经典问题就是剩余车辆统计,出入车辆,车辆数据可以实时更新。 2、相关API函数 xSemaphoreCreat…...

Dynamics CRM Ribbon Workbench-the solution contains non-entity components
今天在一个低版本的环境里准备用Ribbon Workbench去编辑一个按钮时,遇到了如下错误 一开始没当回事,以为是我的解决方案问题,去检查了下,只有一个组件,并且哪怕我把组件换成了某个实体也不行,尝试了其他任何…...
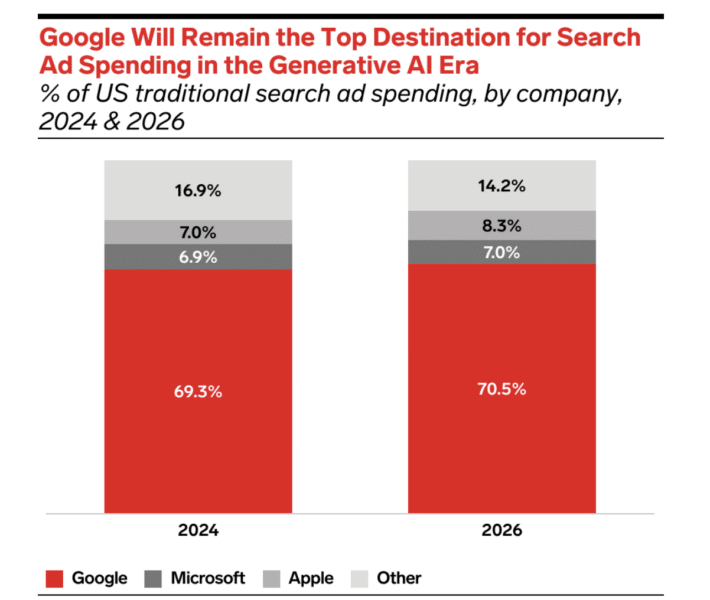
谷歌对抗司法部:为什么谷歌的“数百个竞争对手”说法站不住脚
随着谷歌反垄断陪审团审判的进行,谷歌声称美国司法部对广告技术市场的看法狭隘,并且广告商和出版商有很多替代选择。然而,证据并不支持这一说法。 谷歌误导性地声称有“数百个竞争对手。” 虽然存在许多广告技术提供商,但谷歌在…...

重生奇迹MU 沉迷升级的快感 法魔升级机器人
重生奇迹MU是一款以升级为主要玩法的游戏。升级是游戏基础,也是最重要的部分。通过升级,玩家可以获得更多的基础属性奖励和自由点数奖励,同时还能够穿戴最好的装备和翅膀。因此,升级在游戏中具有极其重要的地位。 史上升级最快的…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
