线性代数 第六讲 特征值和特征向量_相似对角化_实对称矩阵_重点题型总结详细解析
文章目录
- 1.特征值和特征向量
- 1.1 特征值和特征向量的定义
- 1.2 特征值和特征向量的求法
- 1.3 特征值特征向量的主要结论
- 2.相似
- 2.1 相似的定义
- 2.2 相似的性质
- 2.3 相似的结论
- 3.相似对角化
- 4.实对称矩阵
- 4.1 实对称矩阵的基本性质
- 4.2 施密特正交化
- 5.重难点题型总结
- 5.1 判断矩阵能否相似对角化
- 5.2 已知两个矩阵相似,求某个矩阵中的未知参数
- 5.3 相似时,求可逆矩阵P,使得P^-1^AP为对角矩阵
- 5.4 求正交矩阵Q,使Q^T^AQ=Λ
- 5.5 给出条件矩阵A方=A,我们能分析出什么?
- 5.6 已知A为三阶实对称矩阵,三个特征值组成形式为(二重根+单根)和单根特征值的对应的特征向量,求另外两个特征向量
1.特征值和特征向量
1.1 特征值和特征向量的定义
A为n阶,α是n维非0列向量
Aα=λα,α叫A对应λ的特征向量,叫λ特征值
1.2 特征值和特征向量的求法
⭐️三种求法:
- 方法一:利用定义Aα=λα
- 方法二:|λE-A|=0,利用行列式和基础解系
- 方法三:利用相似,P-1AP=B
方法一:
定义法,定义法常常用于A是抽象形式的矩阵,求解其特征值和特征向量的问题。
方法二:
理论基础:
由定义 A α = λ α , α ≠ 0 ⇒ ( λ E − A ) α = 0 , α ≠ 0 ⇒ α 是 ( λ E − A ) x = 0 的非 0 解 由定义A\alpha = \lambda \alpha ,\alpha \neq 0\\\Rightarrow \left(\lambda E - A\right)\alpha = 0,\alpha \neq 0\\\Rightarrow \alpha 是\left(\lambda E - A\right)x = 0的非0解 由定义Aα=λα,α=0⇒(λE−A)α=0,α=0⇒α是(λE−A)x=0的非0解
为什么先用行列式计算特征值,特征向量不能是零向量,所以是非零解,齐次线性方程是非零解,所以行列式=0,所以用行列式计算特征值,再用基础解系计算特征向量。
一.常规计算步骤
特征值的计算步骤:
第一步,计算行列式|λE-A|,因为存在非零解,秩必然是不满的,行列式=0,求出特征值。
第二步,通过求出的特征向量,代入回(λE-A)α=0这个齐次线性方程中,计算出特征向量即齐次线性方程的解向量。
二.通过已积累的结论,直接得出特征值
(1)上下三角矩阵,对角矩阵的特征值就是矩阵主对角线上的元素。
[ 1 2 4 0 3 5 0 0 6 ] , 特征值为 λ 1 = 1 , λ 2 = 3 , λ 3 = 6 \left[\begin{matrix} 1 & 2 & 4 \\ 0 & 3 & 5 \\ 0 & 0 & 6 \\ \end{matrix}\right],特征值为\lambda _{1} = 1,\lambda _{2} = 3,\lambda _{3} = 6 100230456 ,特征值为λ1=1,λ2=3,λ3=6
(2)秩1矩阵,特征值是它的迹,其余都是0
[ a a a a a a a a a ] 特征值为 λ 1 = 3 a , λ 2 = 0 , λ 3 = 0 \left[\begin{matrix} a & a & a \\ a & a & a \\ a & a & a \\ \end{matrix}\right]特征值为\lambda _{1} = 3a,\lambda _{2} = 0,\lambda _{3} = 0 aaaaaaaaa 特征值为λ1=3a,λ2=0,λ3=0
(3)通过已知矩阵A的特征值和特征向量,直接得到关于A矩阵其他基本变形的特征值和特征向量

f(A)多项式与A相似
1.3 特征值特征向量的主要结论
- 如a1a2是矩阵A关于特征值λ的特征向量,则k1a1+k2a2(非0时)仍是A关于λ的的特征向量。若a1a2是不同特征值的特征向量,则k1a1+k2a2不是A关于λ的的特征向量
∣ A ∣ = Π λ i , 其中 Π 是连乘 Σ λ i = Σ a i i = t r ( A ) , 矩阵的迹是特征值的和 \left|A\right| = \Pi \lambda _{i},其中\Pi 是连乘\\\Sigma \lambda _{i} = \Sigma a_{ii} = t_{r}\left(A\right),矩阵的迹是特征值的和 ∣A∣=Πλi,其中Π是连乘Σλi=Σaii=tr(A),矩阵的迹是特征值的和
3.不同特征值的特征向量线性无关
4.λi是属于A的k重特征值,属于λi的k重特征向量最多不超过k个。
2.相似
2.1 相似的定义
相似的定义:
A矩阵相似于B,A~B,意味着存在可逆矩阵P使P-1AP=B
注意注意:A相似于B,这句话是有方向性的,规定是P-1AP=B,而B=PAP-1,A相似于B不能颠倒,没有P-1BP=A这种说法
2.2 相似的性质
A~B,则有以下结论
(1)|A|=|B|
(2)r(A)=r(B)
(3)|λE-A|=|λE-B|,即λA=λB
(4)迹相同,特征值都相同,迹肯定相同
(5)A,B的各阶主子式之和分别相等
关于性质(5)的说明,各阶主子式就是选行和选列的时候,行下标和列下标是一样的,下面给出列子,给出三阶矩阵,求二阶主子式,二阶主子式仅适合用于0多的题
[ 1 2 3 4 5 6 7 8 9 ] ,二阶主子式, [ 1 2 4 5 ] , [ 1 3 4 6 ] , [ 2 3 5 6 ] , [ 4 5 7 8 ] , [ 4 6 7 9 ] , [ 5 6 8 9 ] \left[\begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{matrix}\right],二阶主子式,\left[\begin{matrix} 1 & 2 \\ 4 & 5 \\ \end{matrix}\right],\left[\begin{matrix} 1 & 3 \\ 4 & 6 \\ \end{matrix}\right],\left[\begin{matrix} 2 & 3 \\ 5 & 6 \\ \end{matrix}\right],\left[\begin{matrix} 4 & 5 \\ 7 & 8 \\ \end{matrix}\right],\left[\begin{matrix} 4 & 6 \\ 7 & 9 \\ \end{matrix}\right],\left[\begin{matrix} 5 & 6 \\ 8 & 9 \\ \end{matrix}\right] 147258369 ,二阶主子式,[1425],[1436],[2536],[4758],[4769],[5869]
(6)充要条件 A~B, A+kE~B+kE
2.3 相似的结论
A与B相似的进一步推导结论

矩阵A与B相似
- A-1相似于B-1
- A*相似于B*
- AT相似于BT
- 关于分块矩阵
若 A ~ C , B ~ D , 则 [ A O O B ] ~ [ C O O D ] 若A~C,B~D,则\left[\begin{matrix} A & O \\ O & B \\ \end{matrix}\right]~\left[\begin{matrix} C & O \\ O & D \\ \end{matrix}\right] 若A~C,B~D,则[AOOB]~[COOD]
3.相似对角化
A为n阶矩阵,存在n阶可逆矩阵P,若P-1AP=Λ,则称A可相似对角化,记做A~Λ,称对角矩阵是A的相似标准型。
关于相似对角化的结论总结:

注意充要条件和充分条件
4.实对称矩阵
4.1 实对称矩阵的基本性质
关于实对称矩阵,有更良好的性质,直接就满足可以相似对角化,并且还可以用正交矩阵相似对角化
实对称矩阵AT=A
1.实对称矩阵必与对角矩阵相似(可相似对角化)
2.实对称矩阵特征值不同特征向量相互正交
3.实对称矩阵可用正交矩阵相似对角化
Q-1AQ=QTAQ=Λ
因为QQT=E,.Q-1=QT
4.2 施密特正交化
根据 实对称矩阵的基本性质,不同特征值的特征向量相互正交,所以我们应该使用施密特正交化将相同特征值下的特征向量正交化,最后特征向量都要单位化。
施密特正交化公式:

5.重难点题型总结
5.1 判断矩阵能否相似对角化
例题1:来源 李永乐线代辅导讲义例5.15

例题2:来源 李永乐线代辅导讲义 例5.18

5.2 已知两个矩阵相似,求某个矩阵中的未知参数
解题思路:常常利用两个矩阵相似的性质,若相似矩阵之间的迹相等,行列式相等,各阶主子式之和相等
5.3 相似时,求可逆矩阵P,使得P-1AP为对角矩阵
利用相似的传递性
例题1:来源 李永乐线代辅导讲义例5.20

5.4 求正交矩阵Q,使QTAQ=Λ
例题1:来源 李永乐线代辅导讲义例5.27

5.5 给出条件矩阵A方=A,我们能分析出什么?
有些题目中,给出矩阵A2=A的时候,我们可以得到两方面信息,一方面是关于秩,一方面是关于特征值。
关于秩:
A 2 = A ⇒ A 2 − A = 0 ⇒ A ( A − E ) = 0 ⇒ r ( A ) + r ( A − E ) ≤ n A − ( A − E ) = E ⇒ r ( A ) + r ( B ) ≥ r ( A + B ) ⇒ r ( A ) + r ( A − E ) ≥ r ( E ) = n 综上所述,结论如下: r ( A ) + r ( A − E ) = n A^{2} = A\Rightarrow A^{2} - A = 0\Rightarrow A\left(A - E\right) = 0\Rightarrow r\left(A\right) + r\left(A - E\right) \leq n\\A - \left(A - E\right) = E\Rightarrow r\left(A\right) + r\left(B\right) \geq r\left(A + B\right)\Rightarrow r\left(A\right) + r\left(A - E\right) \geq r\left(E\right) = n\\综上所述,结论如下:r\left(A\right) + r\left(A - E\right) = n A2=A⇒A2−A=0⇒A(A−E)=0⇒r(A)+r(A−E)≤nA−(A−E)=E⇒r(A)+r(B)≥r(A+B)⇒r(A)+r(A−E)≥r(E)=n综上所述,结论如下:r(A)+r(A−E)=n
关于特征值:

5.6 已知A为三阶实对称矩阵,三个特征值组成形式为(二重根+单根)和单根特征值的对应的特征向量,求另外两个特征向量
先不谈这个问题,明确该类问题大方向
首先矩阵一定得是实对称的,因为它的底层原理是实对称向量内积=0
1.假如已知三个特征值,但是它们都是单根,已知一个特征值的特征向量,是无法求出另外两个特征向量的。
2.假如已知A的三个特征值的组成形式是(二重根+单根)和单根特征值的对应的特征向量,求另外两个特征向量,这是可以求出的。
3.假如已知A的三个特征值的组成形式是(二重根+单根)和重根特征值的对应的两个特征向量,求单根的特征向量,也是可以求出的。

相关文章:

线性代数 第六讲 特征值和特征向量_相似对角化_实对称矩阵_重点题型总结详细解析
文章目录 1.特征值和特征向量1.1 特征值和特征向量的定义1.2 特征值和特征向量的求法1.3 特征值特征向量的主要结论 2.相似2.1 相似的定义2.2 相似的性质2.3 相似的结论 3.相似对角化4.实对称矩阵4.1 实对称矩阵的基本性质4.2 施密特正交化 5.重难点题型总结5.1 判断矩阵能否相…...
CSS“多列布局”(补充)——WEB开发系列35
多列布局是一种非常常见的布局方式,适用于内容丰富的页面,如新闻网站、杂志或博客。 一、CSS多列布局概述 CSS多列布局允许我们将内容分成多个垂直列,使页面布局更加灵活和多样化。多列布局的主要属性包括 column-count、column…...

UI自动化测试痛点解决方案
前言 UI自动化测试可以快速、准确地执行大量的测试用例,减少人工测试所需的时间和劳动力。能够在短时间内完成多个测试用例的执行,提高测试的效率和速度。但是UI自动化有个最大的痛点。当前端界面发生变化时,往往页面元素定位也会改变&#…...
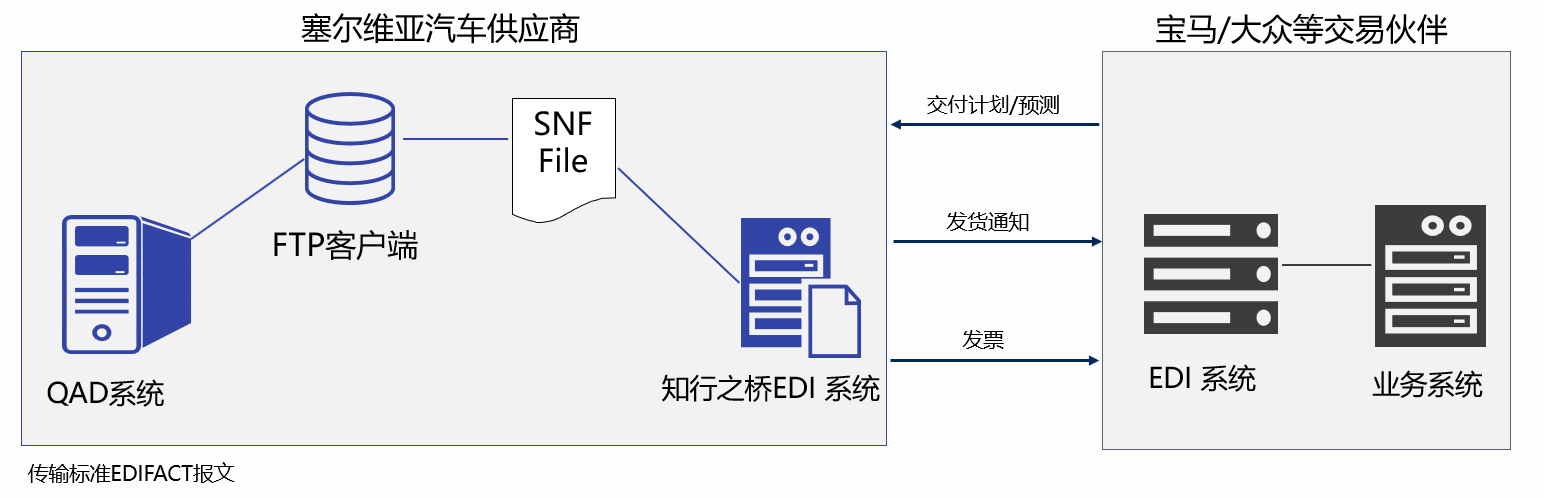
如何将QAD系统EDI模块无缝迁移到知行之桥?
什么是QAD系统? QAD(Quality, Applications, Development)系统,是专为制造业设计的一款ERP软件,主要包含供应链管理、生产管理、财务和客户管理等业务功能,这家公司1979年成立于美国,目前在汽车…...

Linux学习-ELK(一)
配置三台elasticsearch服务器 安装包 elasticsearch.j2 报错 #---执行rsync命令报以下错误 [rootes1 ~]# rsync -av /etc/hosts 192.168.29.172:/etc/hosts root192.168.29.172s password: bash: rsync: 未找到命令 rsync: connection unexpectedly closed (0 bytes receive…...

Selenium事件监听
引言 你一定总是渴望从WebDriver中获得更多的日志信息,以便调试你的脚本或记录更多有关测试的信息。这里为你提供了解决方案:EventFiringWebDriver 和 WebDriverEventListener。EventFiringWebDriver 是一个类,用于包装你的WebDriver以抛出事件,而WebDriverEventListener是…...

视频写作入门:9个步骤开始您的视频日志并与观众建立真实的联系
视频博客(vlogging)通过视频内容帮助你独特的声音和故事被听到,这能与你的观众建立强烈而有意义的联系,从而促进你的业务发展。使用光年AI平台,你可以将业务场景无缝接入AI能力,轻松实现私域流量的增长。 …...

使用豆包MarsCode 编写 Node.js 全栈应用开发实践
以下是「豆包MarsCode 体验官」优秀文章,作者狼叔。 欢迎更多用户使用豆包MarsCode 并分享您的产品使用心得及反馈、创意项目开发等,【有奖征集|人人都是豆包MarsCode 测评官!】活动正在火热进行中,欢迎大家投稿参加&a…...

Spring Cloud全解析:熔断之Hystrix执行流程
Hystrix执行流程 每次调用创建一个新的HystrixCommand,把依赖调用封装在run()方法中执行execute()/queue做同步或异步调用判断熔断器(circuit-breaker)是否打开,如果打开则执行fallback进行降级策略,如果关闭继续执行判断线程池/队列/信号量…...

大模型算法岗,面试百问百答,7天3个offer拿到手!
导读 大模型时代很多企业都在开发自己的大模型,这直接刺激了大模型岗位的需求。本文为大家整理了大模型面试相关的知识点,希望对大家面试求职有所帮助。 今天分享大模型面试相关知识点,持续更新。 1. RAG技术体系的总体思路 数据预处理->…...

代码随想录算法day32 | 动态规划算法part05 | 完全背包,518. 零钱兑换 II, 377. 组合总和 Ⅳ,70. 爬楼梯 (进阶)
完全背包理论基础 本题力扣上没有原题,大家可以去卡码网第52题 (opens new window)去练习,题意是一样的。 完全背包 有N件物品和一个最多能背重量为W的背包。第 i 件物品的重量是 weight[i],得到的价值是 value[i] 。每件物品都有无限个&…...

【Linux 从基础到进阶】自动化备份与恢复策略
自动化备份与恢复策略 在 Linux 运维中,数据的安全性至关重要,自动化备份与恢复策略是保障系统和数据安全的核心环节。无论是系统配置文件、用户数据、数据库还是应用程序日志,备份和恢复都能为系统灾难恢复、数据丢失等突发情况提供可靠的解决方案。 本文将介绍如何在 Ce…...

前端打包装包——设置镜像
1、打包失败,因为没装包,装包失败,因为装包的源错误 npm config get registry npm config set registry https://registry.npmmirror.com/npm install npm run build还是失败,因为缺少了包,在package.json文件中没有包…...

volatile 的作用?是否具有原子性,对编译器有什么影响?什么情况下一定要用 volatile, 能否和 const 一起使用?
目录 1. volatile 的作用 2. 是否具有原子性 3. 对编译器的影响 4.volatile 的使用场景 5.volatile 和 const 的组合 1. volatile 的作用 防止编译器优化:volatile 告诉编译器,变量的值可能会在程序的其他地方(如硬件中断、其他线程等&…...

iPhone 16分辨率,屏幕尺寸,PPI 详细数据对比 iPhone 16 Plus、iPhone 16 Pro、iPhone 16 Pro Max
史上最全iPhone 机型分辨率,屏幕尺寸,PPI详细数据!已更新到iPhone 16系列! 点击放大查看高清图 !...

FunASR搭建语音识别服务和VAD检测
搭建ASR语音识别服务(含VAD检测)教程 在本文中,我将为大家详细介绍如何搭建一套基于FunASR的ASR(语音识别)服务,并集成VAD(语音活动检测)。该服务使用阿里达摩院的模型,…...

设计一个支持多线程写入的并发日志记录系统:C++实战指南
设计一个支持多线程写入的并发日志记录系统:C实战指南 在现代软件开发中,日志记录是一个至关重要的功能,它帮助开发者调试、监控和维护系统。然而,在多线程环境中,日志记录系统需要处理多个线程同时写入日志的问题&am…...

使用LSTM(长短期记忆网络)模型预测股票价格的实例分析
一:LSTM与RNN的区别 LSTM(Long Short-Term Memory)是一种特殊的循环神经网络(RNN)架构。LSTM是为了解决传统RNN在处理长序列数据时遇到的梯度消失或梯度爆炸问题而设计的。 在传统的RNN中,信息通过隐藏状…...

开源的 Windows 12 网页体验版!精美的 UI 设计、丰富流畅的动画
大家周二好呀!博主今天给小伙伴们分享一款炫酷的 Windows 12 体验版,网页效果拉满,非常值得我们去尝试! 如果你对未来的Windows操作系统充满期待,那么这款开源的Windows 12 网页体验版绝对不容错过!这不仅…...

chapter14-集合——(List)——day18
目录 518-Set接口方法 518-Set接口方法...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...
