代码随想录算法day32 | 动态规划算法part05 | 完全背包,518. 零钱兑换 II, 377. 组合总和 Ⅳ,70. 爬楼梯 (进阶)
完全背包理论基础
本题力扣上没有原题,大家可以去卡码网第52题 (opens new window)去练习,题意是一样的。
完全背包
有N件物品和一个最多能背重量为W的背包。第 i 件物品的重量是 weight[i],得到的价值是 value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
leetcode上没有纯完全背包问题,都是需要完全背包的各种应用,需要转化成完全背包问题,所以这里还是以纯完全背包问题进行讲解理论和原理。
在下面的讲解中,都应用于这个例子:
背包最大重量为4。
物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
每件商品都有无限个!
问背包能背的物品最大价值是多少?
01背包和完全背包唯一不同就是体现在遍历顺序上,所以本文就不去做动规五部曲了,我们直接针对遍历顺序经行分析!
首先再回顾一下01背包的核心代码
for(int i = 0; i < weight.length; i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
我们知道01背包内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。
而完全背包的物品是可以添加多次的,所以要从小到大去遍历,即:
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.length; i++) { // 遍历物品for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
dp状态图如下:
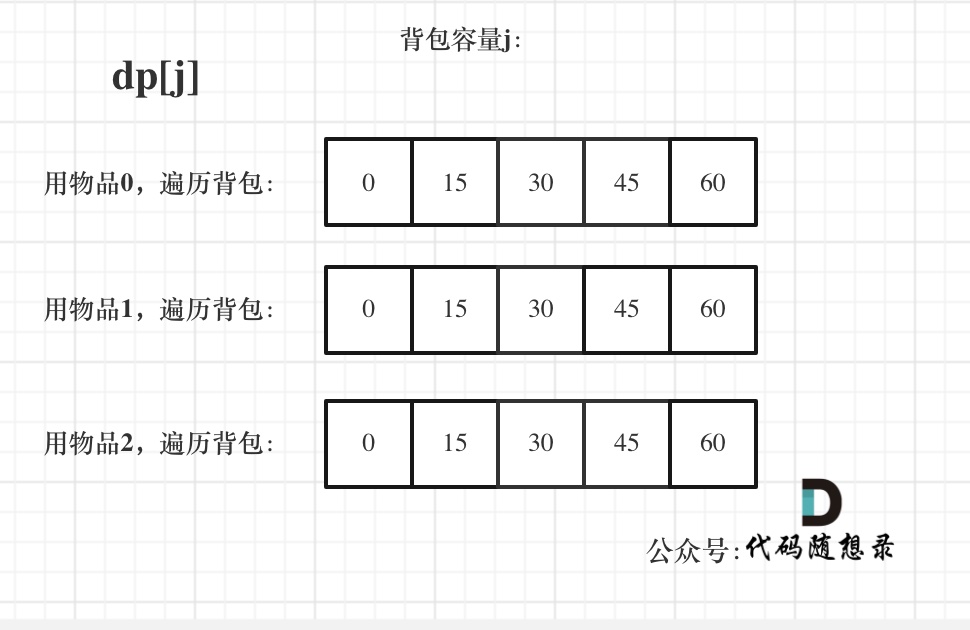
相信很多网上的文章,关于完全背包介绍基本就到为止了。
其实还有一个很重要的问题,为什么遍历物品在外层循环,遍历背包容量在内层循环?
这个问题很多题解关于这里都是轻描淡写就略过了,大家都默认 遍历物品在外层,遍历背包容量在内层,好像本应该如此一样,那么为什么呢?
难道就不能遍历背包容量在外层,遍历物品在内层?
我们之前讲过01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了,一维dp数组的两个for循环先后循序一定是先遍历物品,再遍历背包容量。
在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序是无所谓的!
因为 dp[j] 是根据 下标 j 之前所对应的 dp[j] 计算出来的。 只要保证下标 j 之前的 dp[j] 都是经过计算的就可以了。
遍历物品在外层循环,遍历背包容量在内层循环,状态如图:
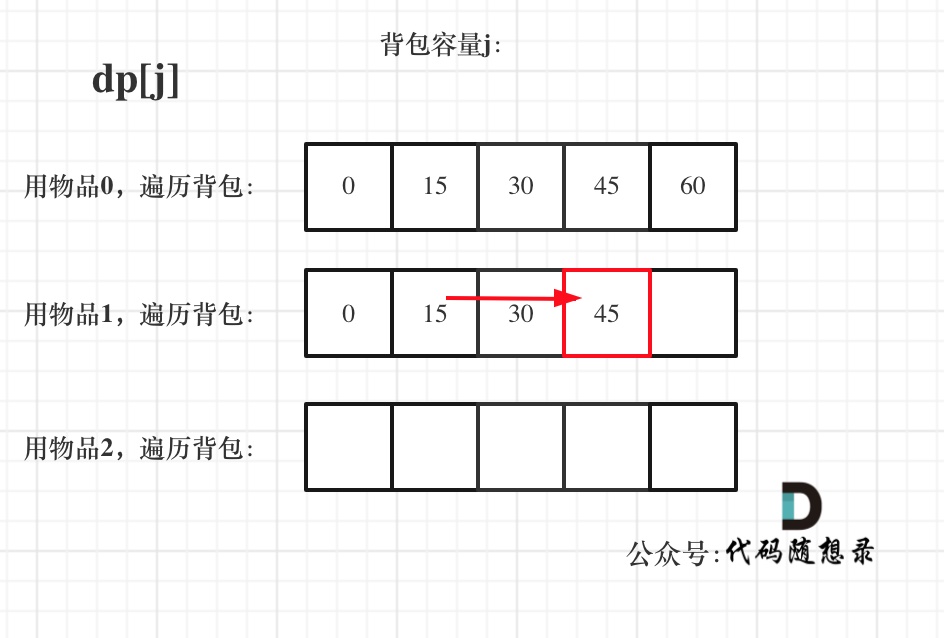
遍历背包容量在外层循环,遍历物品在内层循环,状态如图:
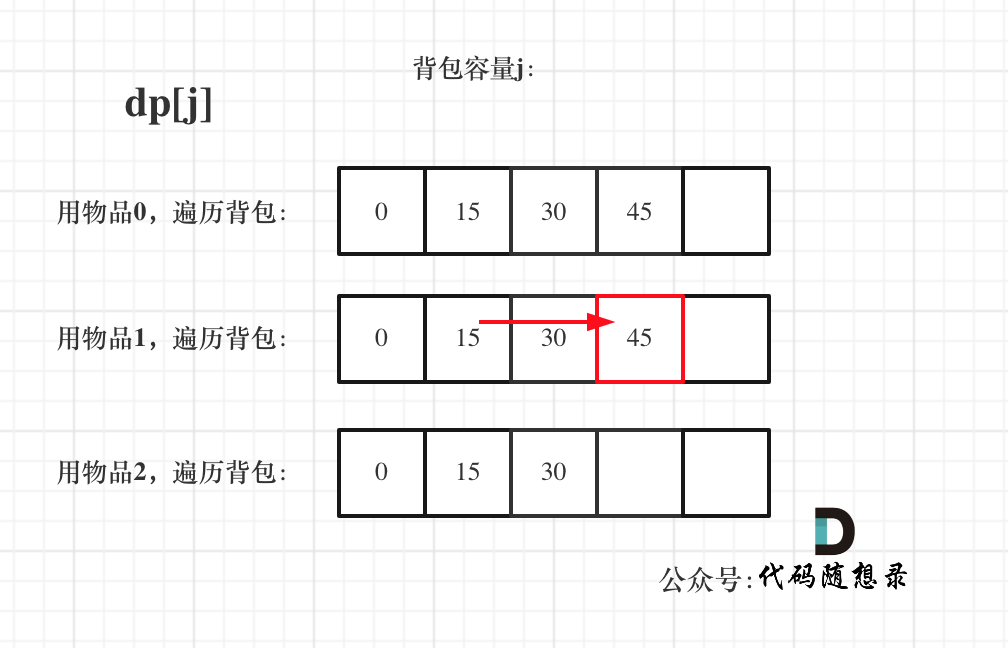
看了这两个图,大家就会理解,完全背包中,两个for循环的先后循序,都不影响计算 dp[j] 所需要的值(这个值就是下标 j 之前所对应的 dp[j])。
先遍历背包在遍历物品,代码如下:
// 先遍历背包,再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量for(int i = 0; i < weight.length; i++) { // 遍历物品if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
完整的Java代码如下:
//先遍历物品,再遍历背包
private static void testCompletePack(){int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWeight = 4;int[] dp = new int[bagWeight + 1];for (int i = 0; i < weight.length; i++){ // 遍历物品for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);}}for (int maxValue : dp){System.out.println(maxValue + " ");}
}//先遍历背包,再遍历物品
private static void testCompletePackAnotherWay(){int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWeight = 4;int[] dp = new int[bagWeight + 1];for (int i = 1; i <= bagWeight; i++){ // 遍历背包容量for (int j = 0; j < weight.length; j++){ // 遍历物品if (i - weight[j] >= 0){dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);}}}for (int maxValue : dp){System.out.println(maxValue + " ");}
}总结
细心的同学可能发现,我说的都是对于纯完全背包问题,其for循环的先后循环是可以颠倒的!
但如果题目稍稍有点变化,就会体现在遍历顺序上。
如果问装满背包有几种方式的话? 那么两个for循环的先后顺序就有很大区别了,而leetcode上的题目都是这种稍有变化的类型。
这里又可以出一道面试题了,就是纯完全背包,要求先用二维dp数组实现,然后再用一维dp数组实现,最后再问,两个for循环的先后是否可以颠倒?为什么? 这个简单的完全背包问题,估计就可以难住不少候选人了。
518.零钱兑换II
力扣题目链接(opens new window)
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
示例 1:
- 输入: amount = 5, coins = [1, 2, 5]
- 输出: 4
解释: 有四种方式可以凑成总金额:
- 5=5
- 5=2+2+1
- 5=2+1+1+1
- 5=1+1+1+1+1
示例 2:
- 输入: amount = 3, coins = [2]
- 输出: 0
- 解释: 只用面额2的硬币不能凑成总金额3。
示例 3:
- 输入: amount = 10, coins = [10]
- 输出: 1
注意,你可以假设:
- 0 <= amount (总金额) <= 5000
- 1 <= coin (硬币面额) <= 5000
- 硬币种类不超过 500 种
- 结果符合 32 位符号整数
这是一道典型的背包问题,一看到钱币数量不限,就知道这是一个完全背包。
但本题和纯完全背包不一样,纯完全背包是凑成背包最大价值是多少,而本题是要求凑成总金额的物品组合个数!
注意题目描述中是凑成总金额的硬币组合数,为什么强调是组合数呢?
例如示例一:
5 = 2 + 2 + 1
5 = 2 + 1 + 2
这是一种组合,都是 2 2 1。
如果问的是排列数,那么上面就是两种排列了。
组合不强调元素之间的顺序,排列强调元素之间的顺序。 其实这一点我们在讲解回溯算法的时候就讲过了哈。
那为什么要讲这些呢,因为这和下文讲解遍历顺序息息相关!
回归本题,动规五步曲来分析如下:
-
确定dp数组以及下标的含义
dp[j]:凑成总金额j的货币组合数为 dp[j]
-
确定递推公式
dp[j] 就是所有的 dp[j - coins[i]](考虑coins[i]的情况)相加。
所以递推公式:dp[j] += dp[j - coins[i]];
这个递推公式大家应该不陌生了,我在讲解01背包题目的时候在这篇 494.目标和 中就讲解了,求装满背包有几种方法,公式都是:dp[j] += dp[j - nums[i]];
-
dp数组如何初始化
首先dp[0]一定要为1,dp[0] = 1是 递归公式的基础。如果dp[0] = 0 的话,后面所有推导出来的值都是0了。
那么 dp[0] = 1 有没有含义,其实既可以说 凑成总金额0的货币组合数为1,也可以说 凑成总金额0的货币组合数为0,好像都没有毛病。
但题目描述中,也没明确说 amount = 0 的情况,结果应该是多少。
这里我认为题目描述还是要说明一下,因为后台测试数据是默认,amount = 0 的情况,组合数为1的。
下标非0的 dp[j] 初始化为0,这样累计加 dp[j - coins[i]] 的时候才不会影响真正的dp[j]
dp[0]=1还说明了一种情况:如果正好选了 coins[i] 后,也就是j-coins[i] == 0的情况表示这个硬币刚好能选,此时dp[0]为1表示只选coins[i]存在这样的一种选法。
-
确定遍历顺序
本题中我们是外层for循环遍历物品(钱币),内层for遍历背包(金钱总额),还是外层for遍历背包(金钱总额),内层for循环遍历物品(钱币)呢?
我在 上题 中讲解了完全背包的两个for循环的先后顺序都是可以的。
但本题就不行了!
因为纯完全背包求得装满背包的最大价值是多少,和凑成总和的元素有没有顺序没关系,即:有顺序也行,没有顺序也行!
而本题要求凑成总和的组合数,元素之间明确要求没有顺序。
所以纯完全背包是能凑成总和就行,不用管怎么凑的。
本题是求凑出来的方案个数,且每个方案个数是为组合数。
那么本题,两个for循环的先后顺序可就有说法了。
我们先来看 外层for循环遍历物品(钱币),内层for遍历背包(金钱总额)的情况。
代码如下:
for (int i = 0; i < coins.length; i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量dp[j] += dp[j - coins[i]];}
}
假设:coins[0] = 1,coins[1] = 5。
那么就是先把1加入计算,然后再把5加入计算,得到的方法数量只有{1, 5}这种情况。而不会出现{5, 1}的情况。
所以这种遍历顺序中dp[j]里计算的是组合数!
如果把两个for交换顺序,代码如下:
for (int j = 0; j <= amount; j++) { // 遍历背包容量for (int i = 0; i < coins.length; i++) { // 遍历物品if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];}
}
背包容量的每一个值,都是经过 1 和 5 的计算,包含了{1, 5} 和 {5, 1}两种情况。
此时dp[j]里算出来的就是排列数!
可能这里很多同学还不是很理解,建议动手把这两种方案的dp数组数值变化打印出来,对比看一看!(实践出真知)
-
举例推导dp数组
输入: amount = 5, coins = [1, 2, 5] ,dp状态图如下:

最后红色框dp[amount]为最终结果。
以上分析完毕,C++代码如下:
class Solution {public int change(int amount, int[] coins) {//递推表达式int[] dp = new int[amount + 1];//初始化dp数组,表示金额为0时只有一种情况,也就是什么都不装dp[0] = 1;for (int i = 0; i < coins.length; i++) {for (int j = coins[i]; j <= amount; j++) {dp[j] += dp[j - coins[i]];}}return dp[amount];}
}- 时间复杂度: O(mn),其中 m 是amount,n 是 coins 的长度
- 空间复杂度: O(m)
是不是发现代码如此精简
总结
本题的递推公式,其实我们在 494.目标和 中就已经讲过了,而难点在于遍历顺序!
在求装满背包有几种方案的时候,认清遍历顺序是非常关键的。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
377. 组合总和 Ⅳ
力扣题目链接(opens new window)
给定一个由正整数组成且不存在重复数字的数组,找出和为给定目标正整数的组合的个数。
示例:
- nums = [1, 2, 3]
- target = 4
所有可能的组合为: (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1)
请注意,顺序不同的序列被视作不同的组合。
因此输出为 7。
本题题目描述说是求组合,但又说是可以元素相同顺序不同的组合算两个组合,其实就是求排列!
弄清什么是组合,什么是排列很重要。
组合不强调顺序,(1,5)和(5,1)是同一个组合。
排列强调顺序,(1,5)和(5,1)是两个不同的排列。
本题的本质求的是排列总和,而且仅仅是求排列总和的个数,并不是把所有的排列都列出来。
如果本题要把排列都列出来的话,只能使用回溯算法爆搜。
动规五部曲分析如下:
-
确定dp数组以及下标的含义
dp[i]: 凑成目标正整数为i的排列个数为dp[i]
-
确定递推公式
dp[i](考虑nums[j])可以由 dp[i - nums[j]](不考虑nums[j]) 推导出来。
因为只要得到nums[j],排列个数dp[i - nums[j]],就是dp[i]的一部分。
我们已经讲过了,求装满背包有几种方法,递推公式一般都是dp[i] += dp[i - nums[j]];
本题也一样。
-
dp数组如何初始化
因为递推公式 dp[i] += dp[i - nums[j]] 的缘故,dp[0] 要初始化为 1,这样递归其他 dp[i] 的时候才会有数值基础。
至于dp[0] = 1 有没有意义呢?
其实没有意义,所以我也不去强行解释它的意义了,因为题目中也说了:给定目标值是正整数! 所以dp[0] = 1是没有意义的,仅仅是为了推导递推公式。
至于非0下标的dp[i]应该初始为多少呢?
初始化为0,这样才不会影响dp[i]累加所有的dp[i - nums[j]]。
-
确定遍历顺序
个数可以不限使用,说明这是一个完全背包。
得到的集合是排列,说明需要考虑元素之间的顺序。
本题要求的是排列,那么这个for循环嵌套的顺序可以有说法了。
在 上题 中就已经讲过了。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
如果把遍历nums(物品)放在外循环,遍历target的作为内循环的话,举一个例子:计算dp[4]的时候,结果集只有 {1,3} 这样的集合,不会有{3,1}这样的集合,因为nums遍历放在外层,3只能出现在1后面!
所以本题遍历顺序最终遍历顺序:target(背包)放在外循环,将nums(物品)放在内循环,内循环从前到后遍历。
-
举例来推导dp数组
我们再来用示例中的例子推导一下:

以上分析完毕,Java代码如下:
class Solution {public int combinationSum4(int[] nums, int target) {int[] dp = new int[target + 1];dp[0] = 1;for (int i = 0; i <= target; i++) {for (int j = 0; j < nums.length; j++) {if (i >= nums[j]) {dp[i] += dp[i - nums[j]];}}}return dp[target];}
}- 时间复杂度: O(target * n),其中 n 为 nums 的长度
- 空间复杂度: O(target)
总结
求装满背包有几种方法,递归公式都是一样的,没有什么差别,但关键在于遍历顺序!
本题与 518.零钱兑换Ⅱ 就是一个鲜明的对比,一个是求排列,一个是求组合,遍历顺序完全不同。
如果对遍历顺序没有深度理解的话,做这种完全背包的题目会很懵逼,即使题目刷过了可能也不太清楚具体是怎么过的。
70. 爬楼梯(进阶版)
卡码网:57. 爬楼梯(opens new window)
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬至多m (1 <= m < n)个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
输入描述:输入共一行,包含两个正整数,分别表示n, m
输出描述:输出一个整数,表示爬到楼顶的方法数。
输入示例:3 2
输出示例:3
提示:
当 m = 2,n = 3 时,n = 3 这表示一共有三个台阶,m = 2 代表你每次可以爬一个台阶或者两个台阶。
此时你有三种方法可以爬到楼顶。
- 1 阶 + 1 阶 + 1 阶段
- 1 阶 + 2 阶
- 2 阶 + 1 阶
之前讲这道题目的时候,因为还没有讲背包问题,所以就只是讲了一下爬楼梯最直接的动规方法(斐波那契)。
这次终于讲到了背包问题,再爬一次楼梯!
这道题目 我们在 爬楼梯 中已经讲过一次了,这次我又给本题加点料,力扣上没有原题,所以可以在卡码网57. 爬楼梯 (opens new window)上来刷这道题目。
我们之前做的 爬楼梯 是只能至多爬两个台阶。
这次改为:一步一个台阶,两个台阶,三个台阶,.......,直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢?
这又有难度了,这其实是一个完全背包问题。
1阶,2阶,.... m阶就是物品,楼顶就是背包。
每一阶可以重复使用,例如跳了1阶,还可以继续跳1阶。
问跳到楼顶有几种方法其实就是问装满背包有几种方法。
此时大家应该发现这就是一个完全背包问题了!
和 377.组合总和Ⅳ 基本就是一道题了。
动规五部曲分析如下:
-
确定dp数组以及下标的含义
dp[i]:爬到有 i 个台阶的楼顶,有 dp[i] 种方法。
-
确定递推公式
求装满背包有几种方法,递推公式一般都是dp[i] += dp[i - nums[j]];
本题呢,dp[i]有几种来源,dp[i - 1],dp[i - 2],dp[i - 3] 等等,即:dp[i - j]
那么递推公式为:dp[i] += dp[i - j];
-
dp数组如何初始化
既然递归公式是 dp[i] += dp[i - j],那么dp[0] 一定为1,dp[0]是递归中一切数值的基础所在,如果dp[0]是0的话,其他数值都是0了。
下标非0的dp[i]初始化为0,因为dp[i]是靠dp[i-j]累计上来的,dp[i]本身为0这样才不会影响结果
-
确定遍历顺序
这是背包里求排列问题,即:1、2 步 和 2、1 步都是上三个台阶,但是这两种方法不一样!
所以需将 target 放在外循环,将 nums 放在内循环。
每一步可以走多次,这是完全背包,内循环需要从前向后遍历。
-
举例来推导dp数组
介于本题和 377.组合总和Ⅳ 几乎是一样的,这里就不再重复举例了。
Java代码如下:
import java.util.Scanner;
class climbStairs{public static void main(String [] args){Scanner sc = new Scanner(System.in);int m, n;while (sc.hasNextInt()) {// 从键盘输入参数,中间用空格隔开n = sc.nextInt();m = sc.nextInt();// 求排列问题,先遍历背包再遍历物品int[] dp = new int[n + 1];dp[0] = 1;for (int j = 1; j <= n; j++) {for (int i = 1; i <= m; i++) {if (j - i >= 0) dp[j] += dp[j - i];}}System.out.println(dp[n]);}}
}- 时间复杂度: O(n * m)
- 空间复杂度: O(n)
总结
本题看起来是一道简单题目,稍稍进阶一下其实就是一个完全背包!
面试题:会先给候选人出一个 本题原题,看其表现,如果顺利写出来,进而在要求每次可以爬[1 - m]个台阶应该怎么写。
顺便再考察一下两个for循环的嵌套顺序,为什么target放外面,nums放里面。
这就能考察对背包问题本质的掌握程度,候选人是不是刷题背公式,一眼就看出来了。
这么一连套下来,如果候选人都能答出来,相信任何一位面试官都是非常满意的。
本题代码不长,题目也很普通,但稍稍一进阶就可以考察完全背包,而且题目进阶的内容在leetcode上并没有原题,一定程度上就可以排除掉刷题党了,简直是面试题目的绝佳选择!
相关文章:

代码随想录算法day32 | 动态规划算法part05 | 完全背包,518. 零钱兑换 II, 377. 组合总和 Ⅳ,70. 爬楼梯 (进阶)
完全背包理论基础 本题力扣上没有原题,大家可以去卡码网第52题 (opens new window)去练习,题意是一样的。 完全背包 有N件物品和一个最多能背重量为W的背包。第 i 件物品的重量是 weight[i],得到的价值是 value[i] 。每件物品都有无限个&…...

【Linux 从基础到进阶】自动化备份与恢复策略
自动化备份与恢复策略 在 Linux 运维中,数据的安全性至关重要,自动化备份与恢复策略是保障系统和数据安全的核心环节。无论是系统配置文件、用户数据、数据库还是应用程序日志,备份和恢复都能为系统灾难恢复、数据丢失等突发情况提供可靠的解决方案。 本文将介绍如何在 Ce…...

前端打包装包——设置镜像
1、打包失败,因为没装包,装包失败,因为装包的源错误 npm config get registry npm config set registry https://registry.npmmirror.com/npm install npm run build还是失败,因为缺少了包,在package.json文件中没有包…...

volatile 的作用?是否具有原子性,对编译器有什么影响?什么情况下一定要用 volatile, 能否和 const 一起使用?
目录 1. volatile 的作用 2. 是否具有原子性 3. 对编译器的影响 4.volatile 的使用场景 5.volatile 和 const 的组合 1. volatile 的作用 防止编译器优化:volatile 告诉编译器,变量的值可能会在程序的其他地方(如硬件中断、其他线程等&…...

iPhone 16分辨率,屏幕尺寸,PPI 详细数据对比 iPhone 16 Plus、iPhone 16 Pro、iPhone 16 Pro Max
史上最全iPhone 机型分辨率,屏幕尺寸,PPI详细数据!已更新到iPhone 16系列! 点击放大查看高清图 !...

FunASR搭建语音识别服务和VAD检测
搭建ASR语音识别服务(含VAD检测)教程 在本文中,我将为大家详细介绍如何搭建一套基于FunASR的ASR(语音识别)服务,并集成VAD(语音活动检测)。该服务使用阿里达摩院的模型,…...

设计一个支持多线程写入的并发日志记录系统:C++实战指南
设计一个支持多线程写入的并发日志记录系统:C实战指南 在现代软件开发中,日志记录是一个至关重要的功能,它帮助开发者调试、监控和维护系统。然而,在多线程环境中,日志记录系统需要处理多个线程同时写入日志的问题&am…...

使用LSTM(长短期记忆网络)模型预测股票价格的实例分析
一:LSTM与RNN的区别 LSTM(Long Short-Term Memory)是一种特殊的循环神经网络(RNN)架构。LSTM是为了解决传统RNN在处理长序列数据时遇到的梯度消失或梯度爆炸问题而设计的。 在传统的RNN中,信息通过隐藏状…...

开源的 Windows 12 网页体验版!精美的 UI 设计、丰富流畅的动画
大家周二好呀!博主今天给小伙伴们分享一款炫酷的 Windows 12 体验版,网页效果拉满,非常值得我们去尝试! 如果你对未来的Windows操作系统充满期待,那么这款开源的Windows 12 网页体验版绝对不容错过!这不仅…...

chapter14-集合——(List)——day18
目录 518-Set接口方法 518-Set接口方法...

Frida 脚本抓取 HttpURLConnection 请求和响应
引入 Java 类: 引入 okhttp3.OkHttpClient、okhttp3.OkHttpClient$Builder、okhttp3.Interceptor、okhttp3.ResponseBody 等类。 创建自定义拦截器: 通过 Java.registerClass 创建自定义拦截器 MyInterceptor。拦截器中重写 intercept 方法࿰…...

Java实现建造者模式和源码中的应用
Java实现建造者模式(Builder Pattern) 文章目录 Java实现建造者模式(Builder Pattern)案例:汉堡制作建造者模式的核心角色代码实现:汉堡制作 🍔内部类实现:Step 1:产品类…...

Windows安装docker
Windows有两种虚拟号技术,WLS和Hyper-V,因为我的win10是家庭版,所以只能采用WLS来安装docker。 在Windows 10家庭版中,由于默认不包含Hyper-V功能,因此容器功能也不可用。即使启用了Hyper-V,由于Docker De…...

SprinBoot+Vue校园车辆管理系统的设计与实现
目录 1 项目介绍2 项目截图3 核心代码3.1 Controller3.2 Service3.3 Dao3.4 application.yml3.5 SpringbootApplication3.5 Vue 4 数据库表设计5 文档参考6 计算机毕设选题推荐7 源码获取 1 项目介绍 博主个人介绍:CSDN认证博客专家,CSDN平台Java领域优质…...

【C语言进阶】C语言动态内存管理:深入理解malloc、calloc与realloc
📝个人主页🌹:Eternity._ ⏩收录专栏⏪:C语言 “ 登神长阶 ” 🤡往期回顾🤡:C语言自定义类型 🌹🌹期待您的关注 🌹🌹 ❀C语言动态内存管理 &#…...

Java+控制台 图书管理系统
Java控制台 图书管理系统 一、系统介绍二、功能展示1.用户登陆2.普通用户:图书查询、图书借阅、图书归还 、图书列表3.管理员:图书整理、图书添加、图书删除 四、其它1.其他系统实现 一、系统介绍 系统实现了普通用户:图书查询、图书借阅、图书归还 、图…...

gi清除无用缓存
使用 git pull --rebase 的确会对 Git 仓库的大小产生影响,主要是因为每次重新基于最新的代码进行 rebase,Git 会保存历史提交的变动。即使你的实际代码量不多,Git 依然需要存储所有这些历史变更记录,因此可能会导致仓库的大小逐渐…...

云PLM系统对企业影响有哪些?解析云PLM系统的作用
随着企业数字化转型的加速,云PLM产品生命周期管理系统逐渐成为企业提升竞争力、优化资源配置、加速产品上市的重要工具。云PLM系统通过云计算技术,不仅解决了传统PLM系统面临的高昂部署成本、复杂维护、数据共享效率低等问题,还为企业带来了更…...

四、查找算法
文章目录 一、查找算法介绍二、线性查找算法2.1 顺序查找2.2 二分查找(折半查找)2.3 插值查找2.4 斐波拉契(黄金分割法)查找算法 三、树表的查找3.1 二叉排序树3.1.1 引入3.1.2 基本介绍3.1.3 二叉树的遍历3.1.4 二叉树的删除 3.2…...

果蔬识别系统性能优化之路(三)
目录 前情提要遗留问题 解决方案优化查询速度优化ivf初始化的速度 下一步 前情提要 果蔬识别系统性能优化之路(二) 遗留问题 优化同步速度,目前大约30秒,不是一个生产速度 这次来解决遗留问题 通过console,发现两个…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

[拓扑优化] 1.概述
常见的拓扑优化方法有:均匀化法、变密度法、渐进结构优化法、水平集法、移动可变形组件法等。 常见的数值计算方法有:有限元法、有限差分法、边界元法、离散元法、无网格法、扩展有限元法、等几何分析等。 将上述数值计算方法与拓扑优化方法结合&#…...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...

Docker、Wsl 打包迁移环境
电脑需要开启wsl2 可以使用wsl -v 查看当前的版本 wsl -v WSL 版本: 2.2.4.0 内核版本: 5.15.153.1-2 WSLg 版本: 1.0.61 MSRDC 版本: 1.2.5326 Direct3D 版本: 1.611.1-81528511 DXCore 版本: 10.0.2609…...
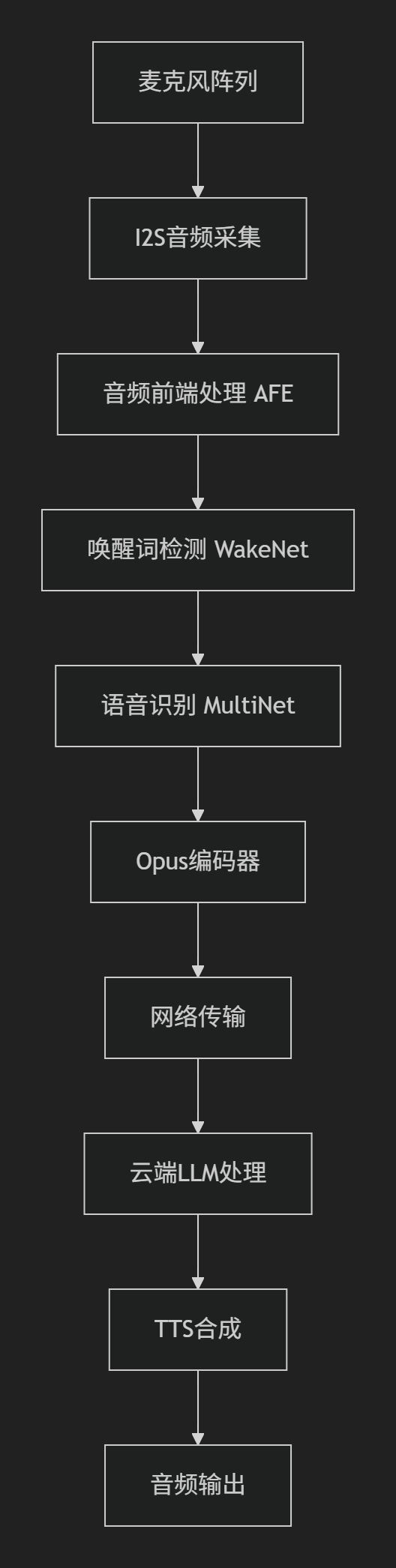
SDU棋界精灵——硬件程序ESP32实现opus编码
一、 音频处理框架 该项目基于Espressif的音频处理框架构建,核心组件包括 ESP-ADF 和 ESP-SR,以下是完整的音频处理框架实现细节: 1.核心组件 (1) 音频前端处理 (AFE - Audio Front-End) main/components/audio_pipeline/afe_processor.c功能: 声学回声…...
